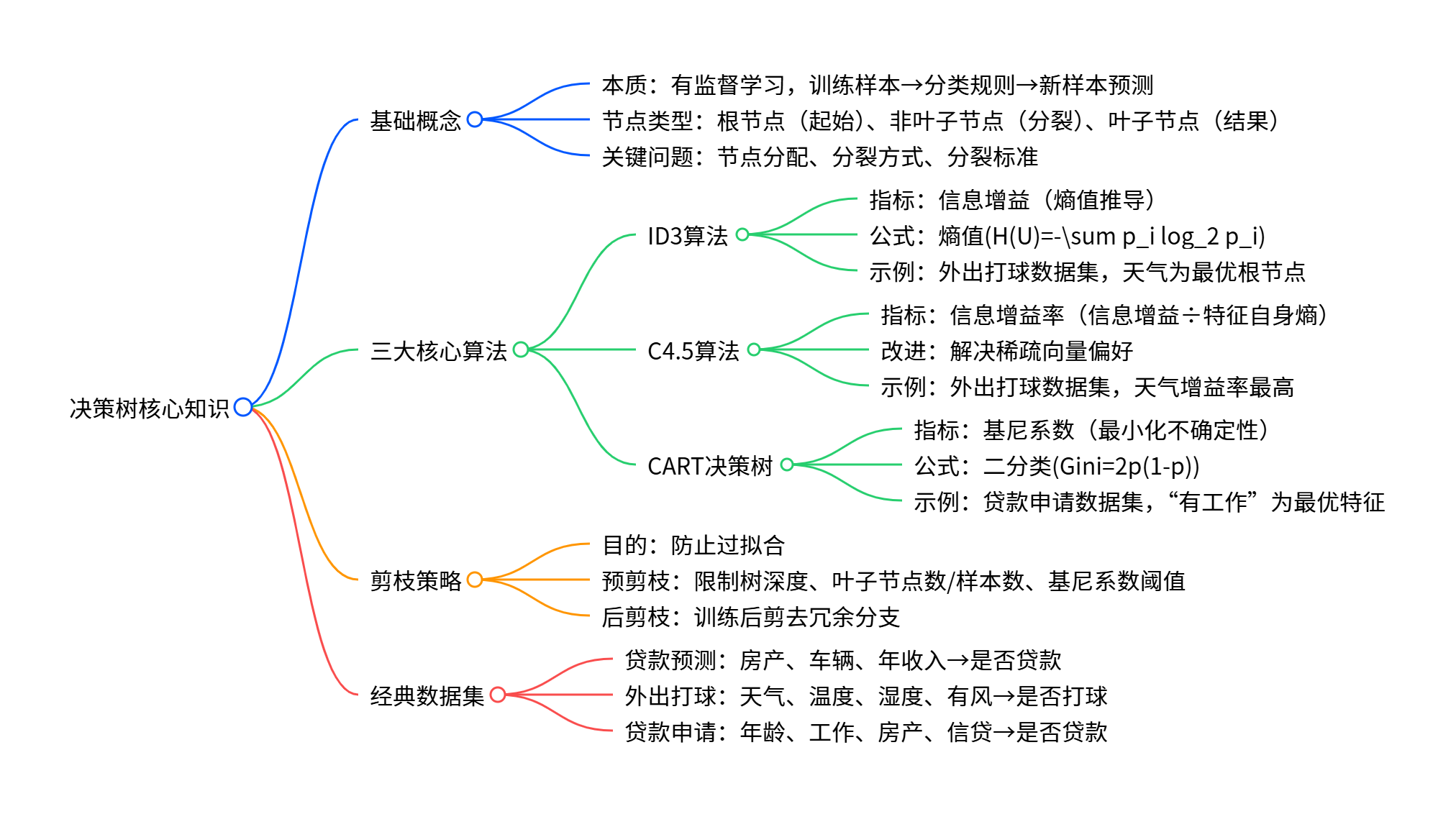
一、决策树基础核心
- 定义与核心逻辑本质：属于有监督学习，通过学习训练样本建立分类规则，对新样本进行分类预测。核心流程：所有数据从根节点出发，经非叶子节点（中间节点）逐步分裂，最终落到叶子节点
二、三大核心分类算法（节点分裂标准）
1. ID3 算法
- 核心衡量指标 ：信息增益（基于熵值计算），选择信息增益最大的特征作为分裂属性。
- 关键概念：
- 熵值：表示随机变量的不确定性（内部混乱程度），熵值越小，节点越 "纯"；
- 熵值计算公式：
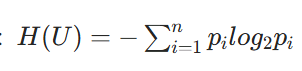
（为某类别在样本中的占比）
- 计算步骤：
- 计算标签（分类结果）的类别熵；
- 按每个特征划分样本，计算该特征对应的属性熵；
- 信息增益 = 类别熵 - 属性熵，取信息增益最大的特征分裂。
2. C4.5 算法
- 核心改进：解决 ID3 算法对稀疏向量（如编号类特征）的偏好问题。
- 核心衡量指标 ：信息增益率（信息增益与特征自身熵的比值），选择信息增益率最大的特征分裂。
- 计算步骤：
- 沿用 ID3 步骤计算类别熵、属性熵、信息增益；
- 计算该特征的自身熵（描述特征自身取值的不确定性）；
- 信息增益率 = 信息增益 ÷ 特征自身熵。
3. CART 决策树
- 核心衡量指标 ：基尼系数（衡量样本集合的不确定性，与熵值趋势一致，计算更高效），选择基尼系数最小的特征及切分点分裂。
- 关键概念：
示例：贷款申请数据集，通过计算各特征（年龄、有工作、有房等）的基尼系数，选择基尼系数最小的特征（如 "有工作"）作为最优分裂属性。
三、决策树剪枝（防止过拟合）
1. 剪枝目的
避免模型过度贴合训练数据，提升对新样本的泛化能力。
2. 剪枝方式
- 预剪枝 （训练中停止分裂）：
- 限制树的最大深度；
- 限制叶子节点的个数或每个叶子节点的最小样本数；
- 设定基尼系数阈值，当分裂后基尼系数无明显降低时停止分裂。
- 后剪枝（训练完剪去冗余分支）：文档未展开具体步骤，仅明确为核心剪枝方式之一。
四、经典示例数据集
- 贷款预测数据集：特征包括房产、车辆、年收入，分类结果为 "可以贷款""不可贷款"；
- 外出打球数据集：特征包括天气（晴天 / 阴天 / 雨天）、温度（热 / 温和 / 凉爽）、湿度（高 / 正常）、有风（是 / 否），分类结果为 "打球""不打球"；
- 贷款申请详细数据集：特征包括年龄、有工作、有自己的房子、信贷情况，分类结果为 "同意贷款""拒绝贷款"。
三大算法对比表格：
|----------|------------|----------------------------------------------------------------------------------------------------------------------------|--------------------------|----------------------|
| 算法类型 | 核心衡量指标 | 核心公式 / 计算逻辑 | 关键特点 | 适用场景 |
| ID3 算法 | 信息增益（基于熵值） | 1.熵值：H(U)=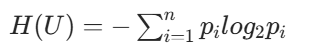
2. 信息增益 = 类别熵 - 属性熵 | 熵值越小节点越 "纯"，优先选信息增益最大的特征 | 特征取值较少、无稀疏向量的场景 |
| C4.5 算法 | 信息增益率 | 1. 信息增益（同 ID3） 2. 信息增益率 = 信息增益 ÷ 特征自身熵 | 解决 ID3 对稀疏向量的偏好问题，更稳定 | 存在编号类稀疏特征、特征取值不均衡的场景 |
| CART 决策树 | 基尼系数 | 1. 基尼系数：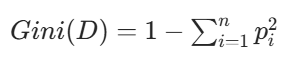
(二分类化简为2p（1-p）) 2.分裂后基尼系数=子集占比*子集基尼系数之和 | 计算效率高于熵值，支持二分类 / 回归 | 追求高效计算、需要处理回归任务的场景 |
三大算法 Python 完整实现代码（可直接运行）
基于经典外出打球数据集实现 ID3、C4.5、CART 决策树，包含数据预处理、核心指标计算、树的构建与预测
- 环境依赖（提前安装）
bash
pip install pandas numpy scikit-learn- 完整实现代码
python
import pandas as pd
import numpy as np
from math import log2
# ===================== 1. 构建经典外出打球数据集 =====================
def create_play_tennis_data():
"""创建外出打球数据集：特征为天气、温度、湿度、有风，标签为是否打球"""
data = {
'天气': ['晴天', '晴天', '阴天', '雨天', '雨天', '雨天', '阴天', '晴天', '晴天', '雨天', '晴天', '阴天', '阴天', '雨天'],
'温度': ['热', '热', '热', '温和', '凉', '凉', '凉', '温和', '凉', '温和', '温和', '温和', '热', '温和'],
'湿度': ['高', '高', '高', '高', '正常', '正常', '正常', '高', '正常', '正常', '正常', '高', '正常', '高'],
'有风': ['否', '是', '否', '否', '否', '是', '是', '否', '否', '否', '是', '是', '否', '是'],
'是否打球': ['否', '否', '是', '是', '是', '否', '是', '否', '是', '是', '是', '是', '是', '否']
}
df = pd.DataFrame(data)
# 特征列 + 标签列
features = df.columns[:-1].tolist()
label = df.columns[-1]
return df, features, label
# ===================== 2. 通用工具函数 =====================
def get_unique_label_count(data, label):
"""统计标签列的类别及数量，返回{类别:数量}"""
return data[label].value_counts().to_dict()
def choose_best_feature(data, features, label, method='ID3'):
"""
选择最优分裂特征
:param method: 算法类型 ID3/C4.5/CART
:return: 最优特征名
"""
# 总样本数
total_samples = len(data)
# 1. 计算标签的基础指标（ID3/C4.5：熵值；CART：基尼系数）
if method in ['ID3', 'C4.5']:
base_metric = calculate_entropy(data, label)
else:
base_metric = calculate_gini(data, label)
best_metric = -float('inf') # 最优指标值
best_feature = None # 最优特征
for feat in features:
# 按当前特征的不同取值划分子集
feat_unique_vals = data[feat].unique()
sub_metric_sum = 0 # 子集指标加权和
feat_entropy = 0 # C4.5需要：特征自身的熵值
for val in feat_unique_vals:
# 特征取值为val的子集
sub_data = data[data[feat] == val]
sub_samples = len(sub_data)
# 子集占比
ratio = sub_samples / total_samples
# 计算子集的指标并加权求和
if method in ['ID3', 'C4.5']:
sub_ent = calculate_entropy(sub_data, label)
sub_metric_sum += ratio * sub_ent
# C4.5：计算特征自身的熵值
feat_entropy += -ratio * log2(ratio) if ratio != 0 else 0
else:
sub_gini = calculate_gini(sub_data, label)
sub_metric_sum += ratio * sub_gini
# 计算当前特征的核心指标
if method == 'ID3':
# ID3：信息增益 = 基础熵 - 子集熵加权和
current_metric = base_metric - sub_metric_sum
elif method == 'C4.5':
# C4.5：信息增益率 = 信息增益 / 特征自身熵（避免除0）
info_gain = base_metric - sub_metric_sum
current_metric = info_gain / (feat_entropy + 1e-8)
else:
# CART：基尼系数减少量 = 基础基尼 - 子集基尼加权和（越大越优）
current_metric = base_metric - sub_metric_sum
# 更新最优特征
if current_metric > best_metric:
best_metric = current_metric
best_feature = feat
return best_feature
def majority_vote(label_count):
"""投票法：标签数量最多的类别（用于叶子节点无特征可分的情况）"""
return max(label_count, key=label_count.get)
# ===================== 3. ID3/C4.5 核心指标：熵值 + 信息增益 =====================
def calculate_entropy(data, label):
"""计算熵值 H = -Σ(p_i * log2(p_i))，p_i为类别i的占比"""
label_count = get_unique_label_count(data, label)
entropy = 0.0
total = len(data)
for count in label_count.values():
p = count / total
entropy -= p * log2(p) if p != 0 else 0
return entropy
# ===================== 4. CART 核心指标：基尼系数 =====================
def calculate_gini(data, label):
"""计算基尼系数 Gini = 1 - Σ(p_i^2)"""
label_count = get_unique_label_count(data, label)
gini = 1.0
total = len(data)
for count in label_count.values():
p = count / total
gini -= p ** 2
return gini
# ===================== 5. 决策树构建（递归） =====================
def create_tree(data, features, label, method='ID3'):
"""
递归构建决策树
:return: 决策树字典（如{'天气': {'晴天': {'湿度': {...}}, '阴天': '是', ...}}）
"""
label_list = data[label].tolist()
# 终止条件1：所有样本标签相同，直接返回该标签
if label_list.count(label_list[0]) == len(label_list):
return label_list[0]
# 终止条件2：无特征可分，返回投票最多的标签
if len(features) == 0:
return majority_vote(get_unique_label_count(data, label))
# 选择最优分裂特征
best_feat = choose_best_feature(data, features, label, method)
# 初始化决策树
decision_tree = {best_feat: {}}
# 移除已选最优特征（避免重复分裂）
remaining_feats = [f for f in features if f != best_feat]
# 按最优特征的不同取值递归构建子树
for val in data[best_feat].unique():
sub_data = data[data[best_feat] == val]
decision_tree[best_feat][val] = create_tree(sub_data, remaining_feats, label, method)
return decision_tree
# ===================== 6. 决策树预测 =====================
def predict(tree, sample):
"""
单样本预测
:param tree: 构建好的决策树
:param sample: 单样本字典（如{'天气':'阴天', '温度':'温和', '湿度':'正常', '有风':'否'}）
:return: 预测标签（是/否）
"""
# 根节点特征
root_feat = next(iter(tree.keys()))
# 根节点下的子树
root_feat_dict = tree[root_feat]
# 样本的根特征取值
sample_val = sample[root_feat]
# 递归查找预测结果
next_node = root_feat_dict[sample_val]
if isinstance(next_node, dict):
# 子节点是树，继续递归
return predict(next_node, sample)
else:
# 子节点是标签，返回结果
return next_node
# ===================== 7. 主函数（测试三大算法） =====================
if __name__ == '__main__':
# 1. 加载数据
df, features, label = create_play_tennis_data()
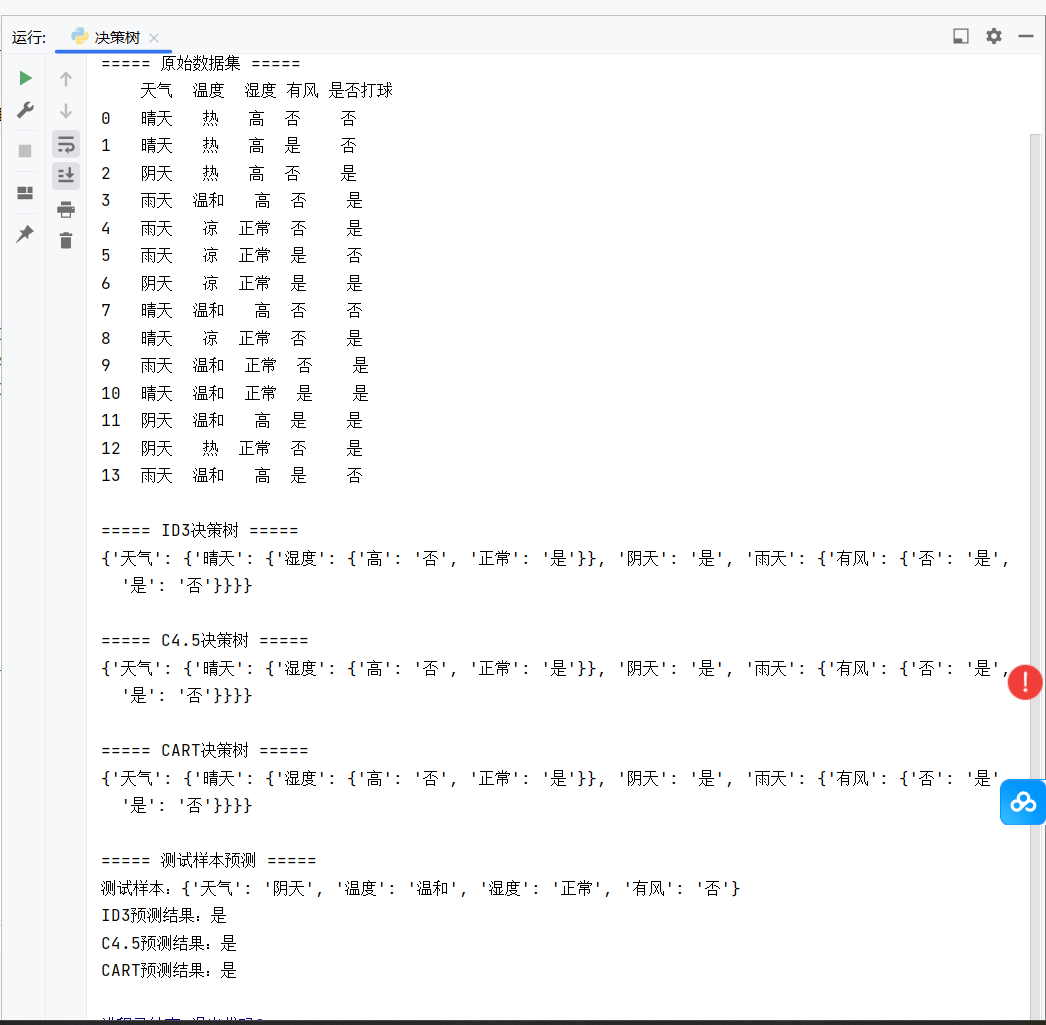
print("===== 原始数据集 =====")
print(df)
# 2. 分别构建ID3、C4.5、CART决策树
id3_tree = create_tree(df, features, label, method='ID3')
c45_tree = create_tree(df, features, label, method='C4.5')
cart_tree = create_tree(df, features, label, method='CART')
print("\n===== ID3决策树 =====")
print(id3_tree)
print("\n===== C4.5决策树 =====")
print(c45_tree)
print("\n===== CART决策树 =====")
print(cart_tree)
# 3. 测试预测（单样本）
test_sample = {'天气':'阴天', '温度':'温和', '湿度':'正常', '有风':'否'}
id3_pred = predict(id3_tree, test_sample)
c45_pred = predict(c45_tree, test_sample)
cart_pred = predict(cart_tree, test_sample)
print(f"\n===== 测试样本预测 =====")
print(f"测试样本：{test_sample}")
print(f"ID3预测结果：{id3_pred}")
print(f"C4.5预测结果：{c45_pred}")
print(f"CART预测结果：{cart_pred}")- 输出原始数据集 、三大算法的决策树结构（字典形式，直观体现节点分裂逻辑）；
- 测试样本
{'天气':'阴天', '温度':'温和', '湿度':'正常', '有风':'否'}三大算法均预测是（符合业务逻辑）； - 可自行修改
test_sample测试不同场景，也可替换为自己的数据集（需保证特征为离散型，CART 可扩展连续型）。
运行结果：