带分数正则的一致性蒸馏

预备知识

在扩散模型的"物理学时代"，人们想着"如果我把真实数据一点一点弄脏，再学会反着洗干净，能不能生成？"

于是精心设计了满足随机微分方程（SDE）的扩散过程，T是一个大于零的常数，和分别是漂移和扩散系数，表示标准布朗运动，的分布满足，。

这个前向加噪过程可以写成一个高斯过程，即（和分别是信号强度和噪声调度），构成一个闭合高斯族，状态转移概率为（为信噪比）。补充两对系数之间的关系：，

根据贝叶斯公式构造反向过程的状态转移概率（扩散过程的马尔可夫性），三个高斯乘除的结果仍是一个高斯分布，均值为，方差为。现实中我们的目标就是得到，并不能事先知道，只能用一个去噪网络来估计。

方差保持（VP）的方案选择，最后落在一个标准高斯分布，易采样、各向同性、数学干净、反向推导简单、KL损失可写成闭合形式、工程友好。在反向过程中，模型预测噪声，就能构造，去噪扩散概率模型（DDPM）会据此构造状态转移分布（均值为，方差为），从中采样下一个状态，需要大量次数迭代。而去噪扩散隐式模型（DDIM）选择复用预测的噪声和执行前向，得到下一状态，没有一点随机性。可以通过一个随机性调制参数，取，调节采样，当时属于DDIM，时属于DDPM。 补充一下，VP有，其中是人为设置的"噪声调度"，决定了信号衰减速度，也决定了噪声如何进入系统，可选"线性调度"、"余弦调度"......在离散场景下，有。

为什么DDIM能work？这个SDE有个重要性质是存在一个常微分方程（probability flow ODE），它在t时得到的解分布也满足，其中是的分数函数score（对数概率，描述固定时间下，数据分布在样本空间中的局部上升方向，例如在VP中有，所以。我们可以在反向还原数据的过程中不去通过构造高斯分布随机采样，而是通过ODE求解器确定性采样，而DDIM便是沿着概率流从噪声回到了数据。

Elucidating the Design Space of Diffusion-Based Generative Models（Karras et al. 2022)提出了一套扩散模型体系EDM，选择（方差爆炸VE）（漂移系数），噪声强度时才是高斯分布，score更自然、数值更稳定、ODE轨迹更平滑。比如说设置扩散系数，代入PF ODE得到，有（卷积操作）。让模型直接在不同的噪声水平下，预测干净样本，其中这些是预先设置的函数，使得在不同噪声水平下网络看到的数值尺度是稳定的，网络只需学"真正的去噪残差"，以稳定训练。

VP名字的来由是"如果，那么"，以此类推VP均值衰减但和方差耦合，用"噪声+衰减"慢慢淹没数据；VE均值恒等，用"纯噪声"把数据炸开。

其实扩散模型真正需要的是一个已知的简单的分布和一条从数据分布到该分布的连续路径，建模选择可以五花八门。于是有人放弃了布朗运动，选用了一条更直接的路径------前向插值，在这条路径下，训练模型去匹配真实的速度场，即"flow matching"。训练流程：采样、、，构造插值样本，对这个线性插值路径的真实速度场为，同时网络预测速度，计算损失；纯ODE流推理流程：初始化，反向过程就是求解ODE，比如用Euler求解器，有，直到得到生成样本。或者每一步重构，再加噪重新采样，于是防止速度场误差累积，保证样本多样性，且随机性在去噪后期会自动消失（wan2.1 t2v就是这么做的）。

一致性模型

Consistency Models（23'），还是基于score-based diffusion/EDM，选择路径。

澄清一下，在扩散模型中，分数函数描述的是固定时间下，数据分布在样本空间中的局部上升方向，并不是样本随时间演化的切线斜率或者说去噪方向，那么为什么空间方向可以指导时间演化方向呢？因为时间并非独立的自由维度，只是"噪声强度/分布形状变化"的参数，而分布随时间变化，完全由空间上的概率流（probability flow）决定，从上文的PF ODE可见一斑。

EDM在不同的噪声水平下，通过下列带强"preconditioning"性质的式子预测干净样本，其中这些是预先设置的函数，利用我们已知的噪声统计结构，在模型前后引入解析尺度因子和 skip connection，把一个跨多个数量级的去噪问题变成一个数值条件良好的残差学习问题：输入preconditioning用于将不同下的拉到相似的数值范围，通常有，skip connection使得网络无需从零开始学习"保留原图"，只在需要时修正，输出preconditioning则用于控制残差幅度，确保输出与真实同尺度。

EDM于是定义了一个确定性ODE：，然后使解码器，没有随机性又数值行为稳定。形式不同，但依旧等价于score matching，可以从解析出score（）

后面可以看到，这个一致性模型论文的很多地方都遵从了EDM的设置，以及一致性蒸馏的教师模型也是源自EDM。

一致性

"一致性"就是输入轨迹上任何一点，模型都能得到原始数据，有了它就能从直接变成了（像GANs、VAEs、归一化流那样），同时也支持通过多迭代几次提升质量，表现出零样本数据编辑能力（像迭代去噪的扩散模型那样，能去噪、上色、超分辨率、去除遮挡......）。

定义一致性函数，针对同在PF ODE轨迹上的任意两点，都有，边界条件限定是一个恒等函数，满足这个限制有两种参数化策略。假设有一个形式不受限的网络，输出的维度和一样，第一种方法就直接

第二种为，其中，，且和要可导，这样在那就可微了，对训练来说很重要。作者采用后者。

假设已有一个训练好的一致性模型，可以从初始分布中采样，评估模型单步生成的效果，也可以交替去噪和加噪过程评估质量提升能力，如下

实践中的选取是一个贪心算法，采用三元组搜索，每次精确定位一个时间点，以优化所有样本的FID（不懂T^T）。

蒸馏一个预训练好的分数模型

假设已有一个扩散模型，离散化时间（为了避免数值不稳定性，设置一个很小的正数，在就停止求解），还是遵循Karras et al. (2022)的设置，定义，其中，图片像素值缩放到，设、。当足够大的时候，就能从通过数值ODE求解器离散的一步得到，即

其中表示一步ODE求解器的更新函数，比如Euler求解器，把分数代入PF ODE后，得到，对应的更新过程变成

用这个扩散模型的权重作为初始权重，然后蒸馏：你先从数据集中采样一个数据点，从均匀分布中取，采样（加个高斯噪声），模型计算分数，ODE求解器离散一步，算出，得到成对的。设计一致性蒸馏损失函数

其中是一个恒大于0的权重函数，所有任务和数据集上都表现不错；采用随机梯度下降更新模型参数，取一系列历史值进行加权平均，构成"running average"：采用指数滑动平均（EMA），给定下降率，取；度量函数，仅时取等，比如、、LPIPS（learned perceptual image patch similarity）。

对标到深度强化学习（deep reinforcement learning）和基于动量的对比学习（momentum based contrastive learning），是"目标网络"，是"在线网络"。

在强化学习中，在线网络负责实时决策和动作选择，其参数在每个训练批次后都会通过反向传播持续更新，在传统的Q- learning算法中，每次选择都最优动作，Q值往往被高估，偏差在训练过程中累积，导致学习效率下降甚至训练发散，于是引入一个独立且更新延迟的目标网络，专为损失函数提供稳定的目标值，有效缓解偏差累积速度。目标模型周期更新的策略分为硬更新（直接将在线网络参数复制到目标网络，即）和软更新（设定权重混合在线网络和目标网络的参数，比如这里的EMA），这里就是采用后者，再加上"stopgrad"操作，防止坍塌，稳定训练、提升性能。

下面基于渐进分析给一致性蒸馏提供理论依据。（感觉要看不懂，先试试）

定理1（编号遵从论文）：取最大时间间隔，表示PF ODE的一致性函数，假设满足利普希茨条件（存在，任取，对任意和，都有），假设任取，在调用ODE求解器时的局部误差有上界，其中，那么，如果，就有。

当蒸馏过程收敛时便有，损失为0，定理1就表示只要ODE求解器的步幅够小，一致性模型能在任意点都精确。设置边界条件能有效避免训练成平凡解。

一致性蒸馏损失可以扩展到无限时间步（），所得的连续时间损失函数无需指定和时间步，但这些函数涉及雅可比-向量积的计算，需使用前向模式自动微分来实现高效计算，而某些深度学习框架可能支持一般，详情再说吧...（看不懂捏斯密达～）（再挣扎一下）

给定一个二阶连续可导的矩阵函数，定义矩阵和，有、，将针对的雅可比矩阵表示成，当时有以下结论

定理3：令，其中是一个严格单调且满足、的函数，假设在[0,1]连续可导，三阶连续可导且有界，两阶连续连续且一二阶有界，进一步假设权重函数有界、，于是用Euler求解器一致性蒸馏，就有，等式右侧定义为，其中，，这个期望值就是在、、、的情景下得到的。

单独训练一个一致性模型

可以通过下列无偏估计避免预训练分数模型：，其中、，也就是说，可以用来近似。

定理2：取最大时间间隔，假设和都二阶导数存在且有界，权重函数有界，，进一步假设采用Euler ODE求解器，且预训练分数模型能准确预测，即，于是，定义一致性训练损失（CT）为

其中，要是的话，。证明源于泰勒级数展开和分数函数定义。完整证明再说吧...下降的比慢，当且时将成为损失的主要部分。随机初始化一致性模型权重，训练流程如下

其中N不再固定，而是用调度函数渐进增加，因为当小的时候，相较于方差更小但偏差更大，能在训练开始带来更快的收敛，而在训练结束时就会希望更小的偏差了，另外也应该逐渐变大。一致性训练损失同样可以扩展到连续时间上，此时就不需要和的调度函数，但也需要前向模式自动微分来实现高效计算，这里就无须担忧偏差了。

实验

作者在图片数据集上测试一致性蒸馏和训练，包括CIFAR-10、ImageNet 64x64、LSUN Bedroom 26x256和LSUN Cat 256x256，生成质量用（FID）、（IS）、和来衡量。首先在CIFAR-10上做了一系列试验来理解不同超参对性能的影响，如度量函数、OD求解器、CD的离散步数N，以及CT中动态调度函数和的影响：

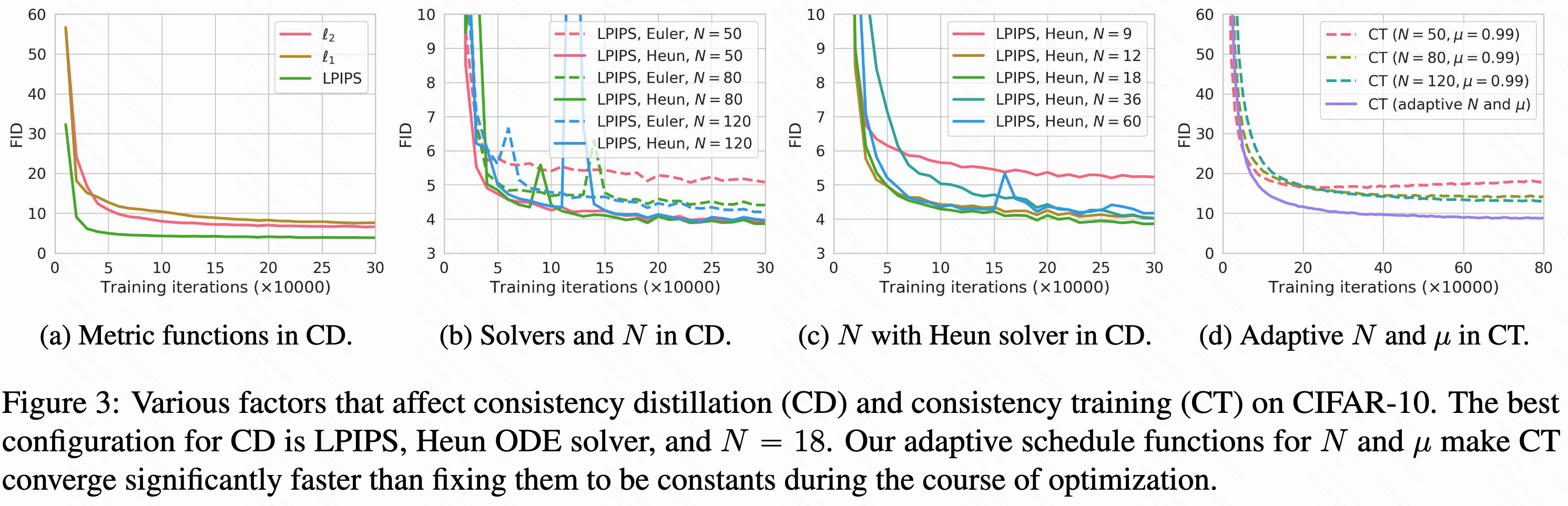
LPIPS是为衡量自然图像间相似性专设的，自然更适合CIFAR-10的图片；针对CD，Heun ODE求解器（阶数高点）和N=18（N达到一定程度后，CD的质量对N就不敏感了，其他数据集可能换一下）的设置是最好的选择，这和Karras et al. (2022 核心观点是预测去噪后的数据在数值上最自然)是对齐的。在CT中针对不同分辨率的和设计不同。

针对ODE求解器，什么是Euler's forward method（欧拉前向法）什么是Heun's second order method（Heun 二阶方法）？标准常微分方程形式如，时常没有解析解，需用数值方法步步逼近。设步长为，时间点为。欧拉前向法就是"在当前点沿着切线走一步"，即，属于一阶方法；而Heun属于Runge-Kutta二阶方法（全局误差在），先用Euler算一个"猜测值"，再用两点斜率的平均值做修正，即。

当时只有渐进蒸馏和一致性蒸馏一样不需要自己合成数据，能作为直接比较的对象（知识蒸馏和DFNO都是让教师模型从噪声还原成原始数据，形成原始数据和去噪数据对，作为训练集，制备过程老费劲了），结果如下

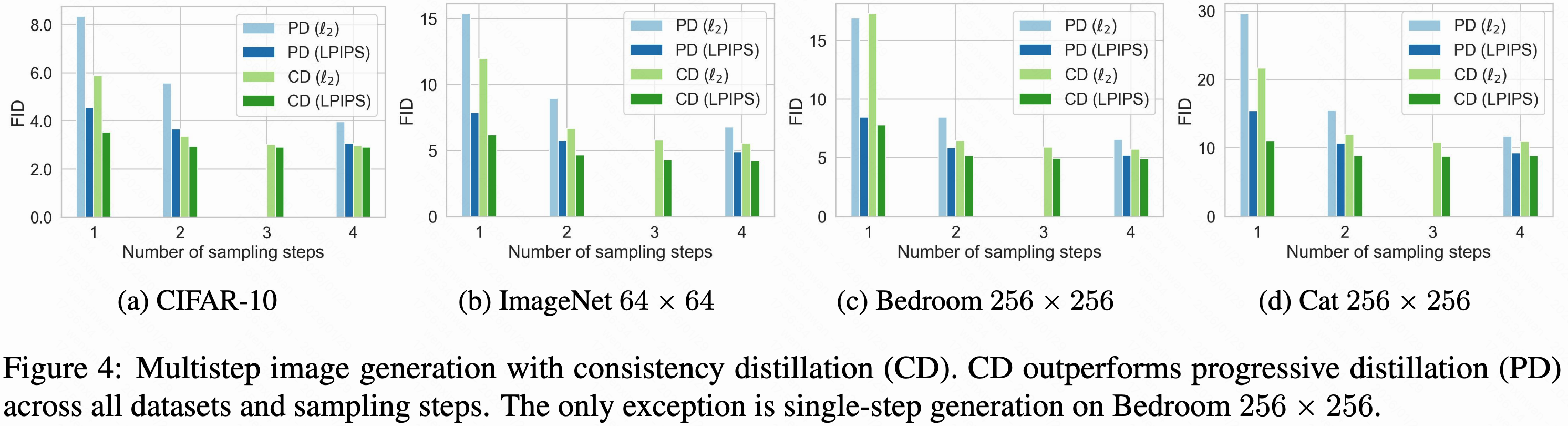
也在单步和两步的设置下，比较了CT和其他生成式模型，即使没接触过原始模型，它的质量也能匹配甚至超过渐进蒸馏出来的单步采样器。

连续时间上的一致性模型

Simplifying, Stabilizing and Scaling Continuous-Time Consistency Models（24'）

问题是在ODE求解器根据教师输出求解时存在离散误差，且需事先设计如何调度时间步。连续时间一致性模型则限制，选择度量函数时，上述损失关于的梯度会收敛于，其中全导数表示在沿着教师轨迹PF-ODE的切线方向。

为了保证训练的稳定性，TrigFlow框架在参数化、网络架构、训练目标上都进行了改进，提出sCM（simple stable scalable）。

训练不稳定性的来源在哪？展开，其中 由教师模型提供（蒸馏）或者代导数公式得到（训练）。经验上，、、都相对比较稳定，剩下，而对输入不敏感，只能是，将其按下式分解：，逐项优化-》

1. 一致时间转化；

2. 位置编码, （傅立叶/三角时间编码采用会引入不稳定因素，通过对c求偏导，可以看到过大的傅立叶系数s会导致剧烈震荡）；

3. 自适应双重归一化，是像素空间的正则化

于是在TrigFlow框架下，梯度可简化成。为了进一步的稳定训练，还做了

1. 梯度归一化：替换成，凭经验设置c=0.1，也可以施加裁剪；

2. 训练权重函数，而不是手工设计，省了调参的麻烦，性能好不少，也没啥训练成本。作为一个和无关的矩阵，有，变成了一个MSE目标的梯度，结合先验分布，可以通过下列损失同时训练网络和自适应权重：（因为噪声强度,跨度很大，如果线性采样t的话训练过程会严重偏向于大噪声，实际是从一个对数正则分布中采样，即）

3. 梯度预热技术：系数替换成，r在前10k次训练迭代中从0线性增长到1。

PS：伪代码中的 ，根据一致性模型的参数化定义，展开。

1. 在计算这个切线时如何在保证数值精度的同时支持存储高效的注意力计算（FP16 、Flash Attention）？雅可比矩阵计算重排。

表示根据输入和切线，对做雅可比矩阵乘JVP，t接近0或时中间层容易溢出，建议重排计算：，变成了根据输入和切线，能减少溢出问题。

在原始注意力计算中，已有QKV，算，，O=PV。

在Flash Attention前向计算时，假设被切成了n块，每块，针对，初始化两个全局变量、和一个全零输出向量。流式读取每对，计算，找出其中行最大值，记录，为当前块计算，更新"全局指数和"，更新输出，更新"全局最大"。遍历完后补上分母。整个前向没算JVP，得额外操作一下。

回到原始注意力，设定分别是SPVO对时间的导数，那么注意力的JVP运算就是：，，换Flash Attention把拆块后，所有涉及它的矩阵运算也都要用m逐步更新，具体地，针对，初始化三个全局变量、、和三个全零输出向量。流式读取每对，计算，，然后找出中的最大值，记录，为当前块计算，更新"全局指数和"、、，同时为当前块计算，更新、，最后更新"全局最大"。遍历完后补上分母，组装。

各层前向时也要传播梯度，下面是改写RMS层的一个样例

训练过程中不涉及离散时间步的设计，与采样器解耦，选择多步去噪时流程和前述的多步一致性采样流程一致。