02计算机组成原理-逻辑运算符与字符表示

1.位运算
- 1.1按位与&（AND）
- 1.2按位或|（OR）
- 1.3按位异或^（XOR）
- 1.4非运算~（NOT）
- [1.5左移（Left Shift）](#1.5左移（Left Shift）)
- [1.6右移（Right Shift）](#1.6右移（Right Shift）)
2.字符表示

来做一道例题巩固一下上堂博客学的：十进制的数-66，按其补码的形式存放在一个8位的寄存器中，问该寄存器的内容是？

-66我们可以看成-（64+2），所以-66的原码是：1100 0010，由于是负数，我们对负数的补码操作是原码的符号位不变，其余数值位取反加1得：1011 1110

1011=1+2+8=B（十六进制下）1110=E，所以应该是BEH。

1.位运算

位运算：位操作是对整数或其他二进制表示的数据的每个位进行单独操作

虽然早期的计算机仅对整字进行操作，但人们很快就发现，对字中由若干位组成的字段甚至对单个位进行操作是很有用的，如:

位级操作：在计算机硬件和软件层面支持对一个字中的单个或一组位进行操作，这对于实现诸如错误检测（如奇偶校验、CRC校验）、数据压缩、编码解码（如ASCII到EBCDIC转换）、权限控制（如访问控制位）以及硬件接口信号处理等任务至关重要。

布尔逻辑：逻辑门电路的设计和数字逻辑的应用也要求能够对位进行AND、OR、NOT等逻辑操作，这在计算机内部的控制电路中是基础性的工作。

打包和拆包：在通信协议、数据格式化等领域，经常需要将多个小的数据元素（比如单个字符或标志位）组合成一个较大的字，或者从一个字中提取特定的位字段，这些操作都依赖于位级操作指令。

接下来来看一个打包拆包的过程：

打包（Packing）：假设有一个结构体，包含两个8位的字符变量（在C语言中）：

c 复制代码

struct {
unsigned char a: 4; // 使用了4位
unsigned char b: 3; // 使用了3位
unsigned char c: 1; // 使用了1位
} bit_fields;
// 打包操作：将这三个独立的位字段组合到一个完整的字节中
bit_fields.a = 10; // 设置a为十进制的10，即二进制的1010
bit_fields.b = 5; // 设置b为十进制的5，即二进制的101
bit_fields.c = 1; // 设置c为1
// 此时，整个字节可能是这样的（具体取决于编译器的实现方式）：
// 二进制表示：1010 101 1，这个字节包含了三个位字段的数据

拆包（Unpacking）：反向的过程就是从一个字节中提取出特定的位字段：

c 复制代码

unsigned char packed_byte = ...; // 假设这是上面打包得到的字节
// 拆包操作：从packed_byte中获取各个位字段的值
bit_fields.a = (packed_byte >> 4) & 0x0F; // 右移4位并按位与，得到a的值
bit_fields.b = (packed_byte >> 1) & 0x07; // 右移1位并按位与，得到b的值
bit_fields.c = packed_byte & 0x01; // 直接按位与，得到c的值
// 这样就从原始的packed_byte中分离出了三个独立的位字段信息

bit_fields.a = (packed_byte >> 4) & 0x0F; // 右移4位并按位与，得到a的值 这句话的意思是如下图:

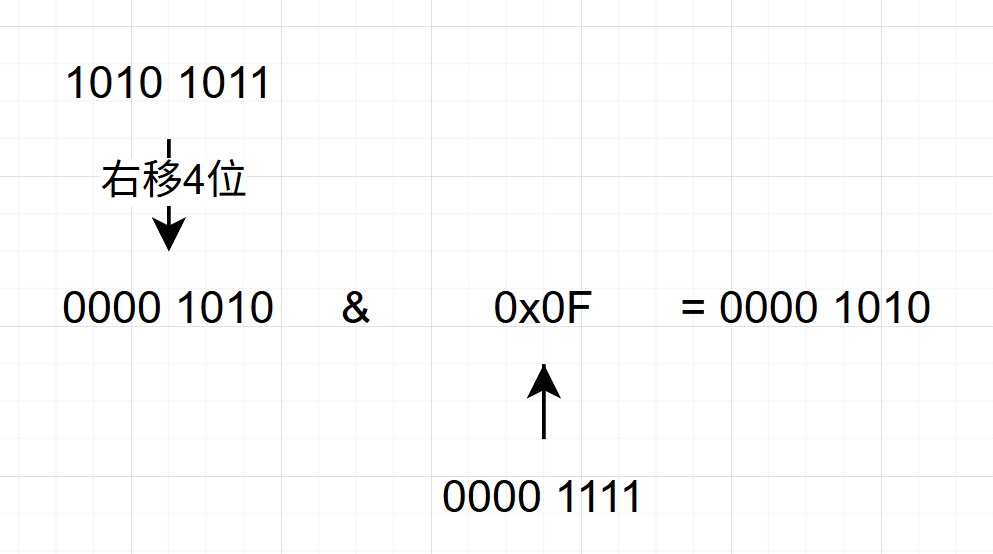
&运算就是两个相同的位置只有同时为1，运算出来才为1否则都为0

其他两句话同理。

以上例子展示了如何通过位操作对数据进行打包和拆包，这种技术常用于优化存储空间、处理网络协议数据包以及硬件接口通信等方面。

因此，现代计算机的指令集架构中通常包含了丰富的位操作指令，允许程序员直接对数据的各个位进行操作，极大地增强了程序设计的灵活性和效率。

1.1按位与&（AND）

与运算（AND）：按位与，对于两个操作数的每一个对应位，只有当两者都为1时结果才为1。

例如：计算机中的8位二进制运算：9&5=？；-9&5=？

9=0000 1001 ；5=0000 0101；（0000 1001）&（0000 0101）=0000 0001

=1，故9&5=1。

9的原码是0000 1001，所以-9的补码是原码取反加1=1111 0111；5=0000 0101；（1111 0111）&（0000 0101）=0000 0101=5，故-9&5=5。

按位与（Bitwise AND）作用：

保留某些位：原理：x&1=x,x&0=0。（x只占一位）。当您需要从一个整数中只保留特定位置为1的位时，可以使用按位与操作。例如，假设有一个8位二进制数 x = 0b10110101 ，想要保留最低4位（最低四位全是1，前面位置全是0），可以与掩码 0b00001111 进行按位与运算，结果会仅保留原数的最低4位。
清除某些位：如果想清零某个整数中的特定位，可以用一个所有位都是0，只有要清零位是1的掩码进行按位与运算。例如，要清除 x 的最高位，可以使用掩码 0b11111110进行与运算。
检查标志位：在编程中，常常利用按位与来检查变量中的某一位是否设置了特定标志。比如，一个状态字节可能有多个标志位表示不同的条件，通过与相应的位模式进行比较，可以确定这些条件是否成立。
网络地址和子网掩码计算：在网络编程中，IP地址通常用32位二进制数表示，子网掩码用于确定网络部分和主机部分。将IP地址与子网掩码做按位与运算，可以得到网络地址，即同一网络段内所有设备共享的部分。
硬件接口控制：许多硬件寄存器或端口通过特定位来控制功能或读取状态信息，程序员可以通过按位与操作读取或修改这些位字段。
数据有效性校验：某些情况下，按位与可用于简单地校验数据的有效性，如奇偶校验，通过对一组位进行与操作，可以快速判断是否有奇数个位被设置为1。

1.2按位或|（OR）

或运算（OR）：按位或，只要有一个操作数的某一位为1，结果的对应位就为1。

例如：9|5=？

9=000 1001 ；5=0000 0101；9|5=0000 1001 | 0000 0101=0000 1101=13

按位或运算的主要作用包括：

设置标志位：原理：x|0=x,x|1=1

在处理状态字或其他包含多个标志的变量时，可以利用按位或来快速设置某个特定的标志位。例如，若要设置一个32位变量的第5位为1，可将其与掩码0b00100000 进行按位或运算。
合并数据：

当需要合并两个独立的数据集但不关心彼此冲突的位时，可以用按位或操作将它们结合在一起。比如，存储用户权限时，不同的权限可以通过各自的位表示，多个权限通过按位或组合到一起形成完整的权限集合。

例如，在计算机科学中，我们常常需要管理一组标志或属性，每个属性用一个单独的比特位来表示是否存在（1代表存在，0代表不存在）。

假设你有一个用户权限系统，其中：

权限A对应于第0位（即2^0=1）

权限B对应于第1位（即2^1=2）

权限C对应于第2位（即2^2=4）

如果用户1拥有权限A和权限C，则其权限可以表示为：
user1_permissions = 0b0101 # 这是一个二进制数，等价于十进制的5

另一个用户2可能只拥有权限B：
user2_permissions = 0b0010 # 这是一个二进制数，等价于十进制的2

现在，如果你想合并这两个用户的权限，使得结果包含他们各自的所有权限，你可以使用按位或运算符 | ：
merged_permissions = user1_permissions |user2_permissions

计算后得到：
merged_permissions = 0b0111 # 这是一个二进制数，等价于十进制的7

在这个例子中，通过按位或运算，结果中的每一位都是原两个用户权限对应的位中有1的那个位置上的值。因此，合并后的权限包括了所有原始的权限位------权限A、权限B和权限C。这样，我们就完成了对两个数据集（这里指两个用户的权限集合）的合并操作。
条件赋值：

可以用来实现条件性的修改整数值。例如，在某些场景下，可能希望仅当某个条件成立时才改变某个位置的比特，这时可以先对原始值进行非条件的按位与

运算清除目标位，然后与新值按位或起来完成条件赋值。
硬件接口控制：

在与硬件通信时，设备寄存器通常有各种功能控制位，通过向这些寄存器写入经过按位或运算后的值，可以同时开启或关闭多个硬件特性或模式。

1.3按位异或^（XOR）

异或运算（XOR）：按位异或，对于两个操作数的每一位，相同则结果为0，不同则结果为1。

例如：9^5=?

9=000 1001 ；5=0000 0101；9^5=0000 1001 ^ 0000 0101=0000 1100=12

满足交换律：a^b^a=b^a^a=b

满足结合律：(a^b)^c=a^(b^c)

满足自反性：a^a=0

a^0=a

按位异或运算的主要作用包括：

不改变原始数据进行翻转特定位：
如果想更改一个变量的某个比特位而不影响其他位，可以将其与一个仅该位为1的掩码进行异或运算。例如，若要切换一个字节的最低位，可以使用 x ^=1 来实现。
交换两个变量的值（无需临时变量）：
异或运算的一个经典应用是无临时变量交换两个整数的值。假设我们有两个整数a和b，可以用下面的操作来互换它们的值： a = a ^ b; b = a ^ b; a =a ^ b; 在这个过程中，a首先记录了原a和b的异或结果，然后将这个结果再与b异或就得到了原来的a值，而此时的a经过两次异或后恢复到了原来的b值。
计算奇偶校验位：
在数据传输和存储时，异或运算常用于生成奇偶校验位，比如单个位的奇校验或偶校验。所有数据位通过异或运算得到的结果即为校验位，当数据在传输过程中发生错误时，可以通过重新计算并比较校验位来检测错误。

1.4非运算~（NOT）

非运算（NOT或Complement）：单个操作数的每位取反，0变为1，1变为0。

例如：~0=-1（8位二进制）

0：0000 0000 ，~0:1111 1111，转为原码的形式看出：1000 0001=-1

作用和用途包括：

反转二进制位：

按位非运算将操作数的每个二进制位都取反。例如，对于一个二进制数0101 ，执行按位非后结果将是 1010 。
计算数值的补码形式：

在大多数计算机系统中，负数以补码形式存储。对一个正数执行按位非操作会得到一个负数，这个负数的补码是对其绝对值的原码按位取反后再加1；反之，对一个负数执行按位非操作，则大致上可以得到该负数加1之后对应的正数（但不是绝对准确，因为溢出问题可能导致不一致）。比如对于一个正整数，其补码就是其二进制表示本身。例如，正整数5在8位二进制中表示为 00000101 。一个负数的补码表示是其绝对值的二进制表示（原码），先取反（即0变1，1变0），再加1。实际上是补码表示法下负数的特性。

比如，对于-5，,10000101，我们可以这样解释：

首先，我们将其视为一个负数。

去掉最左边的符号位（对于8位二进制数，最高位是符号位），我们得到 0000101 。

对这个数取反（即0变1，1变0），得到 1111010 ，这是-5的反码表示。

因此，再加1， ,1111 1011 是-5的补码表示。

符号位不变，其余各位取反在+1，得到1000 0101，就得到了原数。
创建掩码：

c = ~a = 0b01010101

如果想要设置整数的特定位，可以使用一个只有特定位置为1的位掩码，并将其与整数进行按位或操作。例如，要设置整数 x 的最低位，您可以使用 x|= 1; 。

要清除整数的特定位，可以使用一个除了特定位为0外其他位都为1的位掩码，并将其与整数进行按位与操作。例如，要清除整数 x 的最低位，可以使用 x &= ~1; 或者 x &= 0xFE; （假设整数是8位）。

在进行位级逻辑操作时，也可以用按位与常用于生成位掩码，用于清除或设置特定的位。比如想要清除一个整数的所有位（即将其设置为0），应该使用 x&= 0;

总之，位掩码是通过按位逻辑操作（如按位与、按位或、按位非等）来设置、清除或翻转整数的特定位的一种有效方法。
判断奇偶性：

对于一个整数，执行按位与操作 n & 1 可以判断它是否为奇数。而进一步使用按位非运算 !(n & 1) 则可以判断它是否为偶数。

1.5左移（Left Shift）

左移（Left Shift）：将一个数的所有位向左移动指定次数，空出的低位补零。

例如：a = 0b10101010

左移一位后结果是：c = a << 1 = 0b101010100

主要作用和用途包括：

乘以2的幂：
左移一位相当于将该数乘以2，因为每一位都在二进制下向高位移动了一位，并且低位补零。例如，对整数 x 执行 x << n 操作，等同于将 x 乘以2ⁿ。
设置标志位：
在一些系统编程或者硬件编程中，左移可以用来快速设置一组位中的特定位置为1，比如配置寄存器或者设置权限标志。
优化内存访问：
对于某些类型的数组或数据结构，左移可能用于根据索引快速定位元素，特别是在处理按固定字节宽度存储的数据时。

1.6右移（Right Shift）

右移（Right Shift）：将一个数的所有位向右移动指定次数，高位是符号时，可能补符号位（算术右移：保留符号位，高位补符号位的值，向下取整），也可能补0（逻辑右移：不保留符号位，高位统一补0）。

例如：a = 0b10101010，算术右移一位后的结果是（考虑符号位扩展）：c = a >> 1 = 0b11010101

作用和用途包括：

除以2的幂：
对于无符号整数，右移一位相当于将该数除以2（向下取整），因为每一位都在二进制下向低位移动了一位，高位补零。例如，对整数 x 执行 x >> n 操作，等同于将 x 除以 2^n（不考虑小数部分）。
快速除法和乘法：
当需要计算某个数与2的幂次方的商时，连续右移n位可以得到近似结果（对于正数且忽略小数部分）。对于负数，在一些系统中（如采用算术右移的系统），右移会根据符号位来填充空出的高位，这可用于保持有符号数的符号不变，实现快速除以2的幂。
提取低阶位信息：
在处理特定类型的数据编码或者标志字段时，右移可用于读取或清除最低有效位上的信息

2.字符表示

最初的计算机设计和构建主要用于进行复杂的数学计算和科学研究，但随着技术的发展与进步，人们很快意识到计算机在处理信息、数据存储和商业应用方面具有巨大的潜力。

ASCII（American Standard Code for Information Interchange，美国信息交换标准代码）是一种早期广泛采用的字符编码标准，它使用7位二进制数（一个字节的最低7位）来表示128种不同的字符，包括英文大小写字母、数字、标点符号和其他控制字符。后来，为了满足更多的字符需求，出现了扩展ASCII和其他编码方案，如ISO-8859系列和Unicode等，它们可以利用8位或更多位来表示更广泛的字符集，包括非拉丁字母、特殊符号和表情符等。

现代计算机系统普遍使用8位作为基本的数据单位------字节，并在此基础上通过组合多个字节形成更大的数据类型（如16位的短整型、32位的整型和64位的长整型），以适应各种复杂的应用场景。而如今在文本处理领域，Unicode编码已经成为主流标准，能够支持世界上几乎所有的书写系统和数千种字符。

因为字符是二进制，而数字，指令也是二进制，为了让计算机识别到我们哪些二进制是数字，我们需要应提前知道字符的长度。

字符通常被组合为字符数目可变的字符串。表示一个字符串的方式有三种选择：

长度前置：在字符串的第一个位置存储字符串的长度。这种方式允许直接通过第一个字节或几个字节快速获取字符串长度，不需要遍历整个字符串来计算长度。这种方法通常在某些低级编程环境中使用，其中内存管理非常关键。通过在字符串的开始处存储长度信息，程序可以更快地确定字符串的结束位置，而不需要遍历整个数组。然而，这种方法的一个缺点是它浪费了一个字符的空间来存储长度信息，而且它要求字符串总是分配足够的空间来存储最大可能的长度，即使实际字符串可能远没有那么长。

例如，在许多数据库系统中，字符串通常采用这种方式存储。例如，在SQLite数据库引擎中，它的 VARCHAR 类型实际上就是采用这种方式来存储字符串的。
附加长度变量：在字符串数据之后额外存储一个变量（通常是整数类型），用来记录字符串的实际长度。这种方法通常在更高级的语言或框架中使用，其中字符串可能作为更复杂数据结构的一部分。通过在一个单独的变量（如结构体成员）中存储长度信息，程序可以更有效地管理内存，并且可以在不遍历整个字符串的情况下知道字符串的长度。这种方法的缺点是它增加了额外的内存开销来存储长度信息。

例如，在某些编程语言的数据结构设计中，可能会在一个结构体中包含一个字符数组和一个长度字段。
使用特定字符作为结束符：如C语言中采用的方式，即在字符串的最后一个有效字符后面添加一个特殊的字符（通常是ASCII码值为0的空字符'\0'）来标识字符串的结尾。这种设计被称为C风格字符串，也称为null-terminated字符串。在这种情况下，字符串的实际长度需要通过遍历字符直到遇到结束符来确定。

这种方法的一个优点是它不需要额外的空间来存储长度信息，因为长度可以通过查找空字符来确定。然而，它的一个缺点是确定字符串长度需要遍历整个字符串，这可能在处理非常长的字符串时导致性能问题。每种方法都有其优缺点，选择哪种方式取决于具体的应用场景、性能需求以及内存管理策略等因素。

每种方法都有其优缺点，选择哪种方式取决于具体的应用场景、性能需求以及内存管理策略等因素。

大概先写这些吧，今天的博客就先写到这，谢谢您的观看。