02计算机组成原理-定点数乘法
前言
先来看一下十进制下的乘法运算,两个十进制的数a,b,a*b=c,这个a叫做被乘数,b是乘数,c是积。
假设a是n为数,b是m位数(n>m),c的位数最少得是n+1位,最多为n+m位。
1.二进制下的乘法
假设x y都是n位得二进制数,类比十进制,它们乘完之后这个积最多得是2n位
1.1无符号数乘法
二进制乘法其实跟十进制的乘法运算的运算原理基本一样。
只涉及0和1两种数字,每一次相乘的结果只有四种可能:
0×0=0
0×1=0,
1×0=0
1×1=1。
也是从右向左依次计算。

相乘的时候地位空着的话就补0。1010对应十进制的10,0101对应的十进制是5,积0110010对应出来的十进制是50,算出来没有问题。
如果乘数对应位上的数是1,则部分积对应的那一行就是被乘数,如果乘数对应位的数字是0,则部分积对应的那一行就全是0,图中的部分积第二行和第四行就没必要加,再来看部分积的第一行和第三行,既然都是1010的话,第三行要怎么操作才能让低位补0呢,很明显是要左移2位。
故整个运算过程可以看成,从乘数的最低位起,如果对应位数是1则把被乘数加到积上,然后乘数就往高位看一位,这是被乘数需要左移一位,如果此时乘数的这个位是1,那就把左移了一位的被乘数加到积上,如果是0则不需要加了(也可以理解为加的全是0),还有个问题如何取出乘数的从右往左的每一位?只需要把乘数右移,比如我用完乘数的最低位,我就把乘数右移一下,那这样从右往左第二位就变为最低位了。以此逻辑一直到乘数的最高位。所以无符号数乘法的本质还是加法。
1.2有符号数的原码乘法
原码乘法:符号位与数值位分开求
符号位的运算遵循:
0×0=0
1×1=0
0×1=1
1×0=1
相同则0不同则1,这个刚好跟我们计算机中的异或运算对上了,这样两个有符号数的原码乘法的符号运算就是这两个二进制数的符号位做异或运算。而知道了这个我们再去算数值位的时候就可以把符号位给丢掉了,就当作两个无符号数来算就行了。
故有符号数的原码乘法运算法则是:
1.乘积的符号位由两个乘数的符号位进行"异或"运算得到
2.乘积的数值位为两个乘数的绝对值之积,即执行无符号数乘法
现在来看在计算机的硬件上是怎么实现的:三个方框代表三个寄存器,最上面的那个寄存器是用来放被乘数的,它同时还要实现左移的功能,右边的那个寄存器用来放乘数,它同时还要实现右移的功能,最下面的寄存器是用来保存部分积和最终结果的。长得像V字型的是ALU是用来进行加法计算的:把不断移位的被乘数去和最下面寄存器里存的积不断地相加,如果乘数是1就把移位之后的被乘数和最下面存的部分积送到ALU中进行相加再送回最下面的寄存器中,如果乘数是0那就啥也不用做,只需要把乘数再右移就行了,图中的控制测试是用来判断取出的乘数的最低位是0还是1。
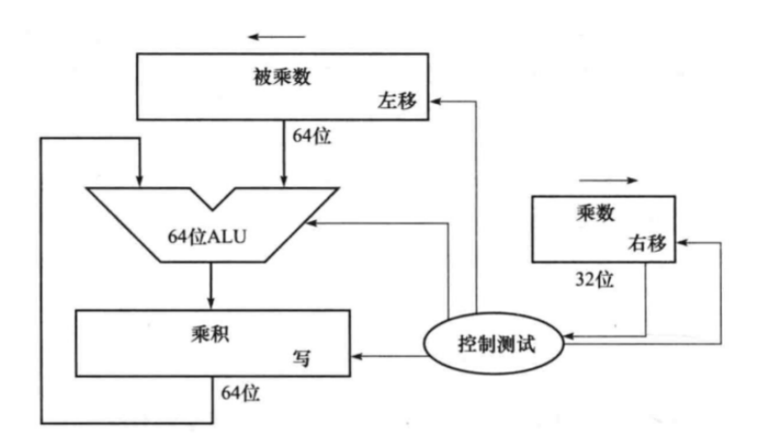
假设我们实现4位 X 4位 = 8位的乘法器,那么:
(1)需要一个8位的移位寄存器保存被乘数,他有一个左移的信号输入。
(2)需要一个8位的乘积寄存器,用来保存运算的结果。
(3)移位寄存器和乘积寄存器需要进行加法运算,所以需要一个8位的加法器,相加之后存放到乘积寄存器中。
(4)需要一个4位的乘数寄存器,同时将乘数寄存器的最低位连接右移信号,右移信号除了控制移位寄存器移位,还要控制是否进行加法运算和是否允许乘积寄存器保存当前的结果。最后还需要控制自身是否右移位。
来看一个具体的过程:
原码乘法:计算1000 X 1001(注意这里是8*9,因为符号位已经在别的地方异或算完了,这里给的就是数值位了,所以直接当数值位算就完了)
第一周期:
初始化:
将被乘数放入8位的移位寄存器中,高位补0,乘数数放在乘数寄存器中。乘积寄存器初始化为0。
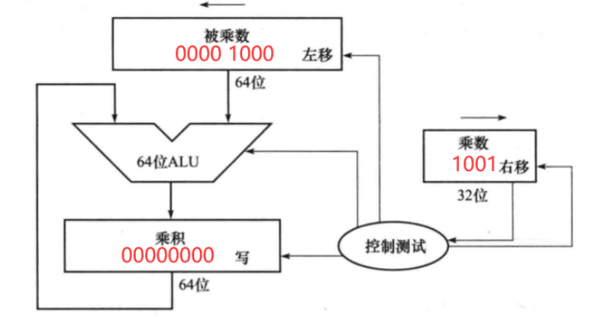
组合判断1:
乘数最低位为1,表示需要把中间变量(部分积)写到乘积寄存器中(写使能拉高),同时在下个周期将被乘数寄存器左移和乘数寄存器右移。
这个使能(Enable)是一个动词,意思是通过某种方式启用或激活某个功能或操作。在计算机术语中,使能可以是一个信号、一个开关或者一个标志位,用于控制特定的功能、设备或操作的执行。当使能信号被触发或设置为有效状态时,相关的功能或操作将被启用并开始执行;而当使能信号处于无效状态时,相关的功能或操作将被禁用或停止执行。这里写使能你就理解为一个写的信号就完了。
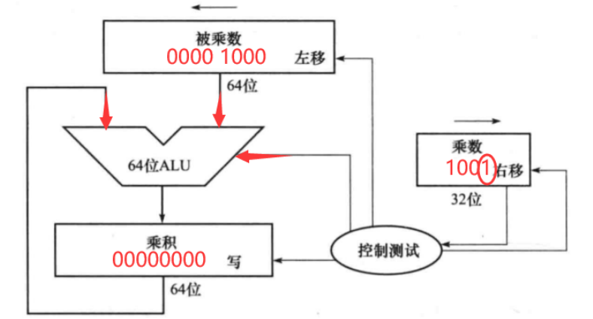
第二周期:
在第二个周期中,中间变量已经写入了乘积寄存器,同时,被乘数寄存器左移1位和乘数寄存器右移1位。
乘数寄存器右移一位时,需要进行计数,当计数为4时,表示运算结束,目前计数不是4,所以需要继续判断乘数的低位。
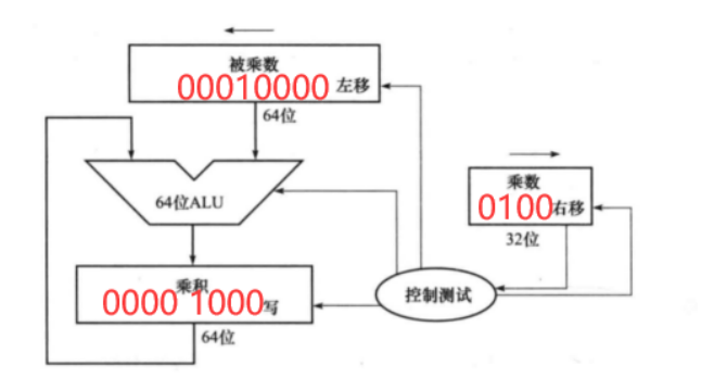
组合判断2:
被乘数低位为0,表示不需要任何操作,但需要在下个周期将被乘数寄存器左移和乘数寄存器右移。
第三周期:
在第三个周期中,中间变量没有写入乘积寄存器,同时,乘数寄存器左移1位和被乘数寄存器右移1位
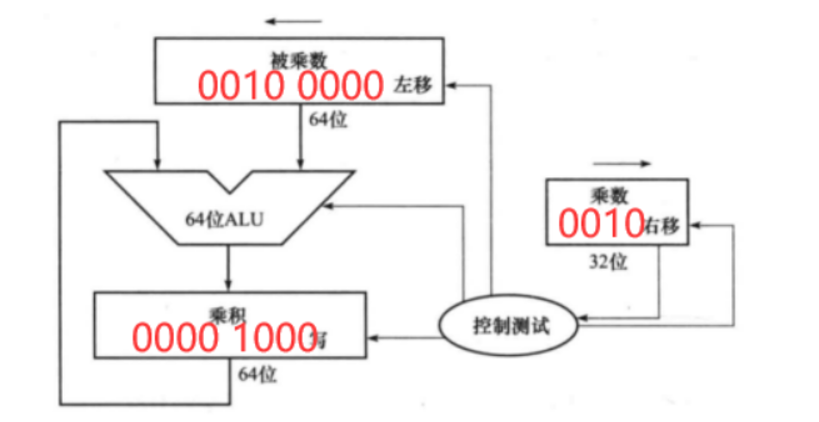
组合判断3:
被乘数低位为0,表示不需要任何操作,但需要在下个周期将乘数寄存器左移和被乘数寄存器右移。
第四周期:
在第四个周期中,中间变量没有写入乘积寄存器,同时,乘数寄存器左移1位和被乘数寄存器右移1位。
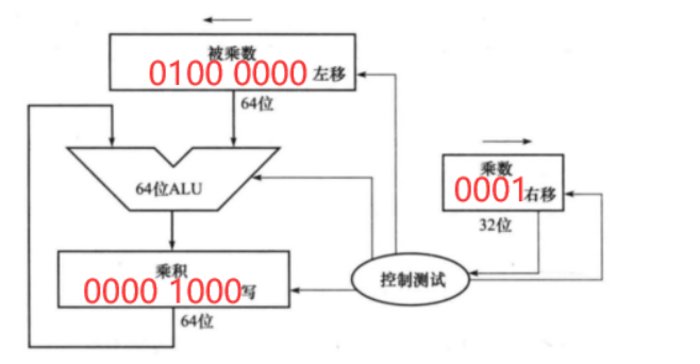
组合判断4:
乘数最低位为1,表示需要把中间变量写到乘积寄存器中(写使能拉高),同时在下个周期将被乘数寄存器左移和乘数寄存器右移。
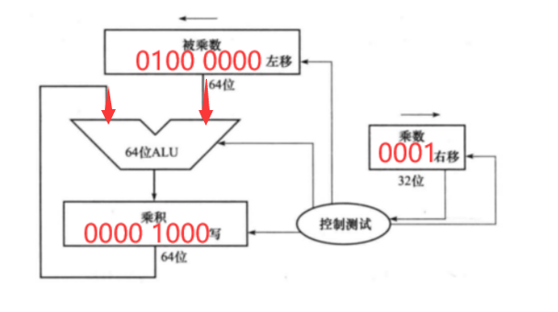
第五周期:
在第五个周期中,中间变量已经写入了乘积寄存器,同时,被乘数寄存器左移1位和乘数寄存器右移1位
判断是第4次循环,输出乘积寄存器的结果。最后发现0100 1000是72说明我们的操作是正确的。
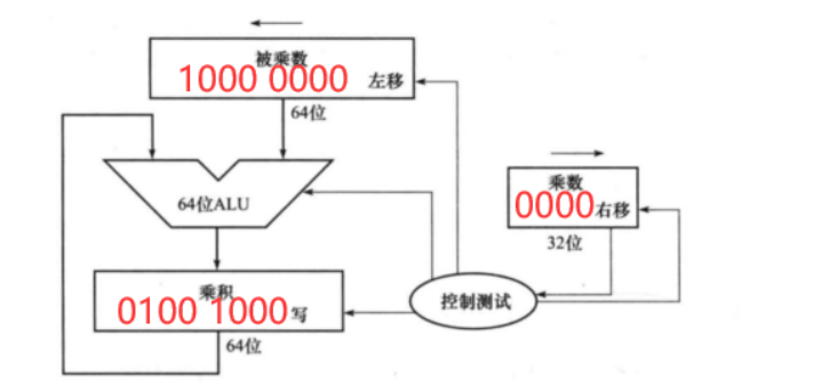
综上可以看出:在硬件实现中,乘法运算用加法和移位运算来实现。
一张图总结逻辑: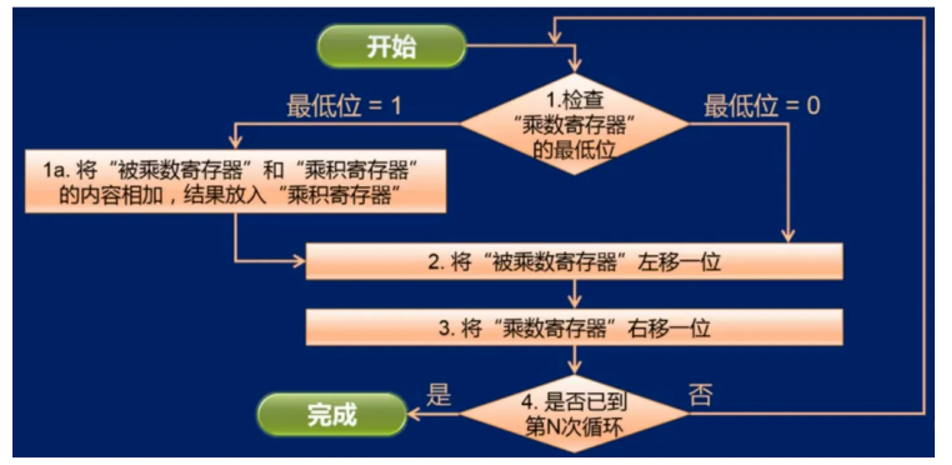
我们的电路图其实是可以简化成下面这样的(假设是32位机):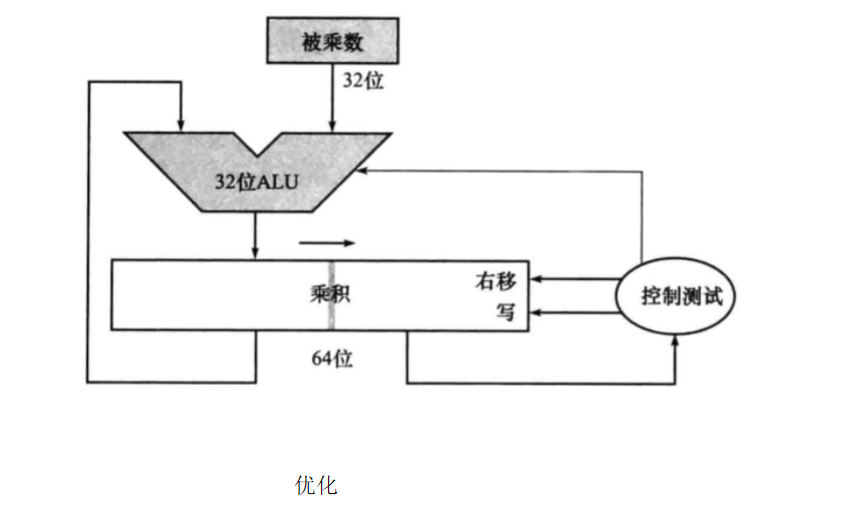
我们简化了乘数寄存器,把64位的ALU也简化成了32位的,我们的乘积寄存器分为高32位和低32位。那我们的乘数寄存器去哪了呢,大家看我们乘积寄存器的右半部分有个右移,只有乘数才会有右移操作,所以其实我们是把乘积寄存器的低32位用来放乘数同时实现右移功能,乘积寄存器的高32位用来放部分积和结果。同时大家看我们的被乘数寄存器没有左移功能,那怎么把被乘数放在合适的位置上呢,其实把乘积右移也行。比如1011*11我们可以看成先把1011放在乘积寄存器的高位上,10110000...然后把10110000...右移一位变成01011000...,因为我们的乘积寄存器是前32位和被乘数相加,所以本来应该是被乘数左移一位和部分积相加,现在部分积右移一位加上被乘数,所以加起来结果也是一样。我这里优化的内容写的不太好,图好像也有问题,时间紧,读者可以读其他关于这部分的内容。
1.3有符号数的补码乘法
在有符号数的补码乘法运算中,我们需要将被乘数和乘数先转化为补码进行乘法运算。运算过程中的所有数据均以补码形式呈现。
符号位也参加运算,在运算过程中要考虑符号位乘上被乘数之后的部分积是正数还是负数。
那么在此基础上,在手动计算时可以将有符号数的乘法运算分为以下四种情况:四位补码 a*b,结果为8位
-
1、a与b均为正数
例:a=5 b=3
a补=0101
b补=0011
直接相乘,然后用最高位补齐8位**(标蓝色的为扩展的符号位),再相加。又因为正数的补码就是其本身**,所以得到结果00001111,化为十进制就是15。注意这里是符号扩展,对应的部分积的那一行的符号位是多少就补什么。

-
2、a为正数,b为负数
例:a=5 b=-3
a补=0101
b补=1101
注意看标红的5个数字,本应该得到0101四位数,再按照扩展符号位的做法,得到00101五位数。但由于b的符号位为1(即b为负数),那么我们需要将得到的00101这五位数,均按位取反再加1,这样就能得到标红的11011了。我们需要把乘数的符号位数1当"-1"来用,需要写出被乘数相反数的补码。
相加得到结果11110001,此时是补码,
再求其原码得10001111,化为十进制为-15。

-
3、a为负数,b为正数
例:a=-3 b=5
a补=1101
b补=0101
乘数的符号位如果是0的话,就当正常的0来用就完了。

-
4、a与b均为负数
例:a=-5 b=-3
a补=1011
b补=1101
相加可以得到已经溢出的结果,只取其低八位,得到00001111,正数的原码等于补码,所以化为十进制得15。

补码乘法的运算需要注意的有两点,记得高位是符号位扩展以及乘数如果是负数的话,符号位1相乘后被乘数应该是被乘数的负数,即被乘数的全部位数取反+1
以上是手动计算补码乘法的过程。
计算机一般采用Booth算法(补码一位乘法)进行补码乘法运算,采用相加和相减操作计算补码数据的乘积。Booth算法及其电路逻辑后续进行讲解。
大概先写这些吧,今天的博客就先写到这,谢谢您的观看。