文章目录
摘要
本周围绕 Goodfellow 等提出的 FGSM 经典论文开展学习,重点梳理其研究背景、国内外研究现状与不足。论文指出对抗样本并非源于深度网络过度非线性,而主要由高维空间下的线性累积效应导致,并在此基础上提出快速生成扰动的 FGSM 方法,为后续对抗训练研究提供理论与方法支撑。
Abstract
This week focused on studying the classic FGSM paper proposed by Goodfellow et al., with emphasis on analyzing its research background, current domestic and international research status, and limitations. The paper demonstrates that adversarial examples do not stem from excessive nonlinearity in deep networks but primarily arise from linear accumulation effects in high-dimensional spaces. Building on this insight, it proposes the FGSM method for rapidly generating perturbations, providing theoretical and methodological foundations for subsequent adversarial training research.
本周学习了论文Explaining and Harnessing Adversarial Examples,初步了解了FGSM。
研究背景
提出背景
随着深度学习模型在图像分类等任务中取得显著进展,神经网络在 MNIST、CIFAR-10 以及 ImageNet 等基准数据集上已表现出较高的分类准确率。已有研究发现,这类模型在面对对抗样本时表现出显著脆弱性,即在原始输入上施加幅度极小、对人类几乎不可感知的扰动,便可能导致模型以较高置信度给出错误预测结果。更为反直觉的是,这种对抗扰动往往能够在不同网络结构和不同训练数据条件下实现跨模型迁移,表明该现象并非源于个别模型或训练不足,而是反映了现有学习模型在高维输入空间中决策机制的内在缺陷。针对早期将对抗样本归因于模型高度非线性或过拟合的解释,Goodfellow 等人从高维空间建模角度重新审视该问题,提出对抗脆弱性与神经网络在实际优化过程中呈现出的近似线性行为密切相关,并在此理论视角下引出了快速生成对抗样本的方法(FGSM),为后续对抗训练和模型鲁棒性研究奠定了基础。
研究现状及不足之处
- 对抗样本现象的提出与验证
早期研究(如 Szegedy 等)首先系统性地揭示了深度神经网络在面对对抗样本时的脆弱性,证明了微小扰动即可导致模型产生高置信度错误预测,并表明该现象在多种模型和数据集上具有普遍性。 - 对抗样本生成方法的局限性
早期对抗样本主要通过约束优化方法(如 box-constrained L-BFGS)生成,该类方法虽然能够稳定构造对抗样本,但计算代价高、生成效率低,难以支撑大规模实验分析或直接嵌入模型训练过程。 - 鲁棒性提升方法效果有限
一些工作尝试通过 dropout、模型集成或生成式建模等方式提升模型鲁棒性,但实验结果表明,这些通用正则化或模型平均策略对缓解对抗脆弱性作用有限,难以从根本上解决问题。 - 理论解释与方法统一性的缺失
总体来看,早期研究在对抗样本产生机理方面缺乏统一且简洁的理论解释,同时在方法层面受限于对抗样本生成效率,尚未形成可扩展、可系统分析的研究框架。
创新点
Explaining and Harnessing Adversarial Examples的创新点主要包括以下几个方面:
提出对抗样本的高维线性成因解释 :
本文突破了早期将对抗样本归因于模型高度非线性或过拟合的直观解释,指出对抗脆弱性本质上源于神经网络在高维输入空间中的近似线性行为。这一理论视角能够统一解释线性模型与深度模型同时存在对抗样本的问题,并合理说明对抗扰动在不同模型之间的迁移性。
提出高效、可扩展的对抗样本生成方法 FGSM :
基于线性解释,作者提出了 Fast Gradient Sign Method(FGSM),仅利用损失函数对输入的梯度符号即可生成对抗样本。相比早期基于约束优化的方法,FGSM 计算代价显著降低,使对抗样本的系统性分析和大规模实验成为可能。
将对抗样本引入训练过程作为有效正则化手段 :
本文首次系统性地将对抗样本用于模型训练,提出基于 FGSM 的对抗训练目标,并实验验证其在提升模型泛化性能和一定程度增强鲁棒性方面的有效性,为后续对抗防御与鲁棒学习研究奠定了基础。
方法论
本文提出了一种基于线性行为的对抗性样本解释方法,并展示了如何利用对抗性训练来提高模型的鲁棒性。
1、线性解释:论文首先解释了线性模型中存在对抗性样本的原因。对于高维空间中的点,由于其精度有限,微小的扰动可以导致输出结果的显著变化。公式如下: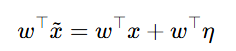
其中,η是扰动向量,w是权重向量,x是输入向量。通过最大化 w⊤η,可以在满足最大范数约束的情况下生成对抗性样本。
2、快速梯度符号法:论文提出了一种快速生成对抗性样本的方法,称为"快速梯度符号法"。该方法通过对当前模型参数的成本函数进行线性化处理,得到一个最优的最大范数约束扰动: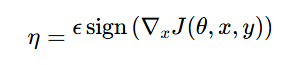
其中,ϵ是一个小的常数,∇xJ(θ,x,y)是成本函数关于输入 x的梯度。

3、对抗性训练:论文进一步探讨了对抗性训练的效果。通过对模型在对抗性样本和干净样本的混合数据上进行训练,可以有效地正则化模型。对抗性训练的目标函数为:

结论
本文通过线性行为的视角解释了对抗性样本的存在原因,并提出了一种快速生成对抗性样本的方法。结果表明,对抗性训练能够提供比dropout更强的正则化效果,显著提高了模型的鲁棒性。论文的贡献在于揭示了对抗性样本的本质,并提出了一种有效的对抗性训练方法,为解决机器学习模型的鲁棒性问题提供了新的思路。
总结
通过对方法论、创新点及结论的学习可知,FGSM 仅需一次梯度计算即可生成对抗样本,显著降低了生成成本并提升攻击效率。论文进一步将对抗样本引入训练过程,提出对抗训练作为一种有效正则化方式,从理论角度揭示了模型鲁棒性问题与高维空间线性行为之间的内在联系,为后续对抗攻击与防御研究提供了重要基础。