对python的再认识-基于数据结构进行-a007-集合-CURD

独好紫罗兰2026-02-10 8:17

Python Set 集合的 CURD

本文聚焦 Python 集合的四大基础操作：增（Create）、查（Read）、删（Delete）、改（Update），包含详细示例与时间复杂度分析。

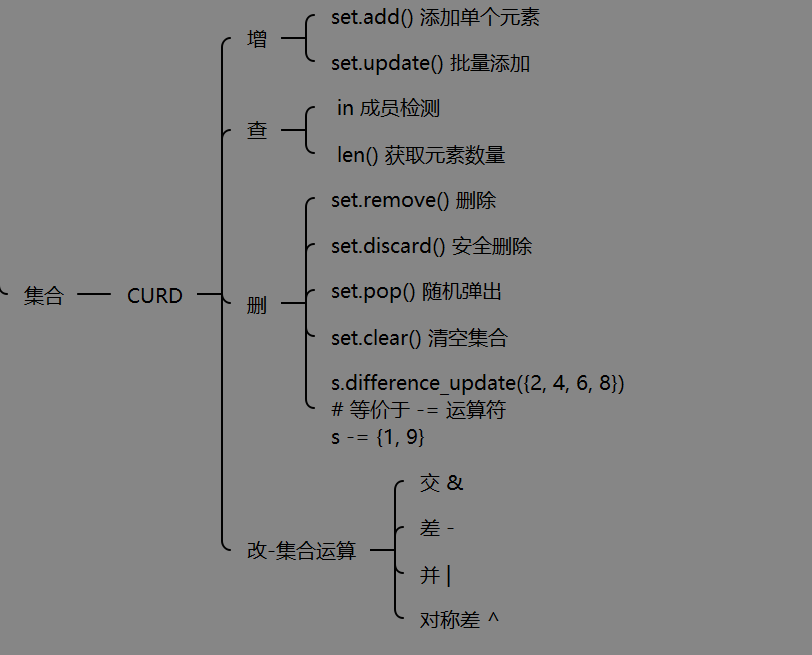
一、增（Create）

1.1 创建集合

python 复制代码 
# 空集合（注意：不能用 {} 创建空集合）
empty = set()
type(empty)  # <class 'set'>

# {} 实际上是空字典
not_empty = {}
type(not_empty)  # <class 'dict'>

# 从可迭代对象创建
nums = set([1, 2, 3, 2, 1])
# {1, 2, 3} - 自动去重

# 从字符串创建
chars = set("hello")
# {'h', 'e', 'l', 'o'} - 去重，顺序不定

# 直接创建（花括号语法）
colors = {"red", "green", "blue"}
# {'red', 'green', 'blue'}

# 创建单元素集合
single = {1,}
# {1}

# 从范围创建
range_set = set(range(5))
# {0, 1, 2, 3, 4}

时间复杂度 ：set(iterable) 为 O(n)，n 为可迭代对象长度

1.2 添加单个元素 add()

python 复制代码 
s = {1, 2, 3}

# 添加元素
s.add(4)
# {1, 2, 3, 4}

# 添加已存在的元素（无效果，不报错）
s.add(3)
# {1, 2, 3, 4}

# 添加不同类型
s.add("hello")
s.add((1, 2))
s.add(3.14)
# {1, 2, 3, 4, 'hello', (1, 2), 3.14}

# ⚠️ 无法添加不可哈希元素
# s.add([1, 2])  # TypeError: unhashable type: 'list'
# s.add({1, 2})   # TypeError: unhashable type: 'set'

时间复杂度 ：add(x) 为 O(1)（平均情况）

1.3 批量添加 update()

python 复制代码 
s = {1, 2, 3}

# 添加列表中的元素
s.update([4, 5, 6])
# {1, 2, 3, 4, 5, 6}

# 添加另一个集合
s.update({7, 8, 9})
# {1, 2, 3, 4, 5, 6, 7, 8, 9}

# 添加字符串（逐字符添加）
s.update("abc")
# {1, 2, 3, 4, 5, 6, 7, 8, 9, 'a', 'b', 'c'}

# 添加元组
s.update((10, 11))
# {1, 2, 3, 4, 5, 6, 7, 8, 9, 'a', 'b', 'c', 10, 11}

# 添加范围
s.update(range(12, 15))
# {1, 2, 3, 4, 5, 6, 7, 8, 9, 'a', 'b', 'c', 10, 11, 12, 13, 14}

# update 等价于 |= 运算符
s |= {15, 16}
# {1, 2, 3, 4, 5, 6, 7, 8, 9, 'a', 'b', 'c', 10, 11, 12, 13, 14, 15, 16}

时间复杂度 ：update(iter) 为 O(k)，k 为添加的元素数量

二、查（Read）

2.1 成员检测 in

python 复制代码 
s = {"apple", "banana", "cherry"}

# in 运算符
"apple" in s    # True
"grape" in s    # False

# not in 运算符
"orange" not in s  # True

# 检测数字
nums = {1, 2, 3, 4, 5}
3 in nums       # True
10 in nums      # False

# 检测元组（元组可哈希）
points = {(0, 0), (1, 1), (2, 2)}
(1, 1) in points   # True
(3, 3) in points   # False

时间复杂度 ：x in s 为 O(1)（平均情况）

2.2 获取元素数量 len()

python 复制代码 
s = {1, 2, 3, 4, 5}

# len() 函数
len(s)  # 5

# 空集合
len(set())  # 0

# 去重后的数量
lst = [1, 2, 2, 3, 3, 3]
len(set(lst))  # 3

时间复杂度 ：len(s) 为 O(1)

2.3 遍历集合

python 复制代码 
s = {"a", "b", "c", "d"}

# for 循环遍历
for item in s:
    print(item)
# 注意：集合无序，输出顺序不确定

# 使用 enumerate 获取索引
for i, item in enumerate(s):
    print(f"{i}: {item}")
# 0: a
# 1: b
# 2: c
# 3: d
# （顺序可能不同）

# 遍历数字集合
nums = {10, 20, 30, 40, 50}
for num in nums:
    print(num * 2)
# 20, 40, 60, 80, 100（顺序可能不同）

时间复杂度 ：遍历为 O(n)，n 为集合大小

2.4 检查集合关系

python 复制代码 
set_a = {1, 2, 3}
set_b = {1, 2, 3, 4, 5}
set_c = {1, 2}

# issubset(): 是否子集
set_c.issubset(set_a)  # True
set_c.issubset(set_b)  # True

# <= 运算符：子集（包含自身）
set_c <= set_a  # True
set_a <= set_a  # True

# < 运算符：真子集（不包含自身）
set_c < set_a  # True
set_a < set_a  # False

# issuperset(): 是否超集
set_b.issuperset(set_a)  # True
set_a.issuperset(set_c)  # True

# >= 运算符：超集（包含自身）
set_b >= set_a  # True
set_a >= set_a  # True

# > 运算符：真超集（不包含自身）
set_b > set_a  # True
set_a > set_a  # False

# isdisjoint(): 是否无交集
{1, 2}.isdisjoint({3, 4})  # True
{1, 2}.isdisjoint({2, 3})  # False

时间复杂度 ：关系检查为 O(min(len(s1), len(s2)))

2.5 复制集合

python 复制代码 
s = {1, 2, 3, 4, 5}

# copy() 方法：浅拷贝
s_copy = s.copy()
# {1, 2, 3, 4, 5}

# 修改原集合不影响副本
s.add(6)
print(s)      # {1, 2, 3, 4, 5, 6}
print(s_copy) # {1, 2, 3, 4, 5}

# 等价于 set() 构造函数
s_copy2 = set(s)

时间复杂度 ：copy() 为 O(n)

三、删（Delete）

3.1 删除指定元素 remove()

python 复制代码 
s = {1, 2, 3, 4, 5}

# 删除元素
s.remove(3)
# {1, 2, 4, 5}

# 删除多个
s.remove(1)
s.remove(5)
# {2, 4}

# ⚠️ 元素不存在时抛出 KeyError
# s.remove(10)  # KeyError: 10

# 安全删除：先检查
if 10 in s:
    s.remove(10)
else:
    print("10 不在集合中")

时间复杂度 ：remove(x) 为 O(1)（元素存在时）

3.2 安全删除 discard()

python 复制代码 
s = {1, 2, 3, 4, 5}

# 删除存在的元素
s.discard(3)
# {1, 2, 4, 5}

# 删除不存在的元素（不报错）
s.discard(10)
# {1, 2, 4, 5}

# 连续删除
s.discard(1)
s.discard(2)
s.discard(100)  # 不存在，也不报错
# {4, 5}

时间复杂度 ：discard(x) 为 O(1)

3.3 删除并返回 pop()

python 复制代码 
s = {1, 2, 3, 4, 5}

# 删除并返回任意元素
element = s.pop()
print(element)  # 可能是 1、2、3、4、5 中的任意一个
print(s)        # 剩余 4 个元素

# 连续弹出
while s:
    elem = s.pop()
    print(f"弹出: {elem}, 剩余: {s}")

# 空集合调用 pop 抛出 KeyError
# set().pop()  # KeyError: pop from an empty set

注意 ：集合无序，pop() 删除的是"任意"元素，不是特定位置

时间复杂度 ：pop() 为 O(1)

3.4 清空集合 clear()

python 复制代码 
s = {1, 2, 3, 4, 5}

# 清空所有元素
s.clear()
print(s)  # set()

# 验证清空后为空
len(s)  # 0

# 重新赋值
s = {1, 2, 3}
s.clear()
s  # set()

时间复杂度 ：clear() 为 O(1)

3.5 删除多个元素

python 复制代码 
s = {1, 2, 3, 4, 5, 6, 7, 8, 9}

# difference_update(): 删除多个元素
s.difference_update({2, 4, 6, 8})
# {1, 3, 5, 7, 9}

# 等价于 -= 运算符
s -= {1, 9}
# {3, 5, 7}

# 保留指定元素（删除不在指定集合中的元素）
s.intersection_update({3, 4, 5})
# {3, 5}

# 保留奇数
odd_set = {1, 3, 5, 7, 9}
s = {1, 2, 3, 4, 5, 6, 7, 8, 9}
s.intersection_update(odd_set)
# {1, 3, 5, 7, 9}

时间复杂度 ：批量删除为 O(len(s_to_remove))

四、改（Update）

集合本身是无序的，没有"修改特定位置元素"的概念。

但可以通过"删除+添加"的方式改变集合内容：

4.1 删除旧值，添加新值

python 复制代码 
s = {1, 2, 3, 4, 5}

# 方式：先删除，再添加
s.discard(3)
s.add(30)
# {1, 2, 4, 5, 30}

# 替换多个值
s.discard(1)
s.discard(2)
s.add(10)
s.add(20)
# {4, 5, 30, 10, 20}

4.2 使用集合运算修改

python 复制代码 
s = {1, 2, 3, 4, 5}

# 并集：添加多个元素
s = s | {10, 20, 30}
# {1, 2, 3, 4, 5, 10, 20, 30}

# 交集：只保留指定元素
s = s & {2, 4, 6, 8}
# {2, 4}

# 差集：删除指定元素
s = s - {4}
# {2}

# 对称差：保留不共有的元素
s = s ^ {2, 3, 4}
# {3, 4}

4.3 原地修改运算符

python 复制代码 
a = {1, 2, 3}
b = {3, 4, 5}

# 原地并集（修改 a）
a |= b
print(a)  # {1, 2, 3, 4, 5}

# 原地交集
a &= {2, 4, 6}
print(a)  # {2, 4}

# 原地差集
a -= {4}
print(a)  # {2}

# 原地对称差
a ^= {2, 3, 4}
print(a)  # {3, 4}

五、集合运算（交并差补）

5.1 并集（Union）

python 复制代码 
a = {1, 2, 3}
b = {3, 4, 5}
c = {5, 6, 7}

# union() 方法
result = a.union(b)
# {1, 2, 3, 4, 5}

# | 运算符
result = a | b
# {1, 2, 3, 4, 5}

# 多个集合的并集
result = a | b | c
# {1, 2, 3, 4, 5, 6, 7}

result = a.union(b, c)
# {1, 2, 3, 4, 5, 6, 7}

时间复杂度：O(len(a) + len(b))

5.2 交集（Intersection）

python 复制代码 
a = {1, 2, 3, 4}
b = {3, 4, 5, 6}
c = {4, 5, 6}

# intersection() 方法
result = a.intersection(b)
# {3, 4}

# & 运算符
result = a & b
# {3, 4}

# 多个集合的交集
result = a & b & c
# {4}

result = a.intersection(b, c)
# {4}

时间复杂度：O(min(len(a), len(b)))

5.3 差集（Difference）

python 复制代码 
a = {1, 2, 3, 4, 5}
b = {4, 5, 6, 7}

# difference() 方法：a 有但 b 没有的
result = a.difference(b)
# {1, 2, 3}

# - 运算符
result = a - b
# {1, 2, 3}

# 反向差集：b 有但 a 没有的
result = b - a
# {6, 7}

# ⚠️ 差集不满足交换律
print(a - b == b - a)  # False（通常）

时间复杂度：O(len(a))

5.4 对称差集（Symmetric Difference）

什么是对称差？

对称差 ：返回只在一个集合中出现的元素，即"非共有"元素。

复制代码 
图解示意：

集合 A:        ████████░░░░░░
集合 B:        ░░░░░░████████
                ────────
并集 (A | B):  ██████████████  (所有元素)
交集 (A & B):  ░░░░░░░░░░░░░░░  (共有元素)
对称差 (A ^ B): ████████░░░████  (只在一个集合中的)
                ──────── ────
基础用法
python 复制代码 
a = {1, 2, 3, 4}
b = {3, 4, 5, 6}

# symmetric_difference() 方法
result = a.symmetric_difference(b)
# {1, 2, 5, 6}
# 解释：1,2 只在 a 中；5,6 只在 b 中；3,4 在两者中（被排除）

# ^ 运算符（更简洁）
result = a ^ b
# {1, 2, 5, 6}
与其他运算对比
python 复制代码 
a = {1, 2, 3, 4}
b = {3, 4, 5, 6}

print(f"A:     {a}")  # {1, 2, 3, 4}
print(f"B:     {b}")  # {3, 4, 5, 6}

print(f"并集:   {a | b}")  # {1, 2, 3, 4, 5, 6} - 所有元素
print(f"交集:   {a & b}")  # {3, 4} - 共有元素
print(f"差集:   {a - b}")  # {1, 2} - a 有 b 没有
print(f"差集:   {b - a}")  # {5, 6} - b 有 a 没有
print(f"对称差: {a ^ b}")  # {1, 2, 5, 6} - 只在一个集合中
等价表达式
python 复制代码 
# 对称差 = 并集 - 交集
result = (a | b) - (a & b)
# {1, 2, 5, 6}

# 对称差 = (a-b) 的并集 (b-a)
result = (a - b) | (b - a)
# {1, 2, 5, 6}
实际应用场景
python 复制代码 
# 1. 找出变化：比较新旧版本
old_version = {"a", "b", "c", "d"}
new_version = {"b", "c", "e", "f"}

# 所有变化的项（新增+删除）
changed = old_version ^ new_version
# {'a', 'd', 'e', 'f'}
# a, d 是删除的；e, f 是新增的

# 2. 找出独有元素
group_a = {"苹果", "香蕉", "橙子"}
group_b = {"香蕉", "葡萄", "西瓜"}

# 只在一个组中出现的水果
exclusive = group_a ^ group_b
# {'苹果', '橙子', '葡萄', '西瓜'}
# 香蕉在两组都有，所以不在结果中

# 3. 比较两个集合的差异
set1 = {1, 2, 3, 4, 5}
set2 = {4, 5, 6, 7, 8}

# 找出不同的元素
different = set1 ^ set2
# {1, 2, 3, 6, 7, 8}

# 4. 多个集合的对称差
a = {1, 2}
b = {2, 3}
c = {3, 4}

# 链式对称差
result = a ^ b ^ c
# {1, 4}
# 解释：出现奇数次的元素保留，出现偶数次的去除
# 1 出现 1 次 → 保留
# 2 出现 2 次 → 去除
# 3 出现 2 次 → 去除
# 4 出现 1 次 → 保留
原地对称差
python 复制代码 
a = {1, 2, 3, 4}

# 原地修改 a
a ^= {3, 4, 5, 6}
# a: {1, 2, 5, 6}

# 等价于
a.symmetric_difference_update({3, 4, 5, 6})

时间复杂度：O(len(a) + len(b))

5.5 集合运算汇总

运算 方法 运算符 描述 返回新集合 原地运算符
并集 union() ` ` (竖线) 两集合所有元素 ✅
交集 intersection() & (且号) 两集合共有的元素 ✅ &=
差集 difference() - (减号) a 有但 b 没有的 ✅ -=
对称差 symmetric_difference() ^ (脱字符) 只在一个集合中的 ✅ ^=

运算符说明：

  • | 或 |：并集（键盘上 Enter 键上方的那个键）
  • &：交集（Shift + 7）
  • ^：对称差（Shift + 6）
  • -：差集（减号）
python 复制代码 
# 快速示例
a = {1, 2}
b = {2, 3}

a | b   # {1, 2, 3} 并集
a & b   # {2}       交集
a - b   # {1}       差集
a ^ b   # {1, 3}    对称差

5.6 原地运算符

python 复制代码 
a = {1, 2, 3}
b = {3, 4, 5}

# 原地并集（a |= b 修改 a，不返回新集合）
a |= b
# a: {1, 2, 3, 4, 5}
# 等价于 a.update(b)

# 原地交集
a &= {2, 4, 6}
# a: {2, 4}
# 等价于 a.intersection_update({2, 4, 6})

# 原地差集
a -= {4}
# a: {2}
# 等价于 a.difference_update({4})

# 原地对称差
a ^= {2, 3, 4}
# a: {3, 4}
# 等价于 a.symmetric_difference_update({2, 3, 4})

优势：原地运算符更高效，不创建新集合

六、操作复杂度总结

操作 方法/运算符 平均复杂度 说明
创建 set(iterable) O(n) n 为可迭代对象长度
添加 add(x) O(1) 均摊
批量添加 update(iter) O(k) k 为添加长度
成员检测 x in s O(1) 平均
长度 len(s) O(1)
删除 remove(x) O(1) 元素存在时
安全删除 discard(x) O(1)
弹出 pop() O(1) 删除任意元素
清空 clear() O(1)
复制 copy() O(n) n 为集合大小
遍历 for x in s O(n) n 为集合大小
并集 `s1 s2` O(m+n)
交集 s1 & s2 O(min(m,n)) 遍历较小集合
差集 s1 - s2 O(m) m 为 s1 长度
对称差 s1 ^ s2 O(m+n) m, n 为两集合长度
关系检查 issubset/issuperset O(min(m,n)) 子集/超集检查

七、总结

操作类别 方法/运算符 要点
创建 set(), {} set() 创建空集合，{} 创建空字典
添加 add(), update() add() 单个 O(1)，update() 批量 O(k)
删除 remove(), discard(), pop(), clear() remove() 元素不存在报错，discard() 不报错
查询 in, len(), 遍历 in 检测 O(1)，len() O(1)
关系 issubset(), issuperset(), isdisjoint() 子集/超集/无交集判断
并集 ` , union()`
交集 &, intersection() 两集合共有元素
差集 -, difference() a 有 b 没有
对称差 ^, symmetric_difference() 只在一个集合中
原地运算 ` =, &=, -=, ^=`
相关推荐
YJlio8 小时前
1.7 通过 Sysinternals Live 在线运行工具：不下载也能用的“云端工具箱”
c语言·网络·python·数码相机·ios·django·iphone
l1t9 小时前
在wsl的python 3.14.3容器中使用databend包
开发语言·数据库·python·databend
青云计划9 小时前
知光项目知文发布模块
java·后端·spring·mybatis
赶路人儿9 小时前
Jsoniter（java版本）使用介绍
java·开发语言
2013编程爱好者9 小时前
【C++】树的基础
数据结构·二叉树·树·二叉树的遍历
NEXT069 小时前
二叉搜索树（BST）
前端·数据结构·面试
化学在逃硬闯CS9 小时前
Leetcode1382. 将二叉搜索树变平衡
数据结构·算法
山塘小鱼儿10 小时前
本地Ollama+Agent+LangGraph+LangSmith运行
python·langchain·ollama·langgraph·langsimth
探路者继续奋斗10 小时前
IDD意图驱动开发之意图规格说明书
java·规格说明书·开发规范·意图驱动开发·idd
热门推荐
01GitHub 镜像站点02Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services03openclaw配置教程（linux+局域网ollama）04UV安装并设置国内源05Linux下V2Ray安装配置指南06openclaw使用nginx反代部署过程 与disconnected (1008): pairing required解决07AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南08【Linux操作系统12】Git版本控制与GDB调试：从入门到实践09简单模板笔记10基于MATLAB的Copula对数似然值计算与参数验证