C语言之雷达安装（贪心算法——区间覆盖）

题目描述

假设海岸线是一条无限延伸的直线。它的一侧是陆地，另一侧是海洋。每一座小岛是在海面上的一个点。雷达必须安装在陆地上（包括海岸线），并且每个雷达都有相同的扫描范围 d。你的任务是建立尽量少的雷达站，使所有小岛都在扫描范围之内。

数据使用笛卡尔坐标系，定义海岸线为 x 轴。在 x 轴上方为海洋，下方为陆地。

输入格式

第一行包括 2 个整数 n 和 d，n 是岛屿数目，d 是雷达扫描范围。

接下来 n 行，每行两个整数，为岛屿坐标。

输出格式

一个整数表示最少需要的雷达数目，若不可能覆盖所有岛屿，输出 -1。

输入

复制代码

输出

复制代码

说明/提示

样例 1 解释

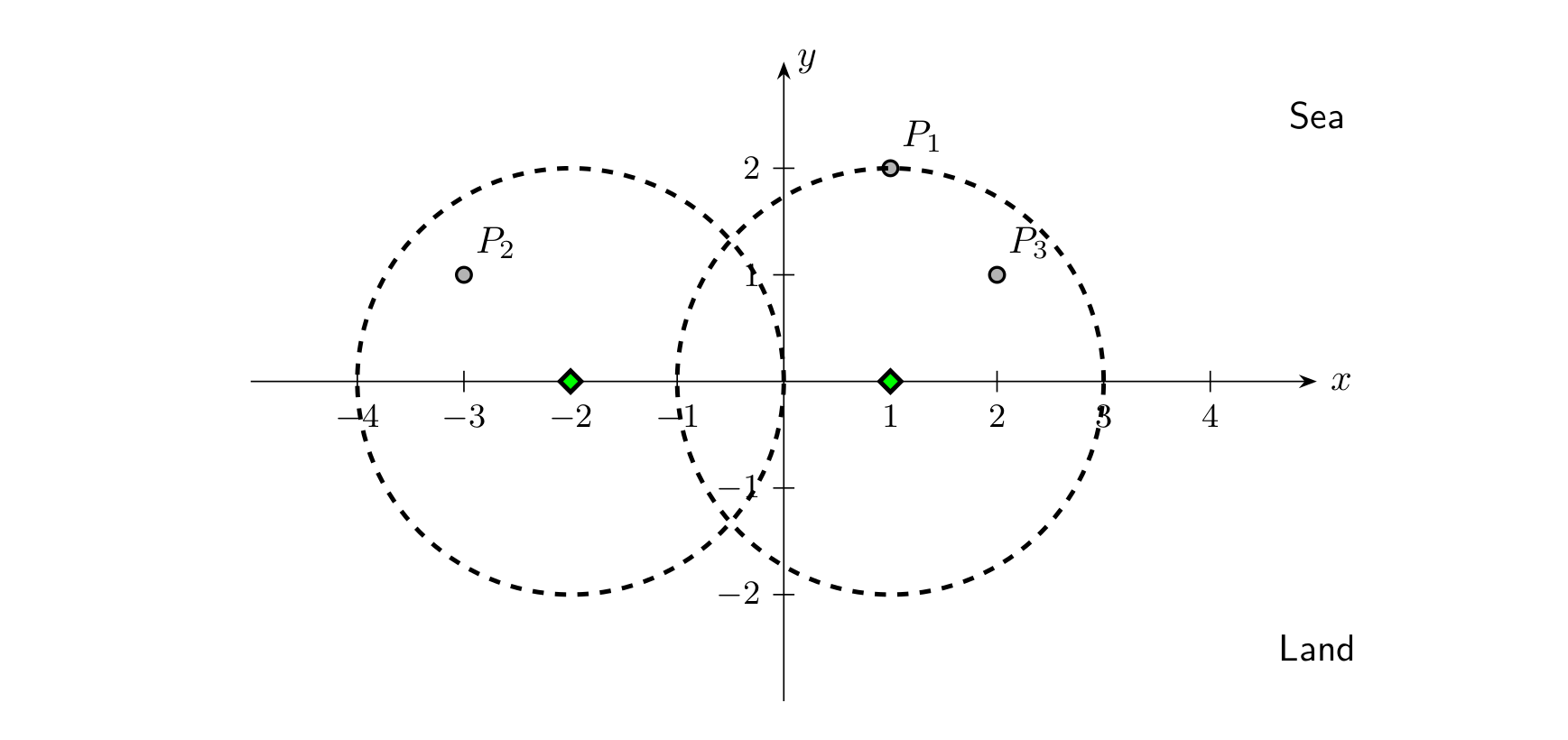
数据范围

对于全部数据，n≤1000，d≤2×10^4，∣xi∣≤2×10^6，0≤yi≤2×10^4。

代码：

cs 复制代码

#include <stdio.h>
#include <math.h>

#define MAXN 1010

typedef struct {
    double l, r;
} Node;

int n;
double d;
double x[MAXN], y[MAXN];
Node a[MAXN];

int main() {
    scanf("%d %lf", &n, &d);
    
    for (int i = 0; i < n; i++) {
        scanf("%lf %lf", &x[i], &y[i]);
        
        // 判断无解情况
        if (y[i] > d) {
            printf("-1\n");
            return 0;
        }
        
        // 计算雷达可覆盖区间
        double dist = sqrt(d * d - y[i] * y[i]);
        a[i].l = x[i] - dist;
        a[i].r = x[i] + dist;
    }
    
    // 使用冒泡排序按区间右端点排序（不使用qsort指针）
    for (int i = 0; i < n - 1; i++) {
        for (int j = 0; j < n - i - 1; j++) {
            if (a[j].r > a[j + 1].r) {
                // 交换两个结构体
                Node temp = a[j];
                a[j] = a[j + 1];
                a[j + 1] = temp;
                
                // 同时也交换对应的x, y数组元素以保持一致（如果需要的话）
                double temp_x = x[j];
                double temp_y = y[j];
                x[j] = x[j + 1];
                y[j] = y[j + 1];
                x[j + 1] = temp_x;
                y[j + 1] = temp_y;
            }
        }
    }
    
    int ans = 0;
    double last_radar = 0;
    
    for (int i = 0; i < n; i++) {
        if (i == 0) {
            last_radar = a[i].r;
            ans++; // 把第一个雷达放置于第一个区间的右端点
        } else if (last_radar >= a[i].l) {
            continue; // 如果当前岛屿可被覆盖，就不放雷达
        } else {
            last_radar = a[i].r;
            ans++; // 否则放置一个新的雷达
        }
    }
    
    printf("%d\n", ans);
    return 0;
}

上述代码整体思路：

利用的是贪心算法------区间覆盖。

首先明确，因为岛屿都是在海上的，而雷达是只能在陆地上的，所以要求最少雷达数，那就是当雷达在海岸线上时，是最优选择。所以只要岛屿的横纵坐标大于雷达扫描范围d，就不可能覆盖这个岛屿，直接无解。但上述只用纵坐标大于d即可，下面用公式讲述......

先计算如果要覆盖这个岛屿，那么雷达可以安装的范围，也就是求最大值和最小值，只要雷达在这个范围内,(包括边界)肯定就覆盖这个岛屿。有3个岛屿，所以可以求出三个边界。因为要求最小雷达数，所以将右边界进行升序排列。将第一个雷达放在排序后的第一个的右边界上，这样才能保证第一个雷达尽可能覆盖下一个岛屿；然后判断排序后的第二个范围的左边界和第一个的右边界是否有重合位置，如果有重合，则说明第一个雷达在第二个范围内，肯定可以覆盖第二个岛屿，那就不用再添加雷达，但如果没有重合，则说明第一个雷达不能覆盖第二个岛屿，肯定就要再添加一个雷达，这个要添加的肯定也要放在第二个范围的右边界。继续按上述循环不变，完成所有岛屿的遍历......

怎么计算雷达可覆盖范围呢？

double dist = sqrt(d * d - y[i] * y[i]);

a[i].l = x[i] - dist;

a[i].r = x[i] + dist;

雷达：必须安装在x轴上，位置为 (radar_x, 0)
岛屿：位置为 (x[i], y[i])，其中 y[i] > 0（在x轴上方）
雷达覆盖半径：d

雷达覆盖岛屿的条件是：岛屿到雷达的距离 ≤ 雷达半径d。每个岛屿对应一个雷达覆盖范围。

复制代码

√[(radar_x - x[i])² + (0 - y[i])²] ≤ d

两边平方：(radar_x - x[i])² + y[i]² ≤ d²→(radar_x - x[i])² ≤ d² - y[i]²

由于 (radar_x - x[i])² ≥ 0，所以要求：d² - y[i]² ≥ 0 => d ≥ y[i]。这就是上面为什么只需要纵坐标大于d的原因。

复制代码

|radar_x - x[i]| ≤ √(d² - y[i]²)→x[i] - √(d² - y[i]²) ≤ radar_x ≤ x[i] + √(d² - y[i]²)

上述就是雷达覆盖范围。因为左右两边几乎一样，最好用变量代替，否则特别麻烦。

复制代码

      岛屿(x[i], y[i])
       /|
      / |
  d  /  | y[i]
    /   |
   /    |
雷达位置  dist = √(d² - y[i]²)
(在x轴上)