机器学习：拟合、欠拟合与过拟合的关系

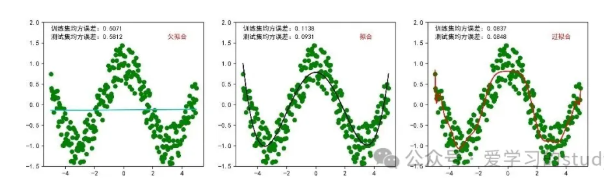
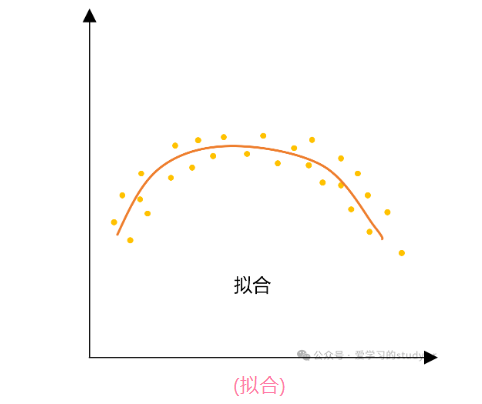
在机器学习模型的学习过程中，若模型能够准确地捕捉训练数据的模式，并且在未见过的新数据（测试数据）上也有良好的表现，那么模型就具有良好的泛化能力（拟合）

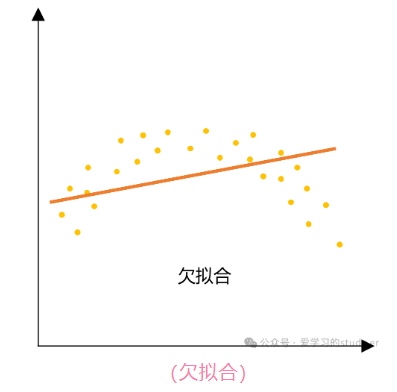
欠拟合(Underfitting): 是指模型在训练数据上表现不佳，无法很好地捕捉数据中的规律。这样的模型不仅在训练集上表现不好，在测试集上也同样表现差。

数据角度：输入特征不充分，或者特征选择不恰当，导致模型无法充分学习数据的模式
模型自身角度：模型过于简单，无法捕捉数据中的复杂关系，也就是说模型复杂度不行，过于简单
训练的角度：训练过程中的次数太少，模型无法充分学习数据规律
超参数的角度：超参数的设置也影响着模型的学习收敛，使用交叉验证or贝叶斯优化进行参数搜索

调试方案：

（1）从数据入手：构造更多特征数据or通过特征工程创造更有信息量的特征。
（2）从模型入手：增加模型的复杂度
（3）从训练入手：增加训练轮次，给予模型充分的时间学习数据规律

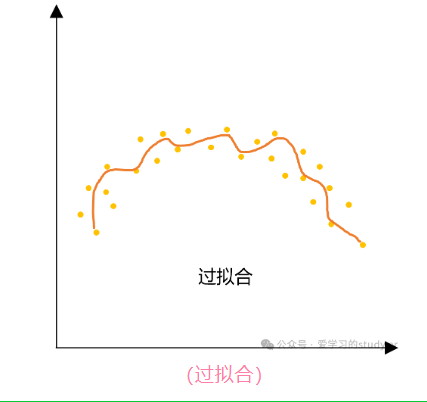
过拟合(Overfitting): 是指模型在训练集上表现得很好，但在测试数据或新数据上表现较差的情况。过拟合的模型对训练数据中的噪声或细节过度敏感，过度学习训练集的性质，从而失去了泛化能力。

数据角度：数据集太小，模型一下子就学会了，记住了太多训练集的细节，导致泛化能力不强
模型自身角度：模型太复杂，参数规模过大
训练的角度：训练的轮次太多，模型学习了噪声等细枝末节的无用信息

调试方案：

（1）从数据入手：增加数据量，或通过数据增强来增加训练数据的多样性
（2）从模型入手：减小模型的复杂程度，缩减参数规模
（3）从训练入手：减小训练轮次，防止模型死记硬背
（4）从正则化入手：引入L1、L2正则化，避免过度拟合数据
（5）从早停策略入手：训练时，当模型的验证损失达到设定阈值，提前停止训练，避免过度拟合训练集

案例：使用常见多项式拟合在[-5,5]区间上拟合函数cos(x)

python 复制代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error # 评估指标

# 全局设置字体，解决中文不显示的bug
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False

def polynomial(x, degree):
    """构成多项式，返回 [x^1,x^2,x^3,...,x^n]"""
    return np.hstack([x**i for i in range(1, degree + 1)])
    
# 构造数据：X在[-5,5]均匀分布，y=cos(X)+噪声
X = np.linspace(-5, 5, 300).reshape(-1, 1)
y = np.cos(X) + np.random.uniform(-0.5, 0.5, 300).reshape(-1, 1)
fig, ax = plt.subplots(1, 3, figsize=(15, 4))
ax[0].plot(X, y, "go")
ax[1].plot(X, y, "go")
ax[2].plot(X, y, "go")
# 划分训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=22)
# 创建线性回归模型
model = LinearRegression()
# 欠拟合，使用原始特征（degree=1，即线性回归）
x_train1 = x_train
x_test1 = x_test
model.fit(x_train1, y_train)  # 模型训练
y_pred1 = model.predict(x_test1)  # 预测
ax[0].plot(np.array([[-5], [5]]), model.predict(np.array([[-5], [5]])), "c")  # 绘制曲线
ax[0].text(-5, 1.6, f"测试集均方误差：{mean_squared_error(y_test, y_pred1):.4f}")
ax[0].text(-5, 1.8, f"训练集均方误差：{mean_squared_error(y_train, model.predict(x_train1)):.4f}")
ax[0].text(3, 1.6, "欠拟合", c='r')
ax[0].set_ylim(-1.5, 2.0)

# 恰好拟合，使用5次多项式特征
x_train2 = polynomial(x_train, 5)
x_test2 = polynomial(x_test, 5)
model.fit(x_train2, y_train)  # 模型训练
y_pred2 = model.predict(x_test2)  # 预测
ax[1].plot(X, model.predict(polynomial(X, 5)), "k")  # 绘制曲线
ax[1].text(-5, 1.6, f"测试集均方误差：{mean_squared_error(y_test, y_pred2):.4f}")
ax[1].text(-5, 1.8, f"训练集均方误差：{mean_squared_error(y_train, model.predict(x_train2)):.4f}")
ax[1].text(3, 1.6, "拟合", c='r')
ax[1].set_ylim(-1.5, 2.0)

# 过拟合
x_train3 = polynomial(x_train, 20)
x_test3 = polynomial(x_test, 20)
model.fit(x_train3, y_train)  # 模型训练
y_pred3 = model.predict(x_test3)  # 预测
ax[2].plot(X, model.predict(polynomial(X, 20)), "r")  # 绘制曲线
ax[2].text(-5, 1.6, f"测试集均方误差：{mean_squared_error(y_test, y_pred3):.4f}")
ax[2].text(-5, 1.8, f"训练集均方误差：{mean_squared_error(y_train, model.predict(x_train3)):.4f}")
ax[2].text(3, 1.6, "过拟合", c='r')
ax[2].set_ylim(-1.5, 2.0)
plt.show()