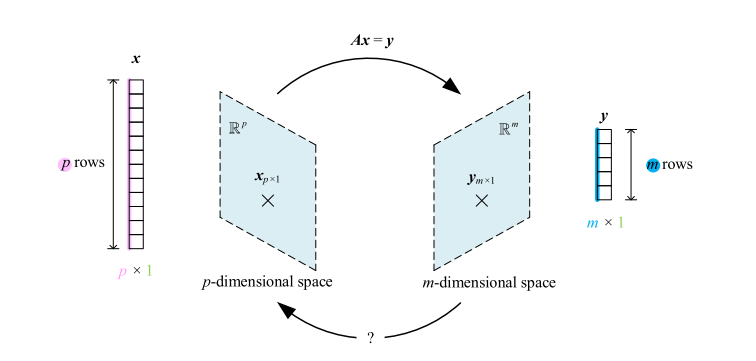
（图1 来自《线性代数不难》）
这张图其实把矩阵乘法的本质 画得很直白：它不是"神秘的算式"，而是一个把向量从一个空间线性映射到另一个空间的规则。
1）先读图：维度在说什么？
-
左边是输入向量 x ：标着 p rows，所以
-
右边是输出向量 y ：标着 m rows，所以
-
中间写着 Ax=y ：说明矩阵 A 必须把
的向量送到
因此 A 的尺寸被"维度匹配"强制确定为：
这就是为什么矩阵乘法要求"内维相等"：(m×p)(p×1)=(m×1)。
2）矩阵乘法的三个等价理解（都对应同一个 y=Ax）
视角 A：行·列（点积）= 输出每一行
把 A 看成由 m 行组成：
那么输出 y 的第 i 个分量就是：
也就是：每一行和 x 做一次点积，得到一个标量；做 m 次得到 m 维的 y。
视角 B：列的线性组合（最直观）
把 A 按列拆开：
把 x 写成分量 ，则
这句话非常关键：
矩阵乘向量 = 用 x 的各个分量当系数，把 A 的各列加权相加。
所以 A 的每一列都像一个"输出方向的基向量/特征图"，x 决定你把这些列混合成什么样的 y。
视角 C：函数/变换：线性映射
图中两块"斜着的平面"写着 和
，强调的是：
-
输入空间的点 x
-
经过 A 这个规则
-
变成输出空间的点 y
而且是"线性"的：满足
这就是为什么矩阵能表示：旋转、缩放、剪切、投影、把 2D 嵌到 3D、把高维压到低维......（取决于 m,p 和 A 的结构）。
3）图里底部那个"？"箭头在暗示什么？
它像是在问：能不能从 y 反推回 x？
-
如果 A 是 方阵 （m=p）且 可逆：就有
-
如果 不是方阵 或 不可逆 ：通常不能唯一反推。这时常见做法是：
-
最小二乘：找一个 x 让 ∥Ax−y∥ 最小
-
伪逆：
-
这就是机器学习/信号处理里"拟合""回归""重建"背后的线性代数版本。
4）一个小数值例子，把图走一遍
让 p=2，m=3（从 映射到
）：
则
-
行·列视角：三行分别点积得到 y1,y2,y3
-
列组合视角：
两种理解算出来完全一致。
矩阵乘法的几何视角
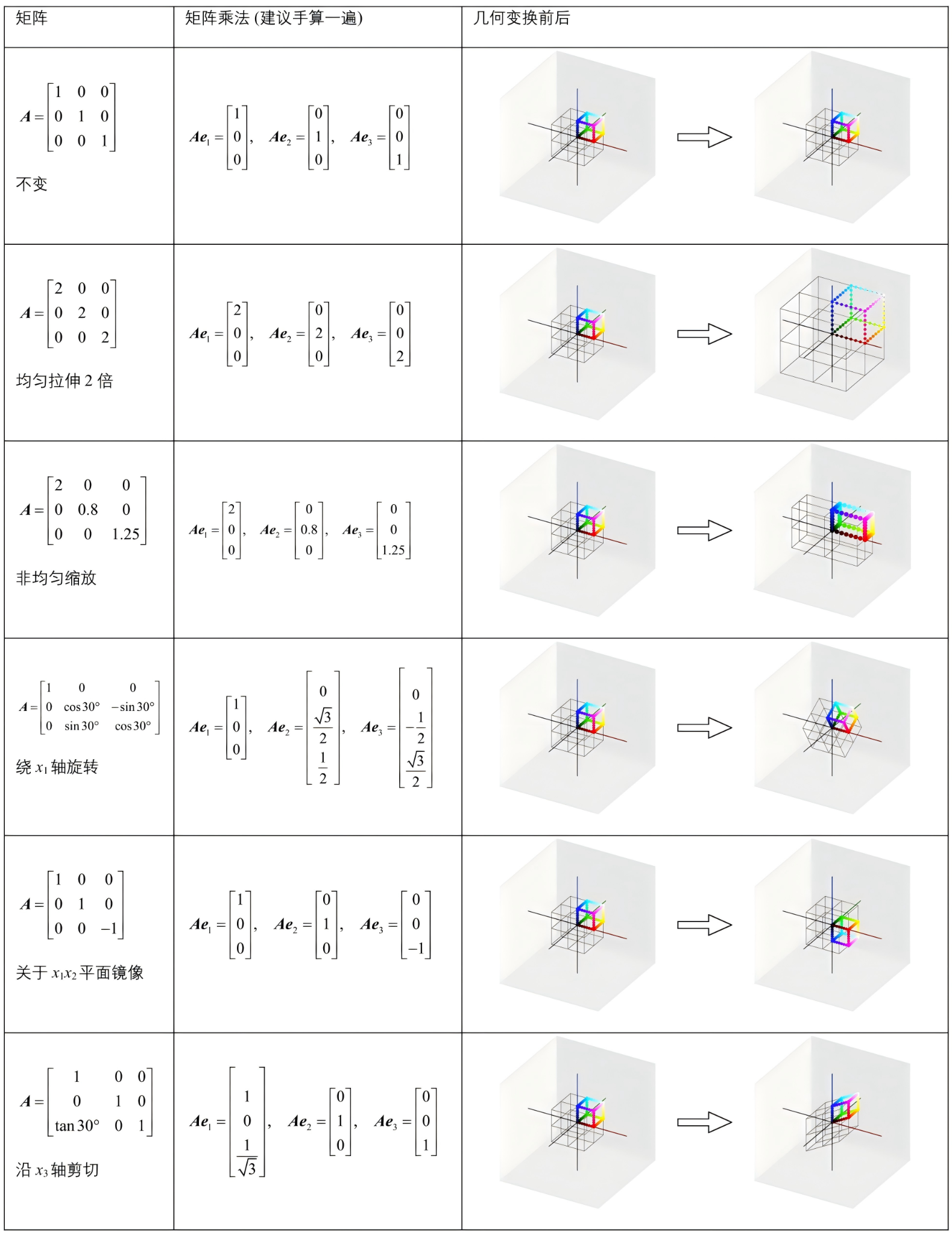
（图2 来自《线性代数不难》）
这张图想表达的核心只有一句话：
矩阵乘法 y=Ax 的几何意义：线性变换把"整个空间里的所有向量/点"一起搬家；而你只要看清楚它把三个基向量 e1,e2,e3 变成了什么，就等于看清了整个变换。
1）为什么"看 "就够了？
在 3D 里任意向量都能写成
由于线性变换满足"可加+可提系数"，
而 正好就是 矩阵 A 的第 i 列：
所以在图中间看到的"建议手算一遍："就是在做这件事：
把坐标轴的三根单位箭头（基向量）变换后的位置算出来，整个空间的形变就定了。
2）几何上到底发生了什么？
可以把左边那个小彩色立方体当成**"单位立方体"**（或者一小块网格）。线性变换会把它变成一个平行六面体：
-
列向量
-
单位立方体的 8 个顶点会被一起送到新位置，所以整体形状被拉伸/旋转/剪切/翻转。
记忆法：列 = 新轴 ，立方体 = 被变形的空间小块。
3）逐行对应图里的 6 种变换
下面每一行都在说："三根基向量被送到哪里" → "几何效果是什么"。
(1) 单位矩阵 ：不变
三根轴方向完全没动，所以立方体不变。
(2) ：均匀拉伸 2 倍
三根轴都变长 2 倍、方向不变，所以是整体放大 。
体积缩放因子是 det(A)=2⋅2⋅2=8：立方体体积变 8 倍。
(3) 对角矩阵 diag(2,0.8,1.25)：非均匀缩放
三根轴分别按不同倍数伸缩 → 长方体拉伸 （各向异性缩放）。
体积缩放 det(A)=2×0.8×1.25=2：体积变 2 倍，但形状比例变了。
(4) 绕 x1 轴旋转（图里是 30∘）
矩阵大致是
它的效果是：
-
-
所以右图看到的是：立方体整体绕 x1 轴转过去，但"长度、角度（正交性）、体积"都保持（旋转矩阵 det=1）。
(5) 关于 x1x2 平面镜像（等价：x3 取反）
这表示：
-
x1,x2 不变
-
x3 方向翻到相反
几何上是上下翻转（镜像）。注意它会改变"朝向"（右手系变左手系），因此 det(A)=−1。
(6) 沿 x3 方向剪切（图里用 tan30∘）
图里是
算基向量：
-
-
几何直觉：不同的 x1 位置，会被额外抬高/压低一些 x3 ，于是立方体被"斜着推"成平行六面体。
这种剪切通常 det(A)=1：体积不变，但角度变了（不再正交）。
4）一眼看懂矩阵几何意义的"快法"
给你一个非常实用的流程（和图中间那列完全一致）：
-
看列向量 ：第 1、2、3 列分别是
-
判断三根新轴：长度（缩放）、方向（旋转/反射）、是否倾斜（剪切）
-
判断体积与朝向：看 det(A)
-
∣det∣>1：体积放大；∣det∣<1：体积缩小
-
det<0：发生镜像（朝向翻转）
-
我们继续把矩阵乘法的几何视角讲得更"能一眼看出来"。
5）同一个 Ax，有两种等价的"几何画法"
(5.1) 列视角（column picture）：看"新坐标轴 / 新基向量"
这是图里用的视角：
-
A 的第 1、2、3 列分别就是
-
它们告诉你：原来坐标轴的单位箭头被变到哪里
-
所以单位立方体会被拉成由这三根向量张成的平行六面体
一句话总结：
列 = 变换后的轴；立方体怎么变形由列决定。
(5.2) 行视角（row picture）：看"输出每个分量怎么测量（投影/点积）"
把 A 写成行：
那么
几何意义是：每一行 都像一个"探针方向"，输出的第 i 个坐标就是把 x 沿这个方向做一次点积（某种测量/投影）。
一句话总结：
行 = 怎么把输入"测成"输出坐标。
这两个视角讲的是同一个 Ax，只是"看法"不同：
-
列视角更像"把空间变形"
-
行视角更像"对输入做测量得到输出"
6）矩阵乘矩阵 BA：为什么是"先 A 后 B"？
这是几何里最关键的一条：
所以 右边先作用：
-
先用 A 把 x 从原空间变到中间形状
-
再用 B 在新形状上继续变
这也是为什么线性变换的"组合"用乘法表示。
更直观的列视角说法：
-
A 的列给出
-
再乘 B：
-
也就是：先把轴变到
所以矩阵乘法不是"乱算"，而是"变换的叠加"。
7）det(A) 的几何意义：体积缩放 + 是否翻面
你已经看到：
-
均匀缩放 2 倍：det=8
-
镜像：det=−1
-
剪切常常：det=1
更通用地：
-
∣det(A)∣ = 体积缩放倍数（3D 是体积，2D 是面积）
-
det(A)>0：保持朝向（右手系还是右手系）
-
det(A)<0：发生镜像，朝向翻转（右手系变左手系）
一个非常实用的"肉眼判断"：
-
三根列向量越"张得开"，∣det∣ 越大
-
三根列向量越"挤到一个平面里"，∣det∣ 越接近 0
-
如果三根列向量共面/共线，det=0：体积被压扁成 0（不可逆）
8）秩（rank）与"压扁"：从 3D 变 2D/1D/0D 的几何解释
秩 = 变换后能留下的维度（输出子空间的维数）。
在 3D 中：
-
rank = 3：立方体变成某个"有体积"的平行六面体（det≠0）
-
rank = 2：立方体被压成一个平行四边形"薄片"（体积 0）
-
rank = 1：压成一条线段
-
rank = 0：全变到原点
从列视角看最直观：
-
rank 就是
-
三列不共面 → rank 3
-
三列共面但不共线 → rank 2
-
三列共线 → rank 1
-
9）当 m≠p：图一那种"从 p 维到 m 维"怎么理解？
这是图1 的延伸。
(9.1) m>p：升维（embedding）
比如 。几何上是：
-
一个 2D 平面被嵌进 3D
-
变换结果仍然只能落在某个 2D 子空间里（rank ≤ 2）
(9.2) m<p：降维（projection / measurement）
比如 。几何上是：
-
你把 3D 点"测量"成 2 个数字（行视角非常贴切）
-
必然丢信息，所以一般不能唯一反推
这也解释了图1 底部那个"？"：
反推需要可逆，但降维或 rank 不满时做不到，只能做最小二乘/伪逆那类"最接近"的逆。
10）把那张表总结成一句"万能口诀"
矩阵乘法的几何本质：把基向量送到新位置（列），从而决定整个空间如何变形；组合变换就是矩阵相乘；体积与翻面由行列式控制；压扁程度由秩控制。