系统参数标定

前言：通过该篇文章，重新梳理，理解系统标定参数的含义，及标定过程

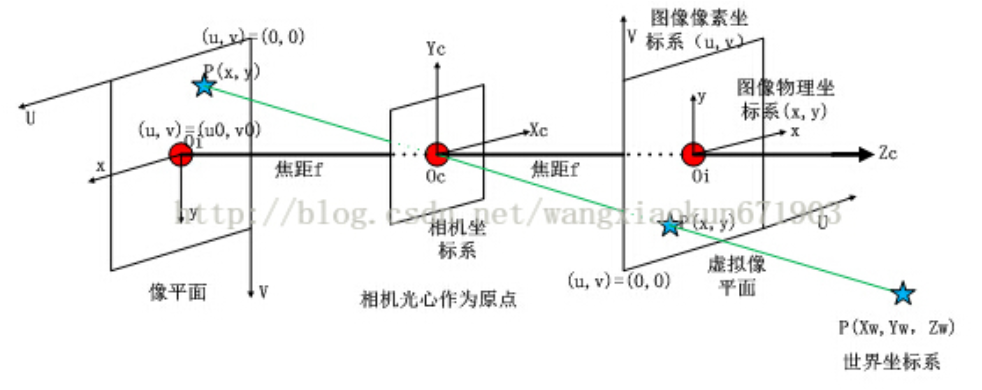
针孔成像模型

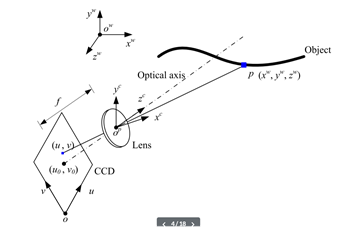
假设空间中物体任意一点在世界坐标系下为p(x,y,z) ，在摄像机成像平面上的投影坐标为 (u,v)，则实际上，这一转换过程可以描述为：

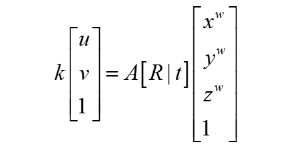
其中：K 为缩放因子； $R\|t$ 表示外部参数：

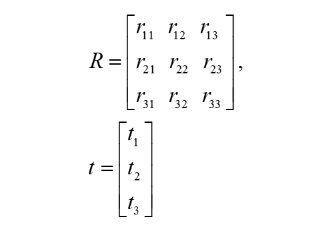
R是一个三行三列的旋转矩阵，而t代表了一个平移向量。它们共同表示了三维世界中点到相机坐标系统中的关系。接着，相机本身的内部参数矩阵A会将坐标映射到相机的二维成像平面上，最终得到世界相应的二维图像坐标。

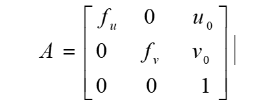其中，fu和 fv分别表示相机在 u 轴和v 轴方向上的有效焦距；(u,v)则是主点坐标，即相机光轴与图像平面的交点。

常见的系统参数标定方法是张正友方法，该方法利用多个不同角度拍摄的棋盘格图像，通过单应性矩阵（Homography Matrix）估计摄像机的内参、外参和畸变参数，并采用非线性优化方法提升精度。

系统标定用来确定系统的内外参数，其中内参描述相机内部属性的参数，包括焦距、主点（光学中心）坐标、畸变系数等。输出值有焦距（fu,fv）,(u,v),径向畸变参数k1,k2,k3；切向畸变系数 p1，p2; 外参描述相机在世界坐标系中的位置和姿态的参数，通常包括旋转矩阵和平移向量。

标定板用来辅助系统标定，通常假设标定点平面z=0;以左上角第一个圆心为世界坐标系原点位置。系统外参确认了相机坐标系与世界坐标系的对应关系，其两个坐标系单位都还是mm。

坐标系转换

% 世界 -> 相机

points_cam = (R * points_world.' + t); % 3×N

从相机坐标系到像素坐标系：

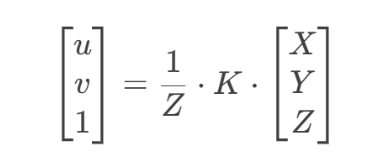
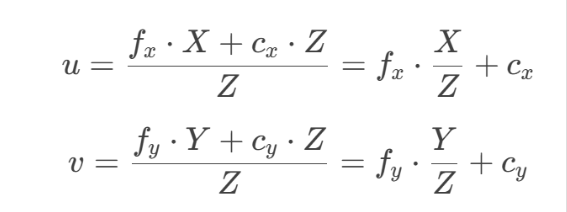
在单目结构光系统中，当已知相机和投影仪在同一世界坐标系外参时，就可以通过下式代码得到两个设备的相对关系矩阵。

matlab 复制代码

% ================== 已知外参 ==================
% 相机外参 (world -> camera)
rvec_cam = [2.1719   , 2.1701 ,  -0.0352];
tvec_cam = [-72.6580;
 -125.2286;
  422.8802];  % mm

% 投影仪外参 (world -> projector)
rvec_proj = [   -2.0823  , -2.1271  ,  0.0308];
tvec_proj = [ -132.9652;
 -231.0133;
  502.7903]; % mm

% ================== 计算旋转矩阵 ==================
R_cam = vision.internal.calibration.rodriguesVectorToMatrix(rvec_cam);
R_proj = vision.internal.calibration.rodriguesVectorToMatrix(rvec_proj);

% ================== 计算 projector w.r.t camera ==================
% R_pc = R_proj * R_cam'
R_pc = R_proj * R_cam';

% T_pc = -R_pc * tvec_cam + tvec_proj
T_pc = -R_pc * tvec_cam + tvec_proj;

% ================== 计算 camera w.r.t projector ==================
% 旋转矩阵取转置
R_cp = R_pc';

% 平移向量逆变换
T_cp = -R_pc' * T_pc;

% Rodrigues 旋转向量
rvec_cp = vision.internal.calibration.rodriguesMatrixToVector(R_cp);

% ================== 输出 ==================
disp('R_ex (camera w.r.t projector):');
disp(R_cp);

disp('T_ex (mm):');
disp(T_cp);

disp('rvec_ex (rad):');
disp(rvec_cp);