PCL 点云匹配 NDT详解

1. NDT 是什么？

Normal Distributions Transform（NDT）是由 Biber & Straßer (2003) 提出的 用于点云配准（scan matching） 的方法。

它是 ICP 的概率版，核心思想是：

将目标点云划分为网格，每个网格估计一个高斯分布，源点云点作为观测输入该高斯分布的概率。通过最大化整体概率来求刚体变换。

2. NDT 数学原理（最重要）

2.1 Step 1：把目标点云分为体素 (Voxel Grid)

每个 voxel（体素）内的点：

2.2 Step 2：使用高斯分布建模每个 voxel

对每个 voxel，我们有：

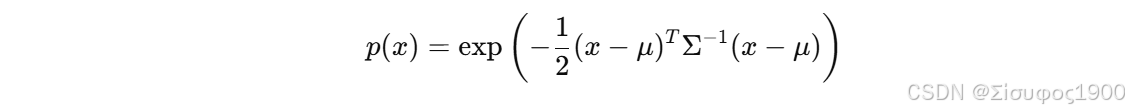
2.3 Step 3：源点云经过变换后最大化目标点云的概率

2.4 Step 4：对刚体变换线性化（LM / Gauss-Newton）

对微扰：

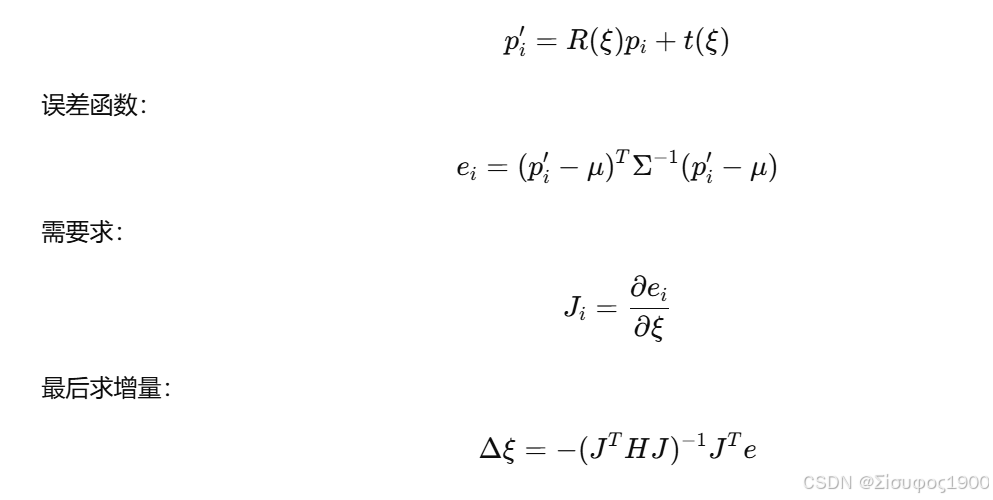
3、MATLAB 完整实现

MATLAB NDT 配准代码

cpp 复制代码

function T = ndt_registration(P, Q, voxel_size, max_iter)
    % P : target point cloud Nx3
    % Q : source point cloud Nx3

    % 1. Voxelization of target cloud
    [voxels, mu, SigmaInv] = ndt_build_model(P, voxel_size);

    T = eye(4);  % initial pose
    
    for iter = 1:max_iter
        R = T(1:3,1:3); 
        t = T(1:3,4);
        
        J = zeros(6,6);
        b = zeros(6,1);

        for i = 1:size(Q,1)
            q = R*Q(i,:)' + t;     % transformed source point
            
            % find voxel ID
            vid = ndt_find_voxel(q, voxel_size);
            if ~isKey(voxels, vid), continue; end
            
            mu_i = mu(vid,:);
            S   = SigmaInv{vid};

            d = q - mu_i';          % residual
            
            e = d' * S * d;         % error
            
            % Jacobian wrt ξ (Lie algebra)
            % dq/dξ = [I, -R*[q]_x]
            Jq = [eye(3), -R*skew(Q(i,:)')];

            Ji = 2 * Jq' * S * d;

            J = J + Ji * Ji';
            b = b + Ji * e;
        end
        
        delta = -J \ b;

        % update pose
        T = expmap_se3(delta) * T;

        if norm(delta) < 1e-5, break; end
    end
end

构建 NDT 体素模型

cpp 复制代码

function [voxels, mu, SigmaInv] = ndt_build_model(P, voxel_size)
    voxels = containers.Map();
    mu = containers.Map();
    SigmaInv = containers.Map();

    % Assign points to voxels
    ids = floor(P / voxel_size);

    for i = 1:size(P,1)
        key = sprintf('%d_%d_%d', ids(i,1), ids(i,2), ids(i,3));
        if ~isKey(voxels, key)
            voxels(key) = [];
        end
        voxels(key) = [voxels(key); P(i,:)];
    end

    % Compute Gaussian per voxel
    keys = voxels.keys;
    for i = 1:length(keys)
        k = keys{i};
        pts = voxels(k);

        m = mean(pts,1);
        C = cov(pts) + 1e-3 * eye(3);
        
        mu(k) = m;
        SigmaInv{k} = inv(C);
    end
end

SE(3) 李代数工具

cpp 复制代码

function S = skew(v)
    S = [   0   -v(3)  v(2)
          v(3)    0   -v(1)
         -v(2)  v(1)    0 ];
end

function T = expmap_se3(xi)
    w = xi(1:3);
    v = xi(4:6);
    theta = norm(w);

    if theta < 1e-8
        R = eye(3);
        V = eye(3);
    else
        wn = w / theta;
        wx = skew(wn);        
        R = eye(3) + sin(theta)*wx + (1-cos(theta))*(wx*wx);
        V = eye(3) + (1-cos(theta))*wx + (theta-sin(theta))*(wx*wx);
    end

    T = eye(4);
    T(1:3,1:3) = R;
    T(1:3,4) = V * v;
end

可视化示例

cpp 复制代码

P = pcread("bun000.ply").Location;
Q = pcread("bun000.ply").Location; % rotated version

T = ndt_registration(P, Q, 0.05, 30);

Q_reg = (T(1:3,1:3)*Q' + T(1:3,4))';

pcshow(P,'b.'); hold on;
pcshow(Q_reg,'r.');
legend("Target","Registered");