R语言两种方法手搓竞争风险模型（1）

竞争风险模型就是指在临床事件中出现和它竞争的结局事件，这是事件会导致原有结局的改变，因此叫做竞争风险模型。比如我们想观察患者肿瘤的复发情况，但是患者在观察期突然车祸死亡，或者因其他疾病死亡，这样我们就观察不到复发情况了，这种情况下不能把缺失数据仅仅当做右删失处理，这样的话会造成数据的估值错误。这是我们应该优先选择竞争风险模型来做数据分析，而不是COX回归。

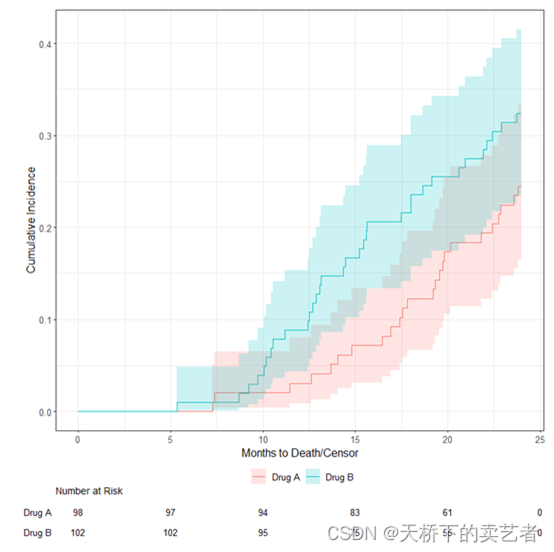
平时咱们进行竞争风险模型分析都是使用R语言的cmprsk包，但是cmprsk包的核心算法是用C++写的，不利于咱们了解竞争风险模型的原理和计算方法，今天我来使用R语言手搓一个竞争风险模型原理，有利于咱们进一步了解竞争风险模型。

竞争风险模型通常有2种主流算法，

第一种是cause-specific hazard（CSH）方法（即通过积分 ∫S(u) dΛk(u)∫S(u)dΛk(u) 计算 CIF）

第二种就是Fine-Gray 模型，是竞争风险分析中估计累积发生率函数（CIF）的另一种主流方法

咱们今天介绍的就是第二种，要是第一种感兴趣的人多，也可以说说。先来看下他的公式

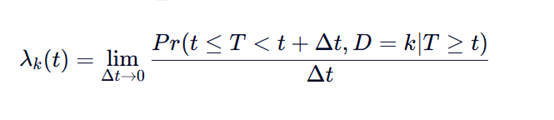
公式有两个大小t, T表示观察到的事件发生时间，t是咱们的时间，.表示在时间 t 时，在尚未发生任何事件的条件下，单位时间内发生第 k 类事件的瞬时风险。

Fine 和 Gray 提出了一种直接对 CIF F_k(t) 进行建模的方法。他们定义了次分布风险函数：

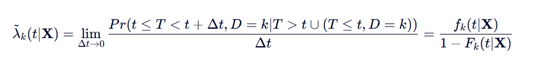
T: 观察到的事件发生时间，fk 是事件的密度函数，分母fk(t|x)，表示"尚未发生事件 k"的概率。这包括了两类人：(1) 真正存活的人 (T > t)，因为还没发生事件；(2) 已经死于其他原因的人 (T ≤ t, D ≠ k)，D就是死亡，k就是本次事件，表示t大于T但是不是死于结局事件，咱们可以看到这一部分的pr也是被保留了。后者被当作"风险集"的一部分保留下来，而不是像标准Cox模型那样将他们移除，即删失。

由上面公式看出，它只关心"活到现在"的人，不区分未来的事件类型。它衡量的是事件 k 的"原始"发生倾向。

模型形式: Fine-Gray模型假设次分布风险满足比例风险假设

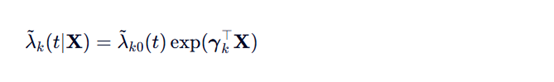
上面公式可以进一步推到为下面公式

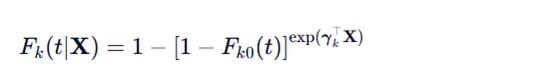
Fk0(t)是f{X}=0的时候的基线CIF

下面咱们来使用R语言手搓一下竞争风险模型，结果和cmprsk包进行比较一下

先导入数据和R包，

r 复制代码

library(survival)
library(cmprsk)
setwd("E:/公众号文章2026年/手搓竞争风险模型")
dat<-read.csv("dat.csv")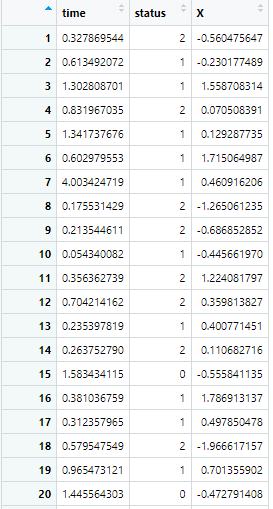

这是一个简单的数据，time是事件，status是结局，x是观察变量，咱们主要是通过这个简单数据了解一下竞争风险模型的分析原理。，这里1为目标事件

首先要把反着来，把删失（就是没有发生事件的结局）作为事件，其他作为删失

r 复制代码

dat$censor_event <- as.numeric(dat$status == 0)  # 1 = censored
km_censor <- survfit(Surv(time, censor_event) ~ 1, data = dat)

这样咱们就构造了一个status == 0的分布数据，提取相关的事件和时间数据

r 复制代码

G_times <- c(0, km_censor$time)
G_surv  <- c(1, km_censor$surv)

构造G（t）函数，在这个函数中，findInterval函数的就是找到当前时间所在G_times时间所在的分布位置

r 复制代码

G_func_safe <- function(t) {
  idx <- findInterval(t, G_times, rightmost.closed = TRUE)  
  idx[idx == length(G_surv)] <- length(G_surv) - 1
  out <- G_surv[idx + 1]
  out
}

接下来需要定义一个对数似然函数

r 复制代码

neg_log_pl_fg <- function(beta, data, G_func) {
  X <- data$X
  time <- data$time
  status <- data$status
  for (k in seq_along(fail_idx)) {
    j <- fail_idx[k]
    t_j <- fail_times[k]
    in_risk <- (time >= t_j) | (status == 2 & time < t_j)
    
    Ti_adj <- pmin(time[in_risk], t_j)
    G_tj <- G_func(t_j)
    weights_ij <- G_tj / G_Ti_adj
    eta_risk <- beta * X[in_risk]
    exp_eta_risk <- exp(eta_risk)
    
    denom <- sum(weights_ij * exp_eta_risk)
    idx_j_in_risk <- which(in_risk)[which((1:n)[in_risk] == j)]
    if (length(idx_j_in_risk) == 0) next
    
    w_j <- weights_ij[idx_j_in_risk]    
    if (denom > 0) {
      loglik <- loglik + log(num / denom)
    }
  }
  
  return(-loglik)  # 返回负对数似然
}

OK，咱们把上面过程打包成一个函数，使用海瑟矩阵来计算，进行分析一下

r 复制代码

cmprsk_crr(data = dat,y="status",x="X",time = "time")

咱们可以看到系数是0.637，标准误是0.08，接下来咱们使用cmprsk包来分析一下

r 复制代码

library(cmprsk)
crr(dat$time,dat$status,cov1 = as.matrix(dat$X),failcode = 1,cencode = 0)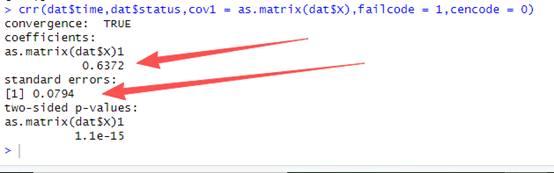

咱们可以看到系数是0.672，标准误是0.0794，和咱们计算的几乎完全一样，说明咱们的计算过程是没有问题的。

如果咱们换个方法，使用第一种方法来计算，也就是cause-specific hazard（CSH）方法，咱们看一下有什么不同，我也用第一种方法写了一个函数（有兴趣的人多我也可以手搓一下）

r 复制代码

cmprsk_hr(dat, time = "time",y =  "status",x="X",weights = "w")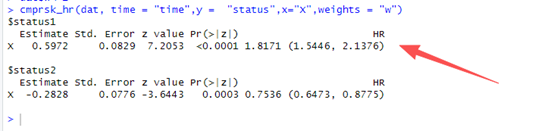

结果看第一个，系数大概是0.6，标准误大概是0.08，在我看来这两种完全不同的算法算出来的结果在方向和系数几乎都是一致了。

OK，本期结束。

最后，提前祝大家新年快乐，合家美满，咱们来年再见。