Kabsch 算法 - 技术栈

1、Kabsch 算法

Kabsch 算法是一种用 SVD 求解两组对应点之间最优旋转矩阵 R 的方法，使它们的均方误差最小。
它是 ICP、结构生物学、机器人学中最常用的刚体对齐算法。

2、应用场景

✔ 1. ICP（Point-to-Point）核心步骤

求 R、t 用来把源点云对齐到目标点云。

✔ 2. 蛋白质结构比对（Kabsch 最早来自生物化学）

对齐两段蛋白质链。

✔ 3. 机器人位姿估计（Hand-Eye, PnP 简化版）

从 A→B 的对应点求最优旋转。

3、问题模型

4、Kabsch 解决步骤（核心：SVD）

Step 1：去中心化（必须）

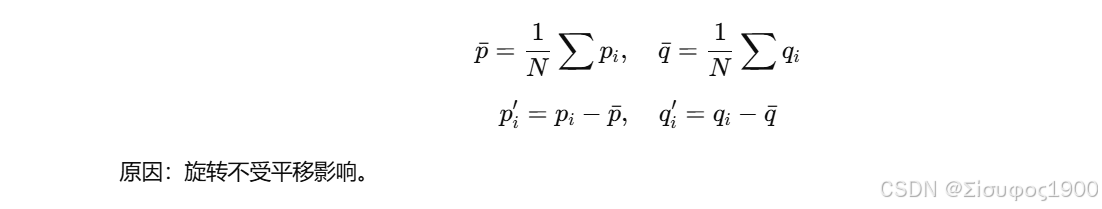
Step 2：构造协方差矩阵

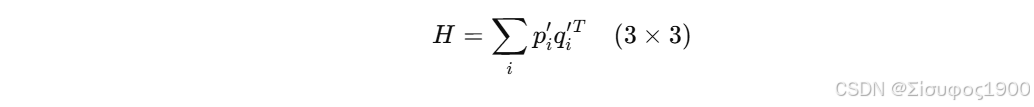
Step 3：SVD 分解

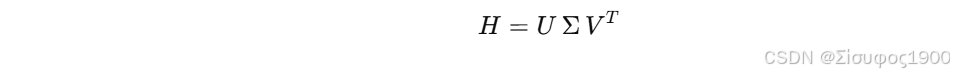
Step 4：旋转矩阵

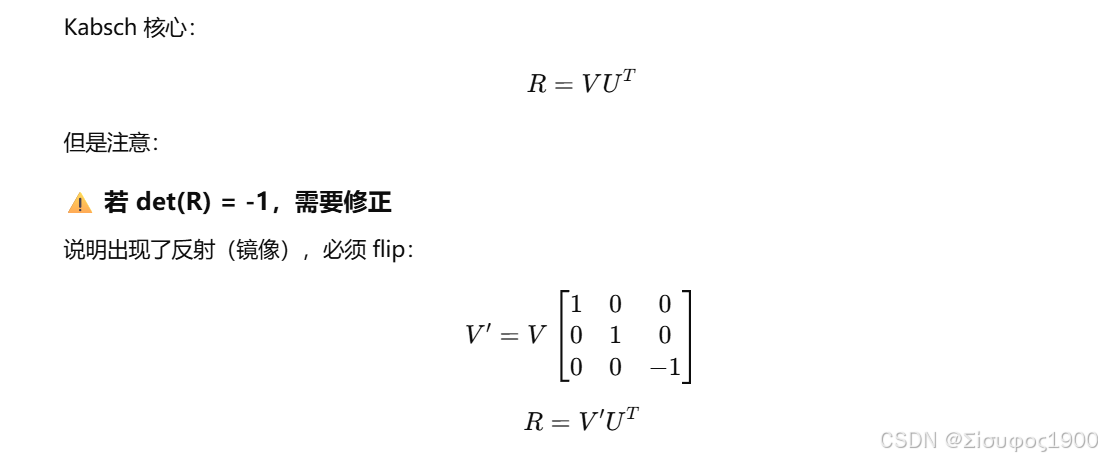
Step 5：平移

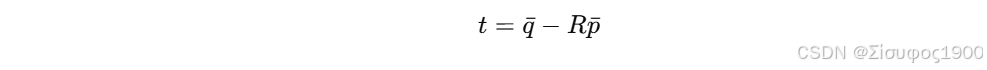
这就是 ICP 中的 R、t 更新

5、几何解释

⭐ 1. 去中心化 → 去掉平移，只剩形状

让两个点云绕中心对齐。

⭐ 2. H = Σ pᵢ qᵢᵀ → 统计它们方向上的相关性

反映两个点云的"共同指向"。

⭐ 3. SVD → 找到最接近正交矩阵的线性映射

SVD 会把矩阵分解成旋转 × 缩放 × 旋转。

⭐ 4. V Uᵀ → 去掉缩放，只留下旋转

所以它得到的是最优旋转。

这就是 最小二乘意义下点云最优刚体旋转。

6、Kabsch 算法 MATLAB 完整实现

cpp 复制代码

function [R, t] = kabsch(P, Q)
    % 输入：P, Q (N×3), 按对应点排列
    % 输出：R (3×3), t (3×1)

    % 1. 去中心化
    p_bar = mean(P, 1);
    q_bar = mean(Q, 1);
    P0 = P - p_bar;
    Q0 = Q - q_bar;

    % 2. 协方差矩阵
    H = P0' * Q0;

    % 3. SVD
    [U, ~, V] = svd(H);

    % 4. 旋转
    R = V * U';
    if det(R) < 0
        disp('Reflection detected. Fixing...');
        V(:,3) = -V(:,3);
        R = V * U';
    end

    % 5. 平移
    t = q_bar' - R * p_bar';
end

cpp 复制代码

      两组点云
   P ● ● ● ● ●
   Q ○ ○ ○ ○ ○

Step1 去中心化
Step2 构造 H
Step3 SVD → U, Σ, V
Step4 R = V Uᵀ
Step5 t = q̄ - R p̄

完成最优刚体对齐

7、在 ICP 中的作用

ICP 的一轮迭代流程：

建立最近点对应
使用 Kabsch 求解 R, t
更新点云
收敛