Leetcode热题中的：回溯专题

前言

只用java。

递归的通用套路

1.分析画树形结构，思考问题过程

2.递归的返回值的含义：子问题向父问题汇报结果，比如二叉树的左子树和右子树

3.递归的参数的含义：解决问题必要的参数

4.递归的退出条件

5.递归的回溯操作

17.电话号码的字母组合

方法1：递归回溯
难点1：对于组合问题能不能想到递归和回溯
分析1：任何这种递归回溯问题都可以化成树形结构。从abc开始，依次取不同字母，然后再从def开始，依次取不同字母，而调用完毕后需要回溯，因为存在其他组合，这就是思路。

用一下代码随想录的板书，推荐大家去看，很有用

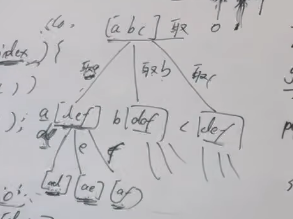
难点2：为什么Java的字符串拼接这么慢
分析2：因为Java的字符串是不可变的，底层进行字符串拼接的时候，会重新分配一个内存空间，将两个字符串进行拼接，这个过程的时间开销和空间开销就来了。所以我们只用字符串缓冲区进行缓冲，字符串缓冲区就不需要重新分配一块空间，所以我们使用字符串缓冲builder来进行回溯和递归。

java 复制代码

class Solution {
    // 留一个问题 Java的字符串拼接为什么慢
    public List<String> res = new ArrayList<>();
    public List<String> letterCombinations(String digits) {
        int n = digits.length();
        if(n == 0) {
            return res;
        }
        StringBuilder builder = new StringBuilder();
        findStr(digits, 0, builder);
        return res;
    }
    private String getStr(Character numChar) {
        String[] phone = new String[]{"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
        return phone[numChar - '0'];
    }

    // digits是传入的字符串 index是指向填充字符的位置 currStr是现在的字母组合
    private void findStr(String digits, int index, StringBuilder builder) {
        // 如果索引到n说明填充好一个组合了
        if(index == digits.length()) {
            res.add(builder.toString());
            return;
        }
        String digitStr = getStr(digits.charAt(index));
        for(int i = 0; i < digitStr.length(); i++) {
            builder.append(digitStr.charAt(i));
            findStr(digits, index + 1, builder);
            // 回溯
            builder.deleteCharAt(builder.length() - 1);
        }
    }
}

方法2：队列，看看就好。

java 复制代码

class Solution {
    public List<String> letterCombinations(String digits) {
        // 1.获得哈希
        Map<Character, String> hash = getHash();
        // 2.遍历digits
        int n = digits.length();
        // 3.准备一个双端队列deque作为队列
        Deque<String> deque = new ArrayDeque<>();
        deque.addLast("");
        for(int i = 0; i < n; i++) {
            String currStr = hash.get(digits.charAt(i));
            int size = deque.size();
            // 将队列中的元素全部进行拼接
            for(int j = 0; j < size; j++) {
                String head = deque.removeFirst();
                // 将新数字的每个字母和队列中的各个元素进行拼接
                for(char each : currStr.toCharArray()) {
                    deque.addLast(head + each);
                }
            }
        }
        return new ArrayList(deque);
    }

    // 准备哈希
    private Map<Character, String> getHash() {
        Map<Character, String> hash = new HashMap<>();
        hash.put('2', "abc");
        hash.put('3', "def");
        hash.put('4', "ghi");
        hash.put('5', "jkl");
        hash.put('6', "mno");
        hash.put('7', "pqrs");
        hash.put('8', "tuv");
        hash.put('9', "wxyz");
        return hash;
    }
}

反思：我没有想到递归，要多分析题目，特别是这种组合问题，它是需要回溯的，通过画树型结构，就明白这种组合问题是需要回溯和递归的，我下次遇到组合问题，应该优先考虑一下回溯算法。我没有想到字符串 - '0'转化成数字的快速操作，我下次遇到字符转化为数字，就应该想到减去字符'0'的这种操作。

22.括号生成

分析1：首先求括号的组合，括号是有效的，这说明左括号要先放，可以想到第一种解法，利用栈的特性，将左括号和右括号的所有组合列举出来再通过判断，注意是左括号入栈右括号出栈，只有一种括号可以不用模拟出栈，直接用数学简化版
难点2：回溯法是怎样剪枝的？
分析2：在任何时候右括号的数量都 <= 左括号，为什么？因为我们的括号必须是合法的，所以第一个必须是左括号，无论你第二个放什么括号，左括号都大于等于右括号的数量，所以说在放完左括号以后，我们只需要 y < x 就可以进行放右括号的操作了，否则会多出很多不合理的组合

解法1：回溯法

java 复制代码

class Solution {
    public List<String> res = new ArrayList<>();

    public List<String> generateParenthesis(int n) {
        // 组合 + 有效
        StringBuilder builder = new StringBuilder();
        findRes(n, 0, builder, 0, 0);
        return res;
    }

    // n是括号对数 index是填充的下标位置 builder是当前的结果 x是左括号的个数 y是右括号的个数
    private void findRes(int n, int index, StringBuilder builder, int x, int y) {
        if (index == 2 * n) {
            res.add(builder.toString());
            return;
        }
        // 先填左括号
        if (x < n) {
            builder.append("(");
            findRes(n, index + 1, builder, x + 1, y);
            // 回溯
            builder.deleteCharAt(builder.length() - 1);
        }
        // 再填右括号
        if (y < x) {
            builder.append(")");
            findRes(n, index + 1, builder, x, y + 1);
            // 回溯
            builder.deleteCharAt(builder.length() - 1);
        }

    }
}

解法2：利用栈

java 复制代码

class Solution {
    public List<String> res = new ArrayList<>();

    public List<String> generateParenthesis(int n) {
        // 组合 + 有效
        StringBuilder builder = new StringBuilder();
        findRes(n, 0, builder, 0, 0);
        return res;
    }

    // n是括号对数 index是填充的下标位置 builder是当前的结果 x是左括号的个数 y是右括号的个数
    private void findRes(int n, int index, StringBuilder builder, int x, int y) {
        if (index == 2 * n) {
            // 判断是否有效
            if (isCorrect(builder.toString())) {
                res.add(builder.toString());
            }
            return;
        }
        if (x < n) {
            builder.append("(");
            findRes(n, index + 1, builder, x + 1, y);
            // 回溯
            builder.deleteCharAt(builder.length() - 1);
        }
        if (y < n) {
            builder.append(")");
            findRes(n, index + 1, builder, x, y + 1);
            // 回溯
            builder.deleteCharAt(builder.length() - 1);
        }

    }

    // 判断括号是否有效
    private boolean isCorrect(String str) {
      int banance = 0;
      for(int i = 0; i < str.length(); i++) {
        if(str.charAt(i) == '(') {
            banance++;
        }
        if(str.charAt(i) == ')') {
            banance--;
        }
        if(banance < 0) {
            return false;
        }
      }
      return true;
    }
}

反思：我没有想到它天然的满足的条件就是左括号的数量永远都大于等于右括号，应该多观察

39.组合总和

难点1：res.add(new ArrayList<>(curr));中curr是全程更新的记录结果的list，我们需要让res保存所有当时curr满足sum == target的状态，那么curr需要拷贝一份，而不是直接add，如果直接add就会指向同一地址，res里面的结果也会跟着更新
难点2：利用循环来不断寻找满足target的值，包括了自己，所以进行下一步递归的时候，index还是i，也就是从自己开始，不满足就会回溯，进行curr去掉最新加入的元素然后进一步寻找

java 复制代码

class Solution {
    public List<List<Integer>> res = new ArrayList<>();
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<Integer> curr = new ArrayList<>();
        findCombine(candidates, 0, target, curr, 0);
        return res;
    }
    private void findCombine(int[] candidates, int sum, int target, List<Integer> curr, int index) {
        if(sum == target) {
            // 创建新引用 否则会一直指向同一地址 最后回溯的结果还是空
            // new ArrayList<>(另一个List)是表示拷贝这个List的意思
            res.add(new ArrayList<>(curr));
            return;
        }
        if(sum > target) {
            return;
        }
        for(int i = index; i < candidates.length; i++) {
            curr.add(candidates[i]);
            findCombine(candidates, sum + candidates[i], target, curr, i);
            curr.remove(curr.size() - 1);
        }
    }
}

46.全排列

借用一下代码随想录的递归树

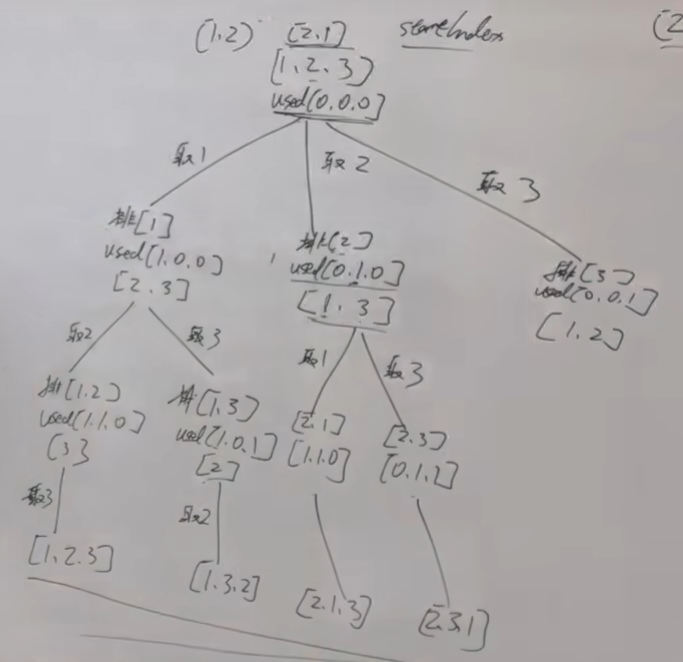
分析：首先我们之前做过组合，而组合是可以重复取的，比如(1,2)和(2,1)都是一个结果，而排列不同，排列有顺序的，首先我们需要填数，所以要用for循环，为了防止我们取重复的数，我们需要一个标记数组来标志这个数有没有被填过，因为题目中说了是不含重复的元素，第二，我们需要回溯，取消标志和去除current中存入的数据，第三，for循环从0开始而不是index开始，是因为排列是有顺序的，每次都需要从0开始寻找，而组合从index开始，因为1 2 3和 2 3 1是一样的排列，所以不用回头，所以没有顺序问题

java 复制代码

class Solution {
    // 1.存放输出
    private List<List<Integer>> res = new ArrayList<>();

    public List<List<Integer>> permute(int[] nums) {
        // 2.标记数组 标记我们已经填入的数
        boolean[] used = new boolean[nums.length];
        pushBack(nums, new ArrayList<>(), used);
        return res;
    }

    private void pushBack(int[] nums, List<Integer> current, boolean[] used) {
        if (current.size() == nums.length) {
            // 注意1: current必须拷贝 而不是直接填入 不然都指向同一个引用 没有记录最终答案
            res.add(new ArrayList(current));
            return;
        }
        // 3.填入数字
        for(int i = 0; i < nums.length; i++) {
            // 如果这个数已经被填过了就跳过
            if(used[i]) {
                continue;
            }
            // 如果没有被填过就填入current
            current.add(nums[i]);
            used[i] = true;
            // 4.进入下一次填数
            pushBack(nums, current, used);
            // 5.进入下一次填数需要回溯 因为有不同的排列
            used[i] = false;
            current.remove(current.size() - 1);
        }
    }
}

反思：我没有想到标记数组的作用，标记数组可以方式无限递归，并且可以筛选递归的元素

78.子集

分析：首先，子集是一个集合，它是组合问题，所以从index开始，第二，它的结果不是在叶子节点，而是在每个节点，只要能够递归，说明就有记录，第三，空集和本身的问题，可以传入时就记录current，把所有能递归的结果保存下来就可以了

java 复制代码

class Solution {
    // 1.记录答案
    private List<List<Integer>> res = new ArrayList<>();
    
    public List<List<Integer>> subsets(int[] nums) {
            // 递归
            pushBack(nums, 0, new ArrayList<>());
            return res;
    }
    private void pushBack(int[] nums, int index, List<Integer> current) {
        // 到一个节点就满足条件添加记录
        res.add(new ArrayList<>(current));
        for(int i = index; i < nums.length; i++) {
            current.add(nums[i]);
            pushBack(nums, i + 1, current);
            current.remove(current.size() - 1);
        }
    }
}

79.单词搜索

分析：显然这是搜索问题，只能上下左右移动，所以依次需要上下左右递归，第二，搜索路径问题需要标记走过的位置，避免进入无限递归，所以需要一个visited，第三，匹配字符串，只需要比较当前位置和字符串的当前位置进行比较就可以了，count记录现在匹配到字符串的哪一个地方了，当count = 字符串的长度的时候说明匹配成功了，第四，从各个起点开始，所以需要遍历各个起点

java 复制代码

class Solution {
    
    private boolean exist = false;

    public boolean exist(char[][] board, String word) {
        int m = board.length;
        int n = board[0].length;
        boolean[][] visited = new boolean[m][n];
        for(int i = 0; i < board.length; i++) {
            for(int j = 0; j < board[0].length; j++) {
                findBack(board, i, j, word, 0, visited);
            }
        }
        return exist;
    }
    private void findBack(char[][] board, int x, int y, String word, int count, boolean[][] visited) {
        // 找到更新并返回
        if(count == word.length()) {
            exist = true;
            return;
        }
        // 越界直接返回
        if(x < 0 || y < 0 || x >= board.length || y >= board[0].length) {
            return;
        }
        // 已访问直接返回
        if(visited[x][y] == true) {
            return;
        }
        // 不匹配直接返回
        if(word.charAt(count) != board[x][y]) {
            return;
        }
        count++;
        visited[x][y] = true;
        // 上
        findBack(board, x - 1, y, word, count, visited);
        // 下
        findBack(board, x + 1, y, word, count, visited);
        // 左
        findBack(board, x, y - 1, word, count, visited);
        // 右
        findBack(board, x, y + 1, word, count, visited);
        // 回溯
        visited[x][y] = false;
    }
}

反思：我没有想到标记数组的用法，我没有用count来这样巧妙地匹配，而是用StringBuilder来比较，其实也可以，只不过维护成本更高

131.分割回文串

分析：我觉得这道题没什么难的，其实就是把字符串分割为全是回文串的子串就可以了，以index为起点，向右边遍历，寻找index到i组成的回文串，如果是，那么index从i + 1开始，因为之前的index到i已经是回文串了，下一次就从i + 1开始分割，因为我们要确保子串全部都是回文串，就行了

java 复制代码

class Solution {
    
    List<List<String>> res = new ArrayList<>();
    List<String> path = new ArrayList<>();
    
    public List<List<String>> partition(String s) {
        pushBask(0, s);
        return res;
    }

    private void pushBask(int index, String s) {
        if(index == s.length()) {
            res.add(new ArrayList<>(path));
            return;
        }
        for(int i = index; i < s.length(); i++) {
            if(isPalindrome(s, index, i)) {
                path.add(s.substring(index, i + 1));
                // 从i + 1处开始递归 因为我们要把所有子串都递归成回文的 
                // 此时index到i已经是回文了 所以从i + 1开始递归
                pushBask(i + 1, s);
                // 回溯
                path.remove(path.size() - 1);
            }
            // 如果不是回文字符串就继续向前搜索
        }
    }

    /**
        双指针判断回文字符串
     */
    private boolean isPalindrome(String s, int left, int right) {
        while(left < right) {
            if(s.charAt(left) != s.charAt(right)) {
                return false;
            }
            left++;
            right--;
        }
        return true;
    } 
}

51.N皇后

分析：放置皇后，我们放置皇后的时候是从棋盘上面开始放，那么我们一行只能放一个，且一列只能放一个，对角线不能放，对角线能不能放我们就判断左上和右上就行了，因为我们是从上往下放皇后的，一行放一个，我们就用x来表示就行了，放了一个就立马跳到下一行就行了，刷了这么久来感觉了

java 复制代码

class Solution {
    private List<List<String>> res = new ArrayList<>();

    public List<List<String>> solveNQueens(int n) {
        int[][] chess = new int[n][n];
        backtrack(chess, 0, n); // 从第0行开始放
        return res;
    }

    private void backtrack(int[][] chess, int x, int n) {
        // 放完n行，收集一个解
        if (x == n) {
            res.add(buildBoard(chess, n));
            return;
        }

        // 在当前行，尝试每一列
        for (int y = 0; y < n; y++) {
            if (isTrouble(chess, x, y, n)) {
                continue;
            }
            chess[x][y] = 1;          // 放皇后
            backtrack(chess, x + 1, n);  // 递归下一行
            chess[x][y] = 0;          // 回溯
        }
    }

    // 判断 (x,y) 是否与已放皇后冲突 只需要看上方 因为我们从上摆到下
    private boolean isTrouble(int[][] chess, int x, int y, int n) {
        // 没有检测行是因为我们本身一行就只有一个
        // 列：上方是否有皇后
        for (int i = 0; i < x; i++) {
            if (chess[i][y] == 1) {
                return true;
            }
        }

        // 左上
        for (int i = x - 1, j = y - 1; i >= 0 && j >= 0; i--, j--) {
            if (chess[i][j] == 1) {
                return true;
            }
        }

        // 右上
        for (int i = x - 1, j = y + 1; i >= 0 && j < n; i--, j++) {
            if (chess[i][j] == 1) {
                return true;
            }
        }

        return false;
    }

    // 把棋盘转成题目要求的 List<String>
    private List<String> buildBoard(int[][] chess, int n) {
        List<String> board = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            StringBuilder builder = new StringBuilder();
            for (int j = 0; j < n; j++) {
                builder.append(chess[i][j] == 1 ? 'Q' : '.');
            }
            board.add(builder.toString());
        }
        return board;
    }
}