我先根据图片把 Jacobi 线性迭代的"从 Ax=b 到迭代公式"的推导走一遍，再解释它为什么会收敛/何时会发散，并给一个小例子把公式落到实处。
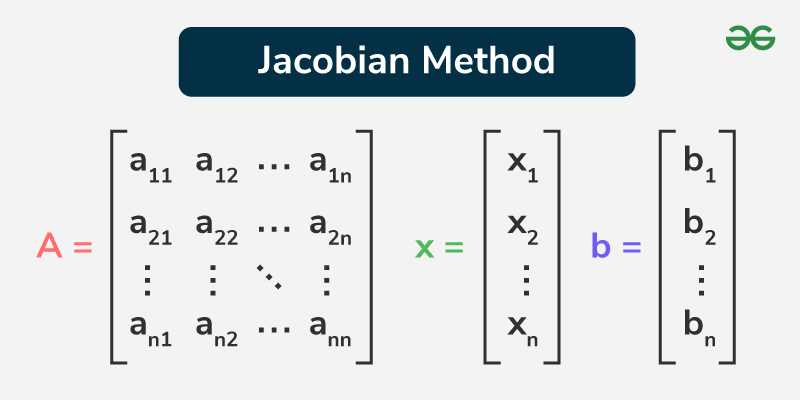
这张图在讲 Jacobi（雅可比）迭代法：要解线性方程组
它属于"线性迭代（stationary linear iteration）"的一类：把求解 Ax=b 变成一个固定点迭代
其中 B,c 由 A,b 构造出来。
1) 线性迭代的通用公式：矩阵分裂（splitting）
把 A 拆成
A=M−N
其中 M 选得"容易求解"（比如对角矩阵或三角矩阵）。原方程
移项得
(1.1) 先做纯代数变形（没有 k）
前提：M 可逆 （否则 不存在）。
对等式两边左乘 ：
左边 ，所以
把它写成"固定点"形式：
到这里为止，还是同一个方程的等价写法，并没有"迭代"。
(1.2) 再把固定点方程变成迭代（引入 k）
固定点方程 x=F(x) 的经典求解方式是：
从一个初值 出发，不断做
把上面的 F(x) 代进去：
所以
这就是迭代公式。
(1.3) 直觉：为什么可以这么做？
-
原式 Mx=Nx+b 的意思是：真解
同时满足
-
迭代的意思是：我先随便猜一个
-
如果这个映射 F 有"收缩"性质（本质上对应
(1.4) 一句话总结
-
Mx=Nx+b 左乘
-
再用固定点迭代用旧的
这就是"线性迭代及其公式"的核心：选一个好解的 M，把难点挪到右边，用上一步的 去近似。
2) Jacobi 迭代：用对角线当 M
把 A 分成对角 + 非对角：
A=D+(L+U)
-
D：对角部分（只保留
-
L：严格下三角
-
U：严格上三角
Jacobi 的选择是：
代入通用公式：
也常写成
分量形式（最直观、也最像"按行更新"）
从第 i 行方程
把 单独拎出来：
于是 Jacobi 的更新是
注意：右边 全部用旧迭代 k 的值（这是 Jacobi 的特征）。
3) 为什么叫"迭代"？误差传播公式一眼看懂
设真解为 ，误差
。由
相减得
再迭代：
所以收敛（误差趋于 0）的关键就是：会不会趋于 0。
4) 收敛判据：谱半径（和 ρ(A)强相关）
线性迭代 收敛到唯一固定点的经典条件是：
ρ(B)<1
其中 （谱半径）。直觉上：B 的"放大因子"最大也得小于 1，误差才能越乘越小。
对 Jacobi 来说就是
常见的"足够条件"（好用但不是必要条件）
如果 A 严格对角占优：
则 Jacobi 一定收敛（并且通常收敛挺稳）。
5) 一个 2×2 小例子，把公式落地
解
Jacobi 分量更新：
取初值 ：
-
k=0→1：
-
k=1→2：
-
k=2→3：
会在真解附近来回"拉近"，逐步收敛。
6) 线性迭代法家族（ Jacobi 只是其中一个）
同样从 A=D+L+U 出发：
-
Jacobi：用旧值更新（并行友好）
-
Gauss--Seidel：一更新就立刻用新值（通常更快）
-
SOR（加松弛 ω\omegaω）：在 GS 上再"加速/减速"
它们本质都符合： 以及收敛判据 ρ(B)<1。
那我就用一个 3×3 的具体数值例子把 Jacobi 线性迭代的"矩阵分裂 → 迭代矩阵 B → 谱半径 ρ(B) → 实际迭代过程"完整走一遍。
例子：解 Ax=b
先看一个常用的收敛"足够条件"------严格对角占优：
-
第1行：∣4∣>∣1∣+∣1∣=2
-
第2行：∣7∣>∣2∣+∣1∣=3
-
第3行：∣12∣>∣1∣+∣−3∣=4
所以 Jacobi 通常会收敛（这不是必要条件，但很实用）。
1) 矩阵分裂：A=D+L+U
2) Jacobi 的迭代公式（矩阵形式）
Jacobi 取 M=D，于是
写成标准"线性迭代"：
其中
把它们算出来：
3) 收敛为什么看谱半径
误差 满足
所以只要 反复乘会"越来越小"，误差就会消失。这个"会不会越来越小"的核心指标就是：
本例中 的特征值约为
因此
结论：收敛（而且因为谱半径不大，收敛会比较快）。
4) 真正迭代几步看看（从 开始）
Jacobi 分量公式就是（对应图片里的"按行解出每个 "）：
迭代结果（四舍五入到 6 位）：
| k | |||
|---|---|---|---|
| 0 | 0.000000 | 0.000000 | 0.000000 |
| 1 | 1.750000 | -0.142857 | 0.833333 |
| 2 | 1.577381 | -0.761905 | 0.651786 |
| 3 | 1.777530 | -0.686650 | 0.511409 |
| 4 | 1.793810 | -0.723781 | 0.513543 |
| 5 | 1.802559 | -0.728738 | 0.502904 |
| 6 | 1.806458 | -0.729718 | 0.500936 |
而这个方程组的真解是：
你会看到数值很快贴近。
在上篇文章《什么是矩阵的谱半径》中，出现了一个公式：
它是线性迭代（或线性动力系统）中一个非常重要且基础的特例公式 。它与我们之前讨论的通用形式紧密相关，其核心在于描述了一个齐次（没有常数项）的线性迭代过程。
1. 公式解析
-
变量含义：
- A 是一个方阵 ，被称为状态转移矩阵 或系统矩阵。它完全决定了系统如何从当前状态演化到下一步状态。
- x0 是初始状态向量。
-
公式解释：
- 第一个等式
- 箭头推导出的第二个等式
- 第一个等式
2. 与通用定义的关系
您之前看到的通用线性迭代公式为 。
- 图片中的公式是上述通用形式在 c=0（即没有外加常数项）时的特例。此时，迭代矩阵 B 就是图中的矩阵 A。
- 这种齐次形式描述的是一种"自生"的系统演化，每一步的变化完全由当前状态和固定的变换规则 A 决定，没有外部输入或偏移。
总结来说，此公式是齐次线性动力系统的核心迭代关系。 它通过 这一简洁形式，将系统状态直接与初始状态和矩阵的幂联系起来。而利用特征分解，我们可以深刻洞察该系统在不同方向上是如何被放大、衰减或维持的，这是分析系统稳定性、收敛性和长期行为的最强大工具之一。