22_不仅压缩还能生成?自编码器与流形学习
本章目标 :从判别式模型转向生成式模型 (Generative Models)。理解自编码器 (Autoencoder) 如何通过"自己骗自己"来学习数据的压缩表示,并初步接触"流形学习"的概念。
目录
- 无监督学习:没有标签怎么学?
- [Autoencoder 架构:瓶颈的艺术](#Autoencoder 架构:瓶颈的艺术)
- 信息瓶颈理论 (Information Bottleneck)
- [去噪自编码器 (Denoising AE):BERT 的前身](#去噪自编码器 (Denoising AE):BERT 的前身)
- [实战:PyTorch 实现图片降噪](#实战:PyTorch 实现图片降噪)
1. 无监督学习:没有标签怎么学?
之前我们学的都是 有监督学习 (Supervised) :输入是一张猫的图,标签是 "Cat"。
但在现实世界中,大部分数据是没有标签的。
自编码器 (Autoencoder) 的核心思想是:输入 X,标签也是 X 。
我们要训练一个网络,让它输出的东西尽可能和输入一样。
Target = Input \text{Target} = \text{Input} Target=Input
这听起来像是在做无用功(恒等映射 f ( x ) = x f(x)=x f(x)=x)?如果我们直接复制粘贴,确实没用。
关键在于:我们要给网络制造困难。
2. Autoencoder 架构:瓶颈的艺术
为了避免网络直接复制粘贴,我们在中间加了一个瓶颈 (Bottleneck)。
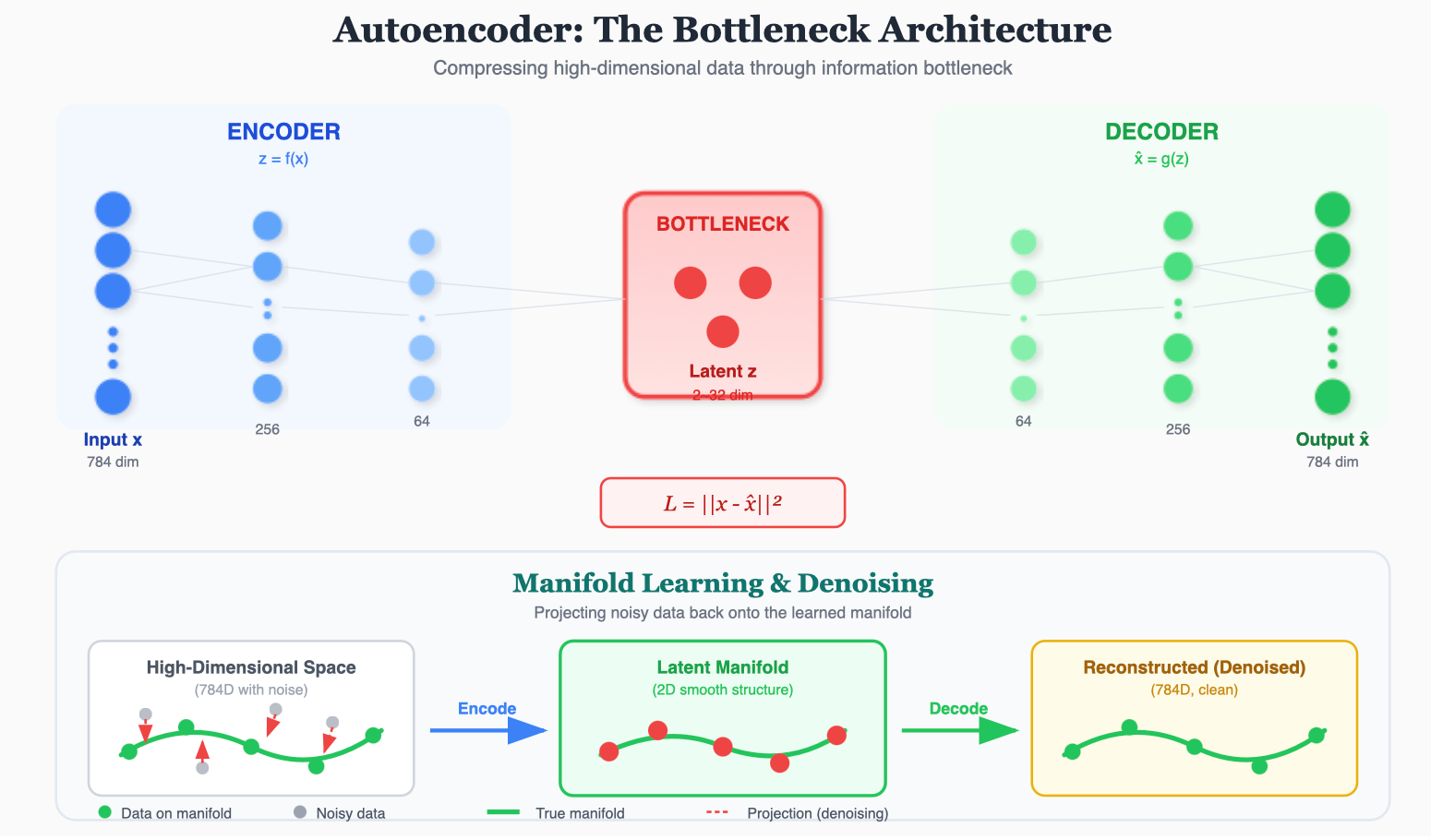
- Encoder (编码器) : z = f ( x ) z = f(x) z=f(x)。
- 将 784 维的图像压缩成极低维的 Latent Vector z z z(比如 2 维)。
- Decoder (解码器) : x ^ = g ( z ) \hat{x} = g(z) x^=g(z)。
- 试图从这可怜的 2 维信息中,还原出 784 维的原始图像。
- Loss : L = ∣ ∣ x − x ^ ∣ ∣ 2 L = ||x - \hat{x}||^2 L=∣∣x−x^∣∣2 (Reconstruction Loss).
3. 信息瓶颈理论 (Information Bottleneck)
因为 z z z 的容量远小于 x x x,Encoder 被迫学会只保留最重要的信息 (如数字的形状、笔画),并丢弃噪声(如背景杂点)。
这本质上是在做 流形学习 (Manifold Learning)。
- 假设 :高维数据(如图片)虽然看似维度很高(784),但其实它们分布在一个低维流形(如 2D 或 10D)上。
- Autoencoder 的目标:找到这个低维流形的坐标系。
这与 PCA(主成分分析)非常相似,但 Autoencoder 是非线性的,能力由神经网络的深度决定。
4. 去噪自编码器 (Denoising AE):BERT 的前身
为了强迫网络学到更鲁棒的特征,我们可以故意给输入加噪声:
- 加噪 : x ~ = x + Noise \tilde{x} = x + \text{Noise} x~=x+Noise (或者随机把一些像素涂黑/Dropout)。
- 目标 : x x x (原始干净图)。
- 训练 :让网络从 x ~ \tilde{x} x~ 还原出 x x x。
为什么有效?
看上图下方的 "Manifold Learning" 部分。
- 真实数据分布在绿色的流形曲线上。
- 加了噪声的数据点(灰色)偏离了流形。
- DAE 必须学会把偏离的点投影 (Project) 回正确的流形上。这就是"去噪"的本质。
这一思想后来被 BERT 发扬光大(Masked Language Model 本质上就是离散数据的去噪自编码器)。
5. 实战:PyTorch 实现图片降噪
我们训练一个 DAE 来去除 MNIST 图片上的噪声。
python
import torch
import torch.nn as nn
class Autoencoder(nn.Module):
def __init__(self):
super(Autoencoder, self).__init__()
# Encoder: 784 -> 128 -> 64 -> 3
self.encoder = nn.Sequential(
nn.Linear(28*28, 128),
nn.ReLU(),
nn.Linear(128, 64),
nn.ReLU(),
nn.Linear(64, 3) # Latent dim = 3
)
# Decoder: 3 -> 64 -> 128 -> 784
self.decoder = nn.Sequential(
nn.Linear(3, 64),
nn.ReLU(),
nn.Linear(64, 128),
nn.ReLU(),
nn.Linear(128, 28*28),
nn.Sigmoid() # 像素值在 0-1 之间
)
def forward(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return decoded
# 训练逻辑伪代码
# model = Autoencoder()
# criterion = nn.MSELoss()
# optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)
# for data, _ in dataloader:
# img = data.view(data.size(0), -1)
# # 关键:手动加噪声
# noisy_img = img + 0.5 * torch.randn(img.shape)
# noisy_img = torch.clamp(noisy_img, 0., 1.)
#
# # 输入是 noisy_img,目标是 img
# output = model(noisy_img)
# loss = criterion(output, img)
# ...局限性 :普通 AE 学到的 Latent Space z z z 是不连续的。如果你在两个数字的 z z z 之间插值,解码出来的可能是一堆乱码,而不是两个数字的渐变。
为了能生成 新图片,我们需要 VAE (变分自编码器)。