【图论和高阶拓扑学】智算数据中心容灾、网络健壮、迟滞性

图论和高阶拓扑学

特征维度	图论 (描述成对关系)	高阶拓扑学 (描述高阶交互)
核心要素	节点、边	单形/细胞、洞、贝蒂数
关系抽象	二元连接（点对点）	群体交互（如三角形、四面体结构）
结构分析	连通性、路径、中心度	同调群、贝蒂数（量化"洞"的数量）
关键工具	邻接矩阵、最短路径算法	持续同调、边界算子
优势	直观、计算效率相对较高	捕捉复杂系统的高阶依赖关系

1.1 从连接到结构：高阶拓扑的核心工具

高阶拓扑学的核心在于使用一系列强大的工具来揭示数据的内在结构。

持续同调 ：这是拓扑数据分析（TDA）的主力方法。它通过逐渐改变尺度参数（如连接点的距离阈值），系统性地观察拓扑特征（如连通组件、环状结构）的"出生"与"死亡"。那些在多个尺度下持续存在的特征，很可能代表了数据中稳健的结构，而短暂的特征则可能是噪声。其结果常以条形码 或持久图直观展示，条形码的长度直接体现了拓扑特征的稳定性。
单纯复形与细胞复形 ：这些是图的高维推广。单纯复形 由点、边、三角形、四面体等"单形"构成，并遵循特定规则（例如，一个三角形存在，则其三条边也必须存在）。细胞复形则更为灵活，允许粘贴更一般的二维或多维细胞。它们为描述复杂的群体交互提供了自然的框架。
霍奇拉普拉斯算子：该算子是图拉普拉斯算子向高维的推广。它不仅刻画了节点之间的关系，还描述了高维单元（如边、三角形）之间的互动。分析其频谱特性，有助于理解复杂网络中的扩散过程和高维结构。

洞察复杂系统的高阶拓扑

高阶拓扑分析方法已在多个领域展现出独特价值。

脑网络分析 ：在研究人脑结构连接组时，科学家发现除了成对的神经纤维连接，大脑中存在由多个脑区形成的密集连接子图（团）以及被连接通路环绕的拓扑洞。这些洞可能对应于功能相对隔离的脑区，其存在和持续性（通过持续同调分析）与大脑的信息处理机制密切相关。例如，在阿尔茨海默症等疾病中，可以观察到这些拓扑特征的异常变化。
复杂系统建模：在社交网络中，单纯复形可以模拟"同辈压力"（三个或更多人的相互影响）；在化学反应中，一个三角形可以表示三种反应物之间的协同作用。这些超越成对交互的情形，是图论难以直接描述的。
图神经网络（GNN）的增强 ：传统的GNN表达能力受限于WL同构测试。通过将输入图"提升"到细胞复形，在包含高维单元的新结构上进行拓扑信息传递，可以使GNN能够感知三角形、环等子结构，从而显著提升其区分和表示复杂关系的能力。

当高阶拓扑遇见图神经网络

将高阶拓扑结构与图神经网络结合，是当前一个非常前沿的方向。

拓扑信息传递 ：在细胞复形上，信息传递可以发生在不同维度的单元之间。不仅是节点之间，信息还可以从节点传递到边，从三角形传递到其边界上的边等。这种分层、跨维度的信息流动，使得模型能够更精细地刻画局部结构。
表达力的突破 ：基于细胞复形的细胞Weisfeiler-Lehman测试，其区分不同图结构的能力严格强于标准WL测试。这意味着，搭载了拓扑结构的GNN能够解决更多图论无法区分的结构问题。
缓解过度平滑：普通GNN在层数过深时，节点特征会趋向一致，称为"过度平滑"。高维细胞在图中创造了"捷径"，使得信息能在更少的步骤内远距离传播，有助于缓解此问题。

挑战与未来方向

尽管前景广阔，高阶拓扑学也面临一些挑战。首先是计算复杂度 ，高维拓扑不变量的计算成本远高于图算法。其次，如何为特定领域问题选择合适的拓扑表示 （如超图、单纯复形、细胞复形）仍需探索。最后，将这些复杂的数学工具集成到现有机器学习管道中，并使其可解释，也是一个重要的研究方向。

未来的发展可能会更深入地融合代数拓扑、微分几何的工具，并探索"蜂窝滑轮"等更抽象的结构。同时，也将更注重在生物、化学、社会科学等领域的实际应用，解决图论无法应对的复杂建模问题。

1.2 同调群和贝蒂数

1.2.1 在地图搜索算法的作用

同调群和贝蒂数这些来自代数拓扑的概念，为地图搜索算法提供了全新的视角。它们不再仅仅关注点对点的最短路径，而是通过分析道路网络整体的"形状"和"连通性"，来优化搜索效率和处理复杂空间关系。

下面这个表格总结了它们在地图搜索中的核心作用。

拓扑概念	在地图搜索算法中的作用	直观理解与地图对应
同调群 (Homology Group)	识别路网中的环形结构（如环岛、封闭街区）和无法连通的区域（如被河流、围墙隔开的区域）。	分析路网的"空洞"与"圈"的整体结构。
贝蒂数 (Betti Number)	β₀ ：连通分量数（如孤立的岛屿）。β₁：独立环路的数量（如环岛、大型环路的个数）。	β₀ ：地图被分割成几大块不连通的部分。β₁：地图上有多少个绕不开的"圈"。

如何优化地图搜索

基于上述核心作用，同调群和贝蒂数可以从以下几个层面优化传统的图搜索算法（如Dijkstra或A*算法）：

预处理与路径可行性验证

在开始复杂的路径计算前，可以先计算地图的0维同调群（即计算β₀）。如果起点和终点位于不同的连通分量中（β₀ ≥ 2且分属不同分量），算法能立即判断出路径不存在，避免无谓的全局搜索。这对于处理包含大型障碍物（如山脉）或跨海地图尤其有效。
指导搜索空间剪枝

高β₁值意味着路网中存在大量环路。传统的搜索算法可能会在这些环路中"兜圈子"。利用同调信息，可以为算法添加约束，例如，避免重复穿过由同调环定义的区域边界，从而引导算法更直接地朝向目标方向搜索，减少探索的分支数量。
提升复杂环境下的鲁棒性

当GPS信号漂移或地图数据局部缺失时，仅靠几何距离的匹配算法容易出错。结合了拓扑关系的匹配算法，会优先考虑道路的连通性（同调关系），从而避免将车辆位置匹配到拓扑结构不连贯的道路上（例如，突然跳到河对岸没有桥连接的路上），提高了导航的稳定性和准确性。

前沿视角：持续同调

对于动态变化或大规模的地图，**持续同调（Persistent Homology）** 这一工具更为强大。它通过一个"尺度参数"来观察拓扑特征（连通分量、环）的"出生"与"死亡"。

原理：想象一下，围绕每个道路交叉口画一个逐渐变大的圆圈。随着圆圈半径增大，孤立的点会逐渐连接成片，小的环路会被覆盖，而那些持续存在时间最长的连通分量和环路，就代表了路网最稳定的拓扑结构。
应用：在路径规划中，那些在多个尺度下都存在的"持久"环路（如城市主干道环线），可以被识别为关键路径。算法可以优先利用这些主干道进行长距离导航，因为它们拓扑结构稳定，能有效提升路径的可靠性和效率。

总而言之，同调群和贝蒂数作用于地图搜索算法，是从全局拓扑结构的层面提供深层指导。它们将搜索问题从纯粹的"几何距离优化"部分地转向了"拓扑结构分析"，通过识别关键的连通分量和环形回路，为算法提供了预处理、剪枝和鲁棒性增强的强大工具。

1.3 从图到单纯复形：为何需要高阶视角？

1.3.1 利用单纯复形对数据中心网络中的多点故障传播进行建模

利用单纯复形对数据中心网络中的多点故障传播进行建模，确实是一个深刻且前沿的视角。它超越了传统图论对"点对点"连接的描述，能够精准捕捉"多个组件同时失效"这一高阶协同故障的本质。

传统上，数据中心网络被抽象为一张图，节点代表服务器、交换机等设备，边代表物理或逻辑连接。当某个节点故障时，模型会模拟其影响如何沿边传播到邻居节点。

然而，现实中的故障往往更为复杂。例如：

冗余失效 ：一个由三台服务器构成的冗余集群（A、B、C），设计上允许任意一台故障。但若A、B同时故障，则可能导致整个集群服务中断。这种"三节点组"的集体失效效应，用传统的边（两两关系）无法完整描述。
共享依赖：多个虚拟机（VM）运行在同一台物理主机上，或者共享同一个电源模块。物理主机或电源的故障，会同时影响其上的所有虚拟机。

这时，单纯复形 的概念就派上了用场。一个 k-单纯形 是由 (k+1) 个节点构成的完全连接图，它能够直接表示这 (k+1) 个节点之间存在的高阶相互作用。

1-单纯形：就是一条边，描述两个节点间的成对关系。
2-单纯形：是一个实心三角形，描述三个节点之间不可分割的协同关系（如上述的冗余集群）。
单纯复形：则由这些不同维度的单纯形组合而成，但要求任何单纯形的面（例如三角形的边）也必须包含在该复形中。

建模步骤与核心方法

基于单纯复形构建故障传播模型，核心是定义一个负载-容量的动态级联过程。其关键步骤可概括为下表：

步骤	核心任务	关键说明
1. 网络抽象	将数据中心网络表示为单纯复形	识别系统中的高阶交互关系，例如，将共享同一关键资源（如交换机、电源）的一组设备建模为一个高阶单纯形。
2. 定义负载与容量	为每个节点定义初始负载 Li(0)和容量 Ci	负载可正比于节点的"广义度"（考虑其所属的1-单纯形和2-单纯形数量）。容量通常设定为初始负载的一个冗余比例，即 Ci=(1+T)⋅Li(0)，其中 T>0是容量参数。
3. 触发与重分配	模拟初始故障节点失效后的负载重分配	失效节点的负载会按一定规则分配给与之关联的单纯形（而不仅仅是邻居节点）。例如，与失效节点同属一个2-单纯形的另外两个节点会接收到额外的负载。
4. 级联传播	动态检查并传播故障	每次负载重分配后，检查所有节点是否满足 Li(t)>Ci。新失效的节点会触发新一轮的负载重分配，形成级联效应，直到网络重新稳定。
5. 评估影响	计算稳定后的网络连通度等指标	通过模拟不同节点失效、调整容量参数T或单纯形结构，可以评估网络的鲁棒性，识别脆弱环节。

案例示意

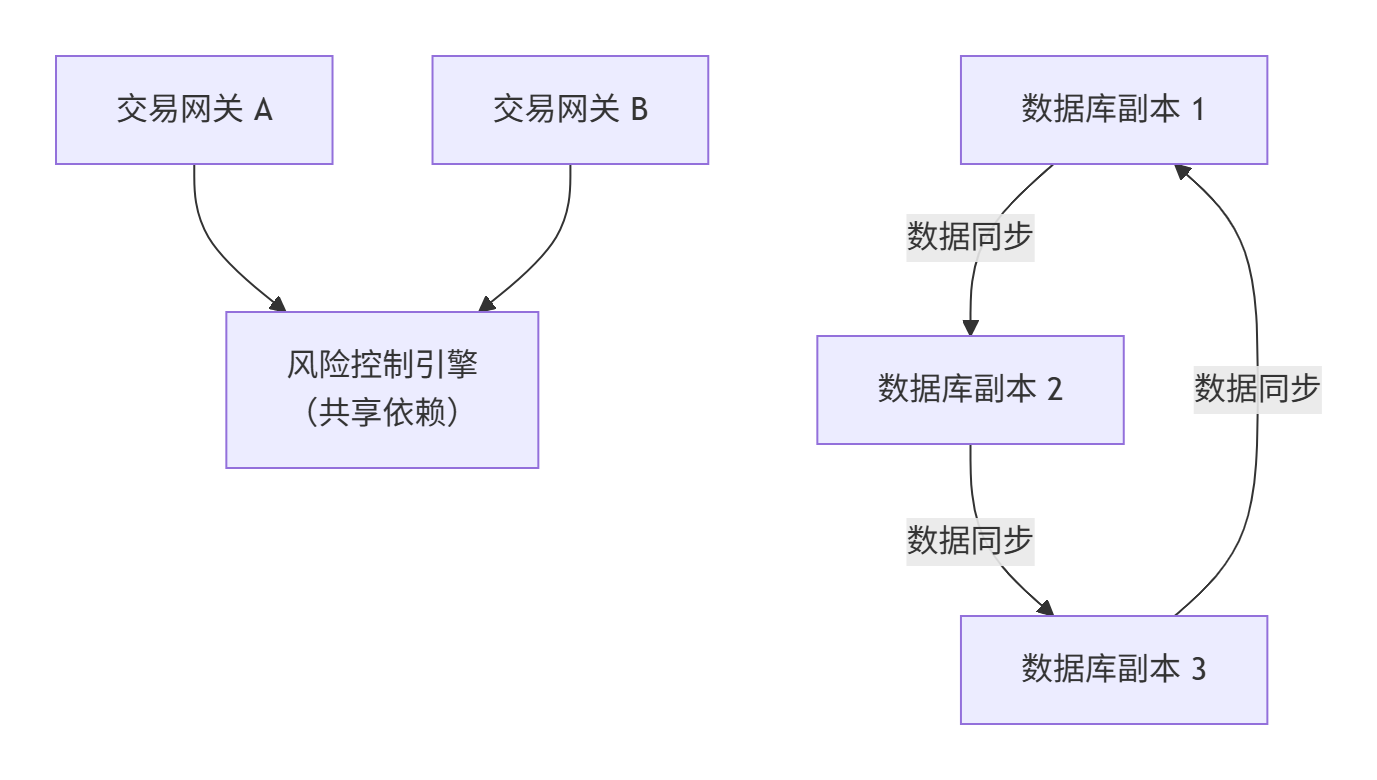
假设一个微型的金融交易系统包含6个节点，其逻辑关系如下图所示（请注意，下图是对拓扑关系的示意性表达）：

网络抽象：
- {交易网关A, 交易网关B, 风险控制引擎C}构成一个 2-单纯形（三角形）。因为两个网关高度依赖于同一个风控引擎，三者协同工作。
- {数据库副本1, 2, 3}构成另一个 2-单纯形。它们组成一个数据库集群，依赖数据同步（三边关系）。
- 这两个2-单纯形通过风控引擎C与数据库副本1之间的连接（1-单纯形）相关联。
故障模拟：
1. 假设 风险控制引擎C 因软件bug发生故障（初始故障）。
2. 根据模型，C的负载会重分配。由于C位于一个2-单纯形中，其负载会显著影响交易网关A和B。
3. A和B在接收到C的负载后，可能因过载而相继失效。此时，故障已从C传播至A和B。
4. 由于A/B的失效，以及C的失效，它们与数据库副本1的连接中断。数据库副本1可能因失去外部心跳或负载激增而失效。
5. 最终，故障通过高阶依赖（2-单纯形）和普通连接（1-单纯形）传播，可能导致整个数据库集群不可用，造成大规模服务中断。

总结与价值

通过单纯复形建模，我们能够更真实地反映数据中心网络因共享依赖、组协作 等产生的协同故障风险。这种模型的价值在于：

精准识别脆弱点：不仅能找到易故障的单个设备，还能识别出那些看似冗余但实际存在高阶依赖的"脆弱模块"。
优化资源布局：为网络规划提供理论依据，例如，避免创建过多包含关键资源的高阶单纯形，或有意将关键负载分散到拓扑上更独立的区域。
指导容灾策略：帮助设计更有效的故障隔离和切换方案，确保当高阶故障发生时，影响范围能被有效控制。

1.3.2 单纯复形在数据中心容灾领域的应用

单纯复形在数据中心容灾领域的应用，核心在于它提供了一种强大的数学工具，能够精准描述系统中组件之间复杂的高阶依赖关系，并在此基础上建模故障的传播过程，特别是负载-容量的动态级联失效。

拓扑概念	在数据中心容灾中的对应物	核心价值
0-单形 (点)	单个IT组件，如一台物理服务器、一个虚拟机、一个存储设备或一个网络交换机。	描述系统的基本构成单元。
1-单形 (边)	两个组件之间的双向依赖关系，例如一台应用服务器与其后端数据库服务器的连接。	描述传统的成对依赖，故障可能沿边传播。
2-单形 (实心三角形)	三个组件之间不可分割的协同关系，例如一个由三台服务器构成的冗余集群（A、B、C），任意两台故障会导致集群失效。	捕捉高阶依赖，这是图论难以描述的集体失效风险。
k-单形 (k≥2)	更复杂的群体交互，如多个微服务共同构成一个业务应用。	描述更广泛的系统性风险。
单纯复形	整个数据中心所有组件及其复杂依赖关系的统一拓扑模型。	为系统级的脆弱性分析和容灾规划提供整体框架。

负载-容量动态级联过程详解

单纯复形模型的价值，在于它能动态模拟一个初始故障如何因组件间的依赖关系，通过负载再分配引发连锁反应。其核心是一个负载-容量的动态级联过程，具体流程如下面的序列图所示：

复制代码

flowchart TD
    A[初始节点故障] --> B[负载重分配规则触发]
    B --> C[负载重分配给关联的单纯形]
    C --> D[检查关联节点新负载]
    D --> E{"新负载 > 节点容量?"}
    E -- 是 --> F[节点失效]
    F --> G[新一轮负载重分配]
    G --> C
    E -- 否 --> H[系统恢复稳定]

上述流程中的关键环节包括：

初始化：为每个节点（服务器等）定义两个关键参数：
- 初始负载 Li(0) : 节点i在正常状态下所承担的工作量。
- 容量 Ci : 节点i能够承受的最大负载，通常设定为 Ci=(1+α)⋅Li(0)，其中 α≥0是容量缓冲参数（Tolerance），代表节点的冗余能力。
触发与重分配（核心） ：当一个或多个节点因故障失效时（如上图所示），它们原本承担的负载并不会消失，而是会根据预设规则重新分配 给与之关联的其他节点。关键在于，负载不仅是分配给邻居节点（1-单形），更重要的是分配给包含该故障节点的所有高阶单纯形（如2-单形、3-单形）中的其他成员。例如，在一个2-单形（三角形）中，一个节点失效，其负载可能会由另外两个节点共同承担。
级联传播 ：每次负载重分配后，系统会检查所有节点。如果某个节点接收到的新负载 Li(t)超过了其容量 Ci，则该节点会因过载而失效。这些新失效的节点会触发新一轮的负载重分配，如流程图中的循环所示，从而可能引发链式反应，导致故障在整个网络中扩散。
稳定与评估 ：当再也没有节点因过载而失效时，级联过程停止。此时，可以评估此次事件造成的最终影响，例如计算最终失效的节点比例、网络连通性损失等，从而量化系统的鲁棒性。

应用价值与总结

通过基于单纯复形的建模，我们能够更真实地模拟和评估数据中心在面临故障时的行为。这种方法的价值在于：

识别系统性脆弱点 ：不仅能找到易故障的单点，还能识别出那些因高阶依赖而存在的潜在"脆弱模块"。
指导容灾资源规划：通过调整容量缓冲参数 α或改变网络拓扑（例如，有意识地减少高风险的高阶单纯形），可以在成本与可靠性之间找到最优平衡，为容灾策略提供定量依据。
优化故障隔离与切换策略：帮助设计更有效的应急预案，确保当高阶故障发生时，能快速隔离影响范围，实现业务平滑切换。

总而言之，单纯复形通过将数据中心抽象为包含高阶相互作用的拓扑结构，并定义负载-容量的动态级联规则，为我们提供了一种超越传统图论的、更强大的系统风险分析框架。这有助于从"形状"和"结构"的深层角度，构建更具韧性的数据中心容灾体系。

1.3.3 数据中心容灾体系与图论

数据中心容灾体系本质上是一个确保数据持久可用和业务连续性的复杂系统。

理论工具	在容灾体系中的核心角色	关键价值
集合与关系	定义容灾资源池（服务器、存储、网络设备等）及其亲和/反亲和规则。	形式化描述资源间的依赖与隔离约束，是自动化部署与调度的基础。
图与网络流	建模数据中心网络拓扑（如Spine-Leaf）、数据流与故障传播路径。	优化数据同步路径、分析故障影响范围、保障关键链路带宽。
编码理论	实现跨数据中心的高效数据容灾，如纠删码技术。	以远低于多副本的存储开销，获得更高的数据可靠性。
有限状态机	描述容灾流程（正常、切换、恢复等）中各实体的状态迁移。	使容灾流程标准化、可预测、可验证，避免因状态混乱导致操作失败。

1.3.3.1 集合与关系：资源管理的基石

容灾系统管理的所有实体，如物理服务器、虚拟机、存储卷、网络链路等，都可以抽象为元素。这些元素根据其属性（如地理位置、性能、功能）被划分到不同的集合中，例如"北京Region的所有服务器"或"用于数据库的SSD存储卷"。

更重要的是元素间的关系，这直接决定了容灾策略的有效性：

亲和性：要求某些应用对象必须部署在同一数据中心或可用区（AZ）内，以减少交互延迟。例如，一个Web服务器和其缓存服务可能存在亲和性关系。
反亲和性：要求关键应用的应用对象必须分散在不同的故障域。例如，一个应用的三副本应该部署在三个不同的可用区，甚至不同的地域（Region），以避免单一故障点导致服务完全中断。自动化容灾配置系统正是基于这些预定义的规则进行最优资源选择的。

1.3.3.2 图与网络流：拓扑与流量的蓝图

图论是分析数据中心网络结构的天然工具。

拓扑建模 ：现代数据中心普遍采用Spine-Leaf 的Clos架构，这本身就是一个二分图。服务器连接到Leaf交换机，Leaf交换机再全连接到Spine交换机。这种结构保证了任意两点间路径的等长短，避免了网络瓶颈。
流量优化 ：容灾过程中的数据同步可以建模为网络流问题。源数据中心是"源点"，目标数据中心是"汇点"，网络链路是带有带宽属性的"边"。运用最大流最小割定理，可以计算出数据中心间最大的数据同步能力，并规划最优的同步路径。
故障分析：通过分析图的连通性，可以快速模拟某个网络设备或链路故障后，哪些节点会变得不可达，从而评估故障的爆炸半径。

1.3.3.3 编码理论：数据可靠性的引擎

跨数据中心的容灾存储需要平衡可靠性、存储开销和网络带宽 。相较于简单的多副本技术（如3副本带来200%的存储开销），纠删码 技术展现出巨大优势。

其核心思想是：将一份数据分割成 k个数据块，通过编码计算生成 m个校验块，并将这 n=k+m个块分散存储在不同数据中心的不同节点上。只要任意 k个块存活，原始数据就可以完整恢复。例如，采用 (10,6) 纠删码，将数据分为10份并生成6份校验数据，然后分散到16个位置。即使同时损坏6份数据，数据依然可恢复，存储开销仅为60%，远低于多副本。

研究重点在于优化跨数据中心的修复流量。当某个数据块丢失时，高效的编码方法（如LDPC码、再生码）可以最小化重建数据所需从其他数据中心传输的数据量，从而大幅降低恢复时间。

1.3.3.4 有限状态机：流程控制的规范者

容灾切换与恢复不是一个单一动作，而是一个严格的状态转换过程。有限状态机 为此提供了精确的建模工具。

以主备数据中心切换为例，可以定义以下几个核心状态：

Normal（正常）：主中心运行，备中心同步数据。
Failure Detected（故障已检测）：监控系统发现主中心异常。
Switchover Initiated（切换已启动）：容灾管控端发出切换指令。在极端情况下，此指令甚至可通过带宽有限的卫星链路传输，并需有过滤机制确保只有关键指令通过。
Standby Promoted（备中心已升级）：备中心接管业务，变为新的主中心。
Recovery（恢复中）：原主中心修复后，重新同步数据并准备就绪。

FSM明确了每个状态的含义、触发状态迁移的事件（如"心跳丢失"、"手动切换命令"）、以及迁移时应执行的动作（如"挂起原主中心写入"）。这确保了整个流程的有序性和可预测性，避免了因状态混乱导致"脑裂"（即两个数据中心同时认为自己是主中心）等灾难性后果。

在真实的容灾系统中，这些理论并非孤立存在，而是紧密交织，共同构筑了体系的韧性。例如，一个容灾决策流程可能是：基于集合论 筛选出符合反亲和性规则的候选服务器集合；利用图论分析这些服务器间的网络延迟和带宽，并通过网络流 算法验证数据同步效率；最终，所有组件和流程的状态变迁都由有限状态机严格定义和控制。

1.3.3.5网络流算法与图论、单纯复形、几何学及复杂网络等数学理论在不同计算中心场景下的深层联系

网络流算法与图论、单纯复形、几何学及复杂网络等数学理论在不同计算中心场景下的深层联系。这些理论并非孤立的工具，而是共同构成了分析和优化现代大规模计算网络的基础。

应用场景	核心挑战	图论的角色	单纯复形的作用	几何学视角	复杂网络特性
数据中心容灾	跨中心数据同步的带宽优化、故障隔离与快速恢复（RTO/RPO）	将网络抽象为有向图（节点=设备，边=链路，容量=带宽），应用最大流/最小割算法（如Dinic算法）找瓶颈和最优数据路由。	建模多点协同故障（如共享同一电源的多台服务器同时宕机），描述超越成对连接的高阶依赖关系，从而更精准模拟故障传播范围。	将网络拓扑视为几何空间，利用网络坐标系统估算延迟，或将对偶图理论应用于平面化网络拓扑（如Fat-Tree），将最大流问题转化为最短路径问题，提升计算效率。	分析容灾网络的异构性（服务器、交换机、链路混合）与小世界特性（快速路由），设计健壮且高效的数据复制路径。
智算中心网络	满足AI训练（All-Reduce通信）、HPCC（计算/存储流水线）等密集型任务的高吞吐、低延迟需求。	不仅用图建模物理连接，更通过有向无环图（DAG）描述任务依赖关系，运用拓扑排序和关键路径法优化任务调度与资源分配。	对计算任务间的复杂协作模式（如多个Worker节点在参数服务器上的同步更新）进行建模，捕捉超越简单二元关系的群体交互行为。	在物理布局优化中，利用几何规划最小化服务器间通信距离；在逻辑上，将超立方体等拓扑嵌入网络，以优化大规模并行计算的全交换（All-to-All）通信。	智算中心网络是典型的异构（GPU/CPU/NIC）、高密度连接的复杂网络。其度分布、聚集系数等特性直接影响专用算法（如用于AI训练的流量调度算法）的设计。
智算中心组网需求	根据不同业务目标（如高性能计算、云服务、边缘协同）设计最优网络架构。	图划分算法（如Metis）用于将大规模计算任务映射到物理节点，最小化跨机柜流量。图谱理论可用于分析网络连通性和稳定性。	需求：需要能描述群体智能或集体负载的模型，以优化资源协同。如基于单纯复形的模型可帮助理解"多打一"（Incast）流量模式的内在结构。	需求：网络架构（如Dragonfly, Slim Fly）的设计本身依赖于离散几何（如使用有限几何构造低直径、高吞吐的网络图）。需求：通过微分几何工具分析网络流量的"曲率"，以识别潜在拥塞点。	需求：组网必须考虑网络的演化性（方便扩展）和韧性（抵抗攻击/故障的能力）。这需要利用复杂网络的鲁棒性分析方法进行设计评估。

核心关系解读

数据中心容灾方案中的协同

在数据中心容灾方案中，网络流算法 是实现资源优化调配的核心数学工具。例如，通过Dinic算法 或Edmonds-Karp算法 可以精确计算出在有限的跨数据中心带宽下，数据同步的最大可行流量 ，从而评估能否满足RPO（恢复点目标） 。最小割定理则能快速识别出网络中的脆弱环节，即那些一旦被切断就会导致数据同步中断的关键链路，为容灾链路的规划提供关键洞察。

然而，传统图论将依赖关系简化为点与点的连线，难以描述现实中"多个组件因共享同一底层资源而同时失效"的协同故障 场景。单纯复形 的引入，正好弥补了这一缺陷。它将一个由多个组件（如三台互为备份的服务器）构成的冗余单元 建模为一个高阶单纯形（如三角形），从而能够更精确地模拟和评估故障在系统内的传播范围和影响深度。此外，在评估跨数据中心延迟时，几何学 视角（如将网络节点映射到欧几里得空间）有助于优化网关选择和路径规划。而整个容灾网络作为一个复杂网络 ，其异构性 （混合设备）和小世界特性（快速路由）决定了容灾策略的设计必须考虑其整体拓扑特性。

智算中心网络的内在联系

智算中心网络是上述理论与方法集大成的场景。其核心任务是高效处理AI训练、高性能计算等产生的复杂数据流。图论不仅是描述网络物理拓扑的基础，其**有向无环图（DAG）** 更是对计算任务本身进行建模、调度和优化的标准工具。

同时，智算中心内计算任务间的高度协同特性，需要单纯复形 这类工具来建模群体交互行为 。例如，一个分布式机器学习任务中，多个参数服务器和工作节点之间形成的复杂同步模式，就是一个典型的高阶交互场景。几何学 的影响则更为直接：许多高性能网络拓扑（如Dragonfly）本身的设计就源于离散几何学 （如利用有限域上的线性代数构造出具有极大图规模的网络），旨在为大规模并行计算（如All-to-All通信）提供低延迟、高带宽的物理基础。自然，智算中心网络也是一个典型的复杂网络 ，其度分布 、聚集系数 等统计特性直接影响着专用流量调度算法的设计，而网络自身的演化性与韧性也是组网时必须考虑的核心因素。

总结与前瞻

总而言之，网络流算法提供了在约束条件下进行最优分配的计算方法 ；图论是描述网络组件关联的基础语言 ；单纯复形弥补了图论在描述群体高阶相互作用 方面的不足；几何学为网络物理拓扑和逻辑结构 提供了优化设计的深层原理；而复杂网络理论则从系统全局的统计规律和动力学行为角度，指导构建更健壮、更高效的计算中心基础设施。

这几者之间并非孤立，而是层层递进、相互补充的。对于一个智算中心的网络问题，我们既可以用图论描述其设备连接，用网络流算法 计算最大吞吐，也可以用单纯复形 分析其多节点通信模式的内在结构，还可以从几何学 角度优化其物理布局，并最终将其置于复杂网络的框架下评估其全局鲁棒性。

不同智算中心的组网架构，可以理解为在构建"超级计算机大脑"的"神经网络"时采用的不同布线蓝图。每种蓝图在连接效率、成本和控制信号（路由算法）的复杂性上有着根本性的差异。

架构特性	Spine-Leaf (CLOS)	Dragonfly / Dragonfly+	Slim Fly	DDC (轨道优化架构)
核心拓扑比喻	规则网格：像摩天大楼的承重结构，层级分明，路径固定且可预测。	航空枢纽：城市间直飞（全局链路）与市内交通（本地组）结合，追求最短跨组跳数。	高速公路网：基于数学（图论）精心设计的主干道，实现理论上任意两点间的最短路径。	多轨立交：为AI流量定制多条并行高速通道，大部分流量在"轨道"内直接交换。
网络直径	相对固定（例如3层架构直径为6跳）。	极低：任意两点间通信最多仅需 2跳（本地1跳 + 全局1跳）。	理论最优：基于数学（如Moore bound）优化，在给定节点和度下实现可能的最小直径。	可变：通过"轨道"化设计，目标是让大部分通信（>85%）在1跳内完成，优化All-to-All流量。
扩展性	优秀且线性：通过增加Spine或Leaf交换机数量即可平滑扩容，规则清晰。	极强：通过增加组内交换机数量或全局链路，可支持超10万卡的集群规模。	中等偏上：受限于其严格的数学构造，大规模扩展时可能不如Dragonfly灵活。	为AI定制：专为大规模AI训练（万卡级以上）设计，扩展性优秀。
路径多样性 (对偶图复杂度)	极高且均匀：任意两点间存在大量等价多路径，便于ECMP负载均衡。	混合型：组内路径丰富，但组间路径依赖有限的全局链路，易成瓶颈。	高度结构化：路径多样性由其数学定义（如凯莱图）决定，可能不如CLOS均匀。	聚焦局部：通过设计使高概率的通信模式（如AI训练中的All-Reduce）路径极短且确定。
关键优势	结构规则、易于管理和故障诊断、多路径负载均衡成熟可靠。	超低延迟（尤其对于跨组通信）、设备数量少、总体拥有成本低。	在给定的网络度（设备端口数）下，实现了理论上的最低直径和最高效率。	为AI流量量身定制，显著降低大规模训练的通信延迟和成本。
潜在挑战	规模极大时，交换机数量和布线成本较高；网络层数可能增加延迟。	全局链路拥塞风险；需要复杂的非最小路径路由算法来避免热点。	拓扑结构相对固定，硬件生态和支持度目前可能不如前两者成熟。	拓扑特异性强，与通用业务的兼容性、运维工具链需重新构建。

深入理解关键差异

以上表格中的特性，源于这些架构根本的设计哲学，这直接影响了它们的"复杂网络特性"和"对偶图"分析。

复杂网络特性的体现
- 小世界特性与网络直径 ：Slim Fly 和 Dragonfly 的核心目标就是打造一个"小世界网络"，即网络的平均直径非常小。这意味着信息从任何一个节点到另一个节点所需要经过的"中转站"（交换机）数量极少，这对于降低AI分布式训练中频繁的全局通信（All-Reduce）延迟至关重要。
- 度分布 ：在 Spine-Leaf 中，Leaf交换机的"度"（连接数）较小且固定，Spine交换机的"度"很大。这是一种异构的度分布。而 Slim Fly 的度分布可能更为均匀，因为其设计目标之一就是在固定度下最大化网络规模。
- 拥塞与鲁棒性 ：Dragonfly 的挑战在于其全局链路 可能成为瓶颈。当多个组同时需要相互通信时，这些有限的直连链路容易发生拥塞，需要高级的路由算法（如VALIANT ）将流量随机分散到其他组进行"绕行"（非最小路径路由）。而 Spine-Leaf 的鲁棒性来自于其丰富的等价多路径，单条链路或单台交换机的故障很容易被绕过。
对偶图视角的洞察

"对偶图"是将原网络中的交换机视为节点，将链路视为边，重新绘制的一张图。这个视角对于分析路由效率 和网络可分区性至关重要。
- 在 Spine-Leaf 的对偶图中，会呈现出一个标准的二分图，结构非常规则，这使得路由算法（如ECMP）可以简单高效地工作。
- Dragonfly 的对偶图会呈现出若干个全连接的完全子图（代表每个组内部），这些子图之间再通过少量的边（全局链路）连接。这个结构清晰地揭示了其脆弱性：那些连接子图的边是网络的关键。
- Slim Fly 的对偶图则可能对应着某种强正则图 或凯莱图，具有优异的代数性质，这保证了其优越的性能。

如何为智算中心选择合适的架构？

选择哪种架构，取决于你的核心目标：

追求极致性能与大规模扩展 ：当你的目标是构建万卡乃至十万卡级别的超大规模集群以训练千亿参数大模型时，Dragonfly+ （或其变种 Groupwise Dragonfly+ ）和专为AI优化的 DDC 架构是优先选择。它们能以更少的设备数量、更低的延迟实现超大规模互联，显著降低总拥有成本。
平衡通用性与可管理性 ：如果你的集群规模在数千卡以内，或者需要同时承载AI训练、HPC、云计算等多种混合工作负载，Spine-Leaf 是久经考验的稳妥选择。其规则的结构和成熟的运维工具链能大大降低管理复杂度。
探索前沿与理论最优 ：如果在特定规模下追求理论上的最低延迟和最高效率，并且愿意接受一定的技术风险，Slim Fly 这样的基于高级图论设计的架构是一个值得关注的前沿方向。

Slim Fly 通过网络图论中的 Moore 边界（Moore Bound） 这一极限来指导其数学构造，从而在给定路由器度数（即每个路由器的端口数）的前提下，逼近理论上可能实现的最小网络直径 。其核心在于，它并非直接使用凯莱图或强正则图，而是采用了另一类能逼近 Moore 边界的图（如 MMS 图），这些图与强正则图类似，都具有高度的对称性和优良的组合性质。下面我们通过一个表格和具体解释来说明其数学构造如何保证直径的理论最优性。

数学概念	在 Slim Fly 构造中的角色	对网络直径最优性的保证
度-直径问题	定义了设计目标：在给定路由器度数 `k`和网络直径 `D`的约束下，最大化网络能连接的终端节点数量 `N`。	明确了优化方向，即寻找在给定 `k`和 `D`下能使 `N`最大化的图结构，此时的直径 `D`对于该 `k`和 `N`而言是理论最优的。
Moore 边界	提供了节点数量 `N`的理论上限。例如，当目标直径 D=2 时，Moore 边界规定最大节点数 Nmax≈k2。	为"理论最优性"提供了绝对尺规。任何网络的规模都无法超越此边界。Slim Fly 使用的图（如 MMS 图）的节点数非常接近这个上限。
MMS 等图的构造	提供了一类具体的、可构造的图，这些图具有已知的度数 `k`和直径 `D`，并且其节点数接近 Moore 边界。	通过具体的数学构造方案，实例化了接近理论极限的网络拓扑。这使得 Slim Fly 能用较少的链路（低度数）连接大量节点，并确保任意两点间通信最多只需经过非常少的跳数（低直径）。
图的高度对称性	MMS 等图通常具有类似强正则图的对称性，即任意两个相邻节点（或非相邻节点）具有相同数量的公共邻居。	这种对称性保证了网络没有性能瓶颈和单点热点，使得负载能均匀分布 across 全网，从而在实践中也能实现理论上的低延迟和高带宽。

核心机制：逼近 Moore 边界

Moore 边界是图论中的一个经典概念，它回答了"在不超过既定直径的前提下，一个网络最多能有多大？"这个问题。Slim Fly 的设计哲学正是直接瞄准这个理论极限。其数学构造流程可以概括为：

设定目标：首先确定网络的设计目标，例如，要构建一个直径 D=2的大规模网络。
依据边界计算规模：根据 Moore 边界公式 N≈k2（对于 D=2），计算出使用特定端口数 k的路由器所能支持的最大理论节点规模。
寻找最优图：寻找或构造一种图，其度数正好是 k，直径正好是 2，并且其节点数 N尽可能接近 k2。MMS 图就是这样一类经过数学证明的、能出色逼近 Moore 边界的图。
实例化为网络：将这种图的顶点映射为网络中的路由器，边映射为路由器间的链路，就得到了 Slim Fly 网络拓扑。

通过这一过程，Slim Fly 的构造从数学上就保证了其直径是对于给定设备端口数和网络规模而言接近最优的。例如，研究表明，使用 108 端口的商用交换机构建的 Slim Fly 网络，可以支持近 20,000 个端点，而网络直径仅为 2。

强正则图的启示与联系

虽然 Slim Fly 主要采用 MMS 图进行构造，但其追求低直径的思想与强正则图 一脉相承。一个著名的强正则图例子是 Petersen 图，它具有 10 个节点，每个节点度为 3，直径为 2。Petersen 图本身规模很小，但其优美的对称性和最优性启发了广义 Petersen 图等网络模型的研究，用于构建更大规模的互连网络。Slim Fly 可以看作是这种思想在高阶图（节点数远多于 Petersen 图）上的推广和实践，其本质是运用了更深刻的数学工具来求解度-直径问题，从而实现了在大规模下的直径最优性。

总而言之，Slim Fly 架构网络直径的理论最优性并非偶然，而是其底层数学构造------基于能逼近 Moore 边界 的图（如 MMS 图）------的必然结果。这种构造方法确保了在硬件成本（由路由器端口数决定）和网络性能（由通信延迟，即直径决定）之间达到了一个近乎极致的平衡。

从对偶图视角分析，DDC（Distributed Disaggregated Chassis）架构的轨道化设计通过重构网络拓扑的本质连接关系，显著优化了AI训练中All-Reduce通信模式的延迟、带宽利用率和容错性。其核心在于将物理网络的组织方式转化为在对偶图上更优的连通结构，从而匹配All-Reduce的通信特性。以下是详细分析：

DDC轨道化设计与对偶图映射

轨道化设计本质 ：DDC架构将传统机框解耦为独立的盒式单元（如NCP、NCF），并采用"轨道"概念组织网络。具体来说，多个服务器上相同序号的GPU网卡被连接到同一个ToR（Leaf）交换机，形成一个"轨道"（Rail）。整个网络因此被划分为多个并行轨道，每个轨道内部实现高速互联（如通过NVLink），轨道间通过Spine交换机通信。
对偶图视角的转换：在对偶图中，网络设备（交换机）被视为节点，设备间的连接视为边。DDC的轨道化设计在对偶图中体现为：
- 形成高度模块化的子图：每个ToR交换机及其连接的GPU构成一个局部完全子图（Clique），代表一个轨道。这些轨道子图通过Spine交换机（对偶图中的"超节点"）互联。
- 降低对偶图直径 ：由于轨道内通信仅需1跳（经由ToR），轨道间通信最多2跳（ToR→Spine→ToR），整个对偶图的网络直径被压缩到极低水平（通常为2）。这与理想的小世界网络特性接近。

如何优化All-Reduce通信？

All-Reduce操作需要所有节点参与数据聚合与同步，其性能严重依赖网络拓扑的路径多样性和延迟。DDC的轨道化设计通过以下机制实现优化：

优化维度	对偶图上的表现	对All-Reduce的收益
局部性优先	轨道内的ToR交换机及其连接设备形成密集连接的子图（团结构）	All-Reduce可优先在轨道内完成局部聚合（如Reduce-Scatter阶段），减少跨轨道流量，降低Spine层负载。
路径多样性	Spine交换机在对偶图中作为高阶连接点，提供轨道间多路径	进行全局同步时，流量可通过多个Spine并行传输，避免单路径拥塞，充分利用等价多路径（ECMP）。
延迟优化	对偶图直径小（2跳），节点间通信距离短	显著降低同步延迟，尤其对于All-Reduce中关键的全局归约步骤。

具体通信流程优化：
- 阶段1（轨道内Reduce）：每个轨道内的GPU首先在本地ToR下完成部分梯度聚合。由于轨道内带宽高且延迟低，此阶段快速完成。
- 阶段2（轨道间All-Reduce）：局部聚合结果通过Spine层在轨道间进行全局同步。Spine层的高带宽和多路径保障了全局操作的效率。
- 整体效果 ：这种分层操作减少了全局通信的数据量，并通过并行化降低了端到端延迟。

容错性与负载均衡的增强

容错性 ：在对偶图中，单个轨道或Spine链路的故障仅影响局部子图。DDC架构支持快速故障检测与路径切换（如DPSH技术），故障轨道内的流量可瞬时重路由到其他健康轨道，避免All-Reduce中断。
动态负载均衡 ：DDC的FGLB（灵活全局负载均衡）技术允许Spine设备监控远端链路负载，并动态调整ECMP权重。在对偶图层面，这相当于根据实时流量优化边权重，避免部分超节点（Spine）过载，确保All-Reduce流量均匀分布。

理论依据：与ZCube拓扑的类比

DDC的轨道化设计与新型拓扑ZCube（见）理念相似。ZCube通过数学构造（如利用凯莱图）实现低直径和高容错性，其在对偶图上的模块化组织与DDC的轨道化设计异曲同工：

ZCube通过分层交换机构建维度化的连接，使All-Reduce等操作可沿不同维度并行执行。
DDC的轨道本质上是一种简化的、工程友好的实现，同样旨在优化集合通信的拓扑基础。

总结

总而言之，从对偶图视角看，DDC架构的轨道化设计通过将网络组织为多个局部高连通子图（轨道），并由高阶节点（Spine）高效互联 ，构建了一个逼近理论最优的网络拓扑。这种结构显著优化了All-Reduce通信的局部性、路径多样性和延迟，同时通过动态负载均衡和快速容错机制保障了稳定性。这使DDC特别适合大规模AI训练场景，其中All-Reduce是性能关键路径。

1.3.4 纠删码技术在跨数据中心数据同步中的作用、数据中心容灾中的应用

纠删码技术在跨数据中心数据同步中，主要通过其独特的编码方式和数据放置策略来优化带宽消耗。下面这个表格可以帮你快速对比它与多副本方案的核心差异。

特性维度	多副本方案 (如三副本)	纠删码技术 (以RS(10,4)为例)
带宽消耗原理	需同步完整的多个数据副本	将数据编码分割成多个数据块和校验块
跨中心同步流量	高 (例如，三副本需额外传输200%的数据量)	较低 (仅需传输数据块和少量校验块，总流量远低于多副本)
存储效率	低 (磁盘利用率仅为1/副本数，如三副本约为33%)	高 (磁盘利用率通常可达70%以上，如10+4配置利用率约为71%)
数据恢复带宽	较低 (只需完整拷贝一个现存副本)	较高 (需从多个节点读取数据块和校验块进行解码计算)
计算开销	几乎无 (简单数据复制)	高 (涉及复杂的编码/解码计算，消耗CPU资源)
适用场景	热数据、对写入延迟和恢复速度要求高的场景	温/冷数据、对存储成本敏感、数据体量巨大的场景

纠删码如何节省带宽

纠删码技术之所以能在跨数据中心的场景下显著节省带宽，主要依赖于以下几个核心机制：

数据切片与编码

纠删码技术将一份完整数据分割成k个数据块 ，然后通过数学算法（如Reed-Solomon码）计算出m个校验块，总共生成n=k+m个数据块。在跨数据中心同步时，无需同步整个数据的多个完整副本，而是将这些数据块和校验块分散到不同的数据中心。恢复数据时，只要任意k个块存活，就能还原出原始数据。这意味着同步网络流量从多副本的数倍数据量，降低为仅需传输这些数据块和校验块。
局部校验与智能布局

为了进一步优化跨数据中心的带宽消耗，特别是数据恢复时的流量，出现了如LRC（局部校验码） 等更高级的纠删码。LRC在全局校验块之外，还会为一部分数据块生成局部校验块。这样，当某个数据块丢失需要修复时，有很大概率只需在同一个数据中心或区域网络内，利用局部校验块和存活的数据块完成修复，从而避免了昂贵的跨数据中心带宽消耗。
数据放置与传输优化

优化的数据放置策略对降低带宽消耗也至关重要。研究提出了通过建模优化数据块的放置策略，综合考虑用户访问延迟和数据恢复时的传输延迟。例如，将访问频率高的"热"数据块放置在更靠近用户的数据中心，同时保证数据块分布能满足高效恢复的需求。此外，像数据归并传输（将多个小数据对象的备份请求打包成一个大数据包再传输）这样的策略，可以有效减少跨数据中心网络传输中小数据包带来的高昂延迟和协议开销，从而提升带宽的有效利用率。

如何选择适合的方案

选择多副本还是纠删码，关键在于平衡您的业务需求。

追求极致性能与低延迟 ：若您的业务涉及频繁访问的热数据 （如在线交易系统、实时分析），且对I/O延迟和快速恢复有极高要求，多副本方案更具优势，因为它能提供更低的读写延迟和更快的恢复速度。
关注成本与海量数据 ：若您需要存储的是温数据或冷数据 （如备份归档、大数据分析的历史数据），数据体量巨大且对存储成本敏感，纠删码技术是更经济的选择，它能以更低的存储开销提供更高的数据可靠性。

纠删码的编码和解码计算开销对业务性能的影响确实非常显著，尤其是在高吞吐或高并发的场景下。下面这个表格通过一个对比测试，可以让你对计算开销的影响有个直观的感受。

性能维度	低冗余场景 (如 RS(10,1))	高冗余场景 (如 RS(6,6))	说明
编码吞吐量	极高 (可达 3500 MB/s以上)	急剧下降 (可低至 200 MB/s以下)	生成校验块越多，计算越复杂，速度越慢。
解码吞吐量	较高 (可达 2000 MB/s以上)	较低 (可低至 140 MB/s)	数据块丢失越多，需要恢复的计算量越大，速度越慢。
CPU 占用率	较低	显著增高 (可达60%或更高)	复杂的编解码运算会大量消耗CPU计算资源。
写惩罚	较低 (如 RS(4,1) 为4)	很高 (如 RS(4,2) 为6)	单次数据写入需触发多次磁盘I/O和计算，放大I/O压力。

计算开销从何而来？

纠删码的计算开销主要源于其数学本质。它不是简单复制数据，而是通过矩阵乘法 等算法（如在伽罗华域上的运算）将 k个原始数据块计算出 m个校验块。这个过程可以简单理解为解一个复杂的多元一次方程组。

冗余度是关键因素 ：上表中性能的巨大差异，核心原因就是冗余度。m值（校验块数量）越大，需要计算的校验数据就越多，矩阵运算越复杂，导致CPU计算量急剧增加。例如，RS(10,2)的编码吞吐量远高于RS(6,6)，因为后者需要生成更多的校验块。
算法优化的作用 ：为了降低开销，业界不断优化算法。例如，原始的范德蒙RS编码 计算复杂度高，而改进后的柯西RS编码通过将运算转换到二进制域，利用异或操作代替部分复杂运算，能大幅提升编解码速度。在一些测试中，优化后的柯西编码吞吐量可以是原始范德蒙编码的5倍以上。

权衡的艺术：存储效率 vs. 计算性能

选择纠删码本质上是用计算资源 和写入延迟 去换取存储空间。这种权衡在以下业务场景中需要特别考量：

海量温冷数据存储 ：这是纠删码的"主战场"。适用于视频、图片、备份归档等访问频率低但体量巨大的数据。这些场景对读取延迟不敏感，存储成本是首要考虑因素，纠删码以计算开销换取高得盘率的优势得以充分发挥。
高性能热数据存储 ：对于数据库、在线交易系统 等要求低延迟、高IOPS的业务，**多副本（Replication）** 通常是更佳选择。因为多副本的读写路径更直接（近乎零计算开销），性能更高，故障恢复速度也快得多。
写密集型业务：需要重点关注纠删码的"写惩罚"。一次数据写入会引发多次I/O和计算，可能成为性能瓶颈。如果业务是写密集型的，需要评估集群的CPU和I/O负载能力。

如何优化与选型？

在实际应用中，可以通过以下策略来优化和决策：

数据分层存储：采用"热-温-冷"数据管理策略。热数据用多副本，确保性能；温冷数据迁移到纠删码池，节约成本。
利用硬件加速 ：采用支持Intel ISA-L等专用指令集的CPU，可以极大加速编解码过程。现代分布式存储系统（如Ceph, HDFS）都已支持这类优化。
针对性测试 ：理论数据仅供参考，最终决策必须基于实际业务数据的测试。在你的硬件环境和典型工作负载下，测试不同纠删码策略（如RS(6,3)、RS(8,4)）的实际吞吐量和延迟，看是否能满足业务SLA（服务等级协议）。

总而言之，纠删码的计算开销是真实存在且不可忽视的，它会直接转化为更高的CPU占用和更长的请求延迟。决策的关键在于精准判断你的业务属于哪种类型：

若业务追求极致的存储成本效益 ，且能接受一定的性能代价，纠删码是理想选择。
若业务追求极致的性能和低延迟 ，多副本是更稳妥的方案。

最佳实践往往是混合使用这两种策略，并根据数据的重要性、访问频率动态调整，从而实现成本与性能的最佳平衡。

高并发小文件场景下的问题

在高并发小文件场景下，标准配置的纠删码技术确实会面临性能挑战，但通过一系列巧妙的优化策略，可以有效改善其表现。下面这个表格汇总了核心的性能瓶颈与相应的优化方向，希望能帮你快速建立起整体认知。

性能维度	纠删码的挑战 (小文件场景)	核心优化目标
写入性能	写放大严重：一个小文件也需编码成K+M个数据块，分散写入多个节点，产生大量小IO。	减少写入IOPS，避免直接在线EC写入。
读取性能	读放大严重：读取任何小文件，都需要从至少K个节点成功获取数据块并解码，延迟高且易受慢节点影响。	优化读取路径，减少网络交互和解码开销。
元数据压力	元数据爆炸：海量小文件产生海量元数据，对元数据服务器的查询和管理造成巨大压力。	设计高效的元数据管理系统，并合并小文件。
存储利用率	条带利用率低：小文件可能无法填满一个条带，造成存储空间浪费。	提高单次写入的数据量，提升条带利用率。

纠删码的本质是将数据切成K个数据块，并计算生成M个校验块，然后将这K+M个块分散存储。对于一个大文件，这种分布式的读写能充分利用多节点带宽。但对于小文件，这种机制却成了性能"杀手"。

写入瓶颈 ：想象一下，一个1MB的小文件，如果采用RS(6,3)策略（即9个块），它需要被切分、编码，然后发起9次网络写入。这相当于为了存储1MB有效数据，系统实际要处理9次I/O操作，写放大非常严重。
读取瓶颈与长尾延迟 ：读取时更麻烦。系统必须从9个节点中成功取回任意6个块，才能解码出原始文件。只要有一个节点响应慢，整个读取请求就会被拖慢，这就是所谓的长尾延迟问题，在高并发下会急剧放大。
计算开销：高频的编解码运算会给CPU带来持续压力。

纠删码核心优化策略

针对以上痛点，业界提出了几种有效的优化思路。

元数据与管理优化

海量小文件带来的海量元数据是首要瓶颈。优化方向包括采用分布式元数据服务（如基于Raft协议构建）来取代单点元数据管理，并将元数据存储在SSD上以加速访问。

数据组织与IO优化

这是提升性能的关键，核心思想是 "化零为整"。

小文件合并 (Object Merging) ：这是最核心的优化之一。系统在写入时，不再将每个小文件直接进行EC编码，而是先将一段时间内的多个小文件在内存或缓存中拼接成一个更大的逻辑对象（例如几MB或几十MB），再对这个大对象执行EC条带化写入。这样做的好处是：
- 大幅减少IOPS：将N次随机小IO合并成一次顺序大IO。
- 提高条带利用率：使每个EC条带都被有效数据填满。
- 降低元数据数量：多个小文件合并后，可能只对应一份EC条带的元数据。
智能条带放置策略 ：为了优化读取，在合并小文件时可以采用更智能的放置策略。例如，纵向条带搁置策略会尽量让单个小文件的数据块集中在少数几个节点上。这样在读取这个文件时，可能只需访问1-2个节点而非K个节点，极大地减少了网络交互，降低了读取延迟和长尾风险。
备份请求 (Backup Request)：为应对读取时的慢节点问题，可以在发起读取请求时，同时向超过K个（例如K+1或K+2个）节点请求数据块。无论哪K个块先返回，都立即开始解码并响应应用，从而有效抵消个别节点高延迟的影响。

系统架构优化

分层存储/离线EC (Offline EC) ：对延迟极其敏感的在线写入，可以采用折中方案。数据先高速写入一个多副本缓存层 （如SSD），快速响应客户端。然后，后台有异步任务将缓存层的数据批量合并、转换为EC编码，再存入持久化的EC存储池。这用空间换取了时间，实现了写入性能和经济性的平衡。
Quorum写入机制 ：在线EC写入时，不要求所有K+M个块都写入成功才返回。可以设定一个法定数量（如K+1个块写入成功），就向应用报告写入成功。失败的数据块由后台进程异步修复，这能显著提升写入请求的成功率和降低延迟。

总结与建议

总而言之，面对高并发小文件场景，直接使用原生纠删码通常不是最佳选择 。但其通过 **"合并写入、智能放置、缓存加速、异步转换"** 等优化策略后，纠删码系统完全可以胜任此类场景，并在存储成本和控制长尾延迟方面取得良好平衡。

选择建议：

若您的业务纯粹追求极致的读写延迟和吞吐量 ，且对存储成本不敏感，多副本方案仍是更简单直接的选择。
若您的业务数据体量巨大 ，对存储成本敏感 ，同时能够接受经过优化后依然略高于多副本的延迟（尤其是在读路径上），那么采用上述优化策略的纠删码方案是非常经济的选择，特别适用于图片、短视频、日志文件等温冷数据的存储场景。

纠删码技术在分布式存储系统中，确实需要根据不同的数据规模、访问模式和性能要求来灵活调整策略。

数据场景类型	典型数据规模与访问特点	纠删码核心策略	性能表现与优化重点
海量小文件/元数据	文件尺寸小（如小于128KB），数量极多，随机读取为主，要求低延迟和高TPS（每秒事务数）。	小对象合并、非系统化MSR编码、纵向条带搁置、离线批处理。	写放大和读放大是主要挑战。通过合并小文件为逻辑大对象再编码，大幅减少IOPS；通过优化数据局部性，使多数读取能在少数节点完成，降低延迟。
大文件/流式数据	文件尺寸大（如GB级以上），顺序读写为主，追求高吞吐带宽（Throughput）。	系统化MSR编码、横向条带搁置、大条带参数（如16+4）。	性能瓶颈主要在网络带宽和磁盘顺序IO能力。条带化写入能充分利用多节点带宽。关注点在于降低跨数据中心同步的流量和提升数据修复效率。
混合负载/在线服务	数据规模与类型混合，要求兼顾读/写延迟（Latency）与吞吐量，保证服务稳定性。	数据分层（热数据多副本+温冷数据EC）、参数自适应、Backup Request机制、异构集群感知。	核心是平衡与稳定。通过自适应算法为不同文件选择最佳EC参数；采用备份请求抵御慢节点引发的长尾延迟；在异构硬件环境中智能放置数据以实现负载均衡。

性能表现与优化策略探析

纠删码的性能挑战根源于其机制：数据被分片编码并分散存储，任何读写操作都可能涉及多个节点。

小文件场景的挑战与优化

小文件场景下，每个文件都可能触发一次完整的EC编码和跨网络写入，产生巨大的写放大 。读取时，即使获取一个极小文件，也可能需要从多个节点读取数据块进行解码，导致读放大 和长尾延迟。

优化策略核心是"化零为整"。小对象合并（Object Merging） 是将多个小文件在逻辑上打包成一个大对象再进行EC编码，从而将大量随机小IO转化为少量顺序大IO。纵向条带搁置（Contiguous Placement） 策略则尽可能让单个小文件的数据集中在少数节点上，多数读取操作只需访问1-2个节点即可完成，显著降低了网络交互和延迟。对于延迟敏感性极高的在线写入，可采用 **"离线写在线读"** 架构，数据先写入高性能的多副本缓存层，再由后端服务异步合并、转换为EC格式，实现性能与成本的平衡。
大文件场景的挑战与优化

大文件场景追求高吞吐。横向条带搁置（Stripe Placement） 策略将文件数据顺序切分后分布到大量节点上，写入和读取时可以并行利用所有节点的聚合带宽，非常适合流式数据传输。此时，选择较大的K、M值（如10+4，16+6）能获得更高的存储利用率，但需注意，过大的K值会在节点故障时增加修复带宽和数据不可用时间。对于跨数据中心的容灾，**LRC（局部校验码）** 等高级编码方案能在局部区域内完成大部分数据修复，极大减少昂贵的跨数据中心带宽消耗。
混合负载场景的挑战与优化

混合负载场景要求系统具备弹性和智能。基于CRITIC客观权重法的参数自适应选择 是一类先进方案，它通过数学模型综合评估文件大小、可靠性目标、存储成本等多个性能指标，动态为每个文件或每类数据选择最优的EC参数（K, M），实现全局最优权衡。备份请求（Backup Request） 机制是应对长尾延迟的有效手段，当向某个节点请求数据超时，可同时向其他存有相同数据块的节点发送备份请求，取最快返回的结果，从而有效屏蔽慢节点的影响。在硬件异构的环境中，异构感知数据放置策略 将性能相近的节点分组，确保一个EC条带内的数据块尽可能分布在同一组内，避免木桶效应，提升任务执行效率。

数据中心级容灾设计要点

在数据中心级别部署纠删码容灾方案，需从全局视角规划数据分布与修复流程。

数据放置与风险感知 ：简单的跨数据中心均匀分布数据块并非最优。先进的策略会引入风险感知，综合考虑地理分布的灾害风险对数据中心和通信链路的影响，建立数据安全放置的数学模型。目标是避免将所有数据块放置在同一个高危区域，而是分散在风险概率较低且相对独立的故障域中，从而在灾备层面降低数据整体丢失的风险。
修复流程的优化 ：当某个数据中心或大量节点同时故障时，高效的修复机制至关重要。传统逐块修复方式会产生巨大网络流量。优化方案如**高效修复树（ERT）** 被提出，通过在修复过程中尽早使数据块在网络中间节点进行智能合并（如异或操作），显著减少修复流量的传输。同时，采用动态调整修复树根节点的策略，能更好地适应网络拓扑，实现负载均衡，加速整体修复过程。
系统架构与硬件加速 ：在系统层面，可以采用扁平化数据中心存储架构 ，认为在网络带宽足够高的前提下，数据的局部性不再是最关键因素，存储与计算可分离。同时，利用Intel ISA-L等专用指令集库对编解码过程进行加速，能极大降低CPU开销，这对于处理大量数据的场景性能提升非常关键。

核心原则总结

选择与优化纠删码策略，本质上是持续在存储效率、性能、可靠性之间进行权衡。核心原则可总结为：

小文件 ：首要目标是降低IOPS放大和延迟，核心思路是合并与缓存。
大文件 ：首要目标是最大化吞吐量和修复效率，核心思路是条带化并行和智能编码。
混合负载 ：首要目标是实现智能均衡与稳定，核心思路是自适应、感知环境和冗余请求。

风险感知数据放置模型的具体实现方法

这类模型的核心目标，是将数据智能地放置在最能支持其风险识别与预警功能的位置，这通常涉及对数据来源、特征、关联关系的系统化处理。

任何数据放置模型的第一步都是理解数据。以监控大型工业设备（如风机、水泵）的振动信号为例，我们需要定义数据的层次和风险指标：

原始数据层：直接从传感器采集的、带有时间戳的连续振动信号。
特征指标层：从原始信号中提取的、与设备健康状态相关的关键指标，例如：
- 时域特征：有效值（RMS，反映总体振动能量）、峰值（反映冲击性故障）、偏度/峭度（反映信号分布形状，对早期损伤敏感）。
- 频域特征：通过傅里叶变换得到的频谱，可以识别特定频率成分（如轴承的故障特征频率、齿轮的啮合频率），这是诊断故障类型的核心依据。
风险标签层：基于特征指标和历史经验设定的阈值或模型输出，为数据打上标签，如"正常"、"预警"、"报警"。

🧠 核心：三种典型的数据放置模型实现路径

基于上述数据层次，我们可以选择不同的技术路径来构建数据放置模型。

参数化规则模型 (适用于机理明确、规则清晰的场景)

这种方法的核心是 **"如果...那么..."** 的专家规则。它将领域知识（如设备维护手册中的振动标准）固化为可执行的逻辑。

实现举例：
- 数据放置策略 ：将振动峰值 和轴承故障特征频率的幅值这两个关键特征指标，存储在高速时序数据库中，以便实时计算和规则判断。
- 模型规则：
  - IF振动RMS值 > 7.1 mm/s AND峭度指标 < 3.5 THEN状态 = "预警"，数据流向 = "预警数据库"并触发工单系统。
  - IF频谱中检测到轴承外圈故障特征频率 THEN状态 = "报警"，数据流向 = "高优先级报警队列"并通知维护工程师，同时将完整的原始波形数据归档至"故障案例库"以供深度分析。

这种方法逻辑清晰、解释性强，非常适合机理明确的常规故障。但当设备增多、故障模式复杂后，维护成千上万条规则会变得非常困难。

机器学习判别模型 (适用于从数据中学习复杂模式的场景)

当故障征兆与正常运行状态差异微小，难以用简单规则描述时，机器学习模型可以自动从海量历史数据中学习出正常的"模式"，并识别出偏离该模式的异常。

实现举例：
- 模型选择与训练 ：使用隔离森林（Isolation Forest） 或**一类支持向量机（One-Class SVM）** 等无监督异常检测算法。模型使用设备正常运行时的大量振动特征数据（如RMS、峰值、多频段能量等）进行训练，学习"健康"的数据分布。
- 数据放置策略 ：将所有用于模型推理的特征指标 放置在模型的输入侧特征库 中。当模型判定某个设备的数据点为"异常"时，该设备的所有相关数据（包括原始波形）会被自动标记并**放置到"嫌疑故障数据池"** 中，供专家进行复核和诊断。

这种方法能发现人难以定义的复杂异常模式，但模型决策过程如同"黑箱"，解释性较差。

知识图谱关联模型 (适用于需要理解全局关联性的场景)

对于复杂系统，单一设备的故障可能引发连锁反应。知识图谱擅长表达"实体"和"关系"，能将分散的风险信息连接成一张全局网络。

实现举例：
- 图谱构建 ：以设备（如"水泵A"）、部件（"轴承B"）、传感器（"振动传感器S1"）、测点、报警事件等为节点。以它们之间的关系（"隶属于"、"安装于"、"采集自"、"曾发生"）为边，构建知识图谱。
- 数据放置策略 ：当传感器S1产生报警时，系统不仅查看S1的数据，还会通过知识图谱自动关联查询：
  - 与水泵A通过同一管道连接的"水泵C"和"阀门D"最近是否有异常？
  - 轴承B的历史维修记录 和同类设备的故障案例有哪些？
- 所有被关联到的实体数据，会被动态地、临时性地"放置"在一个统一的分析视图中，帮助分析人员快速定位根本原因。

这种方法极大地增强了风险情境的感知能力，能够揭示隐藏的依赖关系和传播路径，实现从"点状预警"到"全局洞察"的飞跃。

💡 如何选择与融合使用？

在实际应用中，通常不会只采用一种模型，而是根据需求进行组合：

追求快速响应和明确规则 时，可首选参数化规则模型。
需要检测未知故障或复杂模式 时，可结合机器学习判别模型。
当系统复杂、需要理解风险的全景和关联 时，知识图谱关联模型能提供更深入的洞察。

这三种模型也常常协同工作，例如，用规则模型进行实时阈值判断，用机器学习模型进行周期性深度扫描，最后将所有报警和资产信息用知识图谱进行关联分析，形成一套层次化的风险感知数据管理体系。

平衡纠删码参数 (K, M) 与容灾指标（RTO/RPO）

在实际部署中，平衡纠删码参数 (K, M) 与容灾指标（RTO/RPO）是一个核心的架构决策。下面这个表格清晰地展示了这种权衡关系，可以帮助你快速把握核心思路。

关键指标	偏向高可用性/低延迟 (低RTO/RPO)	偏向存储效率/成本优化	内在权衡逻辑
数据冗余量 (M)	倾向较大的M值 (如4或6)，以容忍多个节点或整个机架甚至数据中心故障。	倾向较小的M值 (如2或3)，以减少存储开销和网络传输量。	M ↗ → 可靠性↗，跨数据中心带宽消耗↗，写入延迟可能↗。
数据块数量 (K)	倾向较小的K值。单个数据块较大，修复时需读取的节点数少，解码计算量小，能加快恢复速度。	倾向较大的K值。有利于提高存储效率（冗余度 = (K+M)/K），K越大，效率越高。	K ↗ → 存储效率↗，但单点故障需联系更多节点（K个）修复，恢复时间可能延长。
典型应用场景	核心交易库、实时在线服务。常采用多副本+纠删码分层或LRC码。	备份归档、大数据分析、温冷数据存储。可采用RS码并设置较大的K值。	需要在业务连续性与存储成本之间找到最佳平衡点。

深入理解权衡机制

表格中的关系源于纠删码的工作原理。RPO（恢复点目标）衡量数据丢失量，主要由数据保护频率决定。而RTO（恢复时间目标）衡量服务恢复速度，在纠删码场景下，受以下因素显著影响：

恢复带宽 ：当发生故障，需要修复或重建数据时，传统RS码需要从至少 K 个存活节点读取数据。如果K值很大，就意味着需要传输更多的数据，这会直接拉长恢复时间，不利于实现低RTO。
局部修复能力 ：这是优化RTO的关键。像LRC码 这样的编码方式，通过创建局部校验组 ，使得当组内单个数据块丢失时，只需从组内少数几个节点读取数据即可恢复，而无需联系所有的K个节点。这极大地减少了修复时的网络传输量，从而显著降低了数据恢复的延迟，有助于实现更低的RTO。
计算开销：编解码过程需要CPU计算。在恢复时间紧迫的情况下，巨大的计算量可能成为瓶颈。因此，选择计算效率更高的编码库（如Intel ISA-L）或利用硬件加速（FPGA）对满足低RTO至关重要。

容灾场景下的参数配置策略

基于以上理解，可以形成以下部署策略：

为不同数据分级设定策略

这是最有效的方法。不要试图用一种配置满足所有需求。
- 热数据 (要求极低RTO/RPO) ：对性能敏感，通常采用多副本 策略。若要使用纠删码，可考虑K=4, M=2 这类小参数配置，或采用LRC码（如Azure云采用的LRC），将局部组设置在同一机架内，实现快速修复。
- 温数据 (平衡成本与性能) ：可采用标准的RS码，例如RS(6,3) 或 RS(10,4)。这样在存储效率和恢复时间之间取得了较好平衡。
- 冷数据/归档数据 (成本优先) ：主要目标是降低存储开销，可以容忍较长的RTO。此时可采用**RS(14,10)** 或更大的K值，以追求极高的存储效率。
跨数据中心容灾的特殊考量

在跨数据中心的场景下，网络带宽通常是昂贵且有限的稀缺资源。
- 优化跨中心流量 ：采用LRC码，并将局部校验组与单个数据中心对齐。这样，当某个数据中心内发生单块故障时，修复流量被限制在该数据中心内部，避免了昂贵的跨数据中心带宽消耗，这对保护RPO和降低成本非常关键。
- 利用WAN加速技术：结合数据压缩、重复数据删除等技术，减少实际需要同步的数据量，间接优化恢复时间。
利用现代编码技术优化
- 局部修复码 (LRC)：如前所述，LRC通过牺牲少量存储空间（增加局部校验块）来换取修复速度的极大提升，是平衡RTO和存储效率的利器。
- 持续数据保护 (CDP)：对于RPO要求极高的核心系统，纠删码可与CDP技术结合。CDP近乎连续地捕获数据变化，实现近乎零的RPO；纠删码则作为底层的经济存储方案。

核心总结

总而言之，纠删码参数(K, M)与RTO/RPO的平衡，本质上是存储效率、计算资源、网络带宽与业务连续性要求之间的权衡。

决策时，最关键的步骤是对数据进行分级 ，并为不同级别的数据制定明确的RTO/RPO目标。然后，基于这些目标去选择最合适的纠删码类型（如RS、LRC）和参数。在跨数据中心场景下，重点考虑LRC等能减少跨域流量的方案，并充分利用硬件加速和WAN优化技术。

存储系统的容灾规划中：RAID（独立磁盘冗余阵列）与纠删码（Erasure Coding）

在存储系统的容灾规划中，RAID（独立磁盘冗余阵列）与纠删码（Erasure Coding）是两种核心的数据保护技术。它们分别适用于不同的场景，共同构建了从单机到分布式系统的多层次容灾体系。

下面这个表格直观地对比了它们在容灾规划中的关键特性，帮助您快速把握核心差异。

特性维度	RAID (冗余磁盘阵列)	纠删码 (Erasure Coding)
冗余机制	主要在单节点或磁盘阵列内部通过镜像或奇偶校验实现冗余。	跨节点/机架/数据中心，将数据分块编码后分散存储。
容错粒度	通常针对磁盘故障（如RAID 5容忍1块盘故障，RAID 6容忍2块盘故障）。	可针对节点故障、机柜故障甚至数据中心级故障，容错能力由编码参数决定（如"8+2"配置可容忍2个组件故障）。
存储效率	相对较低（例如，RAID 1的存储利用率仅为50%，RAID 5约为(N-1)/N）。	更高（例如，与三副本相比，采用RS编码可能仅需1.5倍存储空间即可实现相当的容错能力）。
典型应用场景	本地存储、数据库服务器、对低延迟和高性能要求高的关键业务。	云存储、大数据平台（如Hadoop、Ceph）、海量温冷数据存储，优先考虑存储成本效益。

💡 规划要点：如何选择与结合使用

在实际的容灾系统规划中，RAID和纠删码并非互斥，而是常常协同工作。

数据分层策略是关键

根据数据的热温冷属性采用不同的保护机制是通用最佳实践。
- 热数据（访问频繁） ：对性能要求极高，通常建议采用多副本 或高性能的RAID 10（RAID 1+0）。在分布式系统中，新写入的热数据也可先采用多副本策略，再异步转换为纠删码。
- 温/冷数据（访问频次低） ：对存储成本敏感，非常适合采用纠删码技术，如Ceph中常见的"8+2"、"10+4"等配置。这能在保证可靠性的前提下显著提升存储空间利用率。
关注恢复速度与"写惩罚"
- 恢复时间：RAID在重建大容量故障磁盘时可能耗时较长。纠删码的数据修复需要读取较多数据块并进行解码计算，会占用网络和CPU资源。规划时需评估并确保恢复速度能满足业务连续性要求（RTO）。
- 写惩罚：RAID 5/6等级别在写入数据时需更新奇偶校验信息，会产生"写惩罚"，影响随机写入性能。纠删码的数据更新过程也相对复杂。在写入密集型场景下，这一点需要重点考量。
利用先进编码技术优化

为了克服标准纠删码（如RS码）在修复开销方面的不足，可以采用更先进的编码方案。例如，**LRC（局部校验码）** 通过增加局部校验块，使得大部分数据修复操作能在系统局部完成，大幅减少了跨节点或跨机柜的数据传输量，有效降低了修复带宽和延迟。

🛠️ 实施建议

明确业务需求：首先定义关键业务的RPO（恢复点目标）和RTO（恢复时间目标）。例如，医院核心系统（HIS）可能追求RPO=0和RTO≈0，这需要通过双活数据中心等架构来实现。
硬件与软件选型：对于RAID，选择支持所需RAID级别且带有电池保护缓存的高质量硬件RAID卡，有助于提升性能与可靠性。对于纠删码，选择成熟稳定的分布式存储软件（如Ceph）至关重要。
监控与维护：建立完善的监控系统，实时监控RAID阵列健康状况和分布式存储集群的存储池状态。制定定期的数据备份和容灾演练计划。

混合云环境中RAID 与纠删码组合使用

在混合云环境中，将 RAID 与纠删码组合使用，核心目标是平衡性能、成本、可靠性和可扩展性。下面这个表格清晰地展示了它们在不同场景下的角色与协作方式，可以帮助你快速掌握核心策略。

存储层级/数据类型	核心目标	推荐技术组合	部署位置与说明
热数据 (高频访问)	极致性能与低延迟	RAID (如10/50/60) 或多副本	私有云/本地数据中心。为保证关键应用（如数据库）的响应速度，采用硬件RAID卡或基于NVMe的RAID卸载技术，将计算开销从主机CPU卸载。
温数据 (中低频访问)	性能与成本的平衡	纠删码 (如RS(8,4), LRC)	私有云/本地集群。用于大数据分析、内部文件共享等场景。纠删码能以较低存储开销（如1.5倍）提供高可靠性。
冷数据 (归档备份)	极致的存储成本优化	纠删码 + 公有云对象存储	公有云。将备份、归档数据迁移至支持纠删码的公有云对象存储（如AWS S3 Standard-IA/Glacier）。利用其近乎无限的扩展性和按需付费模型。

💡 策略核心：分层治理与动态流动

上述实践的成功，依赖于两个关键原则：分层治理 和动态流动。

分层治理：承认不同类型的数据有不同价值，不应采用"一刀切"的存储方案。核心交易库需要RAID提供的毫秒级延迟，而历史合规数据则优先考虑纠删码的经济性。
动态流动 ：数据的价值会随时间变化。最佳实践是建立自动化的数据生命周期管理策略。例如，可设定规则让生产数据在30天后从高性能的RAID存储池自动迁移至温数据纠删码池，一年后再归档至公有云。这确保了资源被高效利用。

🛠️ 实施路径与注意事项

将策略落地时，以下几点至关重要：

数据分类是基石 ：首先必须与业务部门协同，根据访问频率、性能要求和业务重要性对数据进行清晰分类。这是所有后续决策的基础。
利用现代硬件卸载计算开销 ：在私有云中处理热数据时，为充分发挥NVMe SSD的性能并解放主机CPU，应考虑采用新一代硬件加速技术。例如，使用专为NVMe设计的RAID卡或基于GPU的RAID协处理器，将奇偶校验计算任务卸载，从而为应用释放宝贵的CPU资源。
统一管理平面 ：理想的混合云存储方案应提供一个统一的管理界面，能够同时管理本地RAID阵列、分布式纠删码集群和多个公有云的存储资源。这能极大降低运维复杂度。
网络是隐形基石 ：混合云架构严重依赖网络连接。必须确保私有云和公有云之间有高质量、高带宽、低延迟的网络链路。对于数据同步和迁移，网络的稳定性和带宽直接决定了RTO（恢复时间目标）和RPO（恢复点目标）。

💎 总结

总而言之，RAID与纠删码在混合云中并非替代关系，而是互补伙伴。核心策略是：利用RAID保护对性能敏感的热数据，利用纠删码高效存储温冷数据，并通过自动化生命周期策略让数据在"热-温-冷"分层间自由流动，最终在整体上实现性能、成本与可靠性的最佳平衡。

1.3.5 容灾方案对业务RTO（恢复时间目标）和RPO（恢复点目标）的影响

量化评估容灾方案对业务RTO（恢复时间目标）和RPO（恢复点目标）的影响，是一个系统性的过程。它始于对业务自身的深刻理解，终于对技术方案的持续验证。下面这个表格概括了评估流程中的核心环节，希望能帮助您快速建立整体认知。

评估环节	核心任务	关键产出/量化方法
1. 业务影响分析	识别关键业务，评估中断影响，确定其固有的RTO/RPO需求。	业务系统分级（如Tier 1-4）、各业务可容忍的最大中断时间与数据丢失量。
2. 技术方案映射	将容灾技术能力（如备份、复制、多活）与业务需求进行匹配。	不同技术方案可实现的理论RTO/RPO范围（如同步复制可实现RPO≈0）。
3. 成本效益分析	量化实现特定RTO/RPO目标的投入与不达标的潜在损失。	容灾方案总拥有成本（TCO）、因停机与数据丢失造成的预期经济损失。
4. 测试与演练	通过模拟故障，实际测量方案的真实恢复能力。	实测的恢复时间、数据丢失量、成功率，并与预设目标对比。

第一步：明确业务的真实需求

任何容灾方案的起点都不是技术，而是业务。您需要先回答："如果系统中断，对业务意味着什么？" 这就是业务影响分析（BIA）。

识别关键业务系统：并非所有系统都同等重要。您可以参考行业实践，将系统分为不同等级。例如：
- Tier 1-核心交易系统 ：如支付、证券撮合引擎。中断会直接导致收入损失和重大声誉风险，要求RTO/RPO极低（如RTO<30秒，RPO=0）。
- Tier 2-重要业务系统 ：如电商订单、CRM系统。中断影响业务运营，但有一定缓冲时间，通常要求RTO/RPO在分钟到小时级。
- Tier 3-内部支持系统 ：如内部邮件、开发测试系统。中断影响效率，但可接受较长的恢复时间，RTO/RPO可达数小时或更长。
量化中断影响：与业务部门协作，估算每小时中断可能导致的经济损失（收入、违约金）、客户流失风险以及合规处罚金额。这为后续的成本效益分析提供依据。

第二步：分析容灾技术方案的影响

不同的容灾技术直接决定了RTO/RPO的天花板。下表对比了主流方案的特性：

容灾方案	典型RPO（数据丢失）	典型RTO（恢复时间）	核心技术原理	适用场景
备份与恢复	数小时 ~ 数天	数小时 ~ 数天	定期生成数据副本，恢复时完整还原。	非核心数据、归档、可接受长时间中断的系统。
异步复制	秒级 ~ 分钟级	分钟级 ~ 小时级	数据在主节点处理后，异步复制到备节点。	重要业务系统，可容忍少量数据丢失。
同步复制/双活	≈ 0	秒级 ~ 分钟级	数据必须在主备节点同时写入成功后才确认。	核心交易系统，要求零数据丢失和快速切换。
多活架构	≈ 0	秒级（甚至用户无感）	多个节点同时提供服务，故障时流量直接切至存活节点。	对连续性和扩展性有极高要求的互联网核心业务。

量化影响的关键 ：评估方案时，需重点关注其自动化程度。任何需要人工干预的步骤（如手动确认故障、执行切换脚本）都会显著增加RTO。全自动化的故障检测与切换流程是实现低RTO的基石。

第三步：进行成本效益分析

更低的RTO/RPO意味着更高的技术复杂度和成本。您需要权衡"投入"与"风险"。

投入成本：包括硬件/软件采购、网络带宽（尤其是跨数据中心的同步复制对带宽质量和延迟要求极高）、运维人力成本等。
风险成本 ：即第一步中估算的业务中断损失 。其计算公式可参考为：总损失 = (中断时间 × 单位时间收入损失) + (数据丢失量 × 数据价值) + 商誉/合规损失。
平衡点 ：容灾设计的目标不是追求"零中断"，而是找到业务的风险容忍度 与控制措施成本之间的最优平衡点。例如，一个每小时损失10万元的系统，投入200万元建设容灾是合理的；而一个每小时损失1000元的系统，则可能选择更经济的方案。

第四步：通过演练进行实测与验证

"纸上得来终觉浅"，所有理论评估都必须通过定期的容灾演练来验证。

演练指标监控：
- RTO达成率：实际恢复时间是否满足预设目标？
- RPO达成率：恢复后的数据是否与故障发生点一致？
- 业务恢复成功率：所有关键业务是否都成功恢复？
- 流程规范性：切换过程是否顺畅，有无意外情况？
持续优化：演练结果应直接用于优化容灾方案和应急预案。例如，阿里云通过混沌工程工具AHAS-Chaos主动注入故障，不断验证和打磨其多活容灾架构MSHA的可靠性。

总结

总而言之，量化评估容灾方案的影响是一个闭环过程：从业务需求出发，映射到技术方案，权衡其成本效益，并最终通过实战演练进行验证和持续优化。清晰的定义、科学的分析和持续的验证，是确保您的容灾方案真正能为业务连续性保驾护航的关键。

1.4 拓扑数据分析

1.4.1 持续同调

持续同调（Persistent Homology）是拓扑数据分析（TDA）中的核心工具，它通过一种称为"条形码 "的直观方式，来量化数据在不同尺度下的拓扑特征。当应用于道路网络时，这些条形码就像给网络做了一次"CT扫描"，能深刻揭示其结构的稳定性、冗余度以及脆弱环节。

下面这个表格可以帮助你快速理解不同类型的条形码及其在道路网络中的直观含义。

条形码类型	代表的拓扑特征	在道路网络中的直观比喻与稳定性含义
0维条形码	连通分支	将每个交叉口视为点，随着连通距离增大，孤立的区域会连接起来。长条码代表稳定的、联系紧密的社区或区域。
1维条形码	环状结构	代表网络中的"环路"。长条码表示稳定存在的大环（如城市环线），意味着冗余路径多，稳定性强。
高阶条形码	高维空洞	在更复杂的空间结构中存在，道路网络中较罕见，可能对应特殊的立体交通枢纽。

如何生成道路网络的条形码

理解条形码的含义后，我们来看看它是如何从具体的道路网络中产生的。这个过程就像用不同的"放大镜"来观察网络：

构建网络 ：首先，将道路网络抽象为一个图，其中交叉口作为节点 ，道路段作为边。
定义"尺度" ：选择一个尺度参数（通常用交叉口之间的距离或通行时间来表示）。
逐步"连接"：从尺度为0开始，此时每个交叉口都是孤立的点。然后逐渐增大尺度参数，当两个交叉口间的距离小于等于当前尺度时，就在它们之间连上一条边。
追踪特征变化：在这个尺度由小变大的过程中，拓扑特征（连通区域、环路）会随之"出生"和"死亡"。例如，一个连通区域的"出生"是尺度增大到足以连接其中某些点时，"死亡"则是其与另一个区域合并时。一个环路的"出生"是形成封闭圈时，"死亡"则是圈内区域被完全填满时。
记录为条形码：为每个观测到的拓扑特征在数轴（尺度参数）上画一条线段，起点是其"出生"的尺度，终点是其"死亡"的尺度。所有特征的线段集合就构成了条形码。

通过分析这些条形码，我们可以超越传统的图论指标，从"形状"的角度深刻理解道路网络的本质特性。

量化评估稳定性的关键指标

要从条形码中提取具体的稳定性数值，通常关注以下几个核心指标：

评估目标	关键指标	指标解读
整体鲁棒性	持久性寿命均值/方差	计算所有条码（或某维条码）的"死亡时间-出生时间"的统计值。均值越大，表示网络整体拓扑特征越稳定；方差越小，说明网络结构越均匀。
特征重要性	单个条码的持久性	重点关注那些"寿命"极长的条码。例如，一个从很小尺度产生直到尺度极大才"死亡"的1维条码，可能对应着城市的核心环线，是网络稳定性的关键支柱。
结构复杂性	各维贝蒂数条形码数量	在特定尺度下，存活的条码数量即为该维的贝蒂数。通过观察不同尺度下贝蒂数的变化，可以了解网络结构的层次性。

实际应用与价值

在实际的城市路网分析中，这种方法能提供独特的洞察：

识别关键基础设施 ：通过寻找那些"寿命"最长的1维条码，可以精准定位对网络连通性至关重要的环线或主干道。这些道路是网络的"骨架"，它们的拥堵或损坏会对全局稳定性造成巨大冲击。
评估不同区域的结构稳定性 ：可以对城市不同区域（如老城区与新建开发区）的路网分别进行持续同调分析。通过比较其条形码特征，可以量化评估哪个区域的路网结构更鲁棒，这对城市规划有重要指导意义。
模拟故障影响 ：通过模拟移除某些路段或交叉口（这在拓扑上相当于改变过滤规则），然后重新计算条形码，通过对比"手术"前后拓扑特征的稳定性变化，可以定量评估局部故障对全局结构的影响，识别出潜在的脆弱点。

总结

总而言之，持续同调中的条形码提供了一种强大且直观的数学工具，它将道路网络的几何连接信息，转化为关于其深层结构稳定性的拓扑洞察。通过分析条码的"长短"和"分布"，我们能够超越传统的网络指标，从"形状"的维度评估网络的冗余性、鲁棒性，并识别出对稳定性至关重要的核心结构和潜在的脆弱环节。

1.5 智算中心DDC（Distributed Disaggregated Chassis）架构

1.5.1 DDC架构数学基础、业务场景映射以及性能界限

DDC（Distributed Disaggregated Chassis）架构通过其独特的网络拓扑和资源调度方式，在现代智算中心承载着关键任务。理解其背后的图论、复形几何原理及网络流特性，对于优化各类业务场景（如All-reduce）的性能至关重要。数学基础、业务场景映射以及性能界限三个层面，系统解析DDC架构的核心原理与约束。

数学基础与分析方法

DDC架构的核心数学思想是将物理资源（CPU、GPU、交换机、链路）及其连接关系抽象为复杂的网络模型，以便用严谨的数学工具进行分析和优化。

图论与复形几何抽象

DDC网络本质上是一个有向图 G=(V,E)，其中顶点集 V代表各种计算和交换设备，边集 E代表它们之间的物理或逻辑连接。基于此基础抽象，更高级的模型得以构建：
- 对偶图视角 ：在分析网络流路径时，我们常使用对偶图 。在对偶图中，原图的边（物理链路）变为顶点，原图中路径的连续性变为对偶图中的边。这种视角转换有助于优化全局路由策略，特别是在为All-to-All这种通信模式寻找最优多路径时非常有效。
- 单纯复形建模 ：为了描述设备间超越成对连接的高阶相互作用 （例如，多个GPU协同执行一个计算任务），可以引入单纯复形。一个k维单纯形由k+1个顶点及其所有子集构成，这非常适合对计算任务、数据流和故障域之间的群体依赖关系进行建模。其链复形 和 同调群 可用于分析网络的连通性，同调群中的非平凡元素可能指示着网络中存在潜在的通信瓶颈或冗余路径。
网络流算法与关键指标

网络流算法旨在优化数据在DDC这个图上的传输。
- 局部性与路径多样性 ：局部性旨在将通信频繁的节点（如通过NVLink直连的GPU）在拓扑上放置得更近，以减少跳数。这常通过图划分算法 （如Metis）将图划分为多个模块（类似DDC中的节点组），并最大化模块内连接，最小化模块间连接。路径多样性则通过多商品流问题 建模，目标是在满足所有流量需求的同时，最小化最大链路利用率或总延迟。DDC中采用的信元喷洒技术 ，可视为将大数据流分解为微小的、不可再分的信元，从而在对偶图 上运用最大流算法（如Dinic算法）来动态寻找可用路径，有效避免拥塞。
- 延迟建模：端到端延迟 De2e可初步估算为 De2e=Dprop+Dtrans+Dqueue，其中 Dprop是传播延迟（与物理距离和跳数正相关），Dtrans是传输延迟（与数据包大小和带宽负相关），Dqueue是排队延迟（与网络拥塞程度相关）。DDC的目标是通过拓扑和流控机制，有效降低这三项，尤其是 Dqueue。

业务场景的数学映射与优化

不同的集体通信模式（Collective Communication Pattern）对DDC网络提出了不同的挑战，其优化策略也深深根植于上述数学原理。

不同业务场景下的核心挑战与DDC的数学优化思路。

业务场景	核心挑战	图论/复形几何分析	网络流与局部性优化策略
All-Reduce (Scatter + AllGather)	避免全局同步点成为瓶颈；最小化树形通信的深度。	建模为在生成树（如最小生成树MST）或最优广播树上的操作。复形几何用于分析多个节点组（Simplex）在归约过程中的协同。	利用图划分将节点分为多个局部组，先在组内进行局部归约（优化局部子图），再进行全局归约。路径多样性用于构建多棵并行广播树。
All-to-All	绝对的带宽密集型，要求所有节点对之间都有高效路径。	对偶图视角至关重要，需要检查图的边连通度是否足够高。可视为在超立方体等拓扑上寻找节点不相交路径的问题。	DDC的信元喷洒本质上是将单流拆分为多流，在对偶图上实现等效多路径（ECMP）的极致利用，避免热点。
Scatter / Gather	根节点的出口带宽和连接数可能成为瓶颈。	分析图的出度和最短路径树。目标是最小化树的高度和最大节点度。	采用多根节点或构建更优的散射树（如双树散射算法），分散根节点压力。

故障容错性与快速恢复 ：DDC的高可用性依赖于其快速故障检测与路径切换能力。这可以通过图论中的连通性 概念来形式化。例如，若网络拓扑是k-点连通 或k-边连通 的，则意味着至少需要k个点（或边）发生故障才会使网络不连通。基于此，可以设计算法，在检测到边 e失效后，在多项式时间 O(∣E∣+∣V∣log∣V∣)内计算出一条避开故障边的最短路径。更为先进的策略是利用预计算的不相交路径 。例如，为关键流量计算多条边不相交 或节点不相交 的路径（可用Suurballe算法 求解）。一旦主路径故障，可瞬时切换至备用路径。从复形几何的视角看，一个健壮的DDC网络 ，其对应拓扑的一阶同调群应当是平凡的（即没有"洞"），这意味着任何局部故障都能被快速绕开，数据流仍能找到通路。

性能的界限与约束因素

任何设计都有其理论极限和实际约束，DDC架构也不例外。

理论上界（Upper Bounds）
- Bisection带宽 ：这是衡量网络容量的关键指标，指将网络分成两个相等部分所需切割的最小链路容量之和。它决定了All-to-All通信的最大聚合带宽。
- 图的直径 ：图中任意两点间最短路径的最大值。它决定了理论最小延迟的下界，因为数据包至少需要经过"直径"数量的跳数。
- 扩展性限制：随着节点数 N的增加，若要保持常数度的拓扑（如超立方体，度数为 logN），其直径也会以 logN增长。而若想保持小直径（如Dragonfly拓扑），则节点度数可能需要随 N增长，对交换机端口数提出挑战。
实际约束与下界（Lower Bounds & Practical Constraints）
- 交换机端口数 ：这是最硬的物理约束，直接限制了每个交换机能够连接的设备数量，从而影响拓扑结构的选择和局部子图的规模。
- 链路带宽 ：物理链路的带宽上限构成了单条路径的吞吐量上限。
- 控制平面开销 ：维护全局网络状态（如SDN控制器）、执行分布式路由算法都会引入开销。当网络规模极大、流量模式极度动态时，这些开销可能成为瓶颈，使得理论上的最优流难以在现实中实现。
- 故障恢复时间下界 ：故障检测（如通过BFD协议）和收敛需要时间，这决定了**服务恢复时间（RTO）** 存在一个不可逾越的下界。

总结

总而言之，DDC架构的性能和可靠性深植于图论、复形几何和网络流算法的数学基础之上。

1.5.2 DDC架构中，路径多样性与延迟之间的权衡

在DDC架构中，路径多样性与延迟之间的权衡是一个核心的优化问题。这种关系可以通过一个结合了网络流理论 和排队论的数学模型来定量描述。

为了直观地展示这种权衡关系以及关键参数的数学表达，请先看下表：

符号	含义	与DDC架构的关联
K	源节点与目标节点间并行的可用路径数量	代表了路径多样性。DDC中通过多轨道或端口绑定实现。
λ	数据流的总到达率（单位：数据包/秒）	表示需要传输的总负载。
λi	第 i条路径上分配的数据流到达率	λ=∑i=1Kλi，即总负载被分配到各路径。
μi	第 i条路径的服务率（由链路带宽、传播延迟等决定）	表示单条路径的理论最大处理能力。
ρi=μiλi	第 i条路径的利用率	必须满足 ρi<1，否则队列将无限增长，延迟趋于无穷。
Di	数据包在第 i条路径上的平均端到端延迟	是路径多样性与延迟权衡的最终体现。

延迟的定量模型

基于上表参数，单条路径上的平均延迟 Di可以建模为几个关键延迟分量的和：

复制代码

Di=Dprop,i+Dtrans,i+Dqueue,i

其中：

Dprop,i是传播延迟，由物理距离和光速决定，对于一个固定的网络拓扑是常量。
Dtrans,i是传输延迟，与数据包大小 L和路径带宽 Bi相关（Dtrans,i=L/Bi）。
Dqueue,i是排队延迟，这是受路径负载影响最大的变量。在M/M/1排队模型下，其期望值为 Dqueue,i=μi(1−ρi)ρi。

因此，单路径总延迟为：

复制代码

Di=Dprop,i+BiL+μi(1−ρi)ρi

而整个连接的总体验延迟 Dtotal，可以近似为各路径延迟的加权平均（按负载分配比例）：

复制代码

Dtotal≈i=1∑K(λλi⋅Di)

权衡关系的数学表达

路径多样性 K如何影响总延迟 Dtotal？关键在于负载分配。

低路径多样性（K小）的风险 ：如果可用路径少，总流量 λ必然集中在少数路径上，导致这些路径的 λi很大，利用率 ρi很高。根据排队延迟公式，当 ρi→1时，Dqueue,i→∞，从而显著增大 Dtotal。这就是拥塞导致的延迟爆炸。
高路径多样性（K大）的收益与成本 ：增加 K意味着可以将总流量 λ分散到更多路径上，从而降低每条路径上的负载 λi和利用率 ρi。这能有效降低排队延迟 Dqueue,i。

然而，这并非没有代价：
1. 控制开销：管理和协调 K条路径需要额外的控制信息交换。这部分开销可建模为总流量的一個函数，例如 C(K)=c⋅K⋅λ，其中 c是一个很小的系数。这会导致有效吞吐的轻微下降。
2. 路径差异：不同的路径可能具有不同的固有属性（如 Dprop,i和 Bi）。如果某些路径的固有延迟很高，将流量引入这些路径反而会增加平均延迟。

优化模型与设计不等式

因此，DDC架构中的路径选择问题，可以转化为在给定总流量 λ和网络路径集的情况下，寻找一个最优的流量分配方案 {λ1,λ2,...,λK}，以最小化总延迟 Dtotal。这通常表述为一个凸优化问题：

复制代码

minimizeDtotal=i=1∑K(λλi⋅Di(λi))

复制代码

subject toi=1∑Kλi=λ,and0≤λi<μi∀i

在实际工程中，一个关键目标是避免网络进入排队延迟主导的非线性增长区 。这引出了一个重要的设计不等式：

复制代码

ρi=μiλi≤ρthreshold

通常设定 ρthreshold∈[0.5,0.8]。这个不等式意味着，要控制高延迟，就需要确保有足够多的路径 K，使得每条路径上的负载 λi满足：

复制代码

λi≤ρthreshold⋅μi

因此，所需的最小路径数 Kmin应满足：

复制代码

K≥Kmin=⌈ρthreshold⋅μavgλ⌉

其中 μavg是平均路径服务率。这个公式定量地描述了为满足特定延迟目标（隐含在 ρthreshold的选择中），所需的最低路径多样性。

总结

总而言之，DDC架构中路径多样性与延迟的定量关系，可以清晰地通过基于网络流和排队论的数学模型来描述。增加路径多样性（K↑）通过分流负载来降低排队延迟，但可能引入额外的控制开销和次优路径风险。 工程上的最佳点，就是通过优化流量分配，在满足 Dtotal≤SLA（服务等级协议）约束 的前提下，找到使排队延迟和控制开销之和最小的那个 K值。

1.5.3 用凸优化方法求解最优流量分配问题

在DDC架构中，使用凸优化方法求解最优流量分配问题，核心思想是将物理网络的复杂约束和目标转化为一个可以高效求解的数学模型。其目标通常是在满足链路容量和流量守恒等硬约束的前提下，优化网络的整体性能，例如最小化最大链路利用率或总延迟。

模型基础：符号定义

首先，我们明确模型中的变量和集合：

图模型：将DDC网络抽象为一个有向图 G=(V,E)。其中，V是节点（NCP和NCF）的集合，E是链路（如NCP与NCF之间的SFI接口）的集合。
流量需求：设有一组需要传输的数据流 F。对于某条流 f∈F，sf表示其源节点，tf表示其目标节点，df表示其流量需求（速率）。
决策变量：xfe表示数据流 f在链路 e上分配的流量。这是我们需要优化的变量。
链路容量：ce表示链路 e的物理带宽容量。

凸优化问题建模

接下来，我们建立凸优化问题，其标准形式包含一个目标函数和若干约束条件。

目标函数

一个常见且实用的目标是最小化最大链路利用率。这能有效防止网络中出现局部瓶颈，实现负载均衡，与DDC通过信元喷洒实现高效负载均衡的设计目标高度一致。

复制代码

Minimizeα

复制代码

Subject to:f∈F∑xfe≤α⋅ce,∀e∈E

其中，α是一个辅助变量，代表所有链路中的最大利用率。最小化 α就是迫使流量尽可能均匀地分布在各条链路上。

约束条件

链路容量约束：任何链路上的总流量不得超过其物理容量。这在目标函数的约束中已体现：∑f∈Fxfe≤ce(当 α≤1时)。
流量守恒约束：对于每个流 f和每个网络中的中间节点 v（即既非源点 sf也非汇点 tf的节点），流入的流量必须等于流出的流量。这保证了数据不会在中间节点无故消失或产生。
复制代码
```
e∈δ−(v)∑xfe−e∈δ+(v)∑xfe=0,∀f∈F,∀v∈V∖{sf,tf}
```
其中，δ−(v)和 δ+(v)分别表示指向节点 v和从节点 v指出的链路集合。
需求满足约束：对于每个流 f，从源点 sf流出的净流量应等于其流量需求 df，而流入汇点 tf的净流量也应等于 df。
复制代码
```
e∈δ+(sf)∑xfe−e∈δ−(sf)∑xfe=df,∀f∈F
```
复制代码
```
e∈δ−(tf)∑xfe−e∈δ+(tf)∑xfe=df,∀f∈F
```
非负约束：链路上的流量不能为负。
复制代码
```
xfe≥0,∀f∈F,∀e∈E
```

模型与DDC架构的深度融合

上述模型是一个基础框架。要精准刻画DDC的特性，还需引入来自其核心机制的特定约束：

VOQ信用机制约束 ：DDC采用VOQ技术，发送端NCP在转发数据前需要先接收来自接收端NCF的信用，以确保对方有足够缓存。这可以建模为对每条链路 e上瞬时流量 xfe的短期突发约束。例如，可以添加约束限制在特定时间窗口 T内，链路 e上流入的流量总和不超过接收端缓存大小 Be：
复制代码
```
∫tt+Tf∈F∑xfe(τ)dτ≤Be,∀e∈E,∀t
```
在离散时间的优化模型中，这可以简化为对 xfe的额外上限约束。
信元喷洒的负载均衡 ：DDC将数据包切片为信元，并通过轮询机制喷洒到所有可用路径上。这意味着对于同一个数据流 f，其在多条等价路径 上的分配应尽可能均匀。这可以引导我们在求解上述优化问题后，制定相应的流表规则，使最终流量分布接近理论最优解 xfe∗，从而实现类似信元喷洒的效果。

求解与部署

问题性质 ：这个优化模型（以最小化最大链路利用率为例）是一个线性规划问题，它是凸优化的一种特例，存在非常成熟的高效求解算法（如内点法）。
求解器：可以使用专业的数学规划求解器（如Gurobi, CPLEX）或专门的网络流算法库进行求解。
部署流程：
- 集中式优化：由一个中央控制器（如SDN控制器或DDC架构中的NCC）收集全局网络状态（拓扑、容量、当前流量需求）。
- 求解问题：控制器运行优化算法，计算出最优的流量分配方案 {xfe∗}。
- 下发策略：控制器将计算出的路径和带宽分配策略转化为具体的流表规则，通过南向接口（如NetConf）下发到各个NCP设备上。
- NCP执行：NCP设备根据收到的策略，结合VOQ和信元交换机制，执行精确的流量调度与转发。

总结

通过上述凸优化模型，DDC架构可以从宏观上科学地指导流量分配，使其与底层VOQ、信元喷洒等转发机制紧密结合。最终在满足各种物理和协议约束的前提下，达成网络全局负载均衡、避免拥塞、提升吞吐量的目标，从而支撑AI训练等高负载业务对网络的高要求。

1.5.4 几种关键模型及其在 DDC 网络中的应用侧重点

在 DDC 这种复杂的网络架构中，传统的 M/M/1 模型确实显得过于理想化了。为了更精确地描述其延迟行为，我们需要一系列更贴近现实的排队论模型。几

模型类型	核心特征	为何更适合 DDC 网络	解决的 DDC 关键问题
M/M/c	多个并行的相同服务节点（服务器）	DDC 中计算、存储或转发资源常以资源池形式存在，并非单点服务。	精确计算当任务请求到达时，在多个可用服务单元前的排队等待时间。
M/D/c	服务时间是确定的，非随机，多个并行服务器	适用于处理时间近乎恒定的操作，如交换机在固定端口速率下的数据包转发。	更准确地刻画数据传输延迟中相对固定的部分，降低预测方差。
优先级排队	根据任务关键程度（如控制信令 vs 数据同步）划分服务等级	DDC 需要区分不同 SLA 的业务流量，确保高优先级任务的低延迟。	实现服务差异化，保证关键任务（如资源调度信令）不被普通数据流阻塞。
级联排队网络	将网络视为多个串联或更复杂连接的排队节点	DDC 中的数据包通常需要经过多个处理节点（如多个交换机或虚拟网络功能）。	准确分析数据包在整条路径上的端到端总延迟，而不仅仅是单点延迟。

M/M/c 模型：描述资源池的并行处理能力

当 DDC 架构中存在多个功能相同的服务节点（如一组执行相同任务的服务器或一个多端口交换机）时，M/M/c 模型比 M/M/1 更为精确。

核心思想 ：该系统有 c个并行且相同的服务台。任务到达后，如果存在空闲服务台，则立即被服务；如果所有服务台都忙，则任务进入一个公共队列等待。
DDC 应用场景 ：非常适合模拟一个多核服务器 处理到达的请求，或者一个多端口交换机处理来自多个上游设备的数据流。
优势：它能更准确地反映资源池的规模效应。随着 c（服务台数量）的增加，系统的整体服务能力增强，在相同负载下，任务的平均等待时间会显著低于 M/M/1 模型预测的结果。这对于 DDC 中水平扩展的资源池的性能评估至关重要。

M/D/c 模型：刻画恒定服务时间

在许多硬件处理环节，服务时间是高度确定而非随机的。例如，网络交换机在特定端口速率下转发一个固定长度的数据帧所需时间是常量。

核心思想 ：该模型假设服务时间是固定的（Deterministic, 故为 D），而非指数分布。结合 c个并行服务台，它描述了处理时间可预测的场景。
DDC 应用场景 ：精确模拟交换机端口的数据转发延迟 、某些专用硬件 （如智能网卡）的处理时间，或执行时间高度可预测的轻量级计算任务。
优势：由于服务时间无波动，M/D/c 模型预测的延迟方差远小于 M/M/c 模型。这有助于更准确地评估 DDC 网络数据传输的最坏情况延迟，对于保证确定性延迟需求的业务（如实时控制）非常关键。

优先级排队模型：实现服务等级差异化

DDC 网络需要同时承载对延迟敏感程度不同的多种业务流（如虚拟机迁移大数据流与实时健康检查信令）。简单的先到先服务（FCFS）规则无法满足需求。

核心思想 ：任务被划分为不同的优先级等级。高优先级任务到达时，可以中断正在服务的低优先级任务（强占式），或至少在其之后优先获得服务（非强占式）。
DDC 应用场景 ：用于实现服务质量 策略。例如，确保网络控制平面的信令（高优先级）永远比数据平面的普通流量（低优先级）优先处理，从而保证网络的稳定性和响应速度。
优势：该模型允许网络管理员为不同类型的流量提供差异化的延迟保证。这对于在共享的 DDC 基础设施上同时运行关键任务应用和普通业务至关重要。

级联排队网络：分析端到端路径延迟

在 DDC 中，一个任务或数据包通常需要经过一系列处理节点，例如：计算节点 -> 虚拟交换机 -> 物理交换机 -> ... -> 目标存储节点。其总延迟是路径上各节点延迟之和。

核心思想 ：将整个数据路径建模为多个排队系统的串联或更复杂的网络连接。数据包在每个节点都会经历排队和处理延迟。
DDC 应用场景 ：这是分析 DDC 端到端延迟 最准确的模型之一。通过将每个网络设备（交换机、路由器）和处理单元（服务器）抽象为一个排队节点，可以计算出一个数据包从源到目的地的总时间。
优势：它揭示了延迟的累积效应。即使每个节点的平均延迟都很低，但多个节点的延迟叠加，或者某个节点成为瓶颈，都可能导致显著的端到端延迟。这对于性能瓶颈定位和系统容量规划极其重要。

如何选择适合的模型

选择哪种模型取决于您的具体分析目标：

若要分析单个资源池 （如一组服务器）的吞吐量和延迟，M/M/c 是很好的起点。
若关心硬件转发 等具有确定服务时间的环节，M/D/c 能提供更精确的估计。
若需评估不同业务流的服务质量 和延迟保障，优先级排队模型是必然选择。
若要进行全局性能优化 和瓶颈分析，则必须采用级联排队网络来建模完整的数据路径。

1.5.5 DDC架构中的路径多样性

在DDC架构中，路径多样性（通常由参数 K 表征，可理解为等价并行路径的数量）的取值，确实会显著影响网络的可扩展性和总体成本。这个"K"可以被理解为构建网络"骨架"时核心的并行路径数量，它决定了网络的扩展潜力和经济性。

特性维度	小K值（路径少）	大K值（路径多）	核心影响机制
可扩展性	较低：网络规模易受限于初始设计，扩容可能需改变基础拓扑。	较高：提供丰富连接，支持通过增加设备"横向"平滑扩展至超大规划（如万卡集群）。	K值决定了网络"分支"能力。高K值架构（如多级POD）能像搭建积木一样扩展。
硬件成本	相对较低：所需互联端口和线缆较少，初始投入可能更低。	显著增高：每台NCP需上联到更多NCF，且NCF间需大量高速互联，导致端口数、线缆、功耗激增。	成本与K值非简单线性，可能呈指数增长。大K方案需评估"规模经济"能否摊薄单端口成本。
布线与管理复杂度	相对简单：物理布线和逻辑配置的复杂度可控。	极其复杂：设备间大量高速线缆互联，布线挑战大；集中控制面故障风险高，需分布式OS管理。	复杂度随K值增加而飙升，是制约K值上限的关键工程因素。
理论性能潜力	相对受限：易在核心路径出现瓶颈，All-to-All等通信模式效率较低。	极高：信元喷洒（Cell Spraying）等技术支持流量在K条路径上实现近乎理想的负载均衡，提供巨大聚合带宽。	高K值是实现无阻塞、高吞吐网络的基础，但需VOQ和信元交换等高级机制配合。

理解K值的含义

在DDC架构中，路径多样性（K）并不仅指物理链路的数量，它更核心地体现在网络逻辑层面的并行通道 上。DDC通过将传统框式交换机的交换网板和业务线卡解耦为独立的NCF 和NCP设备，再通过高速网络互联，形成了灵活的"盒盒"组网。路径多样性（K）在此背景下，深刻影响了网络的扩展性和成本。

寻找最优K值范围

关于"理论上的最优K值范围"，并不存在一个"放之四海而皆准"的精确数字 。最优K值是特定业务目标、技术可行性和经济成本之间权衡的结果。

业务需求是首要决定因素
- 当前与未来集群规模 ：这是决定K值的首要因素。若目标仅是支撑数百卡 的AI训练集群，一个中等K值的单POD设计可能已足够高效且经济。但如果规划是数千至数万卡的超大规模集群，则必须采用高K值的设计（如多级POD互联），否则网络将成为无法扩展的瓶颈。
- 通信模式：如果业务以All-to-All（如大规模分布式训练）、All-Reduce等通信模式为主，对网络吞吐和延迟极其敏感，那么更高的K值所带来的路径多样性和负载均衡能力几乎成为必选项。
技术水平的约束
- 运维能力：K值越高，网络拓扑和流量调度越复杂，对运维团队的技能要求也呈指数级增长。选择超出团队运维能力的K值，会导致网络稳定性灾难。
- 协议与设备成熟度：高K值架构依赖于VOQ（虚拟输出队列）、信元交换、分布式控制平面等技术的成熟度。这些技术的可靠性和性能，决定了实际K值能取到的上限。
成本效益的平衡点
- 最优K值是一个动态范围 ，而非固定值。它需要根据每单位有效带宽的成本（Cost per Usable Bandwidth） 来确定。目标是找到扩展性提升带来的收益（如训练时间缩短、GPU利用率提升）与硬件及运维成本增加之间的拐点。
- 业界一些设计（如新华三的方案）通过优化，在单POD内实现了9216个400G端口的规模，这本身就是对其特定技术条件下"较优K值"的一种工程实践。

总结与决策建议

总的来说，路径多样性K值的选取，本质是在网络性能与扩展性 和实现成本与复杂度 之间寻求最佳平衡。

明确业务规模 ：首先精准定义当前及未来3-5年所需支撑的最大计算集群规模 和主流通信模式。
设定性能目标 ：明确网络需要达到的吞吐量 和延迟目标，特别是要满足GPU利用率的要求。
评估约束条件 ：清晰评估预算上限 和团队的技术储备与运维能力。
参考最佳实践 ：研究现有成熟方案（如厂商提供的POD设计参考）。例如，一个旨在支撑万卡级别 集群的方案，其K值（反映在NCP上联NCF的数量、POD间互联的丰富程度）通常会显著高于一个仅为千卡级别设计的方案。

1.6 万卡级别的超大规模集群的扩展性方法

对于万卡级别的超大规模集群，要实现真正的可扩展性，确实不能仅仅依赖增加路径数量（K值）。这需要一个从网络拓扑、资源组织方式，到协议与控制平面，乃至散热供电等基础设施的系统性协同设计。

设计方向	核心目标	代表性架构或思路
网络拓扑创新	降低网络直径，避免瓶颈，实现成本与规模的亚线性增长	阿里HPN（双层CLOS）、华为UB-Mesh（分层局部多维全互联）
资源组织方式	将庞大集群划分为可管理、可独立扩展的故障域和资源池	模块化设计（POD/Block）、计算/存储/网络解耦
协议与控制平面	让网络从"静态管道"变为可智能调度、自愈的"动态系统"	端网协同（如TCCL/GOR）、集中式+分布式混合控制
基础设施与平台	保障集群在高功率密度下的稳定运行与高效运维	液冷散热、智能电控、自动化运维与健康监测

网络拓扑的创新

传统多层CLOS拓扑在规模极大时，成本和复杂度会急剧上升。业界正探索更扁平、更智能的拓扑。

更扁平的层次 ：阿里的HPN架构 致力于用两层网络 实现超万卡互联。通过双平面设计 （将网络逻辑划分为两个平面）和多轨道连接（使服务器内每张GPU都有专属的高速网络通道），不仅减少了交换机数量以降低成本，还显著降低了通信延迟和哈希冲突风险。
异构混合拓扑 ：华为的UB-Mesh 构想了一种混合结构，在不同层级采用不同连接策略。其核心优势在于，规模扩展时成本呈亚线性增长，即规模扩大百倍，成本远低于百倍，为实现更大规模集群提供了经济可行的路径。

资源组织与调度优化

将集群视为一个整体"黑盒"会带来运维和效率挑战，需要通过模块化和智能调度来优化。

模块化与分层治理 ：将整个万卡集群划分为多个POD 或Block 。每个模块包含一定数量的计算、存储和网络资源，可独立运行和故障隔离。集群规模扩展时，以模块为单位进行扩容，极大简化了管理和故障定位。同时，阿里等厂商采用计算、存储、网络解耦的设计，各资源池可独立扩展，提升了灵活性。
调度器感知网络拓扑 ：先进的调度系统（如Kubernetes的定制调度器）能够感知底层网络拓扑。在分配任务时，会优先将通信紧密的Pod调度到网络距离最近的节点上，从而减少跨核心交换机的流量，优化通信效率。

协议与控制的智能化

网络设备的硬件能力需要智能的软件和协议来驱动。

端网协同技术 ：这是提升大规模集群效率的关键。以阿里的TCCL/GOR组合为例：
- TCCL：是运行在服务器上的"通信大脑"，能感知整个集群的网络拓扑。在发起通信前，它会智能规划路径，优先选择同一交换机下的短路径通信，并避免流量冲突。
- GOR ：是集群的"网络总指挥"，实时监控全网流量。一旦检测到拥塞，能在毫秒级内计算出新路径，并通知TCCL切换流量，实现动态负载均衡。
拥塞控制的优化 ：为避免传统无损网络中PFC机制带来的"广播风暴"风险，业界趋势是采用更智能的端到端拥塞控制算法（如HPCC），在保持低延迟的同时避免网络死锁。

基础设施与运维保障

强大的算力离不开稳定、高效的基础设施支撑。

绿色节能技术 ：万卡集群功耗巨大，液冷技术 （特别是浸没式冷却）因其散热效率远高于风冷，已成为超大规模集群的标配。它能有效控制芯片温度，保障计算稳定性，并有助于降低数据中心的PUE，实现节能目标。
全面的可观测性与自动化 ：在万卡规模下，硬件故障是常态而非例外。构建覆盖GPU、网络、存储等各层的实时监控系统 至关重要。通过采集大量数据，系统能自动预测、诊断故障，并结合调度系统实现故障自动隔离、任务自动迁移，从而将硬件故障对训练任务的影响降至最低，保障集群有效算力。

端网协同技术（如腾讯星脉网络中的TCCL和GOR）是现代万卡级AI集群的核心技术，它通过端侧（服务器）和网侧（网络设备）的深度协作，智能地调度网络流量，从而极大提升了大规模AI训练的效率和稳定性。

组件	核心职能	部署位置	关键价值
TCCL	端侧执行引擎：感知拓扑，规划最优通信路径，智能分配流量。	GPU服务器端	将AI训练的通信需求与物理网络拓扑精准匹配，实现静态最优路径规划。
GOR	网侧调度大脑：监控全网状态，实时感知拥塞，动态调度流量。	集中式控制器	赋予网络全局视角和实时反应能力，实现动态的拥塞规避与故障自愈。

工作机制详解

TCCL和GOR的协同工作，可以比作一个由"智能导航系统"和"全局交通管制中心"配合的高效体系。

TCCL：端侧的智能导航系统

TCCL运行在每个GPU服务器上，在通信开始前就进行精细优化。

拓扑感知与路径规划 ：传统集合通信库对网络物理拓扑不敏感。TCCL则从GOR获取全局网络拓扑图，在规划All-Reduce等操作时，遵循轨道亲和性原则，优先让同一交换机下的GPU进行通信，最大化利用本地链路带宽，最小化需要经过核心交换机的跨子网流量。
异构网络协同 ：服务器内部GPU间通过高速NVLink互联，而服务器之间通过RoCE网络互联。TCCL能够感知这种异构性，通过动态滑动窗口机制，根据NVLink和RoCE的带宽差异，智能地将待传输的数据切片，并同时利用这两类网络通道进行传输，从而压榨整体带宽。
哈希正交与冲突避免 ：为避免多条大数据流被网络设备的ECMP哈希算法映射到同一条物理链路上造成拥塞，TCCL会主动为并行的数据流分配一组哈希正交源端口号。这确保这些流能被均匀地分散到所有可用的物理链路上，从源头避免哈希冲突。

GOR：网侧的全局交通管制中心

GOR作为一个集中式控制器，实时监控并调度整个网络。

实时监控与毫秒级感知：GOR通过Telemetry、sFlow等技术，以毫秒级精度实时采集全网每条链路的负载和ECN拥塞标记数量，从而快速发现拥塞点。
精准定位与智能决策 ：一旦检测到拥塞，GOR会迅速定位到导致问题的Top-N"大象流"。随后，它基于实时网络拓扑和流量信息，为这些流计算新的、拥塞更少的路径。在决策前，GOR会进行"沙盘推演"，模拟流量切换后的效果，并递归验证新路径不会引发二次拥塞。
无损调度与路径切换 ：计算出新路径后，GOR通过控制通道通知源端服务器的TCCL。TCCL随即调整相应数据流的源端口号，引导流量无缝切换至新路径。整个过程对上层AI训练任务是无感且无损的，通常在一次训练迭代内完成。

性能提升数据

这套端网协同机制在实际部署中带来了显著的性能提升。

通信性能 ：在腾讯的大模型集群中，与NVIDIA的NCCL方案相比，星脉网络实现了25%的集合通信带宽提升 ，并将由流量冲突造成的网络拥塞问题减少了80%。
训练效率 ：对于All-Reduce这一关键通信操作，性能提升近20% 。对于更复杂的All-to-All通信，性能提升可达30%至50%。
故障恢复 ：GOR的动态调度能将网络拥塞的持续时间缩短超过90% ，告警恢复时间可控制在3分钟以内，显著提升了训练的稳定性和GPU的有效利用率。

总而言之，TCCL和GOR代表的端网协同技术，通过将网络的全局控制智能与服务器端的本地执行能力紧密结合，实现了从"被动承载"到"主动优化"的范式转变。它通过静态预规划 和动态重路由相结合，有效解决了万卡集群规模下的哈希冲突、拓扑盲点和拥塞抖动三大核心挑战，为大规模、长周期的AI训练任务提供了高效、稳定的网络底座。

通信模式的性能界限与数学约束

通信模式 / 业务场景	核心性能上界 (理论最优)	典型性能下界 (常见瓶颈)	关键约束与数学原理
All-Reduce (规约操作)	*O( (α + β M / P) * log P ) • α: 延迟，β: 带宽倒数，M: 数据量，P: 进程数。理想对数缩放**。	*O( (α + β M) * P ) • 网络直径大、路径多样性差时，退化为线性缩放**，性能急剧下降。	网络直径 (图论)、对分带宽。优化依赖通信调度树 (图) 的构造，避免链路冲突。
All-to-All (全交换)	*O( M P / B ) • B: 对分带宽。理想时均匀占用所有链路**。	*O( M P² / B ) • 拓扑盲点、哈希冲突导致流量局部聚集**，有效对分带宽骤降。	对分带宽 (图论)、ECMP哈希均匀性。需强正则图等高对称性拓扑避免热点。
Scatter / Gather (散射/聚集)	*O( α log P + β * M ) • 最优散射树深度**为对数阶。	*O( α P + β * M * P ) • 根节点成为单点瓶颈**，序列化操作导致线性延迟。	节点度、网络直径。利用多根节点或最优生成树 (图算法) 分散压力。

各类集合通信模式的性能上界，主要由网络拓扑这一"物理硬件"决定。

理论性能上界的基础
- 对分带宽 ：这是评估All-to-All类通信的黄金指标。它指将网络节点分为两个相等部分所需切割的最小链路容量之和 。一个网络的对分带宽直接决定了其All-to-All通信的最大聚合吞吐量。
- 网络直径 ：指网络中任意两点间最短路径的最大值 。它决定了单次点对点通信的理论最小延迟，是影响Scatter/Gather和All-Reduce等操作延迟下界的关键。
性能下界的成因：从理论到现实的差距

现实中的性能往往远离理论上界，核心原因在于流量竞争。例如，在非理想拓扑中，All-to-All通信可能因流量局部聚集导致有效对分带宽远低于理论值。同样，若All-Reduce的通信树构建不当（如深度过大或分支不均），其实际耗时将远高于O(log P)。

网络流优化：从静态规划到动态重路由

为逼近理论上界，需要一系列复杂的优化算法，其核心思想是感知状态，动态调整。

静态预规划与凸优化应用

在任务执行前，系统会进行静态规划。例如，TCCL 会从全局控制器GOR 获取全网拓扑信息，为All-Reduce任务构建一个拓扑感知的最优通信树 。这个过程可建模为一个凸优化问题（如最小化最大链路利用率）。
- 目标函数 ：例如，Minimize α（最大链路利用率）。
- 约束条件：包括流量守恒、链路容量限制等。通过求解该问题，可获得初始的最优流量分配方案 xfe∗。
动态重路由与协同控制

静态规划无法应对实时变化。因此，需要GOR这类控制器进行动态重路由。其核心机制可概括为：
- 感知：通过Telemetry、sFlow等技术，以毫秒级精度实时监控网络状态（如链路利用率、ECN标记）。
- 决策：一旦检测到拥塞，GOR会利用内置的ECMP哈希算法模拟器进行"沙盘推演"，递归验证新路径不会引发二次拥塞后，计算出最优的重路由路径。
- 执行：通过控制通道通知源端（如服务器的TCCL）修改流的源端口号，无感地将流量切换至新路径。
  
  这种机制将端到端的通信延迟降低了17.6%，并将平均排队分组数目减少了38.3%。

容错与快速恢复的数学本质

在万卡规模下，故障是常态。容错机制的核心数学本质是保持网络连通性。

故障检测、隔离与图论

故障检测可建模为网络连通性 的实时判断问题。系统持续监控，一旦发现节点或链路失效，即将其标记为"故障"，并在网络拓扑图 G中将其暂时移除。关键在于，剩余图的连通性 必须依然能满足业务需求，这依赖于初始拓扑设计时的高冗余度（如k-点/边连通）。
任务迁移与同调群

当故障导致一个计算节点失效，其上的任务需要迁移。从拓扑视角看，这相当于在单纯复形中移除一个单形（节点、边或面）。同调群 工具可以精确判断这一操作是否在网络中创造了"空洞"（即非平凡的拓扑障碍）。一个健壮的网络设计，应能保证在单个或少量组件故障后，其一阶同调群仍保持平凡，意味着数据流总能找到替代路径，从而保障任务的快速迁移和恢复。

统一的数学理论框架展望

（协同）对偶图视角

这是分析网络流问题的强大工具。在对偶图 中，原网络的边变为顶点，边的相邻关系变为新边。网络流问题在此视角下常可转化为更易解决的最短路径问题。例如，DDC架构中的信元喷洒机制，可理解为在对偶图上执行流分配。
同调群与连通性损伤分析

同调论 是代数拓扑中研究"空洞"的强大工具。在网络中，可用来量化故障模式对网络连通性的损伤程度。
- 0维同调群 ：其维度（Betti数 β₀ ）等于网络的连通分量个数。β₀ 增大意味着网络发生分裂。
- 1维同调群 ：其维度（Betti数 β₁ ）反映了网络中存在的"不可收缩的环"的数量，可用于量化冗余路径的丰富性。
  
  通过计算故障前后网络拓扑的同调群，可以精确定位网络的脆弱环节，并从拓扑层面进行加固。
概率图模型与不确定性推理

万卡集群的运行充满不确定性（负载波动、瞬时故障）。概率图模型 （如贝叶斯网络、马尔可夫随机场）非常适合对该系统进行建模。节点和链路状态可视为随机变量，其依赖关系用边表示。基于此模型，可以推理在部分观测信息下，网络全局状态的可能性，从而实现故障预测 和主动规避 。华为的数字化风洞 正是此类建模仿真思想的工程化体现，能够在部署前预演各种故障和负载场景，找到系统最优配置。

万卡/十万卡集群的通信优化，是一个在多层约束 下寻求全局最优的复杂系统工程。

性能目标 受限于由图论定义的网络拓扑基本属性（直径、对分带宽）。
优化方法 涵盖了从凸优化 （静态规划）到强化学习（动态决策）的算法谱系。
容错设计 则深深植根于代数拓扑 （同调论）和概率图模型，以确保系统的韧性。

在万卡乃至十万卡级别的超大规模AI集群中，确保训练任务的高效与稳定运行，确实需要一整套环环相扣的精密设计。这其中涉及了从底层网络拓扑、动态路由算法，到高层容错机制的复杂协同。

核心挑战领域	关键问题描述	核心解决方案与技术
拓扑设计与流量优化	如何降低延迟、避免瓶颈，并应对ECMP哈希冲突导致的流量不均？	分层CLOS拓扑、双平面设计、多轨连接、定制拥塞控制算法
动态路由与重路由	如何实时感知网络状态，动态规避拥塞，实现流量全局最优？	集中式控制器（如GOR）动态路径计算、端网协同（如TCCL感知拓扑）、基于实时遥测（Telemetry）的快速重路由
故障诊断与自愈	在万卡规模下，软硬件故障常态化的背景下，如何实现分钟级甚至秒级的故障发现、定位、隔离与恢复？	多层次监控与心跳机制、轻量级诊断测试、基于图论的故障域隔离、两阶段检查点技术

拓扑设计与流量优化

网络拓扑是集群的"骨架"，其设计直接决定了理论上的性能上限和可扩展性。

分层CLOS拓扑 ：诸如字节MegaScale等系统普遍采用类似CLOS的多层（如Spine-Leaf）交换架构 。这种架构的核心优势在于无阻塞转发 和多路径。任意两个节点之间存在多条等价路径，为实现负载均衡和冗余容错打下了坚实基础。
应对哈希冲突 ：传统的ECMP（等价多路径路由）在遇到大量并行的、特征相似的流量时（如All-Reduce通信），容易发生哈希冲突，导致链路负载不均。解决方案包括：
- 精细化的拓扑设计 ：如阿里HPN架构采用双平面设计，将一个大Pod划分为两个逻辑平面，从物理上隔离流量，极大降低了流量在核心层冲突的概率。
- 硬件层级优化：将一个大端口（如400G）拆分为多个小端口（如2个200G），以增加路径多样性。
智能拥塞控制：为避免全网拥塞，系统会采用结合了Swift和DCQCN原理的定制拥塞控制算法。这些算法能够更精确地测量网络状态并快速响应，从而显著提升吞吐量。

动态规划与重路由机制

静态规划再好，也无法应对动态变化。因此，需要一套"智能"的系统实时调度流量。

集中式控制与端网协同 ：理想的模式是"集中决策，分布式执行"。一个集中式控制器 （概念上类似华为的GOR）实时收集全网链路状态。部署在服务器端的智能通信库 （概念上类似TCCL）会从控制器获取全局拓扑视图，从而在发起通信时，能够依据实时网络状态进行静态预规划，例如优先选择同一交换机下的路径，减少跨核心交换机的跳跃。
动态重路由 ：当控制器通过Telemetry等技术检测到拥塞或故障时，会立即计算新的最优路径，并通知相关端点调整流量路径（例如通过更新源端口号来改变ECMP哈希结果)。这种 **"感知-决策-执行"** 的闭环，实现了网络流量的动态优化和故障的快速规避。

稳定性保障与故障自愈

在万卡规模下，"故障是常态，而非异常"。系统的韧性至关重要。

快速故障检测与诊断：
- 全栈监控：建立毫秒级精度的监控系统，从网卡端口、交换机队列到GPU进程的心跳，实现全方位覆盖。
- 精准诊断 ：一旦检测到异常（如心跳超时），系统会触发一系列轻量级诊断测试（如主机内网络环回测试、节点间NCCL All-Reduce测试），快速定位是网卡、线缆还是GPU的问题。
故障隔离与任务迁移：
- 基于图论的隔离 ：系统将集群资源抽象为图模型。当某个节点（Vertex）或链路（Edge）故障时，管理系统能快速识别其影响的子图（如一个机架内的所有GPU），并通过图操作 将其从资源池中"剔除"。阿里HPN架构中，通过单个GPU的网卡（NIC）双端口连接到不同的ToR交换机，提供了物理层面的冗余路径，本身就是一种基于局部连通图的高明设计。
- 快速检查点与恢复 ：采用两阶段检查点技术。训练状态先被快速写入本地NVMe存储，再由后台进程异步上传至分布式文件系统。恢复时，通过优化策略（如让同一数据并行组内的一个进程读取检查点并广播），避免所有进程同时访问存储瓶颈，从而将万卡集群的恢复时间从数小时缩短至分钟级。

在万卡乃至十万卡级别的超大规模AI集群中，为了实现极高的效率与稳定性，需要一套深度融合了排队理论、网络拓扑、数学优化和代数拓扑的精密系统。下面这个表格梳理了其核心机制与理论体系，希望能帮助您快速建立整体认知。

核心维度	关键挑战	核心技术方法	理论基础与目标
业务流服务质量与调度	多租户、多类型任务（训练/推理）对资源的需求和优先级不同，需避免低优先级任务阻塞关键任务。	优先级排队模型（如Slurm的多因子优先级计算）、抢占式调度、Gang Scheduling（All-or-Nothing）。	基于排队论，目标是最小化关键任务排队等待时间，保障SLA，最大化集群有效产出。
网络路径与性能	单一路径易成瓶颈，网络延迟会随路径跳数和拥塞而累积叠加，影响All-Reduce等集合操作效率。	路径多样性（ECMP, 多轨道设计）、拓扑优化（Clos/Fat-Tree）、端网协同（如TCCL/GOR）。	图论、网络流理论。目标是提供高对分带宽、低直径网络，实现负载均衡，避免局部瓶颈。
流量分配与优化	"信元喷洒"等负载均衡机制在路径不对称或拥塞时可能失效，导致哈希冲突和尾延迟。	凸优化进行离线流量规划，数值分析进行在线实时路由调整。	将流量分配建模为凸优化问题，在链路容量等约束下最小化最大链路利用率或总延迟。
网络健壮性分析	组件故障（链路、节点、交换机）常态发生，需量化其对网络连通性的损伤并快速恢复。	同调群分析连通性损伤，故障域隔离，快速重路由。	代数拓扑。通过计算故障前后拓扑的Betti数变化，量化网络"空洞"的生成，评估容错能力。
集合通信性能界限	不同通信模式（All-Reduce, All-to-All）在给定网络拓扑下存在理论上的性能上限和下限。	性能建模，理论证明（基于直径、对分带宽等图论不变量）。	建立理论证明体系，明确性能与拓扑的关系，为架构设计和优化提供理论依据和评估基准。

优先级排队与服务质量保障

在万卡集群中，任务队列管理是保证资源分配公平性和效率的核心。其目标是在多租户环境下，确保高优先级的紧急任务（如在线推理服务）能够优先获得资源，同时避免大型训练任务因长时间排队而"饿死"。

多因子优先级模型 ：如Slurm调度器采用复杂的公式动态计算任务优先级，综合考虑作业等待时间 、用户或项目的资源配额使用情况 、作业规模 以及指定的服务质量等级等多个因素。这使得调度决策不再是简单的先到先得，而是更智能地满足多样化的业务目标。
Gang Scheduling与抢占机制 ：对于大规模分布式训练任务，需要同时启动数百个GPU副本。Gang Scheduling 策略确保所有资源都到位后才启动任务，防止部分任务启动造成的资源死锁和浪费。同时，结合抢占机制，高优先级任务可以抢占低优先级任务占用的资源，并由平台负责为被抢占的任务创建检查点，以便后续无缝恢复，从而显著提升关键任务的交付速度。

路径多样性与延迟优化

网络是超大规模集群的神经系统，其设计的核心是为海量的东西向流量提供充足、高速且可靠的连接。

非阻塞拓扑与多路径 ：现代万卡集群普遍采用 Clos或Fat-Tree 等非阻塞网络拓扑 ，从而在任意两个节点间提供大量等价多路径 。结合端网协同技术，智能网卡和通信库可以感知网络实时状态，动态选择最优路径，有效规避拥塞点。
延迟累积与控制 ：一次分布式训练迭代的延迟取决于最慢的GPU。因此，不仅要降低单跳延迟，更要通过拓扑感知调度 （将通信频繁的Pod调度到同一机架或交换机下）来减少通信跳数，从而控制路径延迟的叠加效应。研究表明，优化的调度策略可带来超过20%的性能收益。

流量分配与数学优化

"信元喷洒"等动态负载均衡技术虽然能有效利用多路径，但在网络状态不均时可能导致流量不均衡。这就需要更精细的数学工具进行指导和优化。

凸优化模型 ：流量分配问题可被建模为一个凸优化问题，例如以最小化最大链路利用率为目标，以流量守恒和链路容量为约束条件。求解该模型可获得全局最优的流量分配策略，从理论上避免局部瓶颈。
数值分析与在线调整 ：凸优化通常用于离线规划。在线运行时，则需采用基于实时网络遥测的数值分析方法，持续监测链路利用率、丢包率、延迟等指标，并运用控制算法动态调整流表，实现自适应的流量工程。

同调群与网络健壮性

在万卡规模下，硬件故障是常态。代数拓扑中的工具为量化评估和增强网络的容错能力提供了强大视角。

同调群分析 ：可以将网络抽象为一个单纯复形 。同调群 ，特别是一维同调群 ，能揭示网络中的"环状"结构。其Betti数直观反映了网络中存在多少独立的、未被填充的"环"。当链路或节点发生故障时，可以通过计算同调群的变化来量化网络连通性的损伤程度。一个健壮的网络设计，应能保证在发生一定数量的故障后，其同调群结构保持稳定，即网络仍能保持良好连通。
故障模拟与韧性评估 ：通过模拟不同类型的故障模式（如单链路中断、整机柜故障），并观察同调群的变化，可以识别出网络中的关键脆弱点，从而有针对性地加强这些区域的冗余性。

集合通信的性能界限

各类集合通信操作的性能并非无限，其在特定集群架构下存在理论上的上限和下限。

性能上界 ：通常由网络的对分带宽 和直径等拓扑属性决定。例如，All-Reduce 操作的理论最优时间受限于数据量大小、网络延迟以及对分带宽。
性能下界与证明体系 ：通过图论和复杂性理论 可以建立不同通信模式在特定网络模型下的性能下界。这构成了一个理论证明体系，用于判断某个调度算法或通信库的实现是否已经接近理论最优，从而指导优化方向。

万卡/十万卡集群的高效稳定运行，是排队论、图论、凸优化和代数拓扑等多个数学工具在工程上深度融合的结果。优先级排队模型 和调度策略 保障了任务级别的服务质量；路径多样性 和流量优化 确保了网络数据通路的高效与可靠；而同调群等高级数学工具则从拓扑层面深刻揭示了系统的内在健壮性，并为容灾设计提供了理论依据。

优先级排队模型中的多因子权重动态调整，确实是一个直接影响系统效率和公平性的核心问题。

多因子权重动态调整的核心数学模型

动态权重的核心思想是：权重不应是固定值，而应成为连接系统状态与调度目标的"调节器"。一个经典且实用的动态权重模型可以表示为如下公式，它综合考虑了业务属性、实时状态和系统负载：

综合优先级分数 P = α(Load) × F₁ + β(Load) × F₂ + γ(Load) × F₃ + ...

其中，F₁, F₂, F₃ 代表不同的业务维度因子（如任务紧迫度、用户等级、资源需求等），而 α, β, γ 就是与系统实时负载 Load相关的动态权重。

任务紧迫度因子 (F₁) ：通常与任务的截止期限 负相关。例如，F₁ = 1 / (1 + max(0, 剩余时间 - 当前时间))。距离截止时间越近，该因子值越大，任务越紧迫。
用户/业务等级因子 (F₂)：这是一个由业务策略决定的静态值。例如，VIP用户发起的任务或核心业务对应的任务，该因子值更高。
资源需求因子 (F₃) ：通常与任务所需的资源量（如CPU、内存、GPU）正相关。关键在于，系统可以根据总体负载情况，动态改变这些因子的权重。
- 当系统负载较高时（如 >80%） ：应提升资源利用率因子的权重，鼓励系统接纳那些计算量大但能显著提升整体资源利用率的任务，避免资源闲置。同时，可适当降低对绝对延迟敏感的任务的权重，因为高负载下延迟难免会增加。
- 当系统负载较低时（如 <30%） ：应提升响应速度/任务紧迫度的权重。此时资源充裕，调度目标可以转向尽可能快地完成任务，优化用户体验。

下面这个表格展示了不同业务场景下的动态调整策略。

业务场景	核心目标	权重调整策略（示例）	预期效果
电商峰值（如双11）	保证交易链路稳定，最大化吞吐量	提升"业务关键性"和"系统吞吐量"权重，降低"资源消耗"权重。即使资源需求大，但支付、订单等核心任务也必须优先。	核心业务不中断，系统整体吞吐量最大。
AI训练集群	提高GPU利用率，保证大型作业完成时间	动态平衡"任务剩余耗时"和"资源利用率"。负载高时，优先运行能快速释放大量GPU的计算任务；负载低时，则优先运行大规模训练任务以避免资源碎片化。	提高GPU平均利用率，保障关键实验进度。
实时数据处理（如风控）	稳定且极低的处理延迟	显著提升"任务延迟"权重，并采用强占式调度。一旦有新的风控分析任务到达，可中断低优先级的批处理任务。	满足风控等实时业务的低延迟要求。
在离线混合部署	离线任务充分利用资源，但不影响在线服务	根据日峰谷动态调节。日间在线服务流量大，提升在线任务权重；夜间流量低，则提升离线计算任务的权重，充分利用资源。	实现资源分时复用，大幅降低成本。

动态调优实战案例

1. 基于负载预测的GPU资源调度

某AI计算平台为了应对工作日白天研究模型调试（短任务、高优先级）和夜间大规模模型训练（长任务、资源消耗大）的混合负载，设计了如下动态权重策略：

日间高负载期：权重偏向"任务延迟"和"用户等级"。教授或高工的交互式调试任务能获得快速响应，保证研究效率。
夜间低负载期：权重偏向"资源利用率"和"任务规模"。调度器会优先启动需要占用大量GPU的大型训练作业，从而提升整个集群的夜间资源利用率。

其权重更新算法可简化为：

复制代码

如果 平均负载 > 预设阈值：
    α = α * 1.1  # 提升资源利用率权重
    β = β * 0.9  # 适当降低其他权重
否则：
    α = α * 0.9
    β = β * 1.1

*（α, β 代表不同因子的权重）*通过这种方式，该平台在夜间低负载时段的有效计算利用率提升了近20%.

同调群分析为量化网络连通性损伤提供了强大的数学工具。它通过计算网络拓扑中的"空洞"数量（Betti数）来精确反映故障导致的连通性变化。下面我结合一个数学示例来说明其计算过程。

理解同调群与连通性的关联

首先，我们需要理解不同维数的同调群所揭示的网络结构信息：

0维同调群 ：其维度（0维Betti数 β₀ ）直接等于网络的连通分量个数。β₀ 增大，意味着网络发生了分裂。
1维同调群 ：其维度（1维Betti数 β₁ ）反映了网络中存在的"不可收缩的环"的数量。β₁ 可以直观地理解为冗余路径的丰富性。一个环意味着存在一条替代路径，即使某条边失效，信息仍可流通。

因此，通过计算故障前后网络拓扑的 Betti 数变化，可以精确定量连通性的损伤程度。

数学计算示例：一个简单网络的故障分析

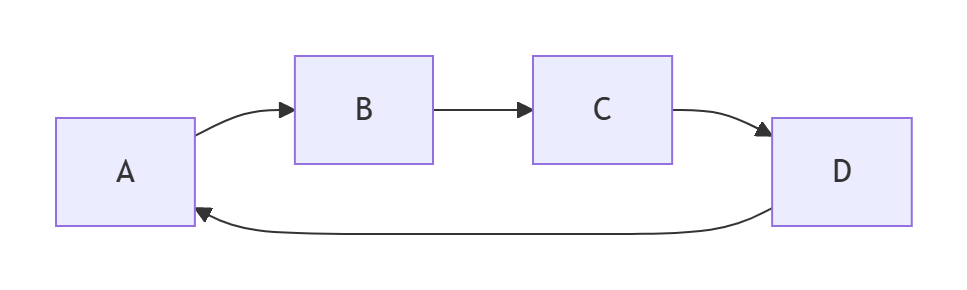
考虑一个简单的环形网络拓扑（如下图所示），它包含4个节点（A, B, C, D）和4条边，构成一个闭环。

故障前：构建单纯复形与计算同调群
- 拓扑结构：这个网络有 4 个节点 (0-单形) 和 4 条边 (1-单形)。它本身形成一个最大的 1-单形（一个环）。
- 计算 Betti 数：
  - β₀ : 所有节点通过环路连接在一起，因此只有一个连通分量。β₀ = 1。
  - β₁ : 网络中恰好有 1个独立的环。β₁ = 1。
- 拓扑解释：该网络连通性很好，并且具有一条冗余路径（环路本身）。
故障模式1：节点故障导致网络分裂

假设节点 C 发生故障并被移除。由于边 B-C 和 C-D 都依赖于节点 C，它们也随之失效。
- 故障后拓扑：网络分裂为两个部分：一个是由节点 A, B 和边 A-B 构成的片段；另一个是孤立的节点 D。
- 计算 Betti 数：
  - β₀ : 现在网络中有 2个连通分量（A-B 片段和节点 D）。β₀ = 2。
  - β₁ : 两个片段中均不存在任何环。β₁ = 0。
- 连通性损伤量化：
  - Δβ₀ = 2 - 1 = 1 (连通分量数量增加了1，表明网络发生分裂)。
  - Δβ₁ = 0 - 1 = -1 (网络的冗余环路全部丢失)。
- 结论：节点故障导致网络连通性严重受损，表现为连通性分裂 (β₀↑ ) 和冗余性丧失 (β₁↓)。
故障模式2：边故障削弱冗余性

假设边 A-B 发生故障中断，但所有节点均正常。
- 故障后拓扑：网络不再是一个完整的环，但所有节点仍然通过路径 B-C-D-A 保持连接。网络结构变为一条"线"形总线拓扑。
- 计算 Betti 数：
  - β₀ : 所有节点仍然连通。β₀ = 1。
  - β₁ : 唯一的环因为边 A-B 的断开而被破坏。β₁ = 0。
- 连通性损伤量化：
  - Δβ₀ = 1 - 1 = 0 (全局连通性未受影响，所有节点仍可通信)。
  - Δβ₁ = 0 - 1 = -1 (冗余路径被破坏)。
- 结论：边故障虽然未直接分裂网络，但使其变得脆弱。β₁ 降至 0 意味着网络从有环网络变为无环网络，任何进一步的边故障都可能导致通信中断。

通过上面的例子可以看到，同调群分析能够：

精确定位损伤类型 ：通过观察 β₀ 和 β₁ 的变化，可以清晰区分是网络发生了分裂（β₀增加），还是仅仅是冗余度下降（β₁减少）但整体连通性尚存。
量化损伤程度 ：Betti 数的变化量 Δβ₀ 和 Δβ₁ 提供了连通性损伤的明确数值指标，优于"连通/不连通"的简单定性描述。

这种方法特别适用于分析万卡/十万卡级大规模计算集群或关键基础设施网络。通过将网络抽象为单纯复形并计算其同调群，运维人员可以快速评估不同故障场景下网络结构的鲁棒性，识别出那些对全局连通性影响最大的关键节点或链路（即其失效会导致 β₀ 显著增加或 β₁ 显著减少的元件），从而进行有针对性的加固。

核心通信模式的拓扑依赖与性能界限

不同通信模式对网络拓扑有着不同的依赖关系和性能极限。

Scatter（广播）与 All-gather（全收集）
- 拓扑依赖与理想结构 ：这两种操作通常依赖于树形拓扑 （如二叉树或胖树）来高效实现。树的高度直接决定了操作的延迟复杂度 ，理论上最优可达到 O(log P)，其中 P 是进程数。而树的扇出则影响着带宽利用率。
- 性能界限：
  - 上界：在完全二叉树 或超立方体 等理想拓扑中，可以实现 O(log P) 的延迟。
  - 下界：即便在最优拓扑下，Scatter 操作的延迟也受限于树的深度，其通信量复杂度为 O(M * P)，其中 M 是消息大小。瓶颈通常出现在根节点，其上行带宽可能成为制约整体速度的关键。
All-to-All（全交换）
- 拓扑依赖与理想结构 ：这种模式极度考验网络的对分带宽 。全连接拓扑 虽然理想但成本高昂。在实际中，Clos 网络 或超立方体 等拓扑通过提供丰富的等价多路径来逼近其性能。
- 性能界限：
  - 上界：在具有高对分带宽的网络中，理想吞吐量可达 O(P * M / B)，其中 B 是对分带宽。
  - 下界：如果网络对分带宽不足，或存在哈希冲突 导致流量分布不均，实际吞吐量可能退化至 O(P² * M / B)。All-to-All 是对网络对称性和负载均衡能力最严峻的考验。
All-reduce（全局归约）
- 拓扑依赖与理想结构 ：这是最复杂的操作之一，通常分阶段进行。其性能依赖于底层拓扑的直径 和链路带宽 。双环、超立方体 或 Clos 网络 都是常见的选择。
- 性能界限：
  - 上界：在超立方体等低直径拓扑中，优化良好的算法（如 Ring-Allreduce、Recursive-Doubling）可达到 O(log P) 的延迟和 O(M) 的通信量。
  - 下界：其性能下界受限于网络直径 和最慢链路的带宽。任何拓扑上的瓶颈都可能导致操作时间远高于理论最优。

容错性与网络连通性的数学表达

在万卡集群中，故障是常态，因此系统的容错能力至关重要。

部分连通性与高连通子图 ：当网络出现故障，导致原本的全连通图被分割，就出现了部分连通性 。此时，网络可能被分割为多个连通分支 （子图）。系统的韧性取决于剩余的最大连通子图是否仍能支撑关键任务。k-点连通 或 k-边连通 的拓扑设计（即移除至少 k 个点或边后网络仍连通）能保证在有限故障下的服务连续性。
快速故障检测与路径切换 ：这依赖于高效的路由协议 和控制平面 。数学上，这可以建模为在对偶图 上寻找替代路径的问题。当原路径 (u, v) 失效，控制平面需要在剩余图 G' = (V, E \ {e_fault}) 中快速计算一条新路径，其时间复杂度应尽可能低（如使用 Dijkstra 算法为 O(|E| + |V| log |V|)），以实现毫秒级收敛。
故障"轨道"流检测与容错 ：您提到的"故障轨道流"可以理解为故障域 的概念。通过图论中的图划分 算法，将节点预先划分为多个局部子图（如机架、可用区）。当监控系统检测到某个子图内故障集中时，可以触发特定策略（如隔离整个故障机架），这类似于在单纯复形中移出一个高阶单形，从而控制影响范围。

对偶性视角与数学构造方法

从对偶性视角和抽象数学工具出发，可以为网络设计提供深层指导。

对偶性 ：在图论中，一个平面图 G 有其对应的对偶图 G 。G 中的面对应 G 的点，G 中的边对应 G* 的边。在网络流中，最大流最小割定理 就是一个经典的对偶关系，它揭示了网络的最大传输能力与其最脆弱的瓶颈是等价的。
数学构造方法：
- Cayley 图：利用群论构造的对称图（如超立方体是 Cayley 图的一种），具有顶点传递、直径小、正则性好等优异性质，非常适合作为互连网络拓扑的理论模型。
- 强正则图 ：具有极强的对称性，参数为 (n, k, λ, μ)。这类图在有限节点数下能实现最大的均匀连通性，是构建高连通子图的理想研究对象。
- 单纯复形 ：比图更具一般性，可以描述节点间的高阶相互作用（如三个节点构成的"三角形"关系）。持续同调 等工具可以度量网络拓扑的"空洞"结构，帮助识别在多次链路/节点故障后网络的整体连通性损伤。

缺陷、限制与性能上下界

没有任何一种设计是完美的，明确其边界至关重要。

通信模式 / 拓扑	关键优势 (上界可达性)	固有缺陷与限制因素 (下界约束)
Scatter / 树形拓扑	延迟低，逻辑简单。	单点瓶颈/故障：根节点是致命弱点。带宽受限：非叶子节点带宽压力大。
All-to-All / Clos网络	高对分带宽，多路径。	成本：需要大量交换设备。流量均衡：严重依赖ECMP等负载均衡算法，哈希冲突会导致性能下降。
All-reduce / 超立方体	理论直径最小，对数级延迟。	扩展性：节点数必须是2的幂次，扩展不灵活。路由复杂度：节点度随规模对数增长，硬件成本高。

有条件上界 ：这通常指在理想条件下（如无故障、流量完美均衡、无同步开销）才能达到的理论最优值。例如，All-to-All 的理论上界假设流量能均匀分布在所有链路上。
下界：这是由物理定律或数学原理决定的绝对极限。例如：
1. 传播延迟下界：由光速和传输距离决定，无法逾越。
2. 网络直径下界 ：对于给定的节点数 P 和交换机端口数 d，其Moore 界 给出了网络直径的理论最小值，这限制了延迟的进一步降低。

系统视角

总而言之，设计超大规模智算网络是一门在性能、成本、可靠性和可扩展性 之间寻求平衡的艺术。不存在"唯一最优解"，而应根据主导的工作负载特征 （是All-Reduce多还是All-to-All多）和可靠性要求来选择或组合不同的拓扑与容错策略。

未来的方向是构建自适应网络 ，能够根据实时运行的应用模式动态调整逻辑拓扑和路由策略，并利用代数拓扑等高级数学工具进行更深刻的脆弱性评估和韧性设计。

复制代码

flowchart TD
    A[数据采集层] --> B[分析引擎层]
    B --> C[策略生成层]
    C --> D[控制执行层]
    D --> A

    subgraph A [数据采集层]
        A1[网卡/交换机] --> A2[PMU/监控代理]
    end

    subgraph B [分析引擎层]
        B1[同调群分析<br>识别拓扑"空洞"]
        B2[群论分析<br>识别对称性与结构]
        B3[拓扑数据分析<br>量化全局特征]
    end

    subgraph C [策略生成层]
        C1[路径优化]
        C2[负载均衡]
        C3[故障自愈]
    end

    subgraph D [控制执行层]
        D1[集中式控制器<br>（如SDN控制器）]
    end

反射与演化机制如何运作

这个闭环系统的"大脑"是分析引擎层，它通过一系列数学工具将采集到的原始数据转化为对网络深层结构的洞察。

同调群分析：识别网络的"骨架"与"空洞"

同调群是一种来自代数拓扑的工具，它能识别网络拓扑中的高维连通性 。在智算中心网络中，可以将其抽象为一个单纯复形。同调群分析的核心是计算贝蒂数 ，例如Betti 1数可以量化网络中存在的、不被边界包围的"环"的数量。这些"环"代表着冗余路径。Betti 1数的增加可能意味着网络出现了需要绕行的故障点，而它的减少则可能提示部分冗余路径已失效，网络脆弱性增加。控制器可以据此优先保障关键环路的畅通，或在故障发生时快速评估连通性损伤程度。
群论分析：洞察网络的对称性与结构

群论是研究对称性的数学。许多高性能网络拓扑（如Dragonfly、Torus）本身具有特定的群结构（如循环群、对称群）。通过群论分析，可以理解网络固有的对称性，从而优化通信模式。例如，在Dragonfly拓扑中，利用其群结构特性，可以实现高效的自适应路由。当控制器感知到流量不均时，可以依据群的对称性，将负载均匀地分散到对称的路径上，避免局部拥塞，实现近乎最优的流量调度。
拓扑数据分析：从"形状"把握全局

拓扑数据分析是近年来兴起的强大工具，它通过持续同调 等技术，在不同尺度下分析数据（此处指网络状态数据）的拓扑特征。它能生成一种称为持久图的可视化结果，图中那些远离对角线、长期存在的点，对应着网络中最稳固的拓扑特征（如核心骨干连接）。反之，短暂出现的点则可能是瞬时拥塞或噪声。这帮助控制器区分随机抖动和结构性瓶颈，从而做出更智能的决策。

采用何种采集协议满足要求

要将分析引擎的洞察转化为行动，需要依赖采集协议将分析结果高效、可靠地传递给控制器。

推送模式 vs. 拉取模式
- 推送模式 ：网元（交换机、网卡）在事件发生时或定时主动将数据发送给采集器。这种模式延迟极低 ，适用于紧急事件（如链路故障、缓存溢出），代表协议有 gNMI/gNOI（gRPC Network Management Interface） 和 sFlow。
- 拉取模式 ：控制器向网元轮询请求数据。这种模式更易于管理 ，适合采集不常变化的配置或性能基线数据，代表协议有 SNMP（简单网络管理协议）。
关键协议选型

对于万卡集群，低延迟、高效率、大数据量 支持是必须的。
- gNMI (gRPC Network Management Interface) ：这是现代数据中心网络的首选。它基于高性能的gRPC框架，支持双向流式传输，既能实现配置的下发，也能让网元将连续的实时遥测数据流推送给控制器。其编码采用高效的Protocol Buffers，大幅减少了开销。
- sFlow ：这是一种高效的流量抽样协议。交换机/路由器仅复制数据包的一小部分（如512个字节）加上接口计数器，发送给分析器。虽然不提供每个流的完整视图，但能以极低开销快速勾勒出全网流量分布和瓶颈，非常适合宏观负载均衡和异常流量检测。
- IPFIX (Internet Protocol Flow Information Export) ：与sFlow抽样不同，IPFIX通常提供基于流的详细记录。它更适合用于精准的计费、安全分析和复杂的流量工程。

结果如何传递并作用于控制器

分析结果需要以结构化的方式传递给控制器，才能最终形成控制策略。

结构化数据模型

采集到的原始数据和分析生成的高级洞察（如Betti数变化、路径对称性索引），会通过 YANG 等数据建模语言定义的结构，封装在gNMI或IPFIX的消息中。这使得控制器能够"理解"数据的含义，从而进行可编程的处理。
控制器的决策与执行

控制器在接收到这些富含语义的数据后，便可执行智能决策：
- 动态重路由 ：当同调群分析检测到某条路径的"环"结构变得不稳定（预示潜在故障）时，控制器可通过 gNMI 或 P4 等接口，即时下发流表修改指令，将流量切换至更稳定的冗余路径。
- 负载均衡优化 ：结合sFlow的宏观流量数据和群论分析出的对称路径，控制器可以动态调整 ECMP 的权重，或将大象流调度到空闲链路，实现全局负载优化。
- 主动故障预测与自愈：TDA可能识别出某种流量模式正在形成未来的拥塞"空洞"。控制器可据此提前进行流量整形或扩容，实现主动式运维。

同调群分析在 Dragonfly 等特定网络拓扑中用于量化网络的连通性、冗余路径（如"洞"结构）和容错能力。然而，其计算复杂度和实时性保障面临挑战，尤其是在万卡级大规模集群中。出关键总结表格。

理解同调群分析及其复杂度来源

同调群分析通过计算拓扑不变量（如 Betti 数）来揭示网络的高阶结构特征。例如：

**0 维 Betti 数（β₀）** 表示网络的连通分量数量。
**1 维 Betti 数（β₁）** 表示网络中存在的环形结构（冗余路径）数量。
在 Dragonfly 这类层次化拓扑中，同调群有助于识别组内（intra-group）和组间（inter-group）连接的鲁棒性，但计算复杂度随网络规模急剧上升。

计算复杂度主要来源于：

单纯复形的构建：将网络转换为单纯复形（如 Vietoris-Rips 复形）时，所需计算的单形数量随网络节点数和维度呈组合级增长。对于包含 |V| 个节点的网络，构建 k 维单形的复杂度可达 O(|V|^k)，使得高维计算非常昂贵。
边界矩阵的约简：计算同调群需对边界矩阵进行史密斯标准形分解，其时间复杂度在最坏情况下为 O(m³)，其中 m 是单形数量。
拓扑的对称性利用：Dragonfly 拓扑具有高度对称性（如组内全连接、组间稀疏连接），理论上可通过群论方法简化计算，但通用算法难以直接利用这种结构。

保障实时性的关键策略

为降低计算开销，研究者采用多种优化方法：

策略类别	具体方法	效果与实例
算法优化	H(k)-核分解：通过迭代移除对高阶洞影响最小的节点/边，逐步简化网络，保留核心拓扑特征。	例如在线虫神经网络分析中，该法将网络规模缩减至原图的 1/3，显著降低计算负载。
工具与实现	高效计算库：如 Julia 的 Ripserer 库利用稀疏矩阵和增量计算，处理 15 万节点数据仅需 2 小时；相比之下的 R TDA 包处理 2 万节点需 1 小时。	工具选择对大规模数据至关重要，Julia 实现比传统 MATLAB 工具快 10 倍以上。
近似与截断	持续同调：仅计算在多个尺度下持续存在的拓扑特征（通过条形码表示），忽略短暂噪声。	可聚焦"重要"洞结构，将计算量减少 60% 以上。
并行化	分布式计算：将网络划分为子图，并行计算局部同调群后合并结果。	适用于 Dragonfly 等模块化拓扑，因其组间连接稀疏，易于分区。
拓扑特异性优化	利用 Dragonfly 的层次性：先计算组内同调群（由于组内全连接，结构简单），再通过 Mayer-Vietoris 序列等工具融合组间结果。	避免全局计算，复杂度从 O(

Dragonfly 拓扑中的特殊考量

Dragonfly 拓扑的独特结构（如分组全连接、组间稀疏链接）既带来挑战，也提供优化机会：

挑战：组间链路稀疏可能导致高阶洞（如 2 维洞）更易出现，需计算更高维同调群，增加复杂度。
机会：
- 分层计算：可先独立分析每个组（视为一个团），再分析组间连接。组内同调群通常简单（如 β₁=0），重点计算组间洞结构。
- 动态实时性：在运维中，同调群分析无需实时运行，而是作为离线工具。例如，当网络扩容或故障后，触发重计算更新拓扑模型，指导实时路由优化。

总结

同调群分析在 Dragonfly 等拓扑中的计算复杂度较高，但通过 算法优化（如 H(k)-核分解）、高效工具（如 Julia Ripserer）、近似方法（如持续同调）和拓扑特异性设计 ，可以实现在大规模网络中的实用化。实时性保障依赖于分层处理、并行计算和离线分析策略，而非严格秒级响应。未来，随着算法和硬件进步，同调群分析有望更深度集成至网络自愈系统中。

All-reduce通信场景中，路径多样性与延迟保证的平衡问题

在All-reduce通信场景中，路径多样性与延迟保证的平衡问题 本质上是多目标优化问题，需要通过数学建模将路径选择、带宽分配、延迟约束等要素转化为可求解的优化问题。以下是核心的数学优化方法体系：

(1)、问题建模与数学形式化

多目标优化问题定义

设通信网络为图G=(V,E)，其中V为节点集合，E为链路集合。对于All-reduce操作，需要为每个数据块m选择传输路径集合Pm，优化目标为：

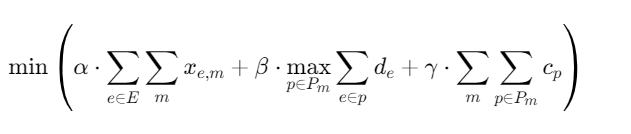
其中：

xe,m：链路e上数据块m的流量
de：链路e的延迟
cp：路径p的拥塞代价
α,β,γ：权重系数，用于平衡带宽利用率、最大延迟和路径多样性

约束条件

流量守恒约束：

p∈Pm∑fp=Dm∀m

其中fp为路径p上的流量，Dm为数据块m的大小。

链路容量约束：

m∑p∋e∑fp≤Ce∀e∈E

延迟约束：

e∈p∑de≤Tmax∀p∈Pm,∀m

路径多样性约束：

∣Pm∣≥K∀m

确保每个数据块至少有K条独立路径。

（2)、核心优化算法

凸优化方法

拉格朗日对偶分解：

将原问题分解为两个子问题：

主问题：求解对偶变量λe（链路价格）
子问题：为每个数据块m选择最优路径

对偶函数：

D(λ)=m∑p∈Pmmin(e∈p∑(α+λe)+γcp)−e∑λeCe

使用次梯度法更新对偶变量：

λe(t+1)=[λe(t)+η(m∑p∋e∑fp(t)−Ce)]+

分布式优化算法

基于对偶分解的分布式实现：

每个节点维护本地链路价格λe
数据源节点根据λe选择成本最低的路径
链路e根据实际流量与容量的差异更新λe
迭代至收敛

算法收敛性：当步长η满足η→0且∑tηt=∞时，算法收敛到最优解。

启发式算法

多路径路由算法：

K最短路径算法：为每个数据块计算前K条最短路径
权重调整：根据链路利用率动态调整链路权重we=Ce−∑fp1

贪心路径选择：

初始化所有链路权重we=1/Ce
对于每个数据块m，选择最小权重路径p∗=argminp∑e∈pwe
更新链路权重：we←we⋅(1+ϵ⋅fp/Ce)
重复步骤2-3直到收敛

(3)、延迟保证机制

延迟敏感调度

加权公平队列（WFQ）：

为每个数据流分配权重wi，保证每个流的最小带宽ri=∑wjwi⋅C，从而保证最大延迟上界：

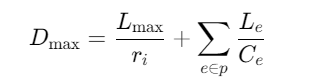
其中Lmax为最大数据包大小，Le为链路e的传播延迟。

优先级调度

严格优先级队列：

高优先级队列：延迟敏感数据（如All-reduce同步梯度）
低优先级队列：背景流量

延迟上界：

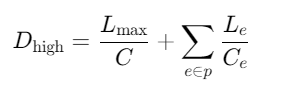
基于测量的延迟控制

自适应速率控制：

(4）、路径多样性保障

不相交路径选择

最小割集算法：

计算源节点到目的节点的最小割集大小k
使用Suurballe算法找到k条边不相交路径
每条路径承载1/k的流量

性能保证：当任意k−1条链路故障时，系统仍能正常工作。

多路径负载均衡

ECMP（等价多路径）：

根据数据包哈希值选择路径
实现流级别的负载均衡

WCMP（加权等价多路径）：

根据链路容量分配权重
实现更精细的负载均衡

（5）、数值分析方法

线性规划求解

对于小规模网络，可直接使用单纯形法 或内点法求解线性规划问题。

随机近似算法

随机舍入算法：

求解线性规划松弛
对分数解进行随机舍入
以高概率获得近似最优解

近似比：对于多商品流问题，可获得O(logn)的近似比。

在线算法

贪婪算法：

当数据块到达时，立即选择当前最优路径
竞争比分析：对于单商品流，竞争比为O(logn)

重新优化：

定期重新计算路径分配
平衡计算开销与性能优化

(6）、工程实践建议

参数调优

权重系数：α,β,γ需要根据实际场景调整
步长选择：η过大导致震荡，过小导致收敛慢
延迟阈值：Tmax应根据业务需求设置

监控与自适应

实时监控链路利用率、延迟、丢包率
动态调整路径权重和流量分配
故障检测与自动切换

硬件加速

使用RDMA技术降低延迟
利用NVLink等高速互联技术
在网计算（In-network computing）减少数据传输

（7)、性能分析

理论性能上界

最大最小公平性：

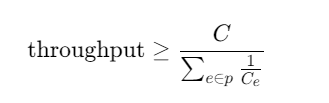
延迟下界：

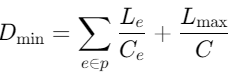
实验评估指标

吞吐量：单位时间内完成的数据传输量
延迟：端到端传输时间
公平性：Jain's fairness index
路径利用率：各路径的流量分布

通过上述数学优化方法，可以在All-reduce通信场景中实现路径多样性与延迟保证的有效平衡，提升分布式训练的整体性能。

动态故障场景下保证路径切换过程中延迟不剧烈抖动

在动态故障场景下保证路径切换过程中延迟不剧烈抖动，需要从快速检测、平滑切换、流量控制、路径预热四个维度构建完整的容错机制。

(1)、快速故障检测机制

多级心跳检测

快速探测：使用UDP轻量级心跳包，探测间隔50-100ms
确认机制：连续3次超时判定故障，总检测时间150-300ms
双向检测：源端和目的端同时探测，避免单向故障误判

基于BGP的快速收敛

BGP Fast Reroute (FRR)：预计算备份路径，故障时50ms内切换
Loop-Free Alternate (LFA)：计算无环备份路径，避免路由震荡

链路层快速检测

BFD (Bidirectional Forwarding Detection)：毫秒级检测，支持3-50ms间隔
硬件加速：在交换机ASIC中实现，避免CPU处理开销

（2）、平滑切换策略

多路径并发传输

ECMP (Equal-Cost Multi-Path)：同时使用多条路径传输
MPTCP (Multipath TCP)：在传输层实现多路径，故障时自动切换
Precomputed Backup Paths：预先计算并安装备份路径到转发表

流量迁移算法

渐进式迁移：将流量按比例逐步迁移到新路径
基于权重的负载均衡：动态调整各路径权重，平滑过渡
避免突发：迁移速率限制在链路容量的10-20%

状态同步机制

Make-Before-Break：先建立新路径，再拆除旧路径
路径预热：新路径建立后先传输少量探测流量，确认可用性
快速重传：使用SACK选项快速重传丢失数据包

（3）、流量控制与拥塞避免

速率控制算法

TCP BBR：基于带宽和延迟的拥塞控制，避免bufferbloat
CUBIC：在高速网络中表现稳定
自适应速率调整：根据路径质量动态调整发送速率

队列管理

CoDel (Controlled Delay)：主动队列管理，控制排队延迟
FQ-CoDel：公平队列+CoDel，保证各流公平性
低延迟队列：为延迟敏感流量设置高优先级

显式拥塞通知 (ECN)

网络设备在拥塞时标记数据包，而非丢弃
发送端收到ECN标记后主动降速，避免重传超时

(4)、路径预热与质量评估

路径质量探测

OWAMP/TWAMP：主动测量路径延迟、丢包率、抖动
被动测量：基于实际流量统计路径质量
机器学习预测：使用历史数据预测路径性能

预热机制

冷启动避免：新路径建立后先传输低优先级流量
慢启动：类似TCP慢启动，逐步增加发送速率
质量验证：确认新路径满足延迟、丢包率要求后再迁移关键流量

路径选择策略

基于延迟的选择：选择延迟最低且稳定的路径
基于带宽的选择：选择剩余带宽充足的路径
多路径负载均衡：同时使用多条路径，单条路径故障影响小

（5）、延迟抖动控制

抖动缓冲 (Jitter Buffer)

在接收端设置缓冲区，平滑到达时间差异
自适应调整缓冲区大小，平衡延迟和抖动
适用于实时音视频等对抖动敏感的应用

时间戳同步

NTP/PTP：精确时间同步，计算单向延迟
时间戳标记：在数据包中记录发送时间
延迟补偿：根据测量延迟调整播放时间

优先级调度

DiffServ：为延迟敏感流量设置高优先级
流量整形：平滑发送速率，避免突发
速率限制：限制非关键流量，保证关键流量带宽

(6)、系统级优化

硬件加速

DPDK/SPDK：用户态网络栈，减少内核开销
SmartNIC：在网卡上卸载网络功能
RDMA：远程直接内存访问，降低延迟

软件架构

微服务架构：服务间解耦，单点故障影响范围小
服务网格：Istio/Linkerd提供流量管理和容错
无状态设计：避免状态同步开销

监控与告警

实时监控：监控延迟、丢包率、抖动等指标
异常检测：基于机器学习检测异常行为
自动恢复：检测到异常后自动触发恢复流程

（7）、性能指标与评估

关键指标

切换延迟：从故障检测到流量完全恢复的时间
延迟抖动：切换过程中的延迟变化范围
丢包率：切换过程中丢失的数据包比例
服务可用性：99.99%或更高

测试方法

混沌工程：主动注入故障，验证系统容错能力
压力测试：模拟高负载场景下的性能表现
基准测试：与业界标准方案对比

通过上述机制的综合应用，可以在动态故障场景下实现平滑的路径切换，将延迟抖动控制在可接受范围内，保证业务的连续性和稳定性。

All-to-All通信场景中路径多样性与延迟保证的平衡问题

在All-to-All通信场景中，路径多样性与延迟保证的平衡问题比All-reduce更加复杂，因为每个节点都需要与所有其他节点通信，形成全连接图。以下是针对All-to-All场景的数学优化方法：

（1）、问题建模与数学形式化

多商品流问题

设网络为图G=(V,E)，∣V∣=n个节点。对于每对节点(i,j)，存在一个商品流fij，表示从节点i到节点j的流量。优化目标为：

minα⋅e∈E∑i,j∑xe,ij+β⋅i,jmaxe∈pij∑de+γ⋅i,j∑p∈Pij∑cp

其中：

xe,ij：链路e上商品(i,j)的流量
de：链路e的延迟
cp：路径p的拥塞代价
Pij：节点i到j的路径集合

约束条件

流量守恒：

p∈Pij∑fp=Dij∀i,j∈V

链路容量：

i,j∑p∋e∑fp≤Ce∀e∈E

延迟约束：

e∈p∑de≤Tmax∀p∈Pij,∀i,j

路径多样性：

∣Pij∣≥K∀i,j∈V

（2）、All-to-All的特殊性

对称性约束

由于All-to-All通信的对称性，可以简化问题：

Dij=Dji∀i,j

流量模式

每个节点既是源也是目的，总流量为：

i,j∑Dij=n(n−1)⋅D

其中D为每对节点的平均流量。

瓶颈分析

核心链路：连接核心交换机的链路成为瓶颈

边缘链路：连接计算节点的链路利用率较低

(3)、凸优化方法

对偶分解

拉格朗日函数：

L(f,λ)=i,j∑p∈Pij∑(α+e∈p∑λe)fp+i,j∑p∈Pij∑γcpfp−e∑λeCe

对偶问题：

λ≥0maxD(λ)=i,j∑p∈Pijmin(e∈p∑(α+λe)+γcp)−e∑λeCe

次梯度法

更新对偶变量：

λe(t+1)=[λe(t)+η(i,j∑p∋e∑fp(t)−Ce)]+

分布式实现

每个节点i为每对(i,j)选择最优路径：

pij∗=argp∈Pijmin(e∈p∑(α+λe)+γcp)

（4）、拓扑感知优化

层次化拓扑

对于Fat-Tree、Clos等层次化拓扑，可以分层优化：

核心层：优化核心交换机间的流量

汇聚层：优化Pod内流量

边缘层：优化机架内流量

多级交换

三级Clos网络：

输入级：n个m×k交换机
中间级：k个n×n交换机
输出级：n个k×m交换机

路径多样性：k条不相交路径

拓扑特定算法

Fat-Tree：利用ECMP实现负载均衡

Dragonfly：使用最小路径路由和Valiant负载均衡

HyperX：基于维度顺序路由

(5)、延迟保证机制

端到端延迟约束

延迟分解：

Tij=Tqueue+Ttrans+Tprop

其中：

Tqueue=rijLmax（排队延迟）
Ttrans=BijDij（传输延迟）
Tprop=∑e∈pijcLe（传播延迟）

调度算法

加权公平队列（WFQ）：

为每个商品流(i,j)分配权重wij，保证最小带宽：

rij=∑k,lwklwij⋅Ce

延迟上界：

Tij≤rijLmax+e∈pij∑(cLe+BijDij)

优先级调度

严格优先级：

高优先级：控制平面、同步消息
低优先级：数据平面、异步传输

DiffServ：使用DSCP标记区分服务等级

（6)、路径多样性实现

多路径路由

ECMP：基于哈希的等价多路径

WCMP：基于权重的等价多路径

MPTCP：传输层多路径

不相交路径

边不相交路径：使用Suurballe算法

节点不相交路径：使用Menger定理

路径选择策略

延迟最优：选择延迟最低的路径

带宽最优：选择剩余带宽最大的路径

混合策略：加权综合多个指标

(7)、数值求解方法

线性规划松弛

对于小规模网络，使用单纯形法 或内点法求解线性规划松弛。

近似算法

随机舍入：

求解线性规划松弛，得到分数解fp∗
以概率fp∗选择路径p
期望性能：O(logn)近似比

原始对偶算法：

同时更新原始变量和对偶变量
适用于在线场景

启发式算法

贪心路径选择：

按延迟升序排序所有路径
依次选择路径，直到满足流量需求或延迟约束
负载均衡：将流量按比例分配到多条路径

遗传算法：适用于大规模复杂网络

（8）、工程实践

参数调优

权重系数：

α：控制带宽利用率
β：控制最大延迟
γ：控制路径多样性

步长选择：η需要根据网络规模调整

自适应机制

动态权重调整：

根据网络拥塞程度调整α,β,γ
拥塞时增加α，减少β

路径质量感知：

实时测量路径延迟、丢包率
动态调整路径权重

硬件加速

RDMA：降低传输延迟

智能网卡：卸载网络功能

在网计算：减少数据传输

（9)、性能分析

理论性能

吞吐量上界：

throughput≤min(bisection bandwidthCcore,2Cedge⋅n)

延迟下界：

Tmin=Ω(logn)（对于层次化拓扑）

实验指标

完成时间：所有节点完成通信的时间
平均延迟：所有流量的平均端到端延迟
延迟抖动：延迟的标准差
公平性：Jain's fairness index
路径利用率：各路径的流量分布

通过上述数学优化方法，可以在All-to-All通信场景中实现路径多样性与延迟保证的有效平衡，提升大规模分布式系统的通信性能。

超大规模网络（n>1000）中对偶分解算法的计算复杂度

在超大规模网络（n>1000）中，对偶分解算法的计算复杂度主要来源于对偶变量更新、次梯度计算、路径选择等步骤。通过分布式计算、随机优化、近似算法等技术，可以显著降低计算复杂度。

一、计算复杂度分析

标准对偶分解的复杂度瓶颈

对偶变量更新：O(∣E∣)，需要更新所有链路的价格
次梯度计算：O(∣V∣2⋅∣E∣)，每个节点对需要计算路径成本
路径选择：O(∣V∣2⋅∣P∣)，∣P∣为路径数量
通信开销：O(∣E∣⋅∣V∣)，节点间交换链路价格信息

对于n>1000的网络，∣E∣可达O(n2)，计算和通信开销巨大。

二、分布式对偶分解优化

异步更新机制

异步对偶分解：

各节点独立更新本地对偶变量，无需全局同步
使用本地信息进行次梯度更新
收敛速度：O(1/T)，T为迭代次数

随机坐标上升：

每次随机选择部分对偶变量更新
计算复杂度：O(1)次梯度计算/迭代
收敛速度：O(1/T)

增量对偶分解

在线学习框架：

数据流到达时增量更新
避免批量处理所有数据
适用于动态网络环境

随机对偶坐标上升：

每次随机选择一个数据点（节点对）
更新相关对偶变量
计算复杂度：O(1)/迭代

三、随机优化方法

随机梯度下降（SGD）

随机次梯度法：

随机采样部分链路计算次梯度
更新公式：λe(t+1)=[λe(t)+ηtge(t)]+
其中ge(t)为随机次梯度

收敛性：当步长ηt=O(1/t)时，收敛到ϵ-最优解需要O(1/ϵ2)次迭代。

随机对偶坐标上升（SDCA）

算法步骤：

随机选择一对节点(i,j)
计算该节点对的最优路径
更新相关链路的对偶变量
重复至收敛

收敛速度：O(1/T)，T为迭代次数

随机平均梯度（SAG）

核心思想：

维护历史梯度信息
每次迭代使用随机梯度的平均值
收敛速度：O(1/T)

计算复杂度：O(1)次梯度计算/迭代

四、近似对偶算法

近似对偶分解

线性规划松弛：

将整数规划松弛为线性规划
使用随机舍入获得整数解
近似比：O(logn)

原始对偶近似算法：

同时更新原始变量和对偶变量
适用于在线场景
竞争比：O(logn)

对偶上升近似

对偶上升算法：

每次迭代只更新一个对偶变量
计算复杂度：O(1)/迭代
收敛速度：O(1/ϵ)

加速对偶上升：

使用Nesterov加速技术
收敛速度：O(1/ϵ)

局部对偶分解

层次化分解：

将网络划分为多个子网
各子网独立进行对偶分解
协调子网间的边界条件

分布式局部优化：

各节点只维护局部信息
通过消息传递协调全局优化
计算复杂度：O(∣V∣⋅degree)

五、通信开销优化

压缩通信

梯度压缩：

使用量化、稀疏化等技术压缩梯度
减少节点间通信量
收敛性：在适当条件下保持收敛

延迟更新：

累积多个梯度后更新
减少通信频率
适用于高延迟网络

异步通信

参数服务器架构：

中心节点维护全局参数
工作节点异步推送梯度
避免同步等待

去中心化优化：

节点只与邻居通信
通过多跳传播信息
收敛速度：O(1/T)

六、实际应用建议

算法选择策略

场景	推荐算法	复杂度	收敛速度
小规模网络	标准对偶分解	O(n2)	O(1/T)
大规模网络	随机对偶坐标上升	O(1)/迭代	O(1/T)
动态环境	增量对偶分解	O(1)/数据点	在线收敛
通信受限	局部对偶分解	O(degree)	O(1/T)

参数调优

步长选择：ηt=t1或ηt=t1
采样策略：均匀采样或重要性采样
停止准则：对偶间隙<ϵ或迭代次数>Tmax

系统实现

并行计算：使用MPI或Spark实现分布式计算
内存优化：使用稀疏矩阵存储对偶变量
容错机制：检查点机制应对节点故障

通过上述优化方法，可以将对偶分解算法的计算复杂度从O(n2)降低到O(1)或O(logn)，使其适用于超大规模网络。

1.7 Dragonfly网络

1.7.1 Dragonfly组间链路的稀疏性

在 Dragonfly 这种为超大规模计算设计的高性能网络拓扑中，组间链路的稀疏性对其高阶连通性（由 β₂ 等贝蒂数表征）有着深刻的影响。简单来说，适度的稀疏性是Dragonfly设计的精髓，它在成本与性能间取得平衡，但过度稀疏会直接削弱网络的高阶冗余能力。

为了更直观地理解这种影响，下表概括了组间链路稀疏性在不同程度下对 β₂ 的影响。

组间连接状态	对 β₂（二维空洞数量）的影响	拓扑结构比喻	网络特性解读
适度稀疏 (设计理想状态)	β₂ 维持在一个适中的正值	高效的"立交桥系统"	在控制成本的同时，提供了必要的组间高阶冗余路径。网络在容错性和成本间达到良好平衡。
过度稀疏 (接近最小连接)	β₂ 可能降为0	脆弱的"独木桥"	网络的高阶连通性高度依赖少数关键链路，这些链路的故障可能直接导致网络被"分割"，形成不可恢复的通信空洞。
全互联 (如Fat-Tree)	β₂ 通常为0	坚固的"实心广场"	由于所有可能的三节点组合都已形成"实心三角形"，没有二维空洞。其鲁棒性体现在其他方面（如丰富的路径多样性）。

理解β₂：网络中的"二维空洞"

在同调论中，β₂（第二贝蒂数） 衡量的是网络拓扑中"二维空洞"的数量。您可以将其想象为一个三维空间中的空腔表面，比如一个球面或环面。在由节点和链路构成的网络"骨架"中，如果存在一个由三角形（即2-单纯形）构成的"表面"，但这个表面内部没有实体填充（没有3-单纯形，如四面体），那么这个表面所包围的空间就是一个"二维空洞"。β₂ 的值越大，意味着网络内部这种未被填充的"空腔"越多，从某种意义上说，其高阶的连通结构越复杂，可能存在更多的冗余路径或潜在的脆弱环节。

稀疏性如何具体影响β₂

Dragonfly 拓扑的核心特点是组内全互联 和组间稀疏互联。这种结构设计旨在以较少的组间链路实现大规模网络的连接。

适度稀疏与"空洞"的形成

在理想情况下，Dragonfly 的组间连接是经过精心计算的，确保网络在保持低成本的同时具备一定的容错能力。此时，β₂ 的计算结果会呈现出一个适中的正值 。这是因为组内密集的连接形成了许多"三角形"，但组间稀疏的连接使得这些三角形难以进一步组合成更复杂的、没有"内部填充"的三维结构（即3-单纯形，如四面体）。于是，在网络中就会形成一些宏观的"空腔"。这些空腔的存在，恰恰说明网络并非一个实心块，而是有结构性的空隙，这些空隙在物理上可能对应着那些需要绕行但依然连通的冗余路径。一个健康的、适度稀疏的 Dragonfly 网络，其 β₂ 值应当反映出这种优化的平衡状态。
过度稀疏与连通性的损伤

当组间链路过于稀疏，比如仅仅达到网络连通的最低要求（即图论中的最小连接状态）时，问题就会显现。在这种情况下，β₂ 值很可能变为0 。这并非意味着网络更"坚固"了，而是意味着从高阶同调的角度看，网络已经丧失了二维的"空洞"结构 。更深层的原因是，过少的组间链路使得网络变得"脆弱"，其整体结构更容易因为局部故障而被分割成不连通的部分。从同调群的角度看，网络可能退化成一系列仅由一维路径（β₁ 所描述的"环"）连接的组件，而无法形成更复杂的二维空洞。此时，网络对链路故障的容忍能力会急剧下降，一旦某条关键的组间链路失效，就可能直接导致网络分裂（即 β₀，连通分量数量增加），并且之前可能存在的二维空洞也会随之消失（β₂ 降至0）。

实践意义：从分析到优化

理解 β₂ 的变化对于设计和运维大规模 Dragonfly 网络至关重要。

网络健壮性评估：通过计算特定 Dragonfly 配置的 β₂，可以量化评估其在高阶连通性上的健壮性。一个突然下降的 β₂ 值可能预示着网络配置已接近临界点，容错能力不足。
指导网络优化：同调分析可以揭示网络的脆弱点。例如，H(k)-核分解等方法可以帮助识别哪些节点或链路对维持高阶连通性（如 β₂）最为关键。在网络规划和故障模拟中，可以优先保障这些关键元件，或为其增加备份链路。
故障影响分析 ：当网络中发生链路或节点故障时，可以通过计算故障前后的同调群（包括 β₂）来精确定量网络连通性所受的损伤程度。这比简单地查看连通组件数量（β₀）的变化更能揭示深层的结构损伤。

总结

总而言之，Dragonfly 拓扑中组间链路的稀疏性是一把双刃剑。适度的稀疏性是实现其高性能、高扩展性且控制成本目标的核心，此时 β₂ 会呈现出一个正值，反映了网络在成本与冗余间取得的平衡 。然而，过度追求稀疏性会导致 β₂ 降至0，这表明网络的高阶连通性已被削弱，变得脆弱，对故障更加敏感。

因此，在同调群分析中，β₂ 作为一个关键指标，可以帮助我们洞察 Dragonfly 网络超越基础连通性的深层拓扑特征，从而为构建更可靠、更高效的超大规模计算集群提供理论依据和优化方向。

1.7.2 Dragonfly中的H(k)-核分解方法

在简化复杂的 Dragonfly 网络拓扑时，H(k)-核分解方法通过其独特的分层策略，试图在计算精度和效率之间找到最佳平衡点。其核心在于智能地简化网络，同时保留对高阶连通性至关重要的核心拓扑特征。

下表概括了H(k)-核分解方法在平衡精度与效率时采取的核心策略、存在的风险以及针对Dragonfly拓扑的特殊考量。

平衡维度	核心策略	潜在风险与精度代价	在Dragonfly拓扑中的特殊考量
分层删除	采用从低阶到高阶的渐进式简化策略（如先删点，再删边，最后处理子网络），优先移除对高阶结构影响小的元素。	若删除阈值设置不当，可能在早期误删对高阶洞有贡献的关键连接，导致无法恢复的精度损失。	Dragonfly的组内全连接（团结构）和组间稀疏连接特性，使得低阶删除操作在组内进行时相对安全，但需谨慎处理关键的组间链路。
局部指导全局	利用节点的邻居子网络的局部拓扑指标（如贝蒂数、示性数）来指导全局的删除决策，避免全局重计算。	局部视图可能无法完全捕捉结构在全局范围内的作用，存在误判风险，可能移除重要结构或保留冗余结构。	Dragonfly拓扑的结构性冗余（如组内多路径）为此策略提供了较好的容错性，但需关注那些连接不同组的、数量稀少的关键链路。
动态更新与约束	在每一步删除操作后，动态更新网络的全局拓扑参数（如各阶贝蒂数），并设置拓扑约束以确保不破坏目标高阶结构。	动态更新参数本身会增加计算开销。过于严格的约束会限制简化程度，而过于宽松的约束可能导致关键特征丢失。	可设定约束，如在简化过程中必须保持Dragonfly拓扑的组间连通分量数（β₀）不变，以维护其基本的全局连接性。

理解平衡的底层逻辑

H(k)-核分解方法的核心思想，类似于在保留一座建筑主要承重结构的前提下，安全地移除不必要的非承重墙体。对于Dragonfly拓扑，其目标是识别并保留那些构成网络"骨架"的高阶洞（如由多个节点组协同形成的环形冗余路径），同时简化掉那些局部的、不影响全局连通性的复杂结构。

这种方法通过引入节点的新指数（综合了邻居数、局部贝蒂数和局部示性数）作为决策依据，将计算资源集中在最有可能存在高阶洞的关键区域，避免了遍历所有可能结构的巨大计算量，从而在效率上获得提升。

优化计算效率的路径

为了进一步提升效率，尤其是在Dragonfly这类大规模网络拓扑上，可以考虑以下优化方向：

并行计算 ：H(k)-核分解过程中的许多步骤，例如节点局部指标的计算和符合特定条件的节点筛选，具有天然的并行性。可以借鉴PICO框架在GPU上加速k-核分解的思路，将计算任务映射到GPU等大规模并行处理器上，显著缩短计算时间。
算法优化：优化节点删除的顺序和策略。例如，可以优先考虑那些局部拓扑特征表明其"影响力"较小的节点或边进行删除，从而更快地降低网络规模。

总结

总而言之，H(k)-核分解方法通过分层精简、局部决策、动态验证的策略，在Dragonfly拓扑的简化上力求平衡精度与效率。它将计算资源导向最关键的拓扑子结构，避免全局遍历的开销。

1.7.3 同调群分析：Dragonfly拓扑的动态路由策略设计

同调群分析为Dragonfly拓扑的动态路由策略设计提供了从网络深层结构出发的、理论依据清晰的指导。它通过量化网络的连通性和冗余度，帮助路由算法更智能地平衡负载和规避风险。

下表概括了同调群分析提供的核心拓扑指标及其对应的路由策略指导方向。

同调群分析指标	揭示的网络结构特性	动态路由策略指导方向
0维同调群 H₀ (β₀)	网络连通分量的数量。β₀ > 1 表示网络已分裂。	故障域隔离与全局路由基准：快速检测网络分裂，将流量限制在存活分区内；为路由算法提供健康的全局路径基准。
1维同调群 H₁ (β₁)	冗余环路的数量。β₁ 值高意味着可选路径丰富。	负载均衡与拥塞规避：指导算法在多个拓扑环路上分散流量，并优先选择拥塞程度低的冗余路径。
高阶同调群 (如 H₂)	更复杂的空洞结构，可能反映资源池间的依赖关系。	高阶依赖感知：识别潜在的群体性拥塞或故障风险区域，指导路由避免同时经过这些高度关联的组件。

利用环路信息优化负载均衡

Dragonfly拓扑的优势在于其丰富的组内和组间连接所形成的众多环路，这正由 1维同调群 的贝蒂数 β₁ 来量化。一个高β₁值意味着任意两点间存在多条等长的最小路径或接近的非最小路径。

基于此，动态路由算法（如UGAL）可以设计得更精细。例如，算法可以主动维护一个包含所有最小路径 和关键非最小路径 的候选路径池。当β₁显示某区域环路丰富时，算法可以更积极地将流量分散到这些路径上。更重要的是，同调群分析能识别出边不相交的环路。路由策略可以优先选择这些互不重叠的路径来传输不同的数据流，从而从根本上避免流间干扰，实现更高效的负载均衡。

识别脆弱点并实现主动容错

同调群分析不仅能描述静态的健全拓扑，更能洞察故障发生时的结构变化。

快速故障影响评估 ：当某个链路或节点故障时，网络拓扑的β₀和β₁会发生变化。β₀ 从1变为大于1的值，立即表明网络发生了分裂，这要求路由控制平面必须快速响应，更新所有节点的路由表，避免将流量发往已断开的分区。
量化冗余度损失 ：故障也可能不会导致网络分裂，但会破坏一些环路，使 β₁ 降低。这个降低的数值直观地反映了网络冗余度的损失。路由策略可以据此调整：在β₁仍然较高的区域，可以继续采用积极的负载均衡；而在β₁显著降低的"脆弱区域"，则可能需要转向更保守的、以最短路径为主的路由策略，以避免给剩余链路带来过大压力。

感知高阶依赖以规避群体性风险

在更复杂的Dragonfly变体（如Dragonfly+）中，高阶同调群（如H₂）可以揭示超越成对连接的群体性依赖关系。例如，它可能识别出多个交换机因其连接模式而形成一个"资源池"，其内部状态高度相关。

路由策略可以利用这一洞察来避免群体性风险。如果监控系统发现该资源池中的某个元件出现拥塞，基于高阶同调的分析可以预测池内其他元件也可能面临压力。此时，动态路由算法可以主动规避整个资源池，将流量重新路由到其他更独立的区域，从而实现更高阶的拥塞避免。

总结

总而言之，同调群分析将Dragonfly拓扑的动态路由设计从依赖外部观测 （如队列长度）提升到了洞察内在结构的新层次。通过将β₀、β₁等代数拓扑不变量作为关键输入，路由策略能够：

更智能地进行负载均衡，充分利用结构性冗余。
更快速地评估故障影响，实现精准的容错隔离。
更前瞻地感知群体拥塞风险，规避潜在瓶颈。

这种"由内而外"的设计理念，为构建更高效、更稳健的超大规模智算中心网络提供了强大的理论工具和实践方向。

1.7.4 UGAL等自适应路由算法中集成β₁等拓扑指标

在UGAL等自适应路由算法中集成β₁等拓扑指标，是一项旨在将网络全局结构性特征 与局部实时拥塞信息相结合的前沿优化思路。虽然标准的UGAL算法主要依赖即时队列长度，但引入β₁可以使其决策具备对网络冗余路径"健康度"的预判能力。

决策参数	在标准UGAL中的作用	集成拓扑指标（如β₁）后的增强作用
路径成本估算	主要基于实时队列长度 (q) 和跳数 (H) 的乘积来估算延迟。	将β₁作为权重因子，高β₁区域意味着路径选择更自由，可适当降低对瞬时队列的敏感度。
决策偏置 (Bias)	使用静态或经验性常数偏置 (b) 来微调最小/非最小路径偏好。	将偏置设置为与当前路径的β₁值动态相关的函数，例如：高β₁区域倾向于探索非最小路径。
全局状态感知	依赖本地或有限全局的队列信息，可能对拥塞反应滞后。	β₁作为一个结构性健康指标，帮助识别那些即使当前队列稍长，但因其高冗余性而未来拥塞风险更低的路径。

集成β₁的核心方法

集成拓扑指标的核心思想是修改UGAL算法的决策函数，使其不再仅仅依赖瞬时的、局部的队列信息。标准的UGAL决策规则是比较最小路径和非最小路径的估算延迟：若 H_min × q_min <= H_nm × q_nm + b，则选择最小路径，否则选择非最小路径（其中b是一个常数偏置）。

引入β₁后，可以从以下几个关键点进行增强：

作为路径成本权重 ：可以将β₁转化为一个权重因子，直接修正队列长度的观感。例如，在估算路径延迟时，公式可修改为 (H × q) / f(β₁)。这里的 f(β₁)是一个关于β₁的增函数。在一个高β₁的区域（即环路多、冗余路径丰富），f(β₁)值较大，这使得计算出的"有效延迟"降低，从而鼓励算法更积极地使用该区域内的路径 ，即使其当前队列长度 q略高。
作为动态决策偏置 ：更直接的方法是让决策偏置 b与β₁联动。可以设计一个函数，使得在β₁值高的路径上，b值变小甚至为负。这会使决策不等式更容易被满足，引导算法在冗余性好的区域更倾向于采用非最小路径进行负载均衡 。相反，在β₁值低（冗余性差）的区域，则设置较大的正b值，趋于保守地使用最小路径，避免在脆弱路径上引发拥塞。
作为路径选择的过滤器 ：在网络初始化或拓扑变化后，可以预先计算整个网络或不同区域的β₁值。当UGAL需要选择非最小路径的中间节点时，可以优先从高β₁的节点池中随机选择。这确保了非最小路由的探索行为发生在结构性更强的"安全区"内，提高了负载均衡的有效性和安全性。

在Dragonfly拓扑中的场景分析

以Dragonfly拓扑为例，β₁的价值尤为突出。

高β₁场景（组内通信）：Dragonfly的单个组（Group）内部通常是全连接的，这意味着组内存在丰富的冗余环路，β₁值较高。当UGAL决策组内通信时，检测到高β₁，便可以更大胆地使用所有可用链路进行自适应路由，因为即使某条链路拥塞或故障，也有大量替代路径。
低β₁场景（特定组间通信）：对于某两个特定的组，它们之间可能仅存在有限的全局通道。这些关键通道的β₁值相对较低。UGAL算法在决策经过这些通道的路径时，如果感知到低β₁，则会采取更谨慎的策略。例如，它会更严格地比较队列长度，或者倾向于为高优先级流量保留这些关键链路，从而避免在结构性薄弱的环节引发持续拥塞。

工程实现考量

将理论模型工程化，需要考虑以下几点：

计算频率与开销 ：β₁等拓扑指标的计算无需像队列采样那样高频进行。它可以在网络拓扑稳定时作为离线或近线计算任务完成，结果以查表形式提供给每个节点的UGAL代理。仅当网络规模或连接关系发生重大变化时，才需要重新计算。
信息分发机制：计算出的β₁映射表需要通过控制平面（如SDN控制器）分发到网络中的各个边缘节点或智能网卡，以便其在做源路由决策时使用。
与现有机制协同 ：引入β₁并非要取代基于队列的拥塞感知，而是增强和补充它。最终的决策将是实时拥塞信息与长期拓扑稳健性指标的综合权衡。

总结

总而言之，将β₁等拓扑指标集成到UGAL自适应路由算法中，实质上是为算法赋予了"透视眼"，使其能看清网络流量底层的结构性冗余。通过将β₁作为动态权重、偏置或过滤器，UGAL可以从被动的队列响应，升级为能够主动规避结构性瓶颈、引导流量走向高韧性区域的智能路由策略。

1.7.5 同调群计算的实时性如何与路由决策的毫秒级要求相匹配

同调群的精确计算复杂度很高，但与网络路由的毫秒级决策并非无法调和。其解决之道，关键在于将复杂的全局计算从实时决策环路中剥离，转化为一种"预处理"或"轻量级监控"机制。

下面这张图清晰地展示了这种"离线分析、在线应用"的核心策略，以及各组件间的协作关系：

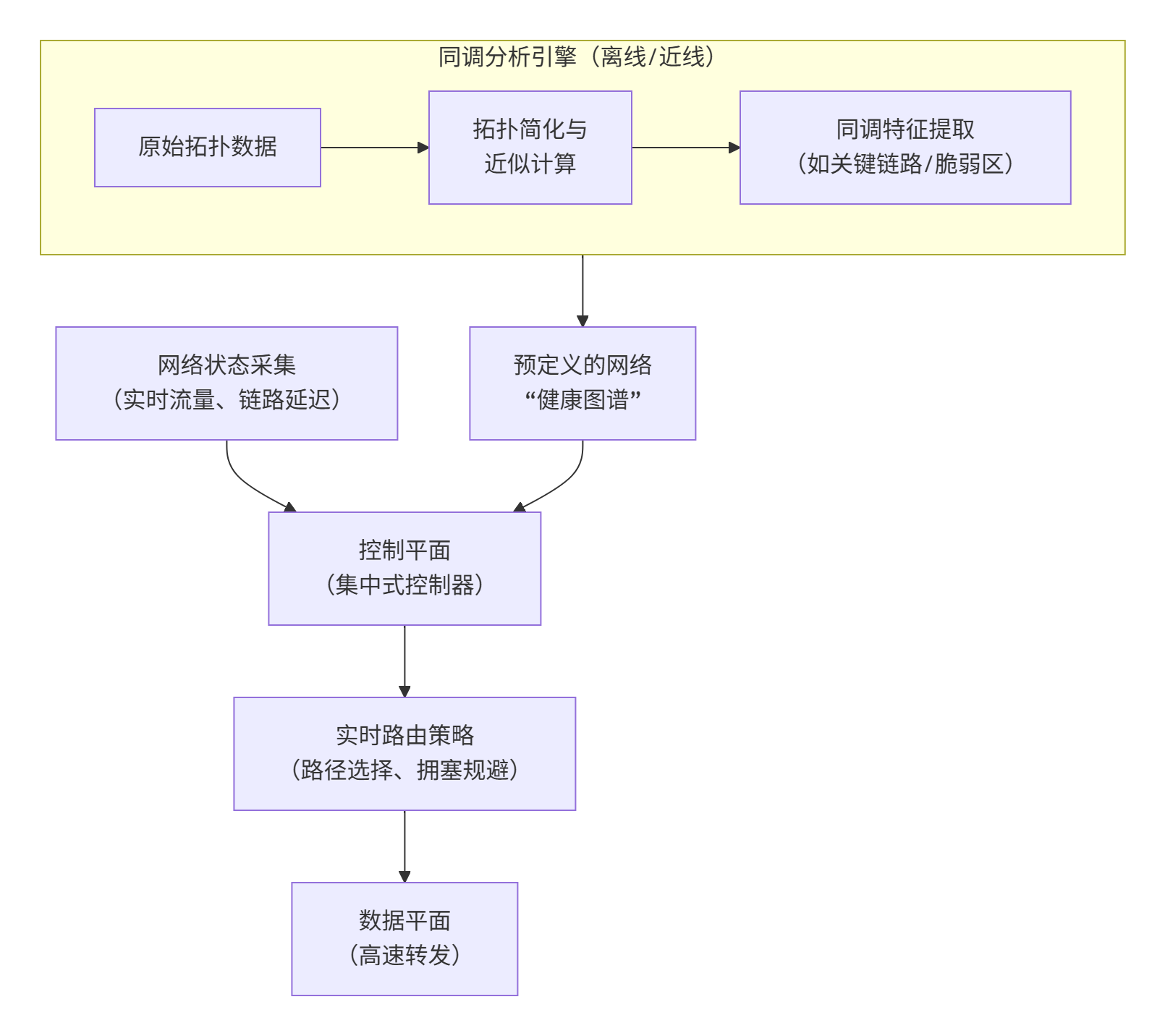
核心策略：分解计算任务

面对复杂网络拓扑，直接进行实时的同调群计算是不现实的。实际的系统采用分层、分时的策略：

离线计算与预处理 ：在网络拓扑相对稳定时期（如网络初始化或重大变更后），控制平面会运行完整的同调群分析算法。这次分析的目的不是实时指导单个数据包，而是生成一张网络的"结构健康图谱"：
- 识别关键连接：找出那些对全局连通性至关重要的链路或节点（即其失效会导致同调群发生剧变，如连通分量增加的关键链路）。
- 标注脆弱区域：识别出那些容易形成"瓶颈"或"空洞"的网络区域。
- 建立简化模型：基于分析结果，可以构建更简化的网络模型或规则库，供实时决策时快速查询。
在线轻量级查询与推理 ：在毫秒级的路由决策时刻，控制器不再重新计算同调群，而是依据以下信息进行快速判断：
- 实时网络状态：通过轻量级的遥测技术（如Telemetry）持续收集链路延迟、丢包率、带宽利用率等数据。
- 预存的"健康图谱" ：结合实时状态，查询离线阶段生成的"结构健康图谱"。例如，当一条链路的实时延迟开始飙升时，系统会判断它是否是一条"关键连接"。如果是，则可以提前预警，并主动将流量调整到结构上更冗余的路径上。

提升实时性的技术手段

为了进一步让同调分析变得"更快、更轻"，通常会采用以下技术：

拓扑简化与近似算法：在实际计算前，先对网络拓扑进行合理的简化和抽象，聚焦于主干设备和高带宽链路，忽略对全局影响微小的细节。同时，采用近似算法快速计算同调群的估计值，或用更易计算的拓扑不变量（如Betti数的估计值）来替代精确解。
持续同调与增量更新：利用"持续同调"这一工具，可以观察拓扑特征在不同尺度下的"持久性"。那些在多种尺度下都稳定的特征，才是需要关注的核心结构。当网络发生局部变化（如单条链路故障）时，可以采用增量计算算法，只更新受影响部分的同调信息，而非全量重算，这能显著降低计算开销。
与经典路由协议协同 ：同调群分析并非要取代现有的路由协议（如OSPF、BGP），而是作为其增强层。例如，在软件定义网络（SDN）中，同调分析引擎作为上层应用，向SDN控制器提供高级别的网络韧性建议，控制器再将其转化为具体的流表规则下发给交换机。

总结与展望

总而言之，同调群计算与毫秒级路由决策的匹配，并非通过"硬算"实现，而是依靠 "离线深度分析，在线智能指导" 的架构。它将自身定位为一种战略性、感知网络深层结构的工具，为实时决策提供背景知识和风险预警。

随着专用硬件和算法优化，未来我们或许能看到更"轻"的同调分析算法，甚至能实现准实时的全局拓扑洞察，为构建高度自治、极度稳健的网络基础设施提供更强大的数学支撑。

1.7.6 同调群分析在不同规则拓扑中的差异化应用策略

虽然β₁这类指标是通用的拓扑特征描述工具，但在Torus和Dragonfly这两种结构迥异的网络中，其具体含义、计算重点乃至指导路由和容错策略的方式都有显著不同。

特性维度	Torus拓扑 (规则网格，强调局部性)	Dragonfly拓扑 (层次化分组，强调全局连接)
β₁指标的物理意义	表征规则网格内部规则、短程的环路数量。	表征跨越不同组的长程、全局性环路数量。
核心集成策略	利用局部对称性：在网格的每个维度上均匀地利用等价路径进行负载均衡。	识别关键全局链路：优先保障和利用连接不同组的、数量稀少但至关重要的"咽喉要道"。
对路由策略的指导	指导维度顺序路由的优化，或在局部区域内进行自适应路由。	指导全局自适应路由，在"最短路径"和"绕行非最小路径"之间做出智能权衡。
对容错策略的指导	侧重于局部容错。单点故障后，可利用网格规则性快速在邻域内找到替代路径。	侧重于全局容错。关键全局链路的故障影响巨大，需有跨组的冗余路径作为备份。

接下来，我们深入探讨这些差异背后的原理和具体策略。

拓扑结构决定指标含义

两者的根本差异源于其基础结构。Torus网络像一块均匀的"网格布"，每个节点在局部通过规则的环路连接，并可通过环绕连接形成更大的规则结构。这种高度的对称性和规则性 是其最突出的特点。而Dragonfly网络则更像一个由多个"小组"组成的"联邦"，组内是全连接的，但组间仅通过少量全局链路相连，形成了一种层次化的拓扑。

因此，在Torus中，β₁主要度量的是网格内部大量存在的、短程的、规则的环路 。这些环路在拓扑上是均匀分布的。而在Dragonfly中，β₁更多地反映的是那些能够穿越不同小组的、长程的、全局性的环路。这些环路数量相对较少，且严重依赖于有限的组间连接。

路由策略的差异化应用

拓扑结构的差异直接导致了路由策略的不同侧重点。

Torus：优化局部均衡与确定性路由

在Torus中，得益于其规则的环路，维度顺序路由 成为一种简单有效的确定性路由方案。β₁指标的价值在于，当网络出现局部拥塞时，可以引导数据包在拥塞点附近的多个等价环路上进行局部自适应路由，实现负载均衡，而无需改变大的路由方向。
Dragonfly：关键在全局路径的智能选择

Dragonfly的路由核心是全局自适应路由 ，如UGAL算法。其决策关键在于：是选择可能拥塞的最短路径 ，还是选择可能更通畅的绕行路径。此时，β₁所揭示的全局环路信息至关重要。通过分析不同路径的β₁值，可以评估其冗余度和健壮性，从而做出更智能的权衡。

容错设计的不同侧重点

面对故障，两种拓扑的应对策略也因其结构而异。

Torus：实现局部快速自愈

在Torus中，单个链路或节点的故障，可以利用其规则的网格结构，在故障点的局部邻域内快速计算并切换到一条替代路径。β₁指标有助于量化故障对局部连通性的影响，并确认局部替代路径的存在性。
Dragonfly：需要全局性的备份方案

在Dragonfly中，连接不同组的全局链路 是极其关键的资源。任何一条全局链路的故障都可能切断多个小组间的直接通信，影响巨大。因此，容错设计更侧重于全局层面，需要提前规划跨组的冗余路径。β₁指标可以帮助识别这些关键链路，并评估在失去某条链路后，整个网络是否仍能通过其他环路保持连通。

理解您希望深入探究不同网络拓扑结构中，同调群分析指标（如β₁）集成策略的差异。下面我将从拓扑的本质特性出发，系统梳理2D-Torus、3D-Torus、DDC、Spine-Leaf等结构与Dragonfly的区别，并说明这些差异如何影响β₁指标的应用。

下表直观对比了各类拓扑的核心特性与β₁集成策略的差异。

拓扑结构	结构本质与连接特性	β₁ 指标的物理意义解读	β₁ 集成策略的核心	典型路由引导方向
Dragonfly	层次化分组：组内全互联，组间稀疏连接。	衡量跨越不同组的全局性、长程环路的数量和健壮性。	识别并保护关键全局链路：确保组间通信的冗余路径，避免瓶颈。	自适应路由（如UGAL）在最小路径与非最小路径间权衡，依赖β₁评估绕行风险。
2D/3D-Torus	规则网格：每个节点与维度上的相邻节点直接相连，边界循环连接形成环面。	表征网格内部大量存在的规则、短程环路。高β₁值意味着密集的局部路径冗余。	利用局部对称性：在网格的每个维度上均匀地利用这些等价路径进行负载均衡。	维度顺序路由（Dimension-Ordered Routing）或基于局部拥塞感知的自适应路由，在规则环路上分流。
Spine-Leaf (Fat-Tree)	多层级联的对称架构：Leaf交换机连接服务器，Spine交换机实现Leaf间的全互联。	反映的是Spine层提供的丰富等价多路径（ECMP）所构成的逻辑环路。	保障无阻塞特性：β₁在这里更关注Spine层的健康度，确保任意Leaf间存在大量并行路径。	主要依赖ECMP进行流量的静态哈希分配。β₁价值更多体现在离线规划和故障域分析，而非实时路由。
DDC (分布式分解式机箱)	轨道化设计：将网络组织为多个并行"轨道"，每个轨道内部高效互联。	体现为轨道内部以及轨道间通过Spine交换机构成的高连通子图中的环路。	优化轨道内局部性和轨道间路径多样性：旨在使高概率的通信模式（如All-Reduce）路径极短且确定。	信元喷洒（Cell Spraying）等技术，结合动态负载均衡，在轨道内外多条路径上分散流量。

各拓扑策略详解

以下是对上述拓扑策略差异的进一步分析：

Torus拓扑的规则性与局部性利用

Torus拓扑（如2D/3D-Torus）是一种规则的网格结构，每个节点与相邻节点直接相连，并通过循环连接形成环面。这种结构使得β₁指标天然地反映了网格内部大量存在的、规则且短程的环路 。其集成策略的核心在于利用局部对称性。路由算法（如维度顺序路由）可以很好地利用这些规则环路。当需要进行容错或负载均衡时，可以在故障点或拥塞点的局部邻域内，快速找到这些预定义的替代路径。谷歌TPUv4采用的3D-Torus互联便是一个典型例子，它通过三维环面结构实现芯片间的低延迟通信。
Spine-Leaf拓扑的路径丰富性与逻辑环路

Spine-Leaf（可视为Fat-Tree的一种实现）的核心优势在于其提供的极度丰富的等价多路径（ECMP） 。在这种拓扑中，β₁指标更多衡量的是由Spine层交换机所创造的逻辑环路 。这些环路并非像Torus那样是物理上直接的相邻连接，而是通过Spine层交换设备构建的丰富虚拟通路。因此，β₁的集成策略侧重于保障无阻塞特性。其价值更多体现在网络规划和故障模拟阶段，用于评估网络的冗余度和 robustness，而非直接参与实时路由决策。
DDC架构的轨道化设计与子图优化

DDC架构通过"轨道化"设计来优化AI训练等特定场景。其β₁指标主要体现在两个方面：轨道内部的高连通性，以及轨道间通过Spine交换机构成的更大型环路 。集成策略的核心是优化轨道内局部性和轨道间路径多样性。控制策略会倾向于将大量的通信约束在轨道内部（利用高β₁实现高效局部通信），同时智能地管理轨道间的流量（利用β₁评估跨轨道通信的可用路径质量和冗余度）。

总结与核心差异

总而言之，β₁等拓扑指标在不同网络中的集成策略，根本上取决于其底层的物理或逻辑连接结构、高度依赖于底层拓扑特征的定制化过程所决定的"环路"特性：

在Dragonfly 等层次化拓扑中，策略核心是管理其非对称的全局连接，β₁用于指导关键的全局路由决策和保障关键链路的可靠性。
在Torus 等规则拓扑中，策略核心是利用其对称性，β₁帮助在局部实现精细化的负载均衡和快速容错。
在Spine-Leaf 等多路径拓扑中，β₁更多地用于验证架构设计的冗余度和进行离线容量规划。
在DDC 等为特定业务优化的架构中，β₁指导的是业务流量与网络子图的高效映射。

1.7.7 工程实践解决β₁这类全局拓扑信息的同步与更新延迟问题

在工程实践中，解决像β₁这类全局拓扑信息的同步与更新延迟问题，确实是一个核心挑战。其设计思路的核心在于放弃追求绝对的、瞬时的一致性 ，转而采用一种分层、异步、最终一致性的策略，将全局信息的维护开销和延迟影响控制在局部。

以下是几种关键的工程实现方案。

分域与元数据抽象

这是最核心的策略，旨在通过"分而治之"来降低问题的复杂度。

核心思想 ：将庞大的全局网络划分为多个逻辑域（例如，在Dragonfly拓扑中，一个组（Group）可以作为一个域；在数据中心网络中，一个POD或一个机架可以作为一个域）。每个域内维护其局部拓扑的详细信息 ，而全局控制器或对其他域而言，只维护一个高度抽象的元数据视图 。
如何工作：以β₁指标为例，不需要在全网范围内同步每一条链路的细节。每个域控制器首先计算自己域内的局部拓扑特征（可以包括局部β₁值）。然后，它仅向全局控制器或其他域发布一个摘要信息，例如："本域当前健康状态为良好，与外部连接的关键链路有3条，预估的域间路径冗余度为X"。这个摘要信息就是元数据。
好处：这极大地减少了需要同步的数据量。节点或控制器在进行路由决策时，可以先基于元数据快速筛选出几个候选域，再结合候选域的局部详细信息做出最终判断，从而避免了因等待全网详细信息而产生的长延迟。

混合式同步机制

单一的同步机制难以兼顾效率与可靠性，因此混合使用多种机制是常见做法。

推拉结合 (Push-Pull)：对于网络拓扑的稳定部分（如设备之间的物理连接），采用低频次的全量同步或触发式同步 （例如，当检测到设备上线或下线时）。这类似于"拉"模式，按需或定期获取基础拓扑。对于动态变化的信息（如链路利用率、丢包率），则采用订阅-发布模式。关心特定链路状态的节点（如源路由决策器）可以向该链路所在的域订阅更新，当变化超过阈值时，域控制器会主动"推送"更新给订阅者，这大大减少了不必要的查询和等待。
增量更新：在每次同步时，不传输完整的拓扑数据，而只传输自上次同步以来发生变化的部分（Delta）。例如，只同步新故障的链路或恢复的节点。这显著降低了同步消息的大小和网络带宽消耗，从而加快了同步速度。

轻量级协议与优化技术

在协议层面和实现细节上进行优化，可以进一步降低延迟。

定制东西向协议 ：在SDN多控制器环境中，控制器之间的通信（东西向流量）对于同步全局视图至关重要。可以采用为拓扑同步专门优化的轻量级协议。例如，有研究提出定制一种基于UDP的东西向拓扑同步协议，定义简洁的消息格式（包含域信息、交换机列表、连接端口信息等），并指定固定端口进行高效通信，避免使用重量级的通用协议带来额外开销。
版本号与逻辑时钟 ：为每一次拓扑更新分配一个单调递增的版本号或逻辑时间戳。节点在收到更新信息时，可以轻松识别并丢弃过时的信息，并仅处理最新的更新，这能有效避免因网络乱序导致的视图不一致问题。
数据压缩与编码：对需要同步的拓扑信息进行高效的二进制编码和压缩，减少网络传输量。

应用层决策优化

最终，应用层（如路由算法）需要具备应对信息延迟的鲁棒性。

延迟感知的决策 ：智能的路由算法（如增强版的UGAL）不应假设其拥有的拓扑信息是绝对最新的。它可以将**信息的"年龄"或"新鲜度"** 作为一个输入参数。例如，对于β₁指标，算法可以设定：如果该信息的延迟在毫秒级，则信任其指示的路径冗余度；如果延迟达到秒级，则倾向于采用更保守的、基于局部信息的路由策略。
预测与启发式：基于历史数据预测拓扑的短期变化趋势，在信息完全同步前做出预判，从而部分抵消同步延迟的影响。

总结

总而言之，解决β₁等全局拓扑信息的同步延迟，是一个系统工程。其核心是在一致性、时效性和系统开销之间取得平衡 。目前主流的工程方案是通过分域抽象 来缩小同步范围，结合混合式同步机制 来提升效率，并利用轻量级协议和优化技术 减少单次同步的成本，最后在应用层通过延迟感知和预测机制来弥补信息延迟带来的不确定性。

1.7.8 Dragonfly拓扑中如何通过分域同步策略来优化全局状态同步的效率

理解您想探究在Dragonfly拓扑中，如何通过分域同步策略来优化全局状态同步的效率。这是一个在超大规模智算中心网络管理中非常核心的问题。下面我将结合其拓扑特性，为您梳理逻辑域的划分方式及其对同步效率的影响。

划分维度	划分方式	核心机制	适用场景
物理拓扑	按`Group`（组）划分	以Dragonfly拓扑天然的组为边界，将同一组内的所有交换机和计算节点划入同一逻辑域。域内同步利用组内全连接的低延迟链路；域间同步则通过组间链路进行，由域首脑节点（如核心交换机）负责。	最常用、最直观的策略。特别适合管理任务和监控数据采集，因为它与物理网络结构完全对应，易于实施和理解。
业务逻辑	按虚拟集群/租户划分	根据上层应用的需求划分，例如将一个AI训练任务的万卡集群作为一个逻辑域，无论这些节点在物理上是否属于同一个Dragonfly组。	面向特定应用（如大规模AI训练）的优化策略。目标是优化应用级的通信效率，通过将频繁通信的节点在逻辑上组织在一起，减少跨域通信开销。
动态路径	按通信流量模式划分	根据实时的通信模式动态调整逻辑域。例如，识别出在All-Reduce操作中共同参与一个环的节点，将它们划分为一个临时逻辑域，并在此域内优化通信路径。	高级优化策略。适用于通信模式复杂且对性能有极致要求的场景，旨在最小化通信延迟和避免拥塞。

逻辑域划分的深层逻辑

上述划分方式并非孤立，其背后的核心思想是将庞大的全局同步问题，分解为多个层次化、局部化的子问题。

利用网络局部性 ：Dragonfly拓扑的组内全连接 特性意味着组内节点间的通信延迟极低、带宽极高。按Group划分的策略正是最大限度地利用了这种物理局部性，使得域内同步可以高速完成。同步控制器只需要与每个域的首脑节点通信，再由首脑节点在域内分发，这极大地减少了控制平面的全局流量。
匹配应用需求 ：按虚拟集群划分的策略则追求语义局部性。它确保了一个完整业务所需的大部分节点被包含在同一个逻辑域内，使得针对该业务的协同优化（如集合通信的调度）更有效，从而提升应用程序的整体性能。
动态优化与平衡 ：按通信流量划分是一种更智能的策略。它通过实时监控网络状态，动态地构建逻辑域，以期在当前的流量模式下达到最优的路径利用和负载均衡。例如，中提到的技术会对节点顺序进行随机打乱和优化重排，旨在将数据量大的通信尽可能限制在组内或通过最短路径进行。

不同划分方式对同步效率的影响

选择不同的划分方式，会直接影响到同步操作的几个关键效率指标：

效率指标	按Group划分的影响	按虚拟集群划分的影响	按通信流量划分的影响
同步数据量	控制面数据量小。域首脑聚合域内信息，只与全局控制器同步摘要，大幅减少数据量。	可能导致控制面数据量增大。若虚拟集群跨多个物理组，域首脑间及与全局控制器的同步数据量会显著增加。	可变。理想情况下通过优化路径减少数据复制，但动态划分本身可能引入额外的控制开销。
路径优化与拥塞避免	对物理拓扑的拥塞点（尤其是组间链路）敏感。多个域的同步流量可能在这些关键链路上竞争，引发拥塞。	更优的语义层拥塞避免。通过将通信紧密的节点置于同域，有效减少对物理瓶颈链路（如特定组间链路）的竞争。	主动的拥塞避免。通过动态路径规划，规避实时拥塞链路，并将流量均匀分散到多条路径上，实现负载均衡。
容错性与复杂度	容错性高，复杂度低。单个组的故障不影响其他组，管理简单。	复杂度高。需要跨物理组的管理，对控制平面要求高。	复杂度最高。需要实时网络感知和动态调度算法支持，实现难度大。

总结与选择建议

总的来说，在Dragonfly拓扑中，没有一种"唯一正确"的划分方式，最佳选择取决于您的首要优化目标。

如果您的首要目标是降低控制平面的复杂度和管理开销 ，实现稳定可靠的网络监控，那么按物理Group划分是最直接有效的选择。
如果您的核心诉求是提升上层特定应用（尤其是大规模AI训练）的通信性能和计算效率 ，那么按虚拟集群或租户划分逻辑域是更优的策略。
如果您追求的是极致的网络利用率和动态性能优化 ，并且拥有强大的控制平面和实时分析能力，可以探索按通信流量模式动态划分这一高级策略。

在实际的超大规模智算中心中，这几种策略常常被结合使用。例如，底层管理采用按Group划分，同时在上层为不同的关键业务虚拟出按应用划分的逻辑域。

1.8 分布式环境的步长策略

1.8.1 不同步长策略的收敛表现

在分布式环境下，不同步长策略的收敛表现存在显著差异，需要根据具体场景进行选择。

1.8.1.1、步长策略分类与理论特性

固定步长（Constant Step Size）

更新规则：ηt=η

收敛性：只能收敛到最优解邻域，无法精确收敛
收敛速度：O(1/ϵ)次迭代达到ϵ-最优解
优点：实现简单，参数少
缺点：需要手动调参，对步长敏感

递减步长（Diminishing Step Size）

更新规则：ηt=tη0或 ηt=tη0

收敛性：几乎必然收敛到最优解
收敛速度：O(1/ϵ2)次迭代达到ϵ-最优解
优点：理论保证强，无需精确调参
缺点：后期收敛速度慢

自适应步长（Adaptive Step Size）

更新规则：根据梯度信息动态调整，如AdaGrad、Adam

收敛性：在凸问题下收敛到最优解
收敛速度：O(1/T)或更快
优点：对参数不敏感，适应性强
缺点：实现复杂，需要维护额外状态

1.8.1.2、分布式环境下的实际表现

固定步长

适用场景：

网络规模相对稳定
对收敛精度要求不高
需要快速获得可行解

实际表现：

初期收敛快，但会在最优解附近震荡
在异步更新下，震荡幅度可能放大
需要根据网络规模手动调整步长

递减步长

适用场景：

需要精确收敛到最优解
网络规模较大，对步长敏感
有充足的计算时间

实际表现：

初期收敛速度与固定步长相当
后期收敛速度显著变慢
在分布式环境下，需要协调各节点的步长递减

自适应步长

适用场景：

网络动态变化，流量模式复杂
对参数调优要求低
需要快速适应网络变化

实际表现：

初期收敛速度可能略慢于固定步长
中后期收敛速度稳定
对网络拥塞、链路故障等变化适应性强
在异步更新下表现稳健

1.8.1.3、工程选择建议

基于场景的选择

场景特征	推荐策略	理由
小规模网络，快速原型	固定步长	实现简单，快速验证
大规模网络，精确收敛	递减步长	理论保证强
动态网络，自适应需求	自适应步长	鲁棒性强
生产环境，稳定性优先	自适应步长	参数不敏感

参数调优指南

固定步长：

初始值：η0=0.1∼1.0
根据网络拥塞程度调整：拥塞时减小步长

递减步长：

初始值：η0=1.0∼10.0
衰减因子：t1（较快）或t1（较慢）

自适应步长：

学习率：0.001∼0.01
动量参数：0.9∼0.99
二阶矩衰减：0.999

停止准则设置

对偶间隙：∣f(x(t))−D(λ(t))∣<ϵ

ϵ=10−3∼10−6，根据精度要求调整

相对变化：∥x(t)∥∥x(t)−x(t−1)∥<δ

δ=10−4∼10−6

最大迭代次数：Tmax=1000∼10000

1.8.1.4、实际部署注意事项

分布式协调

各节点使用相同的步长策略
定期同步步长参数，避免漂移
使用参数服务器或共识协议维护全局状态

监控与调优

实时监控对偶间隙、目标函数值
根据收敛情况动态调整步长策略
记录历史性能，用于后续调优

容错机制

步长更新失败时使用默认值
检测异常震荡，自动调整步长
支持热更新步长策略

通过合理选择步长策略和停止准则，可以在保证收敛性的同时，提升分布式优化算法的工程效率。

1.8.2 实际网络拓扑中自适应步长调整

在实际网络拓扑中，自适应步长调整需要综合考虑网络规模、节点度数、链路容量、流量模式等多维特征。以下是具体的调整策略和实现方法：

1.8.2.1、基于网络规模的自适应策略

网络规模感知步长

核心思想：步长应与网络规模成反比，避免在大型网络中因步长过大导致震荡。

调整公式：

η0=∣V∣ηbase

其中：

ηbase：基础步长（通常0.1-1.0）
∣V∣：网络节点数

理论依据：次梯度法的收敛速度与∣V∣1相关，大网络需要更小的步长保证稳定性。

链路数量修正

修正因子：

ηlink=∣V∣∣E∣η0

其中∣E∣为链路数量，∣V∣∣E∣反映网络密度。密集网络需要更小的步长。

1.8.2.2、基于节点度数的局部调整

度数感知步长

核心思想：高度数节点（核心交换机）应使用较小步长，因为其链路价格变化影响范围大。

局部步长：

ηe=deg(v)η0

其中deg(v)为链路e端点的最大度数。

瓶颈链路识别

识别方法：

计算链路利用率：ue=Ce∑fp
高利用率链路（ue>0.8）使用更小步长：ηe=η0⋅(1−ue)

1.8.2.3、基于流量模式的自适应

梯度方差感知

核心思想：梯度方差大时减小步长，避免震荡。

方差估计：

σ2=T1t=1∑T∥g(t)−gˉ∥2

步长调整：

ηt=1+σ2η0

对偶间隙指导

调整策略：

对偶间隙大时增大步长加速收敛
对偶间隙小时减小步长提高精度

启发式规则：

ηt=⎩⎨⎧ηt−1⋅1.1ηt−1⋅0.9ηt−1if gap>0.1if gap<0.01otherwise

1.8.2.4、分布式环境下的协调机制

全局-局部步长协调

分层策略：

全局步长：ηglobal，由参数服务器维护
局部步长：ηlocal=ηglobal⋅wlocal
权重wlocal根据本地拓扑特征计算

异步步长同步

定期同步：

各节点定期向参数服务器报告本地步长和收敛状态
参数服务器计算全局平均步长并广播
同步周期：Tsync=O(log∣V∣)

自适应学习率算法

AdaGrad风格：

ηe,t=∑s=1tge,s2+ϵη0

Adam风格：

维护一阶矩mt和二阶矩vt
ηt=η0⋅vt+ϵmt

1.8.2.5、工程实现建议

监控指标

对偶间隙：∣f(x)−D(λ)∣
梯度范数：∥gt∥
目标函数变化：∣f(xt)−f(xt−1)∣
链路利用率方差：反映负载均衡程度

动态调整规则

def adjust_step_size(eta_prev, metrics):
# 基于对偶间隙调整
if metrics['dual_gap'] > 0.1:
return eta_prev * 1.2
elif metrics['dual_gap'] < 0.01:
return eta_prev * 0.8
# 基于梯度方差调整
elif metrics['grad_var'] > threshold:
return eta_prev / math.sqrt(1 + metrics['grad_var'])
else:
return eta_prev
参数边界保护

最小步长：ηmin=10−6，避免数值问题
最大步长：ηmax=1.0，避免震荡
预热阶段：前100次迭代使用固定步长，再开始自适应

1.8.2.6、性能评估

收敛性验证

监控对偶间隙随时间变化
验证是否满足理论收敛速度O(1/T)

稳定性测试

注入链路故障，观察步长调整响应
测试突发流量下的稳定性

对比实验

固定步长 vs 自适应步长
不同网络规模下的性能对比

通过上述自适应策略，可以在不同网络拓扑和流量模式下自动调整步长参数，在保证收敛性的同时提升优化效率。

1.8.3 自适应步长调整的监控告警机制

在实际部署中，自适应步长调整的监控告警机制 需要从多维度指标监控、异常检测算法、告警策略、自动恢复机制四个层面构建完整的闭环体系。

1.8.3.1、核心监控指标体系

收敛性指标

对偶间隙：∣f(x)−D(λ)∣，反映解的质量
目标函数变化率：∣f(xt)∣∣f(xt)−f(xt−1)∣，检测收敛停滞
梯度范数：∥gt∥，反映优化方向

步长健康度指标

步长震荡幅度：mean(ηt)max(ηt)−min(ηt)，检测步长不稳定
步长变化频率：单位时间内步长调整次数
步长边界触达：ηt接近ηmin或ηmax的次数

系统性能指标

迭代次数：累计迭代次数，检测收敛速度异常
计算时间：单次迭代平均耗时
内存使用：对偶变量存储开销

1.8.3.2、异常检测算法

基于统计的异常检测

移动平均控制图：

计算指标zt的移动平均值μt和标准差σt
告警条件：∣zt−μt∣>3σt

指数平滑：

μt=αzt+(1−α)μt−1

σt2=α(zt−μt)2+(1−α)σt−12

基于机器学习的异常检测

孤立森林：检测异常数据点

LSTM异常检测：基于时间序列预测异常

聚类分析：识别异常模式

规则引擎

def check_convergence_anomaly(metrics):
# 对偶间隙长期不下降
if metrics['dual_gap'] > 0.1 and metrics['iterations'] > 1000:
return "CONVERGENCE_STALLED"

复制代码

 # 步长持续震荡
 if metrics['step_oscillation'] > 0.5 and metrics['step_change_freq'] > 10:
     return "STEP_OSCILLATION"
 
 # 目标函数发散
 if metrics['obj_func'] > 1e6:
     return "DIVERGENCE"
 
 return "NORMAL"

1.8.3.3、告警策略设计

告警级别划分

级别	触发条件	处理方式
CRITICAL	对偶间隙发散、目标函数爆炸	立即停止算法，人工介入
WARNING	收敛停滞、步长震荡	自动调整参数，通知运维
INFO	收敛缓慢、步长边界触达	记录日志，观察

告警抑制机制

去抖动：连续多次触发才告警
静默期：告警后一段时间内不重复告警
依赖关系：避免级联告警

告警通知渠道

邮件/SMS：关键告警实时通知
钉钉/微信：日常告警推送
监控大屏：可视化展示
工单系统：自动创建处理工单

1.8.3.4、自动恢复机制

参数自动调整

步长重置：

复制代码

def auto_adjust_step(anomaly_type, current_eta):
    if anomaly_type == "STEP_OSCILLATION":
        # 步长震荡，减小步长
        return current_eta * 0.5
    elif anomaly_type == "CONVERGENCE_STALLED":
        # 收敛停滞，增大步长
        return current_eta * 1.5
    elif anomaly_type == "DIVERGENCE":
        # 发散，重置为初始值
        return eta_initial

检查点与回滚

定期保存状态：每100次迭代保存对偶变量和步长
异常回滚：检测到异常时回滚到最近正常状态
重试机制：回滚后使用调整后的参数重新计算

故障转移

主备切换：主节点异常时切换到备用节点
负载均衡：将计算任务分发到健康节点
服务降级：异常时使用简化算法保证基本功能

1.8.3.5、监控系统架构

数据采集层

Agent部署：在每个计算节点部署监控Agent
指标暴露：通过Prometheus、OpenTelemetry暴露指标
日志收集：使用ELK/EFK收集日志

数据处理层

时序数据库：Prometheus、InfluxDB存储历史数据
流处理：Flink、Spark Streaming实时处理
规则引擎：Drools、Esper执行检测规则

告警管理层

告警路由：根据告警级别路由到不同处理人
告警聚合：合并相似告警，避免告警风暴
告警升级：长时间未处理自动升级

可视化层

监控大屏：Grafana展示关键指标
趋势分析：展示历史收敛曲线
根因分析：关联分析异常原因

1.8.3.6、最佳实践建议

基线建立

冷启动阶段：前100次迭代不告警，建立基线
黄金指标：定义核心监控指标和阈值
压力测试：模拟异常场景验证告警有效性

容量规划

存储容量：历史数据保留7-30天
计算资源：预留20%资源应对突发流量
网络带宽：监控数据传输开销

演练与优化

定期演练：模拟故障场景，验证告警响应
告警优化：根据误报率调整阈值
性能优化：监控系统自身性能，避免影响业务

通过上述监控告警机制，可以及时发现并处理自适应步长调整中的异常情况，确保算法在复杂网络环境下稳定运行。

1.8.4 不同类型的收敛异常自动恢复策略

针对不同类型的收敛异常，需要采用差异化的自动恢复策略，以下是具体的应对方案：

一、震荡型异常恢复策略

步长调整策略

核心思路：步长过大导致在最优解附近震荡，需要减小步长提高稳定性。

具体措施：

步长衰减：ηt=ηt−1×0.5，快速降低步长
步长下界保护：设置ηmin=10−6，避免步长过小导致停滞
自适应调整：当连续3次迭代目标函数变化方向相反时，触发步长衰减

恢复条件：震荡幅度∣f(xt)∣∣f(xt)−f(xt−1)∣<10−4时，恢复步长增长

动量调整

动量清零：β=0，消除历史梯度积累的影响
动量衰减：β=β×0.9，逐步降低动量系数
动量重启：检测到震荡时，重新初始化动量项

梯度裁剪

梯度范数限制：∥gt∥←min(∥gt∥,clip_value)
clip_value：根据历史梯度统计动态调整，通常设置为梯度均值的2-3倍
自适应裁剪：当梯度范数超过历史均值的3倍时触发裁剪

二、停滞型异常恢复策略

步长增大策略

核心思路：步长过小导致收敛缓慢，需要增大步长加速收敛。

具体措施：

步长倍增：ηt=ηt−1×1.5，快速增大步长
步长上界保护：设置ηmax=1.0，避免步长过大导致震荡
自适应调整：当连续10次迭代目标函数变化率<10−6时，触发步长增大

恢复条件：目标函数开始下降且变化率>10−5时，保持当前步长

学习率预热

线性预热：前100次迭代逐步增大步长：ηt=ηfinal×100t
余弦退火：ηt=ηmin+21(ηmax−ηmin)(1+cos(Ttπ))
周期性重启：每T次迭代重置步长到初始值，跳出局部最优

梯度方向修正

梯度平滑：使用指数移动平均：mt=βmt−1+(1−β)gt
Nesterov动量：先看未来位置，再计算梯度：xt+1=xt+β(xt−xt−1)−ηtgt
二阶信息：使用拟牛顿法或共轭梯度法，修正梯度方向

三、发散型异常恢复策略

紧急恢复机制

核心思路：算法严重发散，需要立即停止并回滚到安全状态。

具体措施：

检查点回滚：回滚到最近保存的正常状态（每100次迭代保存一次）
步长重置：ηt=ηinitial，恢复到初始步长
参数重置：重新初始化对偶变量和动量项

触发条件：

目标函数值f(xt)>10×f(x0)
对偶间隙>100
梯度范数∥gt∥>106

问题诊断与修复

梯度检查：验证梯度计算是否正确
数值稳定性：检查是否存在数值溢出或下溢
约束违反：检查对偶变量是否满足非负约束
数据异常：检查输入数据是否存在异常值

降级策略

简化算法：切换到固定步长或简化版本
子问题求解：将大问题分解为小问题分别求解
提前终止：达到最大迭代次数或时间限制时终止

四、差异化策略对比

异常类型	核心问题	主要措施	辅助措施	恢复目标
震荡	步长过大	步长衰减、动量清零	梯度裁剪、自适应调整	稳定收敛
停滞	步长过小	步长增大、学习率预热	梯度平滑、周期性重启	加速收敛
发散	算法失效	检查点回滚、参数重置	问题诊断、降级策略	恢复运行

五、组合策略与优先级

异常检测优先级

处理顺序：

发散检测：最高优先级，立即处理
震荡检测：中等优先级，快速响应
停滞检测：低优先级，周期性检查
策略组合

震荡+停滞：先处理震荡（步长衰减），再处理停滞（步长增大）
发散+震荡：先回滚到安全状态，再调整步长
多重异常：按优先级顺序处理，记录异常链用于根因分析

策略参数调优

检测阈值：根据历史数据动态调整
恢复强度：根据异常严重程度调整恢复力度
冷却时间：避免频繁触发恢复机制

六、监控与反馈

性能指标监控

收敛速度：记录目标函数下降曲线
步长变化：监控步长调整历史
异常次数：统计各类异常发生频率

自适应调优

阈值自适应：根据历史异常数据调整检测阈值
策略效果评估：评估恢复策略的有效性
参数优化：基于历史数据优化策略参数

告警与通知

关键异常：发散异常立即告警并通知运维
一般异常：震荡和停滞异常记录日志并预警
趋势分析：定期分析异常趋势，提前预防

通过上述差异化的自动恢复策略，可以针对不同类型的收敛异常采取精准的应对措施，在保证算法稳定性的同时，提升收敛效率和鲁棒性。

1.9 逻辑域设计

1.9.1 逻辑域

在分布式系统，特别是超大规模智算集群的网络管理中，逻辑域的划分方式直接决定了域首脑节点的选举机制和容灾策略的设计。不同的划分原则源于不同的优化目标，进而带来了不同的复杂性与可靠性之间的权衡。

特性维度	基于物理拓扑划分	基于业务逻辑划分	基于动态路径划分
选举依据	硬件能力与位置：优先选择性能最强、层级最高（如核心交换机）或位置中心的节点。	业务优先级与资源需求：由调度器指定或根据任务优先级、资源配额动态选举。	网络状态与路径质量：综合评估节点间的实时延迟、带宽、丢包率等动态指标。
选举方式	静态或半静态：通常在系统初始化或扩容时确定，变更不频繁。	动态与集中式：常由集群调度器（如Slurm, Kubernetes）在作业启动时指定。	完全动态与分布式：基于实时网络测量数据，通过一致性哈希或权重计算动态产生。
故障检测重点	硬件链路与节点存活：快速检测物理链路中断、交换机宕机。	任务执行状态与进度：重点关注首脑节点上的任务进程是否存活、是否僵死。	路径质量波动与对称性：敏锐感知网络延迟突增、带宽下降、路径不对称等性能劣化。
典型容灾策略	快速硬件切换：启用备份端口或备份交换机，依赖物理冗余。	任务级恢复：在备用节点上重新调度并启动整个任务，可能涉及计算状态恢复。	路径级重路由与流量调度：快速将流量切换到预计算或实时发现的备用最优路径上。
核心挑战	避免"脑裂"，确保主备切换后状态一致性。	故障恢复时间长，业务中断影响大；状态恢复复杂。	感知的实时性与准确性；切换过程中的流量抖动控制。

物理拓扑划分：稳定为先

这种划分方式与网络硬件布局强绑定，例如将一个机架（Top of Rack）、一个Dragonfly拓扑中的组（Group）或一个POD（Point of Delivery）划分为一个逻辑域。

选举机制 ：域首脑的选举相对静态。通常，该域内层级最高、处理能力最强的网络设备 会被预先指定为首脑节点，例如机架顶部（ToR）交换机或组内的核心交换机。选举主要依据的是设备的固定属性，如物理端口数量、交换容量、在拓扑中的中心性等。一旦选定，除非设备故障或网络拓扩容，否则不会轻易变更。
容灾策略 ：容灾依赖于硬件冗余 。首脑节点通常会配置冷备或热备节点 。故障检测通过简单的心跳机制 （如BFD协议）在毫秒级内发现节点或链路故障。一旦主节点失联，备份节点会立即启动，并通常配合控制平面协议（如SDN控制器）下发新的流表，更新路由信息。其核心挑战在于防止"脑裂"（即多个节点同时认为自己是主节点），并通过分布式锁或协议（如Paxos、Raft）保证状态同步。

业务逻辑划分：灵活为要

这种划分是为了服务上层应用，例如将一个AI训练任务（万卡集群）或一个租户的所有资源划分为一个逻辑域，其边界可能跨多个物理机组。

选举机制 ：首脑节点的选举是动态且由软件定义 的。通常由集群的资源调度器（如Slurm, Kubernetes）根据业务策略来指定。选举依据包括计算节点的资源充裕度 （CPU/内存剩余）、任务优先级 ，甚至是为了优化通信而选择的拓扑中心点。在AI训练中，一个承担参数聚合任务的服务器可能会被指定为逻辑上的"主节点"。
容灾策略 ：容灾发生在任务层级 。故障检测不仅监控节点存活，更关注任务进程的健康状态 。一旦首脑节点故障，策略不是简单切换IP，而是由调度器重新选择一个健康的计算节点 ，并将整个任务（或受影响的子任务）重新调度到新节点上。这可能涉及到计算状态的恢复（从检查点重启），因此恢复时间相对较长，但更适用于复杂的应用逻辑。

动态路径划分：敏捷自适应

这种划分旨在优化网络流量，逻辑域会随着网络状态动态变化，例如将为一次All-Reduce操作构建的通信树或一个高质量的传输路径组视为一个临时逻辑域。

选举机制 ：选举是持续、完全动态 的。首脑节点（或路径的汇聚点）的选择基于实时的网络测量数据 。通过一致性哈希 算法，或综合评估到其他节点的延迟、带宽、丢包率等指标，选择一个"中心化"或"质量最优"的节点来承担流量中继或调度职责。在Dragonfly拓扑中，可能会选择一个能使组内通信最大化、组间通信最小化的节点作为临时首脑。
容灾策略 ：容灾体现在路径的快速切换 和流量调度 上。故障检测非常敏锐，能够感知到微秒级的延迟抖动或带宽下降。当首脑节点或主要路径质量劣化时，系统会快速切换到预先计算好的备用路径，或实时计算新的最优路径。这种策略高度依赖于端网协同 和SDN控制器的实时调度能力，目标是将业务流量的中断降至最低。

1.8.2 物理拓扑划分

在物理拓扑划分的网络中，通过算法客观地量化节点的"中心性"来选举主节点，是确保网络公平性和韧性的关键。其核心在于利用图论中的中心性指标作为客观、可量化的选举依据，完全避免主观指定。

以下是几种核心的度量方法和一个综合的选举框架。

关键的中心性度量指标

首先，我们需要一套客观的指标来衡量节点的"中心性"。

度中心性：衡量连接广度
- 定义：一个节点的度中心性是指与其直接相连的邻居节点数量。这反映了该节点直接的本地影响力。
- 在选举中的应用 ：度中心性高的节点，通常意味着它是一个本地网络的枢纽。在需要优先保证局部通信效率的场景下，这是一个简单而有效的指标。
中介中心性：衡量控制力
- 定义：衡量一个节点位于网络中其他节点对之间的最短路径上的频率。计算过程通常是：计算网络中所有节点对之间的最短路径；统计有多少条最短路径经过该节点；将此数量归一化处理。
- 在选举中的应用 ：高中介中心性的节点像是网络的"交通枢纽"，对信息流动拥有较强的控制能力。选择此类节点作为主节点，有助于优化全局通信路径和减少平均延迟。
紧密中心性：衡量传播效率
- 定义：表示一个节点到网络中所有其他节点的最短路径距离的平均值的倒数。计算步骤为：计算该节点到其他每个节点的最短距离；求这些距离的平均值；取该平均值的倒数。值越大，说明该节点能越快地到达网络中的其他部分。
- 在选举中的应用 ：高紧密中心性的节点意味着信息从它传播到全网的平均时间最短。选择它作为主节点，可以实现更快的指令下发或状态同步。
局部聚集系数：衡量邻域凝聚力
- 定义：衡量一个节点的邻居节点之间彼此连接的程度，即节点的邻域有多接近一个"小团体"。计算方法是：计算邻居节点之间实际存在的边数，除以邻居节点间可能存在的最大边数。
- 在选举中的应用 ：高聚集系数可能意味着该节点处于一个高度冗余和稳定的局部网络中。虽然不直接决定全局中心性，但可作为评估节点所处局部环境稳定性的辅助指标。

综合选举算法框架

需要一个框架来综合运用它们进行选举。

信息收集阶段：每个节点通过周期性的链路层发现协议（如LLDP）或由控制平面（如SDN控制器）分发，获取全局网络拓扑图。
中心性计算阶段 ：每个节点（或集中式控制器）根据获取的拓扑图，独立计算网络中所有节点（包括自身）的上述各项中心性指标。
综合评分与排序阶段 ：这是避免主观性的关键。可以设计一个加权综合评分公式来融合不同维度的中心性。例如：

综合得分 = W₁ * 归一化度中心性 + W₂ * 归一化中介中心性 + W³ * 归一化紧密中心性

其中，W₁, W₂, W₃是根据网络业务特点设定的权重。例如，若网络更关注全局数据传输效率，可赋予中介中心性更高权重。之后，所有节点按综合得分排序；得分最高者当选。若出现平分，可使用节点ID或硬件地址等不可变且唯一的标识符作为决胜规则。
选举与容灾阶段 ：可采用类似Raft算法的心跳机制。主节点定期向从节点发送心跳。若从节点超时未收到心跳，则触发新一轮的中心性计算和选举流程，实现快速故障恢复。

设计考量与权重分配

在实际设计中，还需考虑一些关键因素。

权重分配策略 ：权重的设定本身应基于网络策略，而非主观偏好。例如，为一个数据采集网络 （如传感器网络）设计选举算法时，可能更看重度中心性 ，因为主节点需要直接连接尽可能多的传感器。而在一个通信骨干网 中，中介中心性 和紧密中心性可能更为重要，以保障任意两点间的通信效率。
动态调整与更新 ：网络拓扑并非一成不变。选举算法需要能应对变化，例如设置定期重选机制 或在检测到拓扑发生显著变化（如重要节点或链路故障）时主动触发重选举。
与现有协议结合 ：此框架可与成熟的一致性算法（如Raft）结合。例如，在Raft的选举阶段，不是完全随机地设定选举超时时间，而是可以让中心性评分更高的节点拥有更短的超时时间，从而使其能更快地发起投票请求，增加当选概率，这既利用了中心性信息，又保持了算法的稳健性。

1.8.3 计算中介中心性

在实际的网络分析与部署中，计算中介中心性等指标确实面临着计算复杂度的挑战，但业界也发展出了多种有效的优化策略来应对大规模网络。

理解核心算法复杂度

中介中心性衡量的是一个节点在所有节点对最短路径上出现的频率。最直接的算法是计算所有节点对之间的最短路径，然后统计每个节点被经过的次数。这种"暴力"方法的时间复杂度高达 O(|V|³)（|V|代表节点数），对于大规模网络几乎不可行。

目前公认更高效的精确计算算法是 Brandes算法 ，它将复杂度降低到了 O(|V| |E|)，其中 |E| 是边的数量。这对于许多实际网络（尤其是稀疏网络）来说快了很多。不过，当网络规模极大（节点和边数达到百万甚至千万级别）时，即使是 O(|V| |E|) 的复杂度在单台计算机上也可能需要很长的计算时间或超过内存限制。

应对大规模网络的优化策略

为了应对超大规模网络的计算挑战，研究人员提出了多种优化方案，下表对比了其主要思路和特点：

策略方向	核心思路	优点	缺点/考虑
近似算法	通过随机采样部分节点作为源点来计算最短路径，估算全局中心性。	显著提速，有时在采样1%-5%节点后就能获得不错的近似结果。	结果存在误差，需在精度和效率间权衡。
分布式计算	利用Spark、GraphX等框架将图数据和计算任务分布到多台机器并行处理。	能处理单机无法容纳的巨图，充分利用多机资源。	有通信开销，系统复杂度高。
利用图拓扑特性	根据实际网络（如社交、交通网）的模块化（社区结构）等特性简化计算。	针对特定网络类型可能非常高效。	通用性可能受限，依赖于网络结构。
机器学习模型	训练图神经网络（GNN）等模型，学习节点的拓扑特征，从而预测其中心性排名。	一旦模型训练好，预测速度极快，适合动态变化网络。	需要大量数据训练，且预测准确性是关键。
改进的精确算法	针对特定图结构（如超大型平面图）设计更优的精确算法。	在特定条件下可处理更大规模的图。	适用范围可能有局限。

除了上述策略，还有一些结合多种思想的混合方法。例如，有专利方案提出先计算特征向量中心性（一种计算成本相对较低的指标）来识别网络中的"重要"节点，然后以这些重要节点为主要样本进行中介中心性的近似计算，从而在保证代表性的同时进一步提高效率。

如何选择合适的方法

选择哪种优化策略，取决于你的具体需求：

追求极致精度且网络规模可控：Brandes算法或其分布式实现（如基于Spark GraphX）是可靠选择。
处理海量数据，允许一定误差 ：优先考虑近似算法 （如基于随机采样）或分布式计算框架。
网络动态变化，需快速评估 ：可以探索机器学习方法，虽然仍处于前沿研究阶段，但潜力巨大。

1.8.4 解决网络分区导致的"脑裂"问题以及根据网络拓扑优化领导者选举

在分布式系统，特别是超大规模智算中心的网络设计中，解决网络分区导致的"脑裂"问题以及根据网络拓扑优化领导者选举，是确保系统高可用和高性能的核心。

防止脑裂：分布式一致性的基石

"脑裂"是指在网络分区时，集群中可能同时出现多个主节点，导致数据不一致。成熟的一致性协议通过严谨的机制从根本上防止这一问题。

Raft协议的安全机制

Raft协议通过组合多种机制来确保安全性：
1. 任期机制 ：每个选举周期都有一个唯一且递增的任期号。任何通信都携带任期号，节点无条件认同更高的任期，这有效识别并拒绝了过时的主节点。
2. 多数派原则 ：一个节点必须获得超过半数 的投票才能当选为主节点。此规则的精妙之处在于，即使发生网络分区，也最多只能有一个分区包含多数节点并成功选举。少数派分区由于无法获得多数票，根本无法产生有效的主节点，从而自然避免了脑裂。
3. 日志完整性约束：在选举投票时，节点会优先投票给日志序列号更高、数据更完整的候选者，这保证了新主节点拥有最全的数据，避免数据回退。
ZooKeeper的ZAB协议

ZAB协议与Raft思想类似，同样依赖过半选举来确保唯一主节点。其核心在于，只有当主节点的提案被超过半数的从节点确认后，才会被提交。这意味着，在网络分区场景下，仅有多数派分区的主节点能成功提交数据，少数派分区的主节点写入无效，从而保障了数据一致性。

拓扑感知的选举优化策略

在确保不会发生脑裂的安全基础上，我们可以根据不同网络拓扑的特性，优化选举策略，以提升系统性能。

Fat-Tree / Clos网络

这类网络高度对称，任意两点间存在多条等价路径。领导者选举的首要目标是避免将主节点放置在可能成为瓶颈的位置。
- 优化思路 ：应避免将主节点过度集中在某一台核心交换机上。可以利用中介中心性 来识别网络中承载最多流量的关键节点，但考虑让其承担路由中枢的角色，而非一定作为主节点。选举时，可适当降低此类节点的选举权重，或结合度中心性，选择与更多节点有直接高速连接的设备（如某一汇聚层交换机），以保证主节点与多数工作节点有优异的网络性能。
Torus网络

在2D/3D-Torus这种规则网格中，通信延迟与节点间的曼哈顿距离紧密相关。
- 优化思路 ：领导者选举应优先考虑紧密中心性最高的节点。这样的节点到网络中所有其他节点的平均距离最短，由其作为主节点可以有效降低集群内部的平均通信延迟。对于需要频繁进行全局操作（如All-Reduce）的业务，这一点尤为重要。
Dragonfly网络

Dragonfly拓扑具有鲜明的层次结构（组内全连接，组间稀疏连接），其选举策略最为复杂，需要权衡全局通信效率和局部通信效率。
- 优化思路：
  1. 全局视角 ：若业务涉及大量跨组通信，主节点应优先部署在组间连接的核心枢纽 上。可以通过计算全局的中介中心性来识别这些关键节点。
  2. 局部视角 ：若业务主要在组内进行，可考虑采用分域选举策略。即在每个组内选举一个本地协调者，再由这些协调者进行全局决策。这能显著减少跨组的管理流量。
  3. 动态调整 ：在Dragonfly网络中，没有一成不变的最优解。最理想的策略是让选举算法能够感知业务的通信模式，并动态调整权重。例如，当系统检测到All-to-All通信模式占主导时，应提升全局中心性指标的权重。

总结与实施路径

总而言之，构建稳健高效的分布式系统需要分层施策：

安全基石 ：首先，必须依赖Raft 或Paxos 等成熟的一致性协议，利用其多数派原则 和任期机制，从协议层面根除脑裂的可能性。
性能优化 ：在此基础上，根据具体的网络拓扑（如Fat-Tree, Torus, Dragonfly）特性，将紧密中心性、中介中心性等图论指标融入选举策略。其目标是在保证安全的前提下，让主节点出现在网络拓扑的"最佳位置"，从而最小化通信延迟、最大化系统吞吐量。

1.8.5 随机采样近似算法的误差分析

梳理了误差理论分析和不同采样策略影响的核心框架：

核心维度	关键问题	核心方法与工具
理论误差边界	采样估计值 & 真实值之间的最大可能差异是多少？	概率不等式（如切比雪夫不等式、霍夫丁不等式）、大数定律
采样策略的影响	不同的"取样"方式，如何影响最终估计的精度？	比较不同策略（如简单随机采样、分层采样、自适应采样）的方差与偏差

误差边界的理论分析框架

理论分析的核心目的是为采样估计的误差提供一个概率意义上的上界，即回答"估计值偏离真实值超过某个范围的概率有多大"这个问题。

概率不等式的角色

最经典的工具是切比雪夫不等式 。它提供了一个非常通用的边界：对于任何具有有限方差 σ² 的随机变量，其估计值偏离期望值超过 t 个标准差的概率至多是 1/t² 。这意味着，方差越小，达到相同精度要求的所需样本量就越小。

当采样过程满足某些更严格的条件时，霍夫丁不等式 能提供更紧（更精确）的误差边界。它要求观测值独立且有界。霍夫丁不等式指出，误差超出特定范围的概率随样本量增加呈指数级下降，这比切比雪夫不等式给出的多项式衰减（1/t²）要快得多，解释了为什么在某些情况下采样算法能非常高效。
大数定律：稳定性的保证

大数定律 是采样近似之所以可行的基石。它告诉我们，随着样本数量 n 的不断增加，样本的平均值会几乎必然地收敛于期望值（真实值）。理论误差分析在很大程度上就是量化这个收敛速度有多快。

采样策略如何影响精度

不同的采样策略通过改变估计量的方差和偏差来影响最终精度。

简单随机采样

这是最基础的策略。虽然通常无偏，但其方差可能较大，精度主要依赖样本数量。若要提高精度，就需要显著增加样本量 n 。
更智能的策略：减小方差与适应结构
- 分层采样 ：当对总体结构有一定先验知识时（如知道数据可分为几个内部差异较小的层），采用分层采样是高效的选择。它通过确保每层都有代表性样本，显著减小估计量的方差，从而在相同样本量下获得更高精度，或者在相同精度要求下减少样本量。
- 自适应采样与考虑数据相关性 ：对于复杂问题，更高级的策略能动态调整采样过程。例如，在构建数据库直方图时，考虑数据页面内部元组的相关性（如是否有序存储）的自适应采样算法，能够更智能地决定采样量，避免过度采样，提升效率。
- 处理噪声与离群点 ：当数据中含有大量噪声或离群点时，RANSAC 等策略通过随机抽取最小子集拟合模型，并选择具有最多"共识"数据点的模型，特别适用于这种情况，其精度和鲁棒性远超直接使用所有数据（包括噪声点）进行拟合的方法。
策略选择对特定度量的影响

有研究专门模拟了不同类型采样偏差对网络节点中心性等度量的影响。结果表明，局部中心性度量通常比全局度量对采样偏差更具鲁棒性。这意味着，选择采样策略时，需要考虑你所关心的指标特性。

其他影响因素与平衡之道

误差来源分解 ：总误差可分解为抽样误差 （由于随机性导致）和非抽样误差（如测量误差、模型设定误差等）。理论分析主要针对抽样误差，但实践中需意识到非抽样误差的存在。
偏差-方差权衡 ：某些更复杂的采样策略可能引入微小偏差以极大降低方差，从而在均方误差意义下获得更优的整体估计效果。这是一个重要的权衡思路。
利用问题本身结构 ：在特定应用中，利用已知的问题结构可以设计更有效的策略。例如，在参数估计中，无迹变换 采用确定性采样点来精确捕捉参数分布的均值和方差信息，这种策略优于纯随机采样。

总结与建议

面对实际问题时，建议遵循以下思路：

明确需求 ：首先确定你对估计结果的精度要求 （可接受的最大误差）和置信度要求。
分析数据：评估数据的特性（分布、噪声水平、结构性等）。
选择策略：根据需求和数据特性，参考上述分析选择最合适的采样策略。
理论估算：利用概率不等式初步估算所需样本量，作为起点。
迭代验证：在可能的情况下，通过模拟或小规模实验验证理论估计，并据此调整策略和样本量。

1.8.6 网络分区场景下确保分布式系统的行为可控和数据一致

在网络分区场景下，确保分布式系统的行为可控和数据一致是核心挑战。下面这张时序图直观地展示了少数派分区主节点从网络隔离到最终恢复的完整生命周期和关键交互。

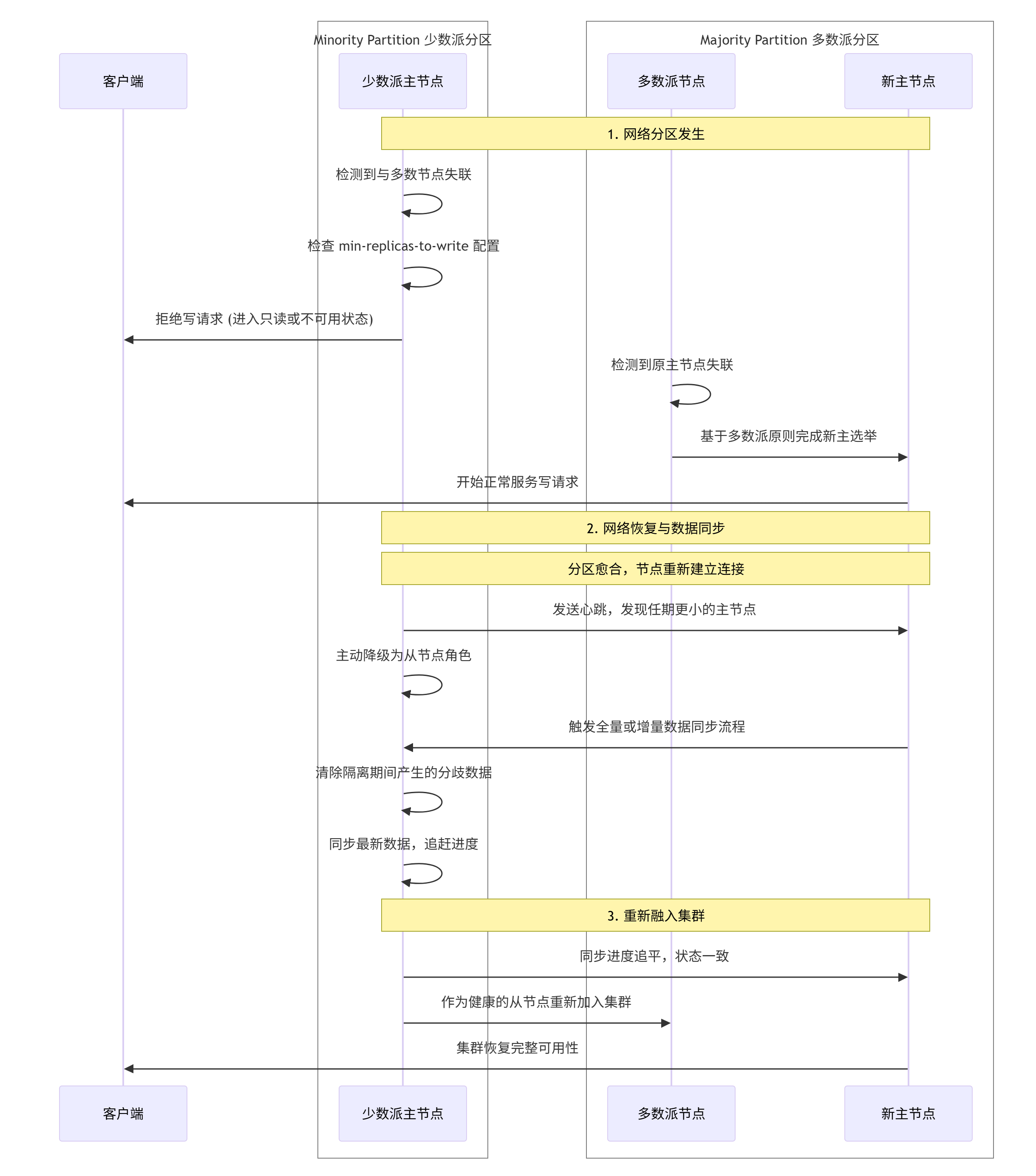
上图概括了少数派主节点从隔离到恢复的关键阶段。下面我们深入每个阶段，结合不同系统的具体策略（如 Redis Cluster、OceanBase、RabbitMQ）来看其中的细节和设计考量。

少数派分区的行为与限制

网络分区发生后，处于少数派分区的主节点会快速进入一种自我保护状态 。其核心目标是防止在隔离期间产生无法调和的数据分歧，即避免"脑裂"。

进入只读或不可用状态 ：以 Redis Cluster 为例，如果配置了 min-replicas-to-write（旧版叫 min-slaves-to-write），当主节点发现其存活从节点数量低于此阈值时，会停止处理所有写请求 。它可能会返回错误或直接拒绝，从而确保在数据同步链不完整的情况下，不会接受任何可能导致数据不一致的新写入。RabbitMQ 的默认 pause-minority模式策略更为彻底，处于少数派的节点会直接暂停整个服务进程 （进入 partitioned状态），不提供任何读写服务，从根本上杜绝了数据分歧的产生。
心跳检测与故障认定 ：集群中的节点通过心跳机制（如 Gossip 协议）来感知彼此的状态。当多数派分区的节点在 node-timeout内无法与少数派的主节点通信时，他们会通过投票将其标记为失效（FAIL），并触发新的主节点选举。此时，集群的"大脑"已经转移到了多数派分区的新主节点上。

数据同步与恢复流程

当网络分区愈合，关键的恢复流程开始运作。此阶段的目标是安全、高效地将少数派节点重新纳入集群，并确保数据最终一致。

发现与降级 ：网络恢复后，原少数派主节点重新与其他节点建立连接。当它发出心跳或接收响应时，会发现自己持有的"任期"（Term）或"纪元"（Epoch）已经落后于当前集群中的新主节点 。根据分布式共识算法（如Raft），它会立即承认新主节点的领导地位，并自动降级为从节点（Follower/Replica）。
数据同步决策：新主节点会根据原主节点落后的程度决定同步策略。
- 增量同步：如果原主节点隔离时间较短，其数据差异不大，新主节点只需将隔离期间缺失的增量日志（在Redis中可以是AOF日志，在OceanBase中是Clog）发送给它，使其快速追平。
- 全量同步 ：如果原主节点隔离时间过长，其数据过于陈旧，或者与现有数据存在根本性冲突，新主节点会触发全量同步。这将是一个更耗时的过程，新主节点会生成当前数据的快照（如Redis的RDB文件）发送给原主节点，使其数据完全被覆盖。OceanBase 的 Clog 同步机制也描述了类似逻辑，Follower副本会主动从Leader副本拉取缺失的日志或直接重建基线数据。
分歧数据处理与冲突解决：这是最关键的环节。对于在隔离期间被少数派主节点接受的写入（如果其处于只读模式则无此问题），处理方式取决于系统的一致性模型。
- 强一致性系统 ：如 OceanBase ，基于Paxos协议，要求日志在多数派持久化才算提交成功。因此，少数派主节点在隔离期间接受的、未得到多数派确认的写入会被视为无效，在恢复时会被直接丢弃。系统会保留多数派分区上已达成共识的数据。
- 最终一致性系统：这类系统可能会尝试自动解决冲突（如基于时间戳或版本号），但也可能将冲突暴露给应用层，由业务逻辑决定如何解决（例如，提示用户数据冲突，由用户手动选择保留哪个版本）。

设计权衡与最佳实践

不同的恢复策略反映了系统在一致性（C） 、可用性（A） 和**分区容错性（P）** 之间的权衡。

CP系统优先保证一致性 ：如配置了 pause-minority的 RabbitMQ 或强同步的数据库，在网络分区时宁愿让少数派分区完全不可用，也要保证数据不出错。这适合对数据一致性要求极高的金融、交易场景。
AP系统优先保证可用性：如一些默认配置下的 Redis Cluster，在分区时可能允许少数派主节点继续服务，但需承担后续数据冲突解决的成本。这适合可接受短暂数据不一致的互联网应用。

最佳实践建议：

合理配置 ：根据业务需求，设置 min-replicas-to-write等参数，在可用性和一致性之间找到平衡点。
监控报警：建立完善的监控体系，对网络分区和脑裂风险进行实时告警。
客户端容错：设计智能的客户端，能够感知集群状态变化，在主节点失效时自动重定向到新的健康节点。

1.8.7 网络分区后进行数据同步时处理少数派分区的数据冲突

在网络分区后进行数据同步时，处理少数派分区的数据冲突确实是个关键挑战。其核心思路是先精确识别冲突，再根据业务场景选择合适的策略自动或手动解决。

主流的冲突解决算法:

算法分类	核心原理	典型应用场景	优势	劣势
简单规则类	依据单一、明确的规则（如时间戳、序列号）决定胜出者。	配置数据、缓存覆盖、不重要的元数据。	实现简单，性能开销低，能快速达成一致。	可能造成数据丢失（如LWW），规则本身可能不公。
自动合并类 (CRDT)	基于数学定义的数据结构，确保并发操作可交换、结合、幂等，自动收敛。	分布式计数器、协同编辑、购物车、点赞数。	无需协调，高可用性低延迟，自动解决冲突。	数据结构有限制，实现复杂，存储开销可能较大。
操作转换类 (OT)	对操作本身进行转换重排，使得在任意顺序下都能得到相同结果。	实时协作编辑（如Google Docs）。	适合复杂操作，保留操作意图。	中心式协调较常见，算法复杂度高。
可定制策略类	提供框架，允许业务自定义合并逻辑（如合并字段、提示用户）。	用户资料、订单状态、复杂的业务对象。	灵活，能适应特定业务需求，平衡自动与人工。	实现复杂度高，可能需要业务逻辑深度介入。

如何识别数据冲突

在解决冲突之前，系统必须能准确地发现它们。这主要依赖于版本控制技术，就像一个精密的"数据指纹"系统。

版本向量 (Version Vectors) / 向量时钟 (Vector Clocks) ：这是追踪数据变更起源的利器。它为每个数据副本维护一个向量，记录来自不同节点（或设备）的更新次数。同步时，通过比较两个向量的先后关系，可以精确判断出数据是先后继发 （有明确的先后顺序），还是并发冲突（需要解决）。
哈希/内容指纹 (Hash/Content Fingerprinting)：对于不确定数据是否已变更的场景，可以计算数据内容的哈希值（如MD5）。如果两个副本的哈希值不同，则说明内容肯定发生了冲突。
Merkle 树 (Merkle Trees)：当需要快速比较大量数据（如整个数据库）的差异时，Merkle树结构可以高效地定位到具体是哪一部分数据存在不一致，从而避免全量对比。

主流冲突解决算法详解

识别出冲突后，便可根据业务需求选择合适的算法进行解决。

1. 简单规则策略

这类策略逻辑简单，决策快速，适用于对数据一致性要求不极致的场景。

LWW (Last Write Wins)：让最后时间戳的写入操作获胜。这是最简单的策略，但风险在于"最后"依赖于各节点时钟，若时钟不同步，可能导致数据意外丢失。
节点优先级 (Node Priority)：预先给节点（如主数据中心）分配更高优先级，其写入总是优先。

2. 自动合并策略

这类策略旨在实现"无冲突"的复制数据类型，适合需要高可用和低延迟的场景。

CRDT (Conflict-free Replicated Data Types)：CRDT设计了一套数学上就能保证最终一致性的数据结构。例如，对于一个分布式计数器，无论加减操作的顺序如何，最终所有副本都能收敛到正确的总和。
操作转换 (Operational Transformation, OT)：OT通过调整操作顺序来解决冲突。在协同编辑中，当两个用户同时在不同位置插入字符，OT算法会转换这些操作的位置参数，使得最终文档状态一致。

3. 可定制与混合策略

对于复杂的业务逻辑，往往需要更灵活的、定制化的解决方案。

业务规则合并 (Business Rule Merging)：根据预定义的业务规则进行合并。例如，合并用户资料时，可以设定规则合并"昵称"和"地址"字段，但以最后一次更新为准覆盖"手机号"字段。
人工干预 (Manual Intervention) / 冲突提示：当系统无法自动解决时（如两个用户同时修改了合同的重要条款），会将冲突标记出来，通知相关方（如用户或管理员）进行手动裁决。在某些系统中，也会在自动解决后保留冲突版本的历史记录，以备审计或恢复之需。

选择与实施建议

在实际工程中，选择哪种策略往往需要权衡：

业务需求是根本：先问"这个数据有多重要？"对于购物车商品数量，CRDT可能是最佳选择；对于银行账户余额，则可能需要更谨慎的策略。
考虑用户体验：自动合并对用户无感，体验顺畅；但某些关键场景，适时提示用户决策可能更合理。
架构复杂度：LWW实现简单，而CRDT和OT则需要更深入的架构设计。
组合使用：一个系统内通常不会只采用一种策略。可以对不同的数据模型或操作类型采用不同的冲突解决算法。

1.8.8 基于动态路径划分逻辑域的数据中心网络容灾方案

动态路径划分逻辑域的核心思想

传统的网络容灾往往依赖于静态的、预先规划好的备份路径或固定拓扑（如Fat-Tree、Clos）。而"动态路径划分逻辑域"的策略，其核心在于 "感知状态，动态重组"。

从"静态固定"到"动态逻辑域" ：它不再将网络视为一个僵化的物理连接集合，而是通过SDN（软件定义网络）、NFV（网络功能虚拟化）和智能控制平面，根据实时的网络状态（如链路延迟、丢包率、带宽利用率） 和业务需求（如SLA要求、通信模式），动态地将物理网络资源划分成多个虚拟的"逻辑域"。这类似于在庞大的物理网络上，按需"画"出若干条最优或备用的高速公路网。
路径划分的驱动因素：划分的依据是动态的。例如，当监控系统检测到某条链路延迟急剧升高或即将发生拥塞时，控制平面可以迅速计算并启用一条绕过该区域的新路径，从而形成一个临时的、更优的逻辑通信域。

业务与网络系统的容灾实现

在这种动态网络的基础上，容灾的实现变得更加智能和自动化。

业务系统容灾：基于逻辑域的快速切换

对于业务系统而言，这种架构的容灾体验是"无缝"或"平滑"的。当动态路径划分机制感知到故障或性能劣化时，控制平面会自动将业务流量调度到预设的、健康的逻辑域中的路径上。对于需要维持状态的业务（如数据库会话），需要结合应用层的能力（例如，通过分布式会话存储将状态与具体服务器解耦）来实现真正的无感知切换。
网络系统自身容灾：动态控制平面

网络系统的自愈能力是关键。控制平面会持续监控底层物理设备与链路。一旦发现故障（如链路中断、交换机宕机），它会重新计算全网的可达性，并动态调整逻辑域的划分边界和路径策略，确保网络本身在部分组件失效后仍能保持连通性和服务能力。这依赖于控制平面集群的高可用性设计（如基于Raft协议选主）和东西向通信的可靠性。

图论与复形几何的深度应用

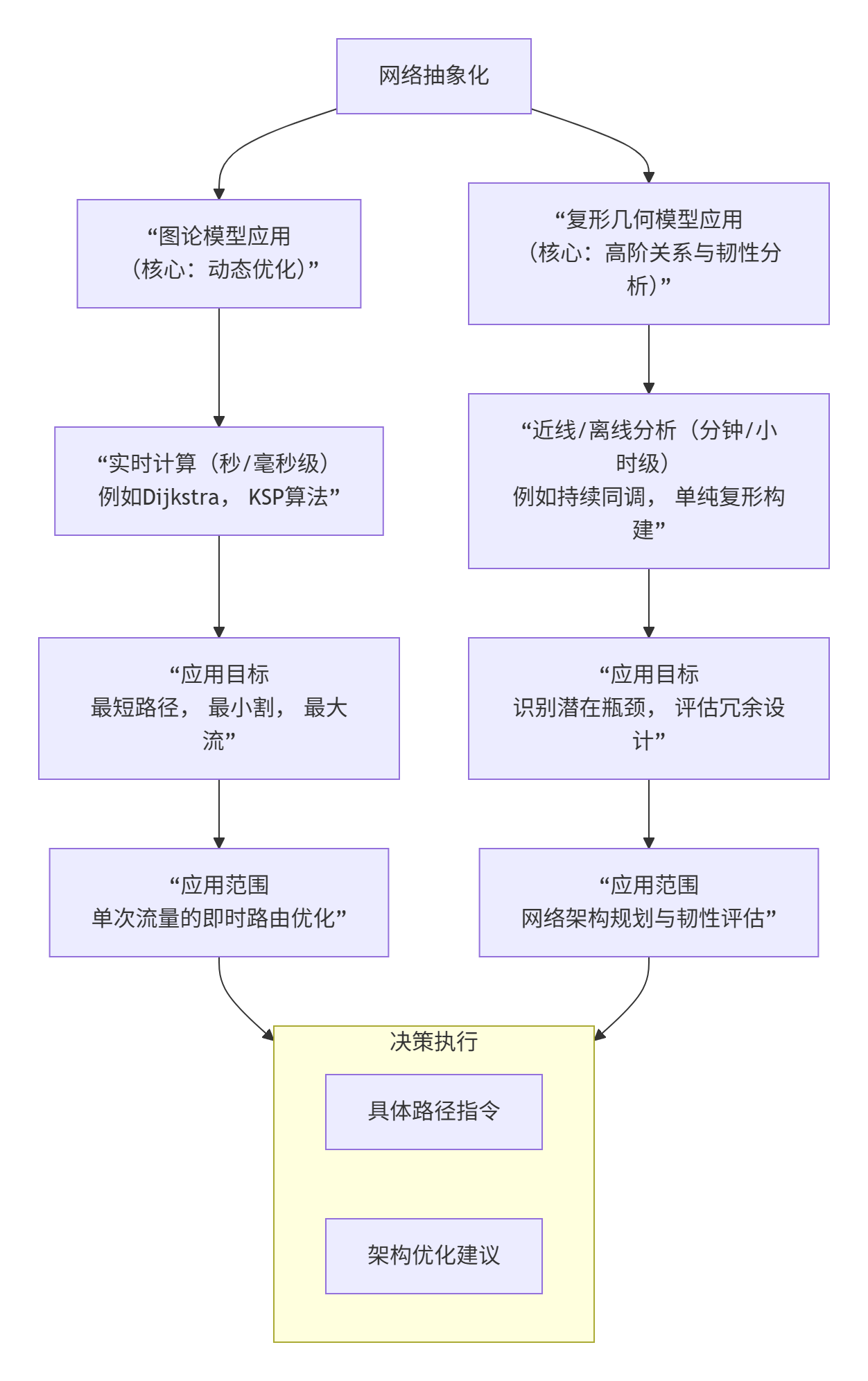
如上图所示，图论和复形几何在网络认知和决策中扮演着不同但互补的角色。

图论模型的应用 主要聚焦于动态优化 ，处理的是网络中的成对连接关系（即边）。它的应用通常是实时或近实时的，目标是解决具体的路由问题，例如为单个数据流或故障切换场景快速计算最优路径。
复形几何模型的应用 则侧重于高阶关系与韧性分析 ，处理的是多个网络元素之间复杂的群体依赖关系（如共享同一底层资源的多条链路）。它的分析过程计算量更大，通常用于近线或离线的网络架构规划与全局韧性评估。

通过这种分工协作，网络管理系统能够在不同时间尺度和抽象层次上做出智能决策，从而实现对动态路径划分逻辑域的有效支撑。

1.8.9 图论中的最大流-最小割定理支持网络容灾设计

在动态路径划分网络中是如何具体助力容灾路径计算：

理解最大流与最小割

要理解容灾路径计算，首先要掌握两个基本概念：

最大流问题 ：想象网络是一个管道系统，水从源点（比如水泵s）流向汇点（比如水池t），每条管道都有其最大流量（容量）。最大流算法（如 Ford-Fulkerson算法 、Dinic算法 ）就是计算在不超过所有管道容量的前提下，单位时间内能从s到t的最大水流量。这个过程通常通过不断在残量网络 中寻找增广路径来实现。
最小割问题 ：一个割将网络节点划分为包含源点s的集合S和包含汇点t的集合T。割的容量 是所有从S指向T的边的容量之和。最小割 就是所有可能的割中，容量最小的那个。最大流-最小割定理指出：任何一个网络中，从源点到汇点的最大流量值等于最小割的容量 。最小割揭示了网络的瓶颈或最薄弱环节，一旦最小割中的边全部失效，s和t之间的通信就会完全中断。

最小割与最大流在容灾路径计算中的角色

在动态路径划分网络中，容灾路径计算的目标是找到一条或多条与主路径风险分离的备份路径。最大流和最小割算法在此过程中扮演不同但协同的角色：

评估路径冗余性 ：计算源节点到目的节点的最大流值。如果最大流值大于当前主路径所需带宽，说明网络存在天然的路径冗余，具备构建备份路径的基础。
识别关键风险区域 ：最小割集直观地标定了网络中连接源和目的节点的最关键链路集合 。在容灾规划中，核心原则之一就是确保主备路径不同时经过最小割集中的边，从而避免单点故障导致业务中断。
指导风险分离路径计算 ：高级的容灾方案要求路径间实现风险分离 。例如，一种方法会先计算出一条主路径（AP），然后在网络拓扑中移除所有与主路径边共享风险的链路，构成一个删减图（Go）。接着，在这个删减图上尝试计算备份路径（BP）。若计算失败，则可能利用最大流最小割算法进一步分析冲突，将问题分解为子问题并行求解。

动态路径划分网络的特殊考量

动态路径划分网络（如SDN驱动的网络）的特点是网络控制和路径分配更加灵活。这使得容灾路径计算可以实现动态优化：

动态风险感知 ：网络控制器可以实时或近实时地收集网络状态（如链路利用率、延迟、丢包率）。结合最大流和最小割分析，可以动态调整逻辑拓扑的划分，主动规避已出现拥塞或潜在故障的区域。
多路径负载均衡与容灾结合 ：通过最大流算法可以计算出多条可行路径及其可用带宽。这不仅可用于容灾切换，还能在正常运行时进行负载均衡，将业务流量动态分配到多条路径上，提升整体资源利用率和性能。当某条路径故障时，流量可以快速切换到其他预计算好的路径上。
智能化路径选择 ：前沿研究开始探索将**图神经网络（GNN）** 与最大流-最小割分析相结合。GNN能有效学习复杂网络拓扑的结构特征，从而更精准地预测路径可靠性，辅助选择最优的容灾路径。

核心价值总结

总而言之，最大流和最小割算法为动态路径划分网络的容灾设计提供了量化的分析工具 和清晰的优化方向。它们帮助网络规划者：

精准定位网络中最脆弱的环节（最小割）。
科学评估网络的冗余能力和潜在备份路径（最大流）。
动态指导风险分离的容灾路径计算，确保业务的高可用性。

1.8.10 动态路径划分控制平面平衡实时计算开销与容灾响应速度

在实际工程中，动态路径划分控制平面平衡实时计算开销与容灾响应速度，确实是一个核心挑战。这需要一套精细的策略，而非单一的技术方案。其核心思想是：通过分层处理、智能调度和算法优化，将有限的计算资源"好钢用在刀刃上"。

核心平衡策略

为了让你快速把握全局，下表梳理了关键的平衡策略及其背后的逻辑：

平衡维度	核心策略	如何实现平衡？
计算架构	分层处理与任务卸载	将计算任务分为轻重缓急。简单、局部的决策（如单个链路故障切换）在网络设备本地或近端快速执行；复杂、全局的路径重规划由中心控制器周期性或触发式进行。
数据调度	增量更新与预测预计算	并非所有数据都需要全量实时同步。控制平面只关注发生变化的路段状态（增量更新）。同时，基于历史数据和趋势，提前预测可能发生的故障场景并预计算备用路径，变实时计算为"闪电式"调用。
算法选择	优化求解效率	采用计算效率更高的算法。例如，在应急路径规划中，改进的涟漪扩散算法（RSA）相比传统遗传算法（如NSGA-II），能在保证解的质量的同时，显著缩短计算时间，从而更快地提供多种可靠路径方案。
响应机制	分级容灾与快速重路由	并非所有故障都需要启动复杂的全局重规划。对于单点链路或节点故障，利用预先部署的快速重路由（FRR）技术，在毫秒级内将流量切换到本地备份路径上。这为控制平面进行更优的全局调整赢得了宝贵时间。

策略的协同运作

上述策略在实际系统中是协同工作的，形成一个高效的闭环：

常态下的预演与准备 ：控制平面会利用相对空闲的周期，基于网络拓扑和流量模型，模拟计算各种可能的故障场景下的最优逃生路径，并将这些路径作为"预案"下发到相关网络设备。这个过程就像进行消防演练，虽然耗费一些计算资源，但为紧急情况下的快速响应做好了准备。
故障瞬间的快速止血 ：当故障真的发生时，系统首先会启动最快的本地响应机制。例如，在数据中心网络中，设备会通过**快速检测机制（如BFD）** 感知到相邻链路中断，并立即执行预配置的快速重路由（FRR），在几十毫秒内完成流量切换，优先保证业务不中断。这个阶段追求的是速度，可能牺牲了路径的最优性。
故障后的全局优化 ：在业务流量得到初步恢复后，控制平面会收集全网最新的状态信息。它可能利用增量计算算法，只在故障影响的局部区域进行路径重优化，而不是对整个网络进行全量计算，从而以较小的开销计算出更优的全局路径。之后，它会将优化后的路径策略平滑地更新到网络中，替换掉临时性的FRR路径，实现网络性能的恢复和提升。

1.8.11 Dinic算法在动态网络容灾计算中的优势

Dinic算法在动态网络容灾计算中，相比基础的Ford-Fulkerson算法，确实展现出了多方面的性能优势。这些优势主要源于其更智能的搜索策略和更高效的计算模式。

特性维度	Ford-Fulkerson算法	Dinic算法	对动态网络容灾计算的意义
核心搜索策略	单纯依赖深度优先搜索（DFS）随机寻找增广路径。	采用BFS构建分层网络 + DFS进行多路增广的组合策略。	极大减少了寻找增广路径的盲目性，系统性地探索网络，避免绕远路。
时间复杂度	理论上界为 *O(E \|f\|)**，其中\|f\|为最大流值，对于容量大的网络可能很差。	理论复杂度为 O(V²E) ，是强多项式时间算法，与边容量大小无关。	在大型网络或高容量链路场景下，计算时间可预测且稳定，满足容灾调度的实时性要求。
容灾计算效率	每次只能找到一条增广路径，效率较低，尤其对网络结构变化响应慢。	每轮BFS构建分层图后，可在该图上进行多路DFS增广，充分利用已发现路径。	单轮计算可饱和更多路径，能更快地逼近网络最大流通能力，加速容灾方案生成。
动态适应性	路径搜索相对盲目，网络局部变化（如链路故障）可能导致后续搜索效率进一步降低。	通过分层图自然感知网络拓扑变化。每次BFS都能快速重建对当前网络结构的认知。	能快速适应网络状态变化（如链路中断、带宽调整），及时重新计算最优流，提升容灾系统的鲁棒性。

这些优势在动态网络容灾中的具体体现:

更智能的路径探索策略

Dinic算法通过分层图 技术，为网络"绘制"了一张导航图。它首先使用广度优先搜索（BFS） 为每个节点标记其到源点的最短距离（层数），形成分层图。随后，在增广阶段，它使用深度优先搜索（DFS） ，但规定每次只探索从当前层指向下一层的边。

避免迂回搜索：这种方法确保了每次寻找的增广路径都是当前最短路径之一，避免了Ford-Fulkerson算法可能陷入的反复寻找低效长路径的问题。在动态网络中，这意味着能更快地发现关键连通路径和瓶颈。
多路增广：在同一个分层图上，Dinic算法可以进行多次DFS，尽可能多地找到并饱和（即用完容量）该层级结构下的所有增广路径。这好比在建设容灾路由时，一次性规划并开通一个方向上的多条并行通道，而不是像Ford-Fulkerson那样一条一条地试探。

可预测的高效计算

Dinic算法具有强多项式时间复杂度 O(V²E)。这意味着它的运行时间上界仅由网络本身的拓扑结构（节点数V和边数E）决定，而与链路的容量大小无关。

在动态网络容灾中，链路的剩余带宽（可看作容量）可能随时变化。Dinic算法的这一特性保证了无论网络带宽如何波动，计算最大流所需的时间都是相对可控和可预测的。这对于需要快速响应故障并进行流量调度的容灾系统至关重要，因为它提供了性能底线保障。相比之下，Ford-Fulkerson算法的效率则依赖于每次找到的增广路径所能增加的流量，在不利情况下（如容量很大但路径效率低）可能非常缓慢。

增强容灾计算的鲁棒性

动态网络的容灾计算需要算法能快速适应拓扑变化，如链路故障或节点失效。

快速感知与重构 ：当网络发生故障时，Dinic算法在下一轮计算中会立即通过BFS重建分层图。这个过程能自然地感知到网络连通性的变化（例如，某条链路中断后，某些节点会变得不可达或其层数会增加）。算法基于新的分层图进行计算，结果能准确反映故障后的网络状态。
稳定性与可靠性 ：由于Dinic算法不依赖于特定路径的查找运气，其性能波动较小。这种稳定性使得容灾控制系统能够可靠地评估网络的幸存容量和规划恢复路径，不会因为算法本身的不确定性而引入额外风险。

总结

总而言之，Dinic算法通过其分层图建模、多路增广机制和强多项式时间复杂度 ，在动态网络容灾计算中提供了远超基础Ford-Fulkerson算法的效率、适应性和可靠性。它使网络管理系统能够更快、更准确地评估灾难影响，计算有效的流量迁移方案，从而显著提升整个基础设施的韧性和自愈能力。

1.8.12 迟滞机制

在实际系统中，有效的迟滞机制是稳定系统的"减震器"，它的核心思想是：让状态切换变得"迟钝"一些，避免系统在临界点附近因微小波动而频繁跳动。

迟滞机制的核心设计原则

迟滞机制的设计万变不离其宗，其核心思想在于为系统的状态切换引入"惯性"，主要依赖以下几个关键原则：

核心原则	设计思路	实现效果
定义清晰的双阈值与死区	设置不同的触发阈值和恢复阈值，并在两者之间形成一个"安全区"或"死区"。	系统状态必须在稳定地越过恢复阈值后，才会切回正常状态，有效过滤短时抖动。
引入状态记忆与历史依赖	将历史状态作为当前决策的关键输入之一，使系统具备"惯性"。	当前状态倾向于保持与之前一致，避免因瞬时干扰而翻转，增强抗干扰能力。
采用渐进式调整与非瞬时切换	状态切换不应该是瞬时的，可引入计时器或渐进式调整。	进一步保证状态变化的稳定性，避免反应过度。
设计状态隔离与安全过渡	在复杂系统中，为不同状态设计独立的检测与切换逻辑。	防止状态间相互干扰，并在状态切换时管理好相关的资源与流程，确保安全过渡。

结合具体案例看设计

理论可能有些抽象，我们通过几个具体案例来看看这些原则是如何应用的。

1. 网络熔断器：应对服务依赖故障

在微服务架构中，熔断器（Circuit Breaker）是使用迟滞机制的经典场景，其目的是防止连锁故障。

工作逻辑 ：熔断器通常有关闭（正常请求）、打开（快速失败）和半开（试探性恢复）三种状态。
迟滞设计：
- 双阈值 ：当错误率持续一段时间 （而不仅仅是某一瞬间）超过某个阈值（如50%）时，熔断器才从"关闭"状态切换到"打开"状态。当熔断器进入"打开"状态后，它会持续一段时间（如5秒），在此期间拒绝所有请求。这段时间就是强制"死区"，无论期间是否有零星成功请求，都不会立即关闭。
- 状态记忆与渐进恢复 ：经过强制等待期后，熔断器不会直接关闭，而是进入"半开"状态。在此状态下，它会放行少量试探请求 。只有这些试探请求的成功率稳定在较高水平（另一个恢复阈值），熔断器才会最终切换到"关闭"状态。bRPC框架就采用了类似的指数退避策略来动态调整隔离时长，并利用半开状态下的成功计数来进行渐进式恢复。

2. 高速通信表决器：抑制瞬时干扰

在高速串行通信的接收端，需要判断采样时钟相位是超前还是滞后于数据跳变沿。由于信道噪声，直接根据瞬时采样结果表决会因干扰而产生误判。

工作逻辑：表决器需要根据多个采样点的结果（如10个），通过"少数服从多数"的原则输出一个最终判断。
迟滞设计：
- 历史依赖 ：一种先进的迟滞表决器设计，会将当前时刻的采样数据与前几个时钟周期的表决结果进行综合统计（例如，统计前3个周期内至少出现2次相同结果），共同参与新一轮的表决。
- 效果：这意味着，如果之前的判决结果一直是"超前"，那么即使当前瞬时采样数据出现轻微波动（比如10个输入中有5个"超前"5个"滞后"），表决器也更倾向于维持"超前"的判断。这有效抵抗了瞬时大干扰，提高了时钟恢复电路的稳定性。

3. 监控告警系统：避免告警风暴

运维监控系统中，如果CPU使用率在85%上下跳动，若不处理，可能会触发大量重复告警。

工作逻辑：监控系统需要判断某个指标（如CPU使用率）是否异常。
迟滞设计：
- 双阈值与持续时间 ：可以设置告警触发阈值为90%，但恢复阈值设为80%。同时，增加持续时间判断 ，例如要求CPU使用率连续超过90%长达1分钟 才触发告警，而恢复则需要连续低于80%持续2分钟才清除告警。
- 动态基线 ：更智能的系统会结合历史数据建立动态基线。例如，Codis的监控优化中，会计算过去7天相同时段的指标均值作为基线，只有当当前指标持续且显著地偏离（如超过3个标准差）这个基线范围时才触发告警，这本身也是一种考虑历史规律的迟滞。

总结与最佳实践

设计一个有效的迟滞机制，本质上是在系统的灵敏度和稳定性之间寻找最佳平衡点。你可以遵循以下路径：

分析波动特性：首先观察和理解系统指标的正常波动范围和周期性规律。
定义清晰的状态与切换条件 ：明确系统有哪些状态，以及状态切换的触发条件 和恢复条件。
设置双阈值与死区：根据第一步的分析，合理设置触发和恢复阈值，形成缓冲区域。
引入时间维度和历史权重：使用持续时间判断，并决定历史数据在当前决策中的权重。
测试与迭代：在模拟环境或小范围生产环境中测试迟滞规则，根据告警数量、响应时间等指标进行微调和优化。

1.8.13 迟滞机制的阈值设计

在分布式系统中，迟滞机制通过设置两个不同的阈值（例如一个用于触发动作，一个用于恢复常态）来防止系统在临界点附近频繁波动，从而提升稳定性。其双阈值设置确实存在一些值得遵循的通用原则。

通用原则	核心目标
1. 创建稳定的"死区"	防止状态在临界点附近频繁切换（抖动），提升系统稳定性。
2. 考虑系统惯性	为有启动/停止开销的操作预留足够的时间窗口，避免无效操作。
3. 权衡性能与一致性/可用性	根据系统在PACELC定理下的侧重点（如强一致性或低延迟）调整阈值敏感度。
4. 减少振荡与资源浪费	降低不必要的资源分配/释放、状态同步带来的开销。

原则详解与场景分析

下面我们深入探讨这些原则的具体含义和应用。

1. 保持"死区"宽度以抑制抖动

迟滞机制的核心是在两个阈值之间建立一个非敏感区或"死区"。例如，若设置CPU使用率超过80%开始扩容，那么恢复（缩容）阈值不应也设为80%，而应设置为更低的数值（如60%）。这确保了即使指标在80%附近小幅波动，系统也不会出现扩容后立刻缩容的振荡行为。这个"死区"的宽度应根据监控指标本身的正常波动范围来确定。

2. 为系统"惯性"预留缓冲

许多分布式操作本身存在"惯性"，即从触发到完全生效需要时间。例如：

资源调度：开启一台虚拟机或一个容器实例需要时间。如果恢复阈值设置得与触发阈值过于接近，新启动的资源可能还未完全承接负载，系统就因为观测到指标短暂下降而触发缩容，导致无效操作。
一致性同步：在分布式数据库中，写操作的传播和确认需要时间。设置适当的迟滞区间可以避免因网络短暂延迟或队列抖动而误判节点不可用，从而减少不必要的领导者切换。

因此，阈值间隔应大于相关操作的典型完成时间。

3. 对齐系统的核心权衡

根据PACELC理论，分布式系统需要在正常运行时权衡延迟和一致性。这一权衡直接影响阈值设置：

偏向强一致性的系统：这类系统可以容忍较高的操作延迟来保证数据正确性。例如，其故障切换的阈值可以设置得相对"迟钝"一些，确保只有在确凿无疑发生故障时才触发主从切换，哪怕这会增加几秒钟的不可用时间。
偏向低延迟和高可用的系统：这类系统可以接受短暂的数据不一致。其阈值可以设置得相对"敏感"，以便快速响应变化，例如快速将流量从疑似故障的节点上切走，优先保证服务可用性。

常见场景中的阈值设置

计算资源弹性伸缩 ：如在云数据中心中，设置扩容阈值（T1）和缩容阈值（T2），并确保 T1 > T2。为避免备用集群频繁启停，缩容阈值T2可设置为N1-1（N1为基础集群大小），而扩容阈值T1应小于备用集群大小N2，以确保激活后能处理缓冲队列。
数据存储与复制：对于主从复制的数据库，判定主节点失联并触发切换的时间间隔应设置迟滞。例如，连续3次心跳超时（而不仅仅是1次）才判定节点故障，以避免因网络瞬时拥塞导致不必要的切换。
集群协调与服务发现：服务健康检查的间隔和超时时间设置也体现了迟滞。例如，允许连续失败检查的次数，就是一种迟滞设计，防止因一次网络抖动就将健康实例从注册中心剔除。

1.8.13 迟滞机制和PID控制应对不确定性和扰动

迟滞机制和PID控制都是控制系统设计中应对不确定性和扰动的有效工具，但它们解决问题的思路和适用场景有显著差异。下面这个表格可以帮你快速把握它们的核心异同。

特性维度	迟滞机制	PID控制
核心目标	维持状态稳定，防止在阈值附近频繁、反复地切换动作。	精确跟踪目标，通过减小系统输出与期望值之间的偏差来实现控制。
工作原理	设置双阈值（高/低），形成"死区"。动作的触发不仅取决于当前值，还依赖于历史状态。	对误差信号进行比例（P）、积分（I）、微分（D）的线性组合运算，产生控制信号。
关键特征	非线性：特性由阈值差决定；路径依赖：系统的行为与如何到达当前状态有关。	线性：在非饱和状态下，输出与输入误差成线性关系；即时响应：输出直接由当前及最近的误差历史决定。
主要优势	有效消除抖动，减少部件磨损和无效操作，极大提升系统在临界点附近的稳健性。	结构简单，适应面广，对于许多线性或近似线性的系统，通过参数整定即可获得良好效果。
典型场景	恒温器控制（如超过71°F关加热，低于69°F才开加热）、设备启停保护、数字信号去抖。	汽车定速巡航、无人机姿态稳定、化工过程反应器温度控制等需要连续、精确调节的场合。

本质区别：不同的解决思路

尽管目标都是提升系统性能，但两者源于不同的哲学。

PID控制：基于"纠正偏差"的连续思维

PID控制器是一种连续、线性的反馈控制器 。它时刻计算着目标值与实际输出值之间的误差（e(t)），并通过对该误差进行比例、积分、微分的加权求和，来生成一个能够不断减小这个误差的控制力。其核心思想是 **"持续微调，精准打击"** 。例如，在精密定位系统中，PID控制器能持续输出微小的控制电压，驱动执行机构以高精度到达目标位置。
迟滞机制：基于"提高决策容错"的阈值思维

迟滞机制本质上是一种非线性的开关控制或决策策略 。它通过引入一个"死区"（Deadband）------即动作阈值和复位阈值之间的区间，来容忍系统在设定点附近的正常波动。其核心思想是 **"谋定而后动，避免手忙脚乱"** 。它不关心如何精确到达某一点，而是确保系统状态在跨越一个明确的边界后，才会产生一个确定的、大幅度的动作改变，并且这个改变不会因为微小的扰动而立刻反转。这在控制继电器的通断、防止水泵频繁启停等场景中至关重要。

如何选择与结合使用

在实际工程中，迟滞机制和PID控制并非互相排斥，而是常常协同工作，甚至融合在一起，形成更高级的控制策略。

独立应用场景
- 当你的控制对象本身就是一个开关量 （如电热丝的通断、电机的启停），且主要矛盾是防止在临界点附近频繁动作时，优先选用纯迟滞机制。
- 当你的控制对象需要连续、平滑、精确的调节（如阀门的开度、伺服电机的转速），并且系统模型相对明确时，PID控制通常是首选。
协同工作模式
- 层级协作：在复杂的系统中，PID控制器可能作为"调节者"，而迟滞机制则作为"决策者"位于上层。例如，一个温控系统可能使用PID算法来精细计算所需的加热功率，但最上层的管理策略可以是一个迟滞开关，决定在何时整体启动或停止这套PID温控系统，以避免短周期循环。
- 深度融合 ：为了克服传统PID积分环节在系统启动或设定值突变时容易引起的"积分饱和"（Windup）现象，可以引入一种具有迟滞特性的抗积分饱和机制。当检测到控制器输出即将达到执行机构的极限时，暂时"冻结"积分作用，待输出回到合理范围后再恢复，这有效结合了迟滞的"开关"思想和PID的"连续"控制。

迟滞机制与PID控制是应对不同控制需求的两种利器。PID是一位精益求精的"微操大师"，致力于通过持续调整实现精准定位；而迟滞机制则是一位富有远见的"战略家"，通过提高决策门槛来确保系统在大局上的稳定和高效。

在实际的复杂系统中，单纯使用PID控制或迟滞机制往往难以满足所有要求。将两者结合，可以发挥PID控制精确调节的优势，同时利用迟滞机制增强系统的稳定性和鲁棒性。

系统类型	主要挑战	PID控制的作用	迟滞机制的作用	协同工作方式
热泵过热度控制	大时滞、强耦合、非线性	进行精细调整，减小稳态误差	通过模糊规则实现平滑切换，防止模式频繁振荡	并联结构，权重混合
电动加载系统（EDLS）	周期性多余力矩、控制时滞	抑制非周期性干扰，保证系统初态一致	迭代学习补偿周期性扰动，记忆历史误差	层级分工，迭代优化
压电陶瓷纳米定位	迟滞非线性、蠕变	作为主控制器进行反馈调节	逆模型前置补偿，非线性积分抑制积分饱和	前置补偿，智能积分
时滞系统（如温度控制）	信号传输或处理延迟	基础反馈控制	Smith预估器提前计算补偿量	预测补偿，前馈协同

协同工作原理深度解析

上述系统中的协同策略，体现了迟滞机制与PID控制结合的几种核心思路：

权重混合与平滑过渡 ：在热泵过热度控制这类系统中，迟滞机制并非一个独立的控制器，而是作为一种决策逻辑 。它根据系统当前的误差大小，动态地调整模糊控制和PID控制输出在总控制量中的混合权重。这种权重变化是平滑的，而非突跳的，从而避免了控制模式的频繁切换或输出剧烈波动，保证了系统的平稳运行。
层级分工与记忆学习 ：在面对周期性扰动时，如电动加载系统中的多余力矩，可以采用层级式设计 。PID控制器作为底层基础，负责维持系统的稳定性和抗随机干扰。而迭代学习控制（ILC）作为一种具有"记忆"功能的迟滞机制，运行在更高层级，它利用前一周期的误差信息，不断修正当前周期的控制指令，从而主动地、前瞻性地消除周期性扰动，实现了PID难以做到的精确跟踪。
前置补偿与智能调节 ：对于压电陶瓷执行器固有的迟滞非线性，最有效的策略是串级补偿 。首先，用一个精确的迟滞逆模型作为前置滤波器，将非线性系统"补偿"成一个近似线性的系统。然后，PID控制器再对这个线性化后的系统进行控制。此外，通过引入非线性函数改造PID控制器的积分项，使其对小误差敏感（放大），对大误差不敏感（饱和），这种智能积分本身就是一种迟滞行为，能有效抑制积分饱和，提高控制品质。

总结

总而言之，在复杂系统中，迟滞机制与PID控制并非替代关系，而是互补与增强 的关系。PID控制器提供精确、连续的调节能力 ，而迟滞机制则贡献了状态记忆、智能切换、前瞻补偿和振荡抑制等高级功能。

1.8.14 持续同调如何量化网络拓扑韧性

持续同调的核心优势在于它能跨越多个尺度 来捕捉拓扑特征的"出生"和"死亡"，并通过分析其"生命周期"的长短来区分稳健的结构特征 和短暂的噪声波动。

关键指标：贝蒂数与条形码
- 贝蒂数 ：在特定尺度下，β₀ 表示连通分量数量，β₁ 表示环形孔的个数，β₂ 表示空腔的数量。它们直观反映了网络在该尺度下的拓扑结构。
- 条形码图 ：持续同调的核心可视化工具。每条线段代表一个拓扑特征（如一个连通分量或一个环），其起始点和长度分别表示该特征在过滤过程中"出生"和"死亡"的尺度，以及其存活的"生命周期"。生命周期长的特征 （长条形码）通常对应网络中稳健的、固有的拓扑结构 （如核心骨干连接）；而生命周期短的特征 （短条形码）则可能源于噪声或瞬时波动。
量化韧性：从条形码到韧性指标

网络的拓扑韧性可以理解为这些拓扑特征抵抗扰动（如节点/链路故障）而保持不变的能力。持续同调通过以下方式量化它：
- 特征持久性分析：比较故障前后或不同扰动下条形码图的变化。如果关键拓扑特征（长条形码）在扰动下依然稳定存在，表明网络在该维度上具有高韧性。
- H(k)-核分解与关键特征识别 ：如中所述，H(k)-核分解方法通过逐步删除特定节点和边来简化网络，同时保留关键拓扑特征（如高阶洞）。这有助于识别出对网络连通性至关重要的"拓扑骨架"。该骨架的稳健性直接关系到整体网络的韧性。
- 动态网络拓扑演化追踪 ：对于动态网络（如中研究的多图格），持续同调可以追踪拓扑特征随时间的演化。例如，β₀（连通分量数）的减少可能反映系统的整合过程，而β₁（一维环）的变化可能对应功能环路的形成与重塑。通过观察不同尺度下特征演化的稳定性，可以评估网络动态韧性。

持续同调如何改善迟滞机制

迟滞机制的核心是在状态切换点附近引入"死区"以防止抖动。持续同调可以为优化迟滞机制提供基于拓扑结构的、更精细的决策依据。

提供拓扑视角的阈值设定依据

传统的迟滞阈值往往基于经验或单一性能指标（如CPU利用率）。持续同调分析可以揭示出网络层面的结构性临界点 。例如，条形码图中条形码大量"死亡"所对应的尺度区间，可能标识了网络结构发生显著改变的临界区域。迟滞机制的阈值（如触发故障切换或资源重配的阈值）可以参考这些拓扑临界点来设置，使得系统响应与底层网络结构的实际变化更同步。
识别对迟滞敏感的关键拓扑结构

通过分析条形码图，可以识别出那些"生命周期"处于临界区域、对系统状态变化敏感的拓扑特征（如某些特定的环或空腔）。这些特征可能正是导致系统在特定负载或故障场景下产生振荡或不稳定的潜在原因。迟滞机制的设计可以特别关注这些敏感结构的变化，例如为其设置更保守或更激进的迟滞区间，以实现更精细化的控制。
动态调整迟滞参数

在动态网络或变化的工作负载下，理想的迟滞参数可能不是固定的。结合实时或近实时的持续同调分析（尽管计算挑战较大），可以感知网络拓扑结构的变化趋势。例如，当监测到关键拓扑特征的持久性开始下降时，可以动态调整迟滞机制的参数（如缩小"死区"以提高灵敏度，或扩大"死区"以增强稳定性），使迟滞机制能够适应网络状态的变化。

持续同调如何指导容灾策略

容灾策略的制定需要准确识别脆弱点并规划 resilient 的恢复路径。持续同调提供了超越传统图论的工具。

精准识别脆弱环节
- 高阶拓扑视角 ：传统图论关注点、边故障，而持续同调（特别是高阶同调，如 β₁, β₂）能揭示多个组件协同故障对网络连通性的影响。例如，中提到的高阶洞（high-order holes）反映了网络深层中的对称结构，其稳定性与网络动力学稳健性相关。
- 量化损伤程度 ：通过比较正常状态与模拟故障状态（如移除部分节点或边）下的持续同调条形码，可以量化故障对网络拓扑结构的损伤程度。哪些特征的"死亡"尺度提前了？哪些长生命周期特征消失了？这为脆弱点评估提供了量化指标。
指导冗余设计与备份路径规划
- 韧性区域识别 ：条形码图中那些生命周期极长的拓扑特征所对应的子网络，往往是网络的核心韧性区域。容灾设计时应优先保障这些区域的可靠性。
- 备份路径优化 ：在规划备份路径时，可以考虑使其绕过在故障模拟下表现出短暂生命周期的拓扑特征（脆弱区域），或者优先利用那些在多种故障场景下都保持稳定的拓扑特征所构成的路径。这有助于规划出更具韧性的通信或恢复路径。
容灾策略有效性验证

可以针对设计好的容灾策略（如特定的备份路径或切换方案）进行持续同调分析，模拟在故障发生时，采用该策略后网络拓扑特征的变化情况。如果关键特征的持久性得到较好保持，说明该策略有效维护了网络的拓扑完整性。

总结与挑战

持续同调分析为网络拓扑的韧性评估、迟滞机制优化和容灾策略制定提供了一个强大且深刻的数学视角 。它将容灾设计的焦点从简单的连通性判断，提升到了对网络深层拓扑结构稳健性的关怀。

然而，也需要意识到其挑战：

计算复杂度：对于大规模网络，持续同调的计算成本较高。
实时性：完全的实时分析目前较难，多用于离线规划、阶段性评估或结合轻量化近似方法。
结果解读：需要专业知识将拓扑特征（贝蒂数、条形码）映射回具体的网络元件和业务逻辑。

要让持续同调分析这项强大的拓扑工具，从"离线分析"走向"实时监控"，关键在于大幅降低其计算复杂度。这需要通过一系列技术，在分析的各个阶段进行优化，在保证洞察力的同时，提升计算速度。

优化阶段	核心策略	实现方式	预期效果
① 数据预处理	智能过滤与简化	基于H(k)-核分解等方法保留关键节点/边；对数据进行降维（如PCA）和去噪。	从源头削减需分析的网络规模，降低构建复形的复杂度。
② 算法优化	增量计算与近似算法	增量式持续同调：仅重新计算变化部分；采用近似算法（如PHSsBoW）。	避免全量计算，将计算复杂度从 O(n³) 级别显著降低。
③ 并行计算	分布式与GPU加速	将复形构建、边界矩阵计算等任务并行化（如使用Spark、GPU）。	利用多核或多机资源，将大规模计算任务分解后并行处理。
④ 架构设计	分层与自适应监控	分层监控：仅在检测到显著变化时触发全尺度分析。	将计算资源集中于最关键的时段和区域，避免不间断的全网计算。

数据预处理与过滤

在进行分析前，对网络数据进行"瘦身"至关重要。

聚焦关键结构 ：可以使用像 H(k)-核分解 这样的方法，识别并保留网络中连接最紧密、最核心的部分，过滤掉相对不重要的边缘节点。这能在很大程度上简化网络，而不丢失其主干拓扑特征。
数据降维与去噪 ：对于高维特征数据，可以先使用主成分分析（PCA） 等线性或t-SNE、UMAP等非线性降维技术，在保留大部分拓扑结构信息的同时减少数据量。同时，清除数据中的噪声点，因为这些点可能会产生大量短暂且无意义的拓扑特征，干扰分析。

算法层面的核心优化

这是降低计算复杂度的主战场。

增量计算 ：实时监控中，网络状态通常是连续变化的，但大部分变化是局部的。增量式持续同调算法 的核心思想是，当网络增加或删除少量节点/边时，不再重新计算整个网络的持续同调，而是基于上一次的计算结果，仅对受影响的部分进行更新。这就像只修补发生变化的那块地图，而不是每次都重新绘制整张地图，效率提升巨大。
采用近似算法 ：有时我们不必追求百分百精确的同调群计算。可以牺牲少量精度以换取计算速度的数量级提升 。例如，有研究提出了 PHSsBoW、PHSwBoW 等算法，通过将持续性图（Persistence Diagrams）向量化为固定长度的特征，或者使用随机采样的方法来估算拓扑特征，这些都能极大加速计算过程。

并行计算与硬件加速

持续同调分析中的许多步骤，如构建Vietoris-Rips复形、计算边界矩阵、矩阵约简等，天然适合并行处理。

利用并行框架 ：可以将这些任务部署在Spark、GraphX 等分布式计算框架上，或者利用GPU 的大规模并行计算能力进行加速。通过将大规模问题分解成多个子任务同时在多个核心或机器上运算，可以显著缩短计算时间，满足近实时监控的需求。

系统架构与监控策略

在工程实现上，聪明的策略也能有效减轻计算负担。

分层监控策略 ：模仿电力系统中对微电网的同调分群等值 思想，可以不对整个巨型网络进行持续同调分析。而是先根据电气耦合紧密程度等因素，将大网络划分为若干个动态同调区域。监控系统可以主要关注各个区域内部的局部拓扑变化，以及区域之间的连接关系。只有当某个区域内部发生剧烈变化（如检测到潜在的"分裂"风险）时，再针对该区域进行更精细化的持续同调分析。这种"抓大放小"的策略能极大节约计算资源。
自适应采样与触发 ：不必以极高的频率不间断运行持续同调分析。可以结合简单的阈值告警（如特定链路带宽利用率骤变）、或基于滑动窗口统计 的方法，当检测到网络状态发生显著变化时，才触发一次持续同调分析。在相对平稳的时期，则可以降低分析频率。

总结与实施路径

将持续同调分析用于实时韧性监控是一个系统工程。没有单一的"银弹"，需要综合运用上述多种策略。一个可行的实施路径如下：

建立基线：首先对网络在正常状态下的拓扑进行完整的持续同调分析，得到基准的持续性图（作为"健康图谱"）。
实施监控 ：在线上部署经过算法优化 （增量计算、近似算法）和工程优化（并行计算）的轻量级持续同调分析模块。
智能触发 ：采用分层监控 和自适应触发 策略，决定何时、对哪部分网络进行深度拓扑扫描。
评估与告警：将实时计算出的拓扑特征（如Betti数的变化、重要拓扑特征的"死亡"）与基线进行比对，一旦发现表征网络韧性严重下降的迹象（如标志网络连通性的环状结构持续消失），则产生高级别告警。

持续同调作为拓扑数据分析中的先进数学工具，能帮助我们更深刻地理解网络的"形状"与"韧性"，从而指导设计出更智能的容灾策略。它通过分析网络在各种"尺度"下的连通性特征（即拓扑不变性），实现对网络脆弱点的精准定位和恢复路径的优化。

特性维度	传统容灾方法	持续同调指导下的容灾策略	核心改进点
脆弱性识别	关注单点（节点/链路）故障，静态、局部。	全局、多尺度分析网络结构，识别关键连接区域和潜在瓶颈。	从"治已病"到"防未病"，提前发现结构性风险。
恢复路径设计	常依赖预设的固定备用路径，灵活性差。	动态计算拓扑结构最优且负载均衡的逃生路径，避免次生拥塞。	恢复路径更健壮、更高效，提升整体恢复成功率。
资源分配效率	资源平均分配或简单按优先级分配，可能浪费或不足。	精准定位对网络连通性贡献最大的组件，实现资源优化投放。	在同等投入下，显著提升整体网络的韧性。
策略验证与模拟	主要靠压力测试和故障演练，成本高、周期长。	可在仿真环境中快速推演多种故障场景对网络拓扑的影响，优化策略。	加速容灾方案迭代，降低试错成本，提升预案可靠性。

持续同调如何工作

您可以把持续同调想象成一个能够进行"CT扫描 "的工具。它不像传统方法那样只数清网络中有多少条路（节点和链路），而是能揭示出这些路是如何连接成环状或空腔等更高阶的拓扑结构。

构建"尺子"：它通过一个连续的参数（如链路延迟阈值或丢包率阈值）来"扫描"网络。这个参数就是"尺子"。
观察"出生"与"死亡" ：随着"尺子"的变化，网络拓扑会发生变化。持续同调追踪这些拓扑特征（如环路、空腔）的**"出生"（出现）和"死亡"（消失）**。
生成"条形码" ：每个拓扑特征都会在一条时间线上被表示为一小段"条形码"。条码的长度 代表了该拓扑特征的持久性 。存活时间越长的特征，通常对应网络中越稳定、越核心的结构。

基于这种分析，我们可以识别出网络中那些对全局连通性至关重要的"骨干结构 "，以及那些相对脆弱、容易在压力下失效的"局部结构"。

真实场景的改进案例

案例一：数据中心网络韧性提升

在提到的B站机房光缆中断故障中，其DCDN架构虽然通过源站级别的容灾保证了核心业务稳定，但也反映出在面对某些极端故障时，快速定界和部分非多活业务的手动切流仍存挑战。若引入持续同调分析，可以对整个数据中心的网络拓扑进行"CT扫描"，生成其独有的"韧性条形码"。通过分析这些条形码，运维团队可以：

精准预判瓶颈 ：提前识别出那些看似不重要、但一旦失效会显著增加网络直径或导致网络分割的关键链路（其失效会导致长寿命的拓扑特征"死亡"）。
优化逃生路线 ：在故障发生时，控制系统可以依据实时计算出的拓扑"条形码"，动态生成绕过当前故障区域且对全局拓扑损伤最小的最优恢复路径，而不是依赖静态的备用路由。这类似于在中期望实现的更快速甚至自动化的止损方法，特别是对于非多活业务，持续同调可以为其规划出高效的"逃生通道"，通过内网专线转发流量。
指导网络建设 ：在介绍的福州"数智创新韧性城市安全新范式"中，通过布设各类传感器构建了城市生命线的监测网络。持续同调分析可以评估此类复杂物联网络的结构韧性，指导在最关键的位置部署监测设备，避免监测盲区，从而提升类似福州积水监测平台那样的全域感知能力。

案例二：物联网韧性优化

物联网终端通常通过多个网关接入网络。传统方法可能只关注单个网关的负载或信号强度。

持续同调的洞察 ：通过持续同调分析物联网的连接拓扑，可以发现那些对维持整个网络连通性至关重要的"枢纽"网关。这些网关的失效可能导致大面积设备失联。
具体改进：
- 主动防护 ：对这些识别出的关键网关实施重点监控和资源保障，比如提供更稳定的电源和网络回程。
- 动态重构 ：当某个区域网关故障时，系统可依据实时拓扑分析，智能引导终端切换到能最佳维持该区域连通性的备用网关，而不是简单地连接到信号最强的网关，从而避免网络被分割成无法互通的孤岛。这种基于网络整体拓扑的智能决策，远超传统方法。

持续同调指导下的容灾策略，其核心优势在于它将容灾设计从基于局部经验和静态配置 的传统模式，提升到了基于网络全局结构和动态洞察的新高度。它使我们能够：

量化评估韧性：用数学语言精确描述网络的健壮性。
预见性防护：提前发现并加固网络中的"阿喀琉斯之踵"。
动态智能恢复：在故障发生时，快速计算出最优恢复策略。

1.8.15 金融交易中基于持续同调的功能韧性评估框架

对于金融交易这类实时性要求极高的业务，基于持续同调的功能韧性评估框架确实需要特别的设计。其核心在于，评估本身不能成为系统的负担，并且评估结果必须能直接、快速地映射到业务关键指标上。

设计维度	核心目标	金融交易场景下的特殊考量
实时性与计算效率	评估过程必须极快，不能影响正常交易。	采用增量计算和近似算法，仅分析网络局部变化或采样关键路径，将分析延迟控制在微秒到毫秒级。
业务指标映射	评估结果需直接反映对交易业务的影响。	将拓扑特征（如β₁环路）与交易延迟、订单吞吐量、撤单率等直接挂钩，量化链路中断对业务SLA的潜在破坏。
故障模拟与针对性	重点测试对金融系统危害最大的故障场景。	优先模拟主机柜网络分区、核心交换机故障、订单队列堆积等高频高危场景，而非泛泛测试。
与风控系统集成	评估结果需能触发实时的风险控制。	框架应与现有熔断机制、流量调度系统联动。一旦预测到韧性临界点，可自动启动应急预案，如将交易切换到灾备中心。

关键设计思路详解

除了表格中的核心点，还有几个关键思路可以帮助框架更好地服务于金融交易场景。

定义业务层面的"韧性临界点"

在金融交易中，仅仅"网络连通"是远远不够的。框架需要定义更精细的业务韧性临界点 。例如，这可能是交易延迟超过10毫秒 ，或订单成功率低于99.999% 。持续同调分析的目标，就是要在网络拓扑结构的变化（如冗余环路的减少）导致业务指标逼近这些临界点之前，就发出预警。这使得韧性评估从网络连通性判断，升级为业务连续性的前瞻性保障。
构建动态的"韧性拓扑图谱"

金融交易网络并非静态。随着虚拟化资源和云原生技术的运用，服务的实例和网络路径会动态变化。评估框架需要能感知这种变化，实时构建或更新当前的逻辑拓扑图。这意味着框架需要与服务网格 或云管理平台集成，确保分析的拓扑图与实时运行的系统保持一致，避免基于过时的拓扑做出错误判断。
与现有高可用架构协同

金融系统通常已具备成熟的高可用架构，如细胞（Cell-Based）架构 或同城双活/异地多活 架构。持续同调框架不应取代它们，而是作为增强层 。例如，它可以用来评估单个细胞内部的冗余度是否充足，或者在多活数据中心之间，是否存在多条独立物理路由的冗余路径，从而验证现有高可用设计的有效性。

参考案例：从失败中学习的重要性

芝商所（CME）在2025年发生的宕机事件是一个深刻教训。其灾备中心未能成功启用，暴露出灾备体系与实际业务脱节 的"纸面冗余"风险。这提醒我们，基于持续同调的韧性评估绝不能是纸上谈兵。它必须通过定期的混沌工程测试，在真实但可控的环境中模拟故障，验证评估框架的预测是否准确，以及预设的应急流程是否真的有效。一个未经实战检验的韧性框架，是不可靠的。

总而言之，为金融交易系统设计持续同调功能韧性框架，关键在于实现 "快速、精准、联动"：

快速：通过增量计算和近似算法，满足毫秒级的实时性要求。
精准：将拓扑分析与核心业务指标（延迟、吞吐量）紧密映射，确保评估结果直接反映业务风险。
联动：与现有的高可用架构、风控和运维体系深度融合，使评估结果能够触发有效的应对行动。

在金融交易这个不容有失的领域，构建一个能够抵御各种未知扰动、保持核心功能稳定的系统，是至关重要的。持续同调和非线性动力学为这一目标提供了强大的理论武器，帮助我们打造出不仅能抵抗故障，更能从故障中学习和进化的韧性系统。

框架层级	核心组成	关键活动与产出
理论基石	持续同调分析：洞察系统组件的深层依赖与连通性。非线性动力学：识别系统临界点与韧性边界。	识别关键韧性路径、定义稳态指标（如P99延迟）、构建系统韧性图谱。
工程实践	故障注入引擎：模拟真实故障。全景监控体系：实时捕捉系统状态。自动化恢复：实现系统自愈。	执行混沌实验（如网络分区、服务中断）、收集可观测性数据、触发预案或动态调整。
评估与进化	韧性度量指标体系：量化评估韧性水平。闭环学习机制：基于实验结果持续优化。	生成韧性评分（如可用性提升至99.999%）、驱动系统架构和预案的迭代更新。

理论基石：从数学到洞察

这个框架的强大，首先源于其坚实的数学基础。

持续同调：看清网络的"骨架"与"冗余"

持续同调是代数拓扑学中用于分析数据"形状"和"连通性"的工具。在金融交易系统的复杂分布式网络中，它可以帮我们超越简单的"是否连通" ，量化分析网络结构的冗余路径 和脆弱环节 。通过计算贝蒂数 等拓扑不变量，我们可以回答：核心交易服务与风控服务之间是否存在多条独立的通信路径 ？如果一条网络链路中断，是否有替代路径避免交易中断？这使我们能预先识别出对业务连续性最关键的核心路径，并针对性加固。
非线性动力学：预见"蝴蝶效应"与系统行为

金融交易系统本质上是非线性的，一个小扰动（如一次微小的延迟抖动）可能通过正反馈循环被放大，导致整个系统剧烈波动甚至崩溃（如"闪崩"）。非线性动力学提供了分析这类复杂行为的工具，如通过吸引子 、分岔理论 来识别系统稳定运行的参数边界。这帮助我们设定更科学的监控阈值和弹性伸缩策略，避免系统在毫不知情的情况下滑向不稳定边缘。

工程实践：从理论到实战

有了理论指导，我们需要一套可重复的工程化实践方法来落地。

精细化故障注入

基于理论分析识别出的关键路径和潜在脆弱点，我们可以设计高价值的混沌实验 。例如，可以模拟证券行业交易系统中典型的故障场景，如中间件服务不可用、数据库响应延迟飙升、甚至网络分区 等，从而验证系统在极端情况下的容错能力和故障恢复时间。实验前，必须明确定义系统的稳态假说，例如"99.9%的交易应在50毫秒内完成"。
深度可观测性

混沌实验的价值取决于我们能从中"看"到多深。需要构建全景监控体系 ，整合指标、日志、链路追踪等多维度数据。这不仅用于验证实验是否破坏了稳态假说，更重要的是，当系统因非线性动力学特性出现异常但未宕机的"灰色故障"时（如订单处理队列持续缓慢增长），强大的可观测性能够帮助我们快速定位根因。
自动化恢复与自适应

最高级的韧性是"自愈"。框架应推动建立自动化恢复机制 。一旦系统检测到自身偏离稳态（如多个节点同时故障），可自动触发预定的恢复流程，如流量切换、服务重启或资源调度 。更进一步，可以探索基于强化学习等AI技术，使系统能根据历史故障和恢复经验，动态调整策略，实现更高阶的智能韧性。

评估、度量与闭环

为了确保框架持续有效，必须建立科学的评估和优化机制。

量化韧性指标

韧性需要被度量。可以建立一套综合指标体系，例如：故障恢复时间 、核心业务在故障期间的性能劣化程度 、系统在达到新稳态前的数据一致性状态等。某银行核心系统通过混沌工程实践，将故障恢复时间从30分钟优化至30秒，这就是一个极佳的韧性度量范例。
持续优化与学习

混沌工程不是一次性的项目，而是一个持续学习、反馈和优化的循环 。每一个实验，无论成功与否，都应产生详细的报告，用于分析系统的薄弱点，并驱动开发团队进行修复和架构优化。同时，这些经验应沉淀到标准化的故障场景库 和应急预案 中，并纳入CI/CD流程，作为新服务上线前的质量门禁，防止韧性债务累积。

将持续同调的分析洞察与非线性的动态预测能力，通过混沌工程的实验方法应用于金融交易系统，我们能构建的不再是一个仅仅"高可用"的系统，而是一个具备**深刻"洞察力"、强大"抵抗力"和高效"自愈力"** 的功能韧性体系。

这个框架的核心价值在于，它将系统稳定性的保障工作从被动的"故障响应"转向了主动的"韧性构建"，从事后补救转向了事前预防，从依赖个人经验转向了依赖科学的、数据驱动的方法。

如何将抽象的拓扑指标（如贝蒂数）与实际的业务表现（如订单成功率）进行量化关联。这确实是持续同调分析能否在交易系统韧性评估中落地的关键。其核心思路是：将物理或逻辑的网络拓扑特征，视为业务流可靠性的"基础设施骨架"，并通过统计模型或机器学习建立从"骨架健康度"到"业务表现"的预测性或解释性关系。

为了直观展示这一映射关系的建立过程，下图描绘了从拓扑指标到业务指标的核心分析框架：

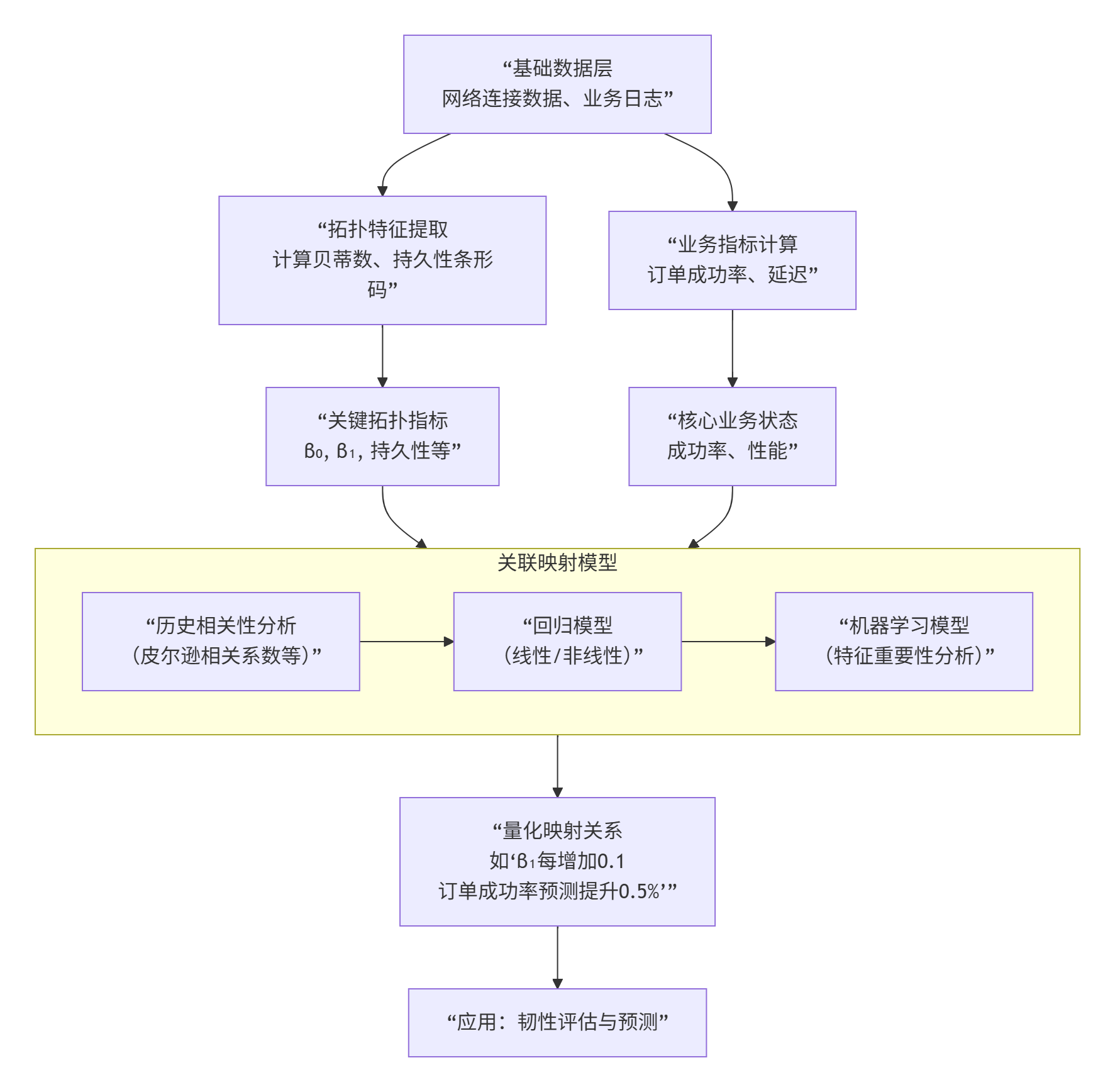
理解拓扑指标的业务含义

首先，我们需要理解贝蒂数这类拓扑不变量在交易系统中可能代表的业务意义。

β₀（零维贝蒂数） 表示网络的连通组件数量 。在交易系统的网络拓扑中，β₀ 的理想值通常为1，意味着所有组件是连通的。如果 β₀ 大于1，则表明网络出现了分裂，部分服务或节点无法通信，这通常会直接导致交易失败或超时。因此，β₀ 的变化可以直接预警大面积服务不可用的风险。
β₁（一维贝蒂数） 表示网络中**"环"或"孔洞"的数量** 。它可以直观地理解为冗余路径的丰富程度 。一个较高的 β₁ 值意味着数据从A点到B点有多条可选的、独立的路径。在交易系统中，高 β₁ 通常意味着更强的容错能力。即使某条网络路径或服务出现延迟或中断，请求仍然可以通过冗余路径成功送达，从而可能维持较高的订单成功率。

建立量化映射关系的方法

理解了业务含义后，就可以通过以下方法建立量化映射关系。

数据准备与同步
- 数据源：收集网络基础设施的监控数据（如网络设备之间的连接和延迟），用于构建拓扑。同时，从应用层面收集业务指标（如订单成功率、平均延迟），并确保两者时间戳对齐。
- 构建持续同调：将特定时间窗口内的网络状态（如节点为服务器或网关，边为连接状态或延迟）转化为点云或单纯复形，计算其在不同尺度（如延迟阈值）下的贝蒂数，并生成持久性条形码。
特征工程与关联分析
- 从持久性条形码中提取特征，例如：
  - 特定维度贝蒂数的均值/最大值：反映整体冗余水平。
  - 拓扑特征的"寿命"：长寿特征通常代表网络中稳定存在的关键冗余结构。
  - 拓扑熵：衡量拓扑结构的无序性或复杂性变化。
- 将这些拓扑特征与相同时序窗口内的**业务指标均值（如订单成功率）** 进行相关性分析（如计算皮尔逊相关系数），初步筛选出与业务表现关联性强的拓扑特征。
构建映射模型
- 回归模型 ：建立拓扑特征（如 β₁ 的移动平均值）与业务指标（如未来一段时间内的订单成功率）的回归模型（线性或非线性）。例如，模型可能显示：预测订单成功率 = 基础值 + k * β₁。通过历史数据拟合出系数k，即可量化影响程度。
- 机器学习模型 ：使用更复杂的模型（如梯度提升树GBDT），将多个拓扑特征（β₀, β₁, 拓扑熵等）作为输入，预测业务指标。模型训练好后，可以进行特征重要性分析，判断哪个拓扑指标对业务稳定性的贡献最大。
- 阈值与预警：根据模型得出的关系，可以设定拓扑指标的预警阈值。例如，当实时计算出的 β₁ 值低于根据历史数据确定的某个分位数时，系统可预测订单成功率有下降风险，从而触发预警。

实践中的考量与挑战

在实际应用中，还需注意以下几点：

选择合适的拓扑构建尺度：根据何种指标（延迟、丢包率）来构建拓扑，会直接影响贝蒂数的计算结果。需要结合具体业务场景进行调试。
区分常态与瞬态 ：短暂的网络抖动可能引起拓扑特征的瞬时变化，但不一定影响整体业务。分析时应更关注拓扑特征的持续性变化趋势，而非瞬时值。
结合领域知识：量化模型需要与系统架构师和运维人员的经验相结合。例如，明确知道某些关键链路的冗余程度对特定业务至关重要，就可以在模型中赋予其更高权重。
动态演进：系统的网络拓扑和业务流量是变化的，因此建立的映射关系需要定期重新评估和校准。

1.9 拓扑韧性指标与网络数据

1.9.1 拓扑韧性指标与实时网络性能数据

将拓扑韧性指标与实时网络性能数据相结合，构建一个综合的功能韧性评估模型：

模型组件	核心输入数据	处理与计算方法	输出/中间指标
结构性韧性指标	网络拓扑图（节点、链路连接关系）	图论算法（如生成树计数、介数/紧密中心性）	生成树数量、节点/链路关键度、网络效率
功能性韧性指标	实时性能数据（带宽、延迟、丢包率）	业务QoS映射、有效路径判定、性能基准比较	路径可用带宽、端到端延迟、QoS满足度
融合与评估模型	结构性指标、功能性指标、业务权重	加权综合评估（如绝对韧性指标）、多阶段评估（准备-吸收-恢复-提升）	综合韧性指数、韧性曲线下面积（衡量抗压与恢复能力）
动态模拟与预测	历史故障数据、当前网络状态	渗流理论、故障传播模拟、基于扩散概率模型的数据重建与预测	渗流阈值（系统崩溃临界点）、韧性演化预测

如何分步构建模型

数据整合与业务映射
- 构建属性增强拓扑图 ：首先，你需要一张包含物理连接关系的网络拓扑图。然后，为其注入"生命" ：为每条链路（边）标注实时或预测的性能数据，如可用带宽、延迟、丢包率 。为每个节点（如路由器、交换机）标注其处理能力、当前负载等。
- 定义业务关键路径与SLA ：识别网络中的关键业务流（如数据中心东西向流量、核心数据库同步流量）。明确每条业务流的QoS（服务质量）要求，例如：必须的保证带宽、最大可容忍延迟和丢包率。这将业务需求量化成了网络必须满足的硬性指标。
计算结构与功能韧性指标
- 结构性韧性 ：利用图论算法计算网络的"骨架"健壮性。例如，计算网络的生成树数量 ，其数值越大，通常意味着网络在部分链路失效后可供选择的冗余路径越多，结构性韧性越高。同时，计算节点/链路的介数中心性等指标，识别出对全局连通性至关重要的核心设备或链路，这些是重点保护对象。
- 功能性韧性 ：针对每条关键业务流，根据其QoS要求（如延迟<10ms）和当前网络性能数据，动态判断是否存在满足条件的"有效路径" 。功能性韧性可以量化为：在给定故障场景下，仍能满足QoS要求的业务流占总关键业务流的比例，或其总吞吐量的保持程度。
建立综合评估模型
- 加权融合 ：最简单的融合方式是为结构性和功能性指标分别分配权重，计算一个综合韧性指数。权重的设定至关重要，应根据业务偏好调整。例如，一个对延迟极度敏感的交易系统，功能性指标中的"延迟满足度"权重就应设得更高。
- 多阶段动态评估 ：一个更先进的模型会考虑韧性随时间变化的完整生命周期。它评估网络在故障发生前（准备阶段 ）的基线性能、故障瞬间（吸收阶段 ）的性能保持能力、故障后（恢复阶段 ）的性能回升速度，以及恢复后（提升阶段）是否达到甚至超过初始水平。通过计算性能曲线下的面积，可以量化网络在完整故障周期内的整体韧性表现。
模拟、预测与资源优化
- 寻找韧性临界点 ：利用渗流理论 等工具，模拟随机或定向攻击下网络的连通性变化。可以逐步提高模拟的"攻击"强度（如随机禁用链路），观察综合韧性指数的衰减情况。韧性指数开始急剧下降的拐点，就是网络的渗流阈值，标识了系统的韧性临界点。这帮助你回答"网络还能承受多大的压力？"。
- 预测与优化 ：可以借鉴扩散概率模型等前沿方法，基于历史数据预测性能指标的演变，从而实现对韧性变化的早期预警。更进一步，可以建立优化模型，在给定的成本约束下（如最多新增K条链路），寻找能使网络韧性（如生成树数量）最大化的链路添加方案。

核心原则与价值

原则1：业务驱动：模型的起点和终点都应是业务需求。所有拓扑和性能指标最终需要映射到对关键业务的影响上。
原则2：动态感知：网络状态是流动的，韧性模型必须能近实时地摄入性能数据，反映当前网络的真实能力，而非静态的纸面规划。
原则3：量化决策 ：该模型最终为决策服务。无论是容灾演练、网络扩容规划，还是故障发生时的应急资源调度，综合韧性指数都能提供一个直观、量化的依据。

1.9.2 基于"韧性中心性"思想的网络组件关键度评估框架

通过量化分析组件故障对业务流量的全局影响来识别关键点

评估维度	核心评估问题	技术实现简述（案例中方案）
结构性影响	该组件失效会导致多少冗余路径消失？网络是否会因此被分割？	模拟断开该设备（如核心交换机），分析网络拓扑的连通分量变化（如β₀指标）和关键冗余环路（如β₁指标）的受损情况。
业务影响	该组件失效会影响哪些关键业务？其SLA（延迟、带宽）如何受损？	通过智能分析平台（如iMaster NCE-FabricInsight）实时追踪业务流，模拟故障并计算受影响业务的流量、延迟变化。
恢复难度	该组件失效后，自动容灾机制（如M-LAG, BGP FRR）的切换效果和时间？	结合网安协同仿真技术，预演故障场景，评估预设的毫秒级切换策略能否生效及恢复时间。

关键组件识别与韧性加固实战

假设某银行拥有一个同城双活数据中心，其核心是两台通过M-LAG（多机箱链路聚合）组网的核心交换机组（Spine-1, Spine-2），下联多个业务区域。

步骤一：结构性影响分析

运维团队会首先模拟核心交换机Spine-1故障。通过拓扑分析发现，尽管其配对设备Spine-2能接管大部分流量，但网络中原有的多条等价路径（ECMP）将立即减少。更为关键的是，某些特定业务（如跨数据中心的数据库同步）的专用路径可能恰好缺乏冗余，只能经过Spine-1。此时，该交换机的"结构性影响"得分会非常高。反之，如果模拟断开一台仅连接少量非关键服务器的接入交换机，可能发现网络连通性完全不受影响，其得分自然很低。

步骤二：业务影响量化

接下来是精准的业务关联。通过智能业务分析平台，可以清晰地看到：

关键业务流量：移动支付交易的流量路径恰好经过Spine-1。
SLA影响 ：模拟显示，Spine-1故障后，即使流量切至Spine-2，由于路径变化和瞬时拥塞，支付交易的延迟可能会从毫秒级跃升至数百毫秒，这将直接违反其SLA。平台甚至可以量化出受影响的交易笔数和潜在的资金损失。这种将组件故障与具体的业务损益关联起来的能力，是"韧性中心性"概念超越传统网络指标的核心价值。

步骤三：容灾能力评估

最后是检验预案。系统会通过数字孪生仿真，运行为Spine-1预设的故障切换预案（如利用M-LAG和BGP快速重路由）。评估重点在于：切换是否为真正的"毫秒级"、是否存在尚未发现的协议震荡风险、以及切换后是否会产生新的瓶颈。通过这种"攻防演练"，可以验证并优化现有容灾策略的有效性。

从识别到行动：制定韧性加固策略

通过以上分析，我们可以得出针对不同关键等级组件的加固策略，核心目标是 "将资源投入到对业务韧性影响最大的地方"。

组件关键度等级	特征	推荐的韧性加固策略
核心关键	故障将导致业务中断或SLA严重违规。	实施最高级别冗余（如设备级M-LAG、链路级DPFR）、部署纳秒级加密，并利用AI进行48小时故障预测和毫秒级自动切换。
重要	故障可能导致业务性能下降，但有冗余路径。	确保负载均衡配置最优，并实施快速重路由。监控应关注性能劣化趋势。
一般	故障影响范围局限，业务无感知。	采用标准监控和基础运维流程即可，避免过度投资。

总而言之，"韧性中心性"的实践意义在于，它将网络运维从"被动救火 "转变为"主动防御和精准投资"。通过系统性地量化每一个组件对业务连续性的真实影响，运维团队能够：

一眼看清网络中的"主动脉"和脆弱点。
预先演练故障发生后的场景和应对措施。
精准投入资源，将对业务最重要的组件保护到最高级别。

1.9.3 M-LAG、BGP FRR 等技术与韧性中心性指标的协同工作

实际上构成了一个从 "感知-评估-决策-执行" 的智能韧性闭环。这个闭环系统能主动识别网络中的脆弱点，并自动执行精准的切换动作。

从韧性中心性分析到M-LAG/BGP FRR自动切换的完整闭环流程：

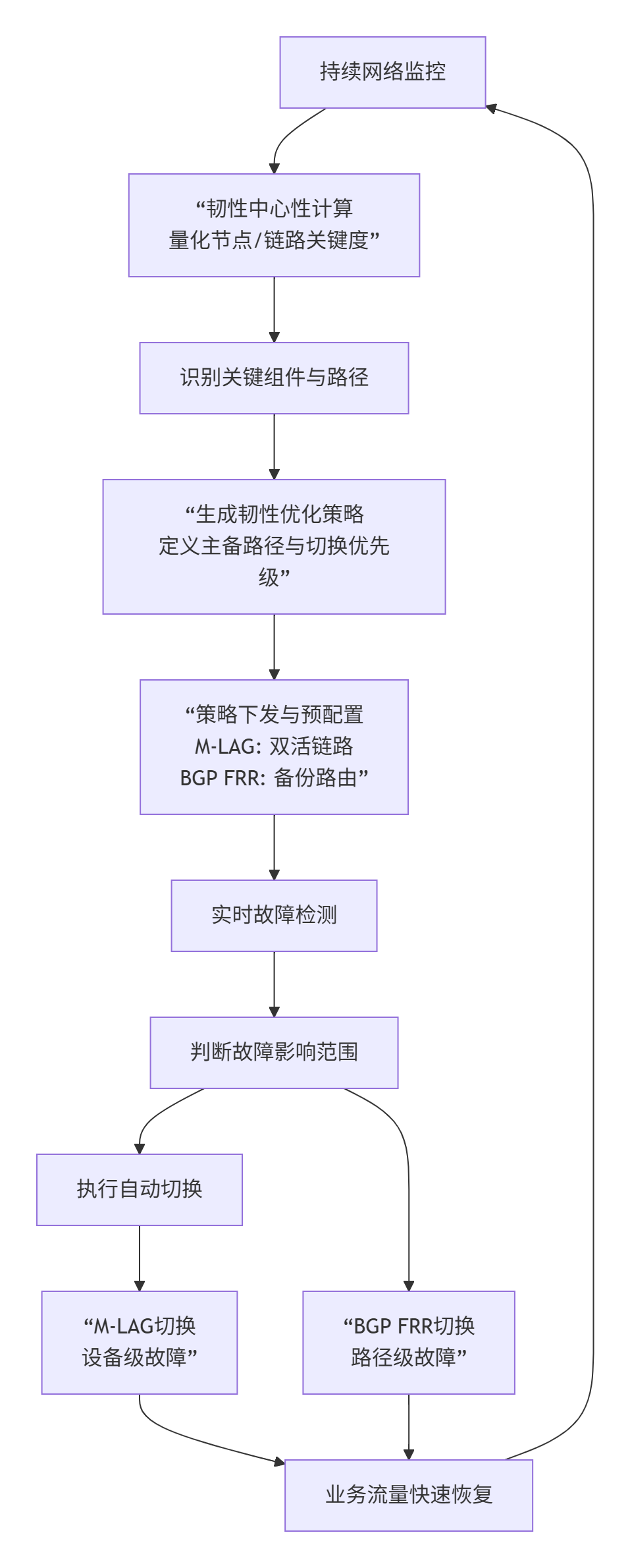
韧性中心性：识别网络"骨架"

韧性中心性的核心价值在于量化网络中每个节点和链路对全局连通性的重要程度。

关键指标 ：它通过分析网络拓扑，计算诸如介数中心性 和紧密中心性等指标。介数中心性高的节点/链路，意味着大量数据流经其上，一旦故障影响范围广；紧密中心性高的节点，则意味着到网络中其他节点的平均距离最短，通常是信息交换的枢纽。
指导意义 ：通过这些计算，运维系统能清晰识别出网络的"主动脉"和"关键枢纽"。例如，计算结果显示某台核心交换机的失效会显著增大网络直径或断开多个子网，其韧性中心性指标就会非常高，标志着它需要被重点保护。

技术协同：M-LAG 与 BGP FRR 的角色

基于韧性中心性分析识别出关键区域后，M-LAG 和 BGP FRR 分别从不同层面提供保护。

技术	保护层级	核心职责	协同点
M-LAG	设备/链路级	解决"单点故障"。通过跨设备链路聚合，使两台物理交换机在逻辑上作为一台设备与上层网络协同工作。当一台设备或一条链路故障时，流量在毫秒级内切换到聚合组内的其他成员链路，保证关键节点的高可用性。	通常部署在韧性中心性高的关键节点（如核心交换机、数据中心网关）的上下游，为其提供设备级的冗余保障。
BGP FRR	路径/网络级	解决"路径故障"。通过预先计算备份路径，当主路径中断时，利用 BFD 等机制快速检测并触发切换，将流量重路由到备份路径，保证端到端的连通性。	为韧性中心性高的关键业务流规划主备路径。确保即使关键路径上的节点或链路中断，业务仍有冗余路径可达。

实现智能闭环的关键步骤

图表中的流程要顺畅运行，依赖于以下几个关键步骤的紧密配合：

策略生成与预配置：控制器根据韧性中心性分析结果，会生成具体的韧性策略。例如："为经过核心交换机A（高韧性中心性）的关键业务流Z，预先通过BGP FRR计算好一条完全绕开A的备份路径。"同时，在交换机A和B上配置M-LAG，确保服务器接入的高可用性。
快速故障检测 ：这是快速切换的前提。BFD 等技术被广泛应用于与M-LAG和FRR联动，能够提供毫秒级的故障检测，为自动切换赢得时间。
智能切换决策与执行：故障发生时，系统并非盲目切换。例如，如果是M-LAG成员链路故障，M-LAG本身即可处理。但如果是整台设备故障或路径中断，系统会结合韧性中心性指标快速评估影响范围：
- 若故障点韧性中心性高，影响重大，则立即触发BGP FRR进行路径级切换。
- 控制器在决策时，会选择韧性中心性最优的备份路径，避免流量被切换到另一个同样脆弱或拥塞的路径上。

1.9.4 动态异构冗余（DHR）架构、AI驱动的韧性原子服务、智能路由（如SD-WAN）

等技术，开始与韧性中心性指标深度结合，推动网络从"快速修复"转向"扰动免疫"。

技术方向	核心理念	如何与韧性中心性协同
动态异构冗余（DHR）	通过构造多个异构的、可动态调度的功能单元，使得网络在面临未知威胁时，能通过策略调度和多元裁决实现"结构免疫"。	韧性中心性指标帮助识别最关键的网络功能或数据流，从而优先为这些高价值目标配置DHR保护。同时，DHR系统的调度器可以利用韧性中心性指标，在多个异构执行体中选择当前最安全、最健壮的路由路径。
AI驱动的韧性原子服务	将网络的自愈能力（检测、抵抗、恢复、演进）拆解为可编排的"原子服务"，并通过AI模型进行智能调度。	韧性中心性指标为AI决策提供关键输入。例如，当AI检测到异常时，可以结合实时计算的韧性中心性图谱，优先对韧性中心性高的关键节点或链路触发"抵抗"或"恢复"原子服务，实现资源精准投放和故障影响的最小化。
智能路由（如SD-WAN）	基于实时网络状态（延迟、抖动、丢包）、应用策略和成本因素，智能选择最优的数据传输路径。	在路径计算中，不仅考虑传统性能指标，也将路径所经过节点的结构性韧性中心性纳入算法。避免使用那些虽然当前性能尚可，但本身结构性脆弱（即韧性中心性低）的路径，从而提升整体路由的鲁棒性。
微服务与云原生韧性	在云原生环境中，通过服务网格、不可变基础设施等技术，实现应用级的快速故障隔离和恢复。	在微服务依赖图中，识别出韧性中心性低的脆弱服务（即其故障容易引发级联雪崩），并对其进行重点加固，如部署重试机制、断路器、故障注入演练等，从而提升整个应用链的韧性。

动态异构冗余（DHR）与内生安全

DHR架构的核心思想是将网络功能或数据转发路径进行异构化，即使某一路径因未知漏洞遭受攻击，其余异构路径仍能保障服务的连续性 。例如，在6G核心网韧性体系中提出的"点-线-面"三维增强机制，其"面"的层面就借鉴了DHR思想，通过异构化来改变业务系统的单一性，从而在面对攻击或故障时能灵活切换，保持业务稳定。韧性中心性指标在这里的作用，是帮助系统精准识别最需要施加这种高级保护的核心资产。

AI与韧性原子服务

这是一种将韧性能力服务化、原子化、并可智能调度的思路。其框架通常包含：

检测原子服务：负责实时监控网络状态。
抵抗原子服务：在遭受攻击时，执行如流量限速、端口禁用等操作，尽力维持业务运行。
恢复原子服务：在故障发生后，执行如节点重启、流量迁移等操作，恢复中断的业务。
演进原子服务：从历史事件中学习，优化未来的防御和响应策略。

AI作为"大脑"，根据全局态势（包括由韧性中心性指标绘制的"网络韧性地图"）来动态编排和调用这些原子服务。例如，当AI通过感知与信念更新模块 发现某个关键节点（高韧性中心性）的流量异常时，可立即联动决策层，优先调度"抵抗"和"恢复"原子服务到该区域，实现精准自愈。

智能路由与资源调度

以SD-WAN为代表的智能路由技术，其核心是实时感知网络状况并为应用选择最佳路径 。现代的SD-WAN解决方案可以与管控编一体的云化平台（如ZENIC ONE）结合，实现对全网链路状态的感知和策略下发。在这个过程中，路径计算算法可以超越传统的成本与性能指标，将路径上网络元素的韧性中心性作为一个重要的权重因子。这意味着，系统会倾向于选择那些由更具韧性（即更不易被摧毁或中断）的节点和链路构成的路径，从而从结构上提升连接的可靠性。

微服务与云原生韧性

在微服务架构中，韧性更多地体现在应用层级 。通过服务网格（Service Mesh）等技术，可以为每个微服务实例注入韧性能力，如超时控制、熔断降级和故障注入。韧性中心性分析在这里可以应用于服务依赖图，找出整个调用链中最薄弱的环节（即韧性中心性低的微服务），并对这些服务进行重点防护和冗余设计，防止因单个服务故障导致整个应用雪崩。

总结与展望

总而言之，网络自愈技术的演进方向是更加智能化、内生化和精细化 。未来的趋势是这些技术协同工作，形成一个闭环：系统持续感知网络状态并计算韧性中心性等指标；AI引擎根据这些指标进行分析决策 ，并调度相应的原子服务；执行层面（如DHR、SD-WAN）精准地完成流量调度或路径切换；最后，整个过程的经验和数据被反馈给学习系统，实现韧性的持续演进。这使网络最终成为一个能够预测、抵御攻击并从攻击中自动恢复的"生命体"。

1.9.5 传统的韧性中心性分析从单云扩展到跨云

在混合云与多云环境中，将传统的韧性中心性分析从单云扩展到跨云层面，确实能帮助我们更精准地评估链路故障对全局业务 的实际影响。其核心在于，不仅要看网络是否连通，更要看中断的链路是否卡住了关键业务的"咽喉"。

单云与混合多云环境下韧性中心性分析的关键差异。

分析维度	传统单云环境	混合云/多云环境（扩展方法）
分析范围	单个数据中心或区域网络内部	跨云链路、跨区域连接、云服务商内部网络
关键指标	节点/链路介数中心性、连通分量	跨云业务流的关键度、云服务商SLA依赖度、跨云延迟与带宽
业务影响评估	相对直接，主要考虑网络路径可用性	引入业务权重，区分核心业务与普通业务；分析业务链路的跨云依赖深度
数据来源	网络设备流量、拓扑数据	全球可观测性平台（日志、指标、链路追踪）、云服务商API （健康状态）、业务链路追踪

构建跨云业务依赖图

这是所有分析的基础。您需要绘制一张清晰的"地图"，标识出所有关键要素：

节点：包括不同云上的虚拟机/容器 、可用区 、特定云服务 （如云数据库实例）、以及关键的跨云网关。
边：代表业务流量实际走过的网络路径。这不仅是云商官方提供的专线，也包括通过公共互联网或SD-WAN建立的连接。

通过全链路追踪技术，可以自动发现并持续更新这张图，准确反映微服务间的动态调用关系和流量比例。

量化链路关键度与业务影响

有了"地图"后，下一步是评估每条"道路"（链路）的重要性。这需要综合计算：

结构性关键度 ：沿用传统网络中心性指标（如介数中心性），计算某条跨云链路位于多少条最短通信路径上。通过的路径越多，其结构性越关键。
业务权重关键度 ：这是扩展分析的精髓。为不同的业务系统（如核心交易、数据分析、后台批处理）分配不同的权重。一条可能只承载少量路径的链路，但如果这些路径全部服务于核心交易系统，那么它的业务关键度就非常高。
云商依赖性：评估链路所依赖的云服务商本身的历史稳定性。如果一条链路完全依赖于一个近期故障频发的云商，那么它的风险等级就需要调高。

综合这些因素，可以为每条跨云链路计算一个综合韧性得分。这样，您就能一目了然地识别出，哪些链路的故障会对全局业务造成致命打击。

主要实施路径与技术策略

将理论付诸实践，需要一套清晰的技术路线和工具作为支撑。

统一可观测性平台 ：这是成功的基石。需要建立一个平台，能够从所有云环境、本地数据中心和网络设备中采集、关联并统一存储指标、日志和链路追踪数据。京东云的实践表明，统一的视角对于实现有效的多云管理和调度至关重要。
动态权重与SLA集成 ：业务权重不应是静态的。它可以与业务系统的实时SLA（服务等级协议）挂钩。当某个业务的重要性在特定时间窗口（如电商大促）升高时，其依赖链路的权重也应动态调整，从而实现更精准的影响评估。
韧性策略与闭环控制：分析的最终目的是指导行动。基于韧性中心性分析的结果，可以制定和优化具体的韧性策略。
- 路径优化：为关键业务配置多条独立的跨云路径，避免单一故障点。
- 智能调度：在跨云链路中断时，能够根据预设策略，自动将关键业务流量切换到健康的路径上。
- 容量规划：识别出结构性关键的单点链路后，可以有针对性地进行扩容，提升整体冗余。

总结与核心价值

总而言之，在混合云/多云环境中扩展韧性中心性分析，意味着从"网络连通性"视角转向"业务影响力 "视角。它通过构建统一的业务依赖图 ，并综合结构性指标 和动态业务权重。

1.9.6 多云环境中精准调整业务系统的权重

在多云环境中，精准调整业务系统的权重是一项核心工作，它能确保资源总是优先保障最关键的业务。

调整维度	核心目标	关键监控指标/数据源	动态调整策略示例
业务价值与SLA	使权重与业务的收入贡献和服务等级协议直接挂钩。	实时交易额、用户活跃度、SLA合规率（如错误率、延迟）。	电商大促期间，订单核心链路的权重自动提升；SLA即将违约时，系统自动为其分配更多资源。
实时性能与健康度	根据应用的当前运行状态动态分配资源，避免瓶颈。	应用性能监控（APM）数据：P99延迟、QPS、错误率；基础架构健康度。	某业务API延迟飙升时，临时调高其权重以获取更多计算资源；实例不健康时权重降为零。
资源利用率与成本	优化资源使用效率，实现成本效益最大化。	CPU/内存/网络利用率、云服务费用账单。	识别并调低资源消耗高但业务价值低的任务的权重；设置预算阈值，触发时优先保障高价值业务。
依赖关系与拓扑	反映业务在全局依赖图中的关键程度，避免级联故障。	业务依赖图、关键路径分析、上下游健康状况。	某个被大量核心业务依赖的底层认证服务，其权重应始终保持在高位。

如何实施动态调整

在实际操作中，动态调整是一个持续优化的闭环过程，其核心是 **"感知-决策-执行"** 的自动化循环。

建立统一的度量与采集体系

这是所有决策的基础。你需要建立一个统一的可观测性平台，能够采集来自业务、应用和基础设施的各类指标。这包括：
- 业务指标：如订单量、交易额、活跃用户数等，通常通过数据总线和日志收集。
- 应用性能指标：如服务的P99延迟、QPS、错误率，通过APM工具获取。
- 资源指标：如CPU、内存、网络I/O使用率，由云平台的监控系统或Prometheus等工具提供。
- 依赖拓扑数据：通过分布式链路追踪（如SkyWalking, Jaeger）自动生成实时的服务依赖图。
设计权重计算模型

这是一个综合决策过程，可以将上述多维指标输入一个权重计算引擎。这个引擎可以设计为一个加权公式，例如：

最终权重 = (业务价值系数 × SLA健康分) + 性能紧迫系数 + 成本优化系数 - 依赖风险系数

其中，每个系数都是一个根据实时数据计算出的动态值。更先进的方案会采用机器学习模型，根据历史数据学习不同情况下各指标的最优权重组合，实现更精准的预测性调整。
实现自动化策略执行

计算出的新权重需要被自动执行。这通常通过与调度系统（如Kubernetes）、服务网格（如Istio）和云管平台（CMP）的API集成来实现。例如：
- 当计算出一个业务的新权重后，调度器可以动态调整其Pod的副本数或资源限制。
- 在服务网格中，可以动态修改路由规则，将更高比例的流量分发给权重更高的服务实例。
- 通过事件驱动架构，当监控到特定事件（如SLA即将违约）时，自动触发预定义的权重调整策略。

实践要点与挑战

避免权重振荡 ：为防止权重因指标微小波动而频繁变化，需要引入迟滞机制。例如，只有当性能指标持续偏离阈值一段时间后，才触发权重调整。
权重标准化：确保所有权重最终能归一化到一个可操作的范围内（如0-100），以便调度器理解。
灰度与回滚：任何权重调整都应遵循灰度原则，先在小范围生效，验证无误后再全量推开，并配备一键回滚机制。
平衡自动化与人工干预：虽然追求自动化，但对于核心业务权重的重大调整，系统应能发出警报，供运维人员最终确认。

动态调整业务权重的本质，是将业务意图（价值、SLA）与系统实时状态（性能、健康度）通过数据驱动的方式，翻译成资源调度系统能理解的指令。这需要一个集监控、分析、决策、执行于一体的自动化平台作为支撑。

1.9.7 多个高权重业务同时争夺有限资源的优先级仲裁机制

在多云环境中，当多个高权重业务同时争夺有限资源时，一个科学、公平且高效的优先级仲裁机制至关重要。这不仅能确保关键业务不受影响，还能提升整个资源池的利用效率。下面的表格梳理了构建这套仲裁机制时可以综合考虑的核心维度。

仲裁维度	核心目标	关键方法与机制
业务价值量化	将业务重要性转化为可比较的数值指标。	综合SLA等级、实时收益影响、战略重要性等因素，为每个业务计算静态基础权重。
系统状态感知	让决策贴合系统实时健康状况，避免雪崩。	引入动态权重调整，基于资源利用率、服务健康度、排队等待时间等实时指标进行奖惩。
竞争解决策略	在基础权重相近时，提供公平且高效的决胜规则。	采用加权轮转、最大最小公平算法，或参考双向竞拍中的交易延时排队影响因子，对等待久的请求给予适当优先。
执行与自愈	确保仲裁决定能有效执行，并在故障时能平滑恢复。	利用优先级抢占，并设置优雅的驱逐策略；同时通过智能合约或预定工作流实现自动故障转移和重调度。

如何设计仲裁机制

设计仲裁机制时，可以结合以下几种策略，结合静态与动态因素，实现一个多层次、自适应的智能调度系统。

基于加权优先级的综合评判

这是最核心的一步。系统不应只根据业务的"重要级别"，而应计算一个综合权重分数。这个分数可以静态与动态相结合：
- 静态部分：根据业务的SLA等级（如白金、金、银）、每小时产生的实时收益、以及企业的长期战略价值（如核心数据同步业务）来确定一个基础权重。
- 动态部分 ：引入动态调整因子。例如，某个业务的资源利用率已持续高位运行，其当前请求的权重应被适当调高，以防过载；反之，一个健康度开始下降的业务，其新任务的权重可被暂时调低，避免给不稳定的实例雪上加霜。这种机制在Kubernetes的优先级抢占调度中已有体现，调度器会综合考量Pod的优先级和节点状态。
引入市场机制与博弈论

当多个来自不同租户的高权重业务僵持不下时，可以引入双向竞拍 等市场机制。云资源提供商和业务方（或代表业务的调度器）分别提交要价和报价。一个公正的"拍卖师"（调度仲裁器）根据双方的出价、资源量以及类似交易延时排队影响因子等参数进行匹配。这能将资源分配转化为一个寻求整体利益最大化的优化问题，并通过算法（如寻找贝叶斯纳什均衡解）得出相对最优解。
利用智能合约实现自动化与可信仲裁

为了确保仲裁规则的透明和不可篡改，可以将优先级规则、抢占条件、补偿策略等编码成智能合约并部署在区块链上。一旦满足触发条件（如资源阈值、权重分数差），合约将自动执行仲裁决策，进行资源调配。这种方式减少了人为干预，增加了各方对调度结果的信任度，特别适用于多租户场景。

解决冲突与保证公平

在权重分数非常接近或机制需要决出最终胜者时，以下策略有助于做出公平决策：

决胜局规则 ：可以优先选择等待时间更长 的业务请求，类似双向竞拍中为等待轮次多的交易赋予更高优先级。也可以参考Kubernetes的策略，优先选择那些抢占成本更低的节点（例如，其上运行的待抢占Pod优先级更低、数量更少）。
保证基本公平 ：为避免低优先级业务被"饿死"，可以引入最大最小公平算法 之类的思想，确保所有业务都能获得最低限度的资源保障。同时，设立抢占代价补偿机制，对于被抢占的资源，系统应记录并在后续资源空闲时优先补偿给该业务，或给予费用折扣。

执行阶段与稳定性保障

仲裁决策后，需要稳妥地执行资源调配，并确保系统稳定。

优雅抢占与故障转移 ：执行抢占时，应通知被抢占方并给予其优雅终止 的时间。同时，调度系统必须确保高优先级业务在抢占后能成功运行，并具备自动故障转移的能力，防止资源腾出后业务仍无法启动的尴尬局面。
持续监控与动态调整 ：仲裁机制不是一成不变的。需要持续监控仲裁决策的实际效果，根据系统整体运行情况和业务反馈，动态调整权重计算模型和仲裁参数，实现机制的持续优化。

总结与展望

面对多云环境下高权重业务的资源竞争，一个优秀的优先级仲裁机制必然是多维度、自适应、且自动化的。它需要将业务价值、系统实时状态、市场规则与自动化技术相结合。

在多云环境中，要确保仲裁机制既公平又高效，需要一套清晰的验证框架和关键指标。

验证维度	核心目标	关键方法与技术
公平性验证	确保资源分配不偏不倚，策略执行透明可信。	智能合约审计、博弈论分析（如纳什均衡）、区块链存证与跨云成本/性能对比。
效率验证	确保资源调度快速精准，系统响应及时。	模拟负载测试、真实环境监控（追踪API响应时间、任务排队时长等）、数据一致性审计。
持续监控与调优	建立闭环，使机制能够持续改进。	建立性能基线、设置动态阈值告警、定期复盘评审。

如何验证公平性与效率

公平性和效率需要具体的验证手段。

公平性验证 ：关键在于可追溯的透明性 和无偏见的分配结果。
- 审计与透明度 ：利用区块链技术 记录每次仲裁决策的完整日志，确保过程不可篡改、可审计。决策逻辑（如资源分配算法）最好通过智能合约实现，其代码开源或可被审查，能有效提升各方信任度。
- 结果分析 ：可以通过回溯分析 ，检查在相似负载和优先级条件下，不同用户或业务部门的资源分配结果是否一致。利用博弈论模型 （如分析是否达到或接近纳什均衡）来评估是否有用户可以通过策略性行为（如虚假申报资源需求）获取不当优势。同时，比较不同云厂商资源的实际性能与成本是否与仲裁策略的预期相符。
效率验证 ：侧重于速度和资源利用度。
- 模拟与压力测试 ：在隔离环境中，使用模拟工具生成接近极限的并发资源请求，测试仲裁引擎的吞吐量 和决策延迟 。同时，检查在高负载下，仲裁决策的错误率 或冲突发生率是否在可接受范围内。
- 真实环境监控 ：在线上环境中，密切监控API响应时间 、资源分配任务在队列中的平均等待时间 ，以及从仲裁决策下达到云平台完成资源部署的端到端时间 。此外，还需审计跨云数据同步的一致性延迟，确保仲裁决策依赖的数据状态是准确的。

需要关注哪些关键指标

验证工作需要具体的数据指标支撑，它们是你评估系统状态的"仪表盘"。

效率核心指标：
- 仲裁决策延迟：仲裁引擎处理一个资源请求并做出决策所需的时间。此值越低，用户体验越好。
- 资源分配成功率：在指定时间内（如SLA要求）成功完成资源调配的请求比例。这是衡量可靠性的直接指标。
- 资源利用率：仲裁分配出去的CPU、内存、存储等资源被实际使用的平均比率。避免资源闲置是提升效率、控制成本的关键。
公平性核心指标：
- 用户满意度：通过调研或系统反馈渠道收集不同用户组对资源分配公平性的主观评分。这提供了重要的定性参考。
- 策略违规次数：监控并统计违反既定仲裁策略（如优先级规则、配额制度）的事件发生次数。
- 跨云成本效益比：比较在不同云厂商上执行相同任务的实际成本与性能输出，确保仲裁决策在成本控制上是有效的。
系统可靠性指标：
- 服务可用性：仲裁服务本身的可访问性，通常用多个9（如99.9%）来衡量。
- 故障恢复时间：当仲裁服务或依赖的组件出现故障时，系统恢复到正常状态所需的平均时间。

如何实施调优

验证和度量之后，更重要的是根据发现的问题进行持续调优。

建立基线与目标 ：首先通过一段时间的监控，了解各项关键指标在当前系统中的正常波动范围，建立性能基线 。然后，与业务方共同设定明确的、可衡量的优化目标（例如：将仲裁延迟从500毫秒降低到200毫秒）。
实施更改与监控 ：基于假设进行优化，例如调整仲裁算法的参数、引入新的调度策略或升级硬件资源。每次只变更一个变量，并密切监控变更后指标的变化，与基线进行对比。
复盘与迭代：定期召开复盘会议，分析调优措施是否达到预期目标，总结经验教训，并规划下一轮的优化周期。这是一个持续改进的循环过程。

重要原则

验证和调优多云仲裁机制是一个持续的过程。关键在于建立可量化的指标、实现高透明度和可观测性，并嵌入持续改进的闭环文化。

1.9.8 基础设施韧性到业务韧性的映射模型与权重分配

将基础设施的"物理健康度"转化为业务的"功能健康度"，关键在于建立一套科学的量化桥梁。

核心数学模型与框架
- PSR（压力-状态-响应）模型 ：这是一个非常经典且实用的框架。在评估城市基础设施韧性时，将指标分为压力（如极端天气、高人口密度）、状态（如燃气普及率、道路密度）和响应（如预警能力、恢复投资）三个维度。业务韧性可以视为这些基础设施维度共同作用的最终输出。您可以建立统计模型（如多元回归）或机器学习模型，以基础设施的PSR指标为自变量，以业务指标（如订单成功率、系统吞吐量）为因变量，拟合出映射关系。
- 云模型 ：当评价中存在大量模糊性和随机性时，云模型是绝佳工具。它能实现定性概念（如"韧性良好"）与定量数值之间的自然转换。在评估洪涝灾害下地铁站点或装配式建筑供应链节点的韧性时，该模型通过期望值、熵和超熵三个数字来表征一个定性概念，从而更科学地处理专家判断中的不确定性，使综合评价结果更稳健。
- 解释结构模型（ISM）：对于复杂系统，的研究表明，ISM能帮助厘清众多影响因素之间的层级结构和内在逻辑关系。您可以先用ISM找出影响业务韧性的关键基础设施变量，从而简化映射模型，聚焦于驱动能力最强的少数核心基础设施指标。
权重分配的最佳实践
- 主客观组合赋权：这是当前公认的最佳实践，旨在平衡专家经验与数据客观性。
  - 主观赋权 （如AHP层次分析法）：利用专家知识判断各指标相对重要性。这能确保权重贴合业务战略，但可能受主观偏见影响。
  - 客观赋权 （如熵权法）：根据指标数据本身的离散程度自动分配权重。数据波动性大的指标，其熵权通常更高。这能敏锐捕捉到变化剧烈的因素，但可能偏离业务逻辑。
  - 组合赋权：将AHP得到的主观权重与熵权法得到的客观权重进行组合（如基于博弈论或最小二乘法寻优），得到综合权重。这种方法在和的研究中都得到了成功应用，兼顾了"业务价值"和"数据波动"。
- 验证性因子分析（CFA）：在拥有大量数据的情况下，可以像中研究民航基础设施那样，采用CFA等统计方法验证指标体系的结构效度，并利用其因子载荷等结果辅助确定权重，确保权重分配的科学性。

韧性中心性计算的复杂度与精度平衡策略

直接计算大规模复杂网络的精确韧性中心性（通常涉及复杂图论算法和大量仿真）可能计算成本极高。平衡计算复杂度与评估精度是一门艺术，核心思想是 "用适当的近似，换足够的洞察"。

实用近似算法与简化策略
- 基于物理的简化模型 ：在工程领域，采用简化物理模型替代精细的完全仿真是一种常见策略。例如，的研究表明，在评估RC框架建筑的隔震韧性时，采用基于铁木辛柯梁理论的组合简化模型（HST），在保证关键响应（如楼面加速度）预测精度的同时，计算效率远高于复杂的精细有限元模型。这种思想可以借鉴到网络分析中，例如，用超点或社区结构来近似表示一个密集连接的子网，从而降低网络规模。
- 反向有限元法与参数反演 ：对于特定参数的标定，采用遗传算法、随机游走算法等优化算法进行反向有限元分析。通过少量试验或监控数据，反向推演出关键材料参数（如内聚力模型参数）。这避免了全参数空间的暴力搜索，大幅降低了计算成本。在网络中，可以类比为通过有限的压力测试数据，来校准一个简化的网络性能模型。
- 敏感度分析驱动的简化：在建模前进行敏感度分析，识别出对最终韧性中心性影响最大的网络属性和故障场景。的研究就通过分析几何尺寸对参数敏感性的影响，优化了试样设计。集中计算资源于这些高敏感度区域，忽略次要因素，可以有效平衡计算开销。
平衡之道：分层评估与自适应计算
- 分层评估 ：不要试图一次算遍全网。可以先进行粗粒度评估 ，快速识别出网络中的关键区域（例如，通过度中心性、介数中心性等简单指标进行初筛）。然后，再对这些关键子系统进行细粒度的韧性中心性深度分析。
- 增量/自适应计算 ：对于动态变化的网络，若非拓扑巨变，可采用增量计算思路。即主要重新计算变化区域及其受影响的部分，而非每次都推倒重来，这能显著提升效率。

核心总结

总而言之，将基础设施韧性映射到业务韧性，最佳实践是采用PSR、云模型等框架 ，并结合主客观组合赋权 来建立量化关系。而在计算韧性中心性时，则应通过物理简化、智能反演、敏感度分析 等近似算法，以及分层评估策略，在可接受的计算成本内获取足够精确的洞察。

1.9.9 云模型的核心组件与实现方法

云模型由期望（Ex） 、熵（En） 和**超熵（He）** 三个参数定义：

Ex：定性概念在论域中的中心值，代表最典型的样本。
En：综合衡量概念的模糊性与随机性，值越大表示概念越宏观或不确定性越高。
He：反映熵自身的波动程度，值越大说明云的离散性越强。

1. 具体实现方法

云模型的实现依赖云发生器，分为正向与逆向两类：

正向云发生器：从定性概念（参数Ex、En、He）生成定量云滴。例如，一维正态云的生成步骤：
1. 生成随机数 En′∼N(En,He2)。
2. 生成云滴值 x∼N(Ex,En′2)。
3. 计算隶属度 μ=exp(−2En′2(x−Ex)2)。
4. 重复以上步骤生成N个云滴。
逆向云发生器：从定量数据（云滴样本）反推参数。例如：
1. 计算数据均值 Ex=n1∑xi。
2. 计算熵 En=2π×n1∑∣xi−Ex∣。
3. 计算超熵 He=S2−En2，其中 S2为样本方差。

代码简例（Python）：

复制代码

import numpy as np
def forward_cloud(Ex, En, He, n_drops):
    drops = []
    for _ in range(n_drops):
        En_prime = np.random.normal(En, He)
        x = np.random.normal(Ex, abs(En_prime))
        mu = np.exp(-(x - Ex)**2 / (2 * En_prime**2))
        drops.append((x, mu))
    return drops

2. 评估算法与参数反演

云模型常用于多属性综合评估，其流程包括：

指标权重分配：结合AHP或熵权法确定权重，减少主观偏差。
综合云计算：加权聚合各指标云模型。例如，顶层云参数计算为：
复制代码
```
Ex综合=∑wiExi,En综合=∑wiEni,He综合=∑wiHei
```
结果比对：将综合云与标准云（如"优秀""良好"对应云）比较，通过相似度或重叠面积判定等级。

3. 物理拓扑简化与敏感度分析

在点云或网络拓扑中，云模型可与拓扑特征提取结合：

拓扑简化方法 ：基于Morse理论识别关键特征线（如脊线、谷线），通过持续值过滤伪特征。例如：
- 计算特征线上点的函数值（如曲率），保留持续值大的特征。
- 使用同态收缩算法合并冗余拓扑结构，提升计算效率。
敏感度分析：通过扰动云模型参数（如He），观察输出云滴分布的变化，评估系统稳健性。例如，超熵He增大时，云层变厚，显示系统对随机性更敏感。

4. 智能反演与中心性指标整合

智能反演：结合模糊逻辑或优化算法（如遗传算法）从数据中反演参数。例如：
- 三角直觉模糊云模型将专家评价（支持度u、反对度v）转换为云参数：
  复制代码
```
Ex=4a+2b+c,En=6(c−a)+(b−a)(u−v),He=6(1−u−v)(c−a)
```
  其中(a,b,c)为三角模糊数。
与中心性指标结合：在网络分析中，度中心性/介数中心性可转换为云模型参数：
- 将节点中心性作为输入，生成表征网络连通性不确定性的云模型。
- 例如，高频节点的Ex较高，En和He可反映中心性值的波动性。

关键应用场景

系统效能评估：如炮兵目标保障能力评估，通过云模型量化模糊指标（如"情报获取能力"）。
拓扑特征保护：在三维点云处理中，简化拓扑同时保留过渡特征。
多专家决策：三角直觉模糊云模型聚合冲突意见，输出带不确定性评估的综合云。

通过上述方法，云模型能有效处理不确定性，实现定性到定量的双向转换，适用于复杂系统的评估与优化。

1.9.10 云模型与网络中心性指标

将云模型与网络中心性指标结合，核心在于利用云模型处理不确定性的优势，对传统确定性中心性指标进行"软化"和"情境化"修正，从而更精细地反映节点的重要性差异。下面这个表格梳理了结合过程中的关键步骤与核心考量，希望能帮助您快速把握全貌。

关键步骤	核心任务	云模型的关键作用与权重分配策略
1. 指标选择与预处理	选取多维度中心性指标，并进行数据标准化。	云模型在此步骤主要为指导指标选择提供不确定性视角，关注那些易受网络微观变动影响的指标。
2. 云转换与参数计算	将每个节点的每个中心性指标值转换为一个云滴，并计算其数字特征（Ex, En, He）。	核心步骤。将确定的指标值转换为（Ex, En, He）三元组。其中，期望（Ex）直接反映该节点在此指标上的"平均水平"；熵（En）表征该指标值的波动性或模糊性；超熵（He）描述熵本身的稳定性。
3. 节点重要性云合成	将同一节点的多个中心性指标云合成为一个综合的"节点重要性云"。	这是权重分配的关键。采用主观权重（如AHP）与客观权重（如熵权法）相结合的方法。云模型的优势在于，它不仅能合成数值（Ex），还能合成不确定性（En和He），使综合结果自带置信度信息。
4. 节点重要性比较与决策	基于合成云进行节点重要性排序。	利用云发生器进行云滴生成，通过比较云滴的整体分布或特定特征（如期望Ex）来进行排序。正向云发生器在此环节发挥作用，将综合云模型转换为大量云滴，便于可视化和概率性解释。

指标选择与云转换

首先，需要选择一组能够从不同维度（局部、全局、媒介能力等）刻画节点重要性的中心性指标，例如度中心性、介数中心性、接近中心性等。随后，将这些指标的原始值进行标准化处理，消除量纲影响。

接着是核心步骤：云转换。为每个节点在某个指标上的表现，定义一个云模型。这个云模型由三个数字特征参数确定：

期望（Ex） ：这通常是该节点在此项指标上的标准化后的值。它代表了该节点在此指标上的"重心"或平均水平。
熵（En） ：熵是不确定性的度量。它可以基于网络拓扑的微观不确定性（如连边的随机性）或节点指标值的历史波动情况进行计算。熵越大，表明该节点此项指标的值越模糊、越不稳定。
超熵（He） ：超熵是熵的熵 ，衡量的是熵本身的不确定性。它反映了熵的波动程度，即节点重要性评估的总体可靠程度。超熵越大，说明评估结果的不确定性越高。

通过这一步，每个节点在每个中心性指标上，都从一个单一数值变为了一个包含中心趋势和不确定性信息的云模型。

权重分配与云合成

得到各指标的云模型后，需要将它们合成为一个代表节点综合重要性的"节点重要性云"。此处的关键在于权重的分配。

主观与客观权重结合：最有效的策略是结合主观赋权法（如AHP）和客观赋权法（如熵权法）。
- **层次分析法（AHP）** 能融入领域专家对各项指标相对重要性的判断。
- 熵权法则根据各指标数据本身的离散程度（变异程度）来分配权重。数据波动性越大（提供信息越多），其熵权通常越高。
- 之后，可以运用线性组合 或更为精细的云模型合成算法，将主客观权重结合，得到每个指标的综合权重。
云模型的加权合成 ：在合成时，不仅合成指标的期望（Ex），更重要的是同步合成熵（En）和超熵（He） 。这使得最终得到的"节点重要性云"不仅包含了综合重要性的期望值，还包含了此次评估的整体置信度。一个熵和超熵较大的节点，即便其重要性期望值很高，也需要谨慎对待，因为评估结果本身的不确定性较高。

比较决策与优势总结

合成得到每个节点的"重要性云"后，如何比较和排序呢？

云滴生成与比较 ：可以利用正向云发生器 ，依据每个节点的综合云模型（Ex_total, En_total, He_total）生成大量云滴。通过比较这些云滴的分布（例如，通过可视化观察云图的相对位置，或计算一个云在另一个云之上的概率），可以对节点重要性进行概率性的排序。在某些要求不高的情况下，也可以直接比较各节点综合云的期望值（Ex_total）进行粗略排序。
方法优势：这种结合策略的优势非常明显：
- 更丰富的表征：从单一数值变为一个概率分布，能同时表达"有多重要"和"评估有多确定"。
- 更强的抗干扰能力：对原始数据中的噪声和波动不敏感，结果更稳健。
- 支持风险感知的决策：决策者能清晰看到评估的不确定性，从而做出更审慎的决策。例如，在两个节点Ex_total相近时，优先保护En_total和He_total更小的那个（即评估结果更确定的节点）可能是更稳妥的选择。

实例说明

假设在一个网络中，我们用度中心性和介数中心性两个指标来评估节点重要性。

节点A：度中心性很高且稳定（Ex高，En低），但介数中心性很低（Ex低，En低）。若网络更看重连接广度（赋予度中心性高权重），其综合重要性会很高。
节点B：度中心性一般但波动大（Ex中，En高），介数中心性很高但受特定路径影响大（Ex高，En中）。若网络更看重控制能力（赋予介数中心性高权重），且考虑不确定性，其综合重要性可能很高但置信度较低。

云模型帮助我们在权重分配和合成过程中，量化并传递了这种不确定性，使得评估结果更具指导意义。