递归
1.什么是递归
就是函数自己调用自己
2.为什么使用递归
本质 主问题 -> 相同子问题 -> 相同子问题
就是解决一个主问题和解决一个子问题一样的思路
3.如何写好一个递归
先找到相同的子问题
只关心这一个子问题如何解决(宏观角度看待问题)
注意递归的出口(结束条件)
搜索 、深度优先遍历、深度优先搜索、宽度优先遍历、宽度优先搜索、暴搜
1.深度优先遍历 VS 深度优先搜索(dfs)
宽度优先遍历VS宽度优先搜索(bfs)
这里遍历是形式,目的是搜索出结果,通过遍历搜索出结果
搜索本质就是暴力枚举一遍所有情况(分为dfs和bfs)
回溯与剪枝
回溯其实本质就是深搜剪枝是截取掉肯定不符合结果的搜索,像走迷宫有条路走不通就将这一条路剪掉
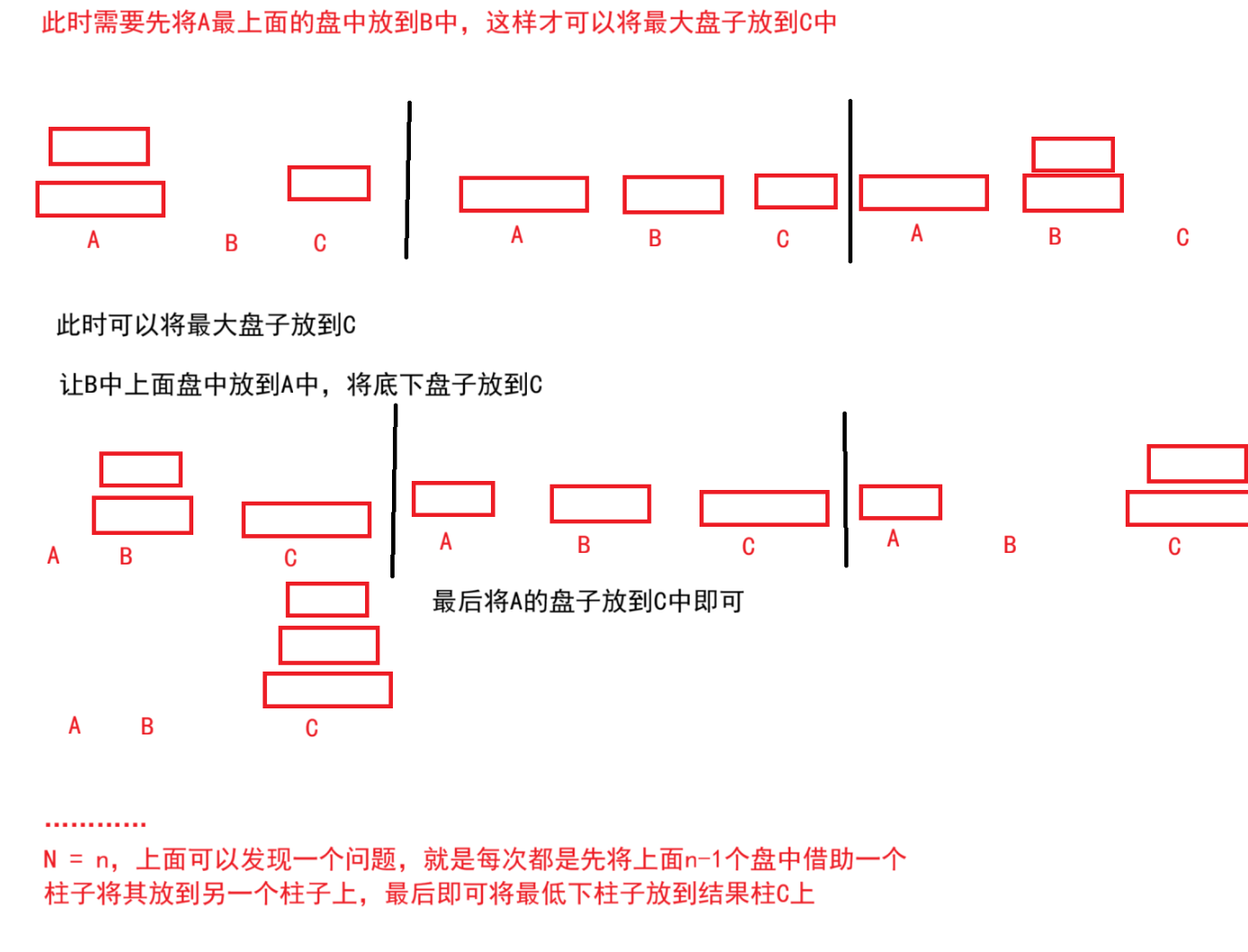
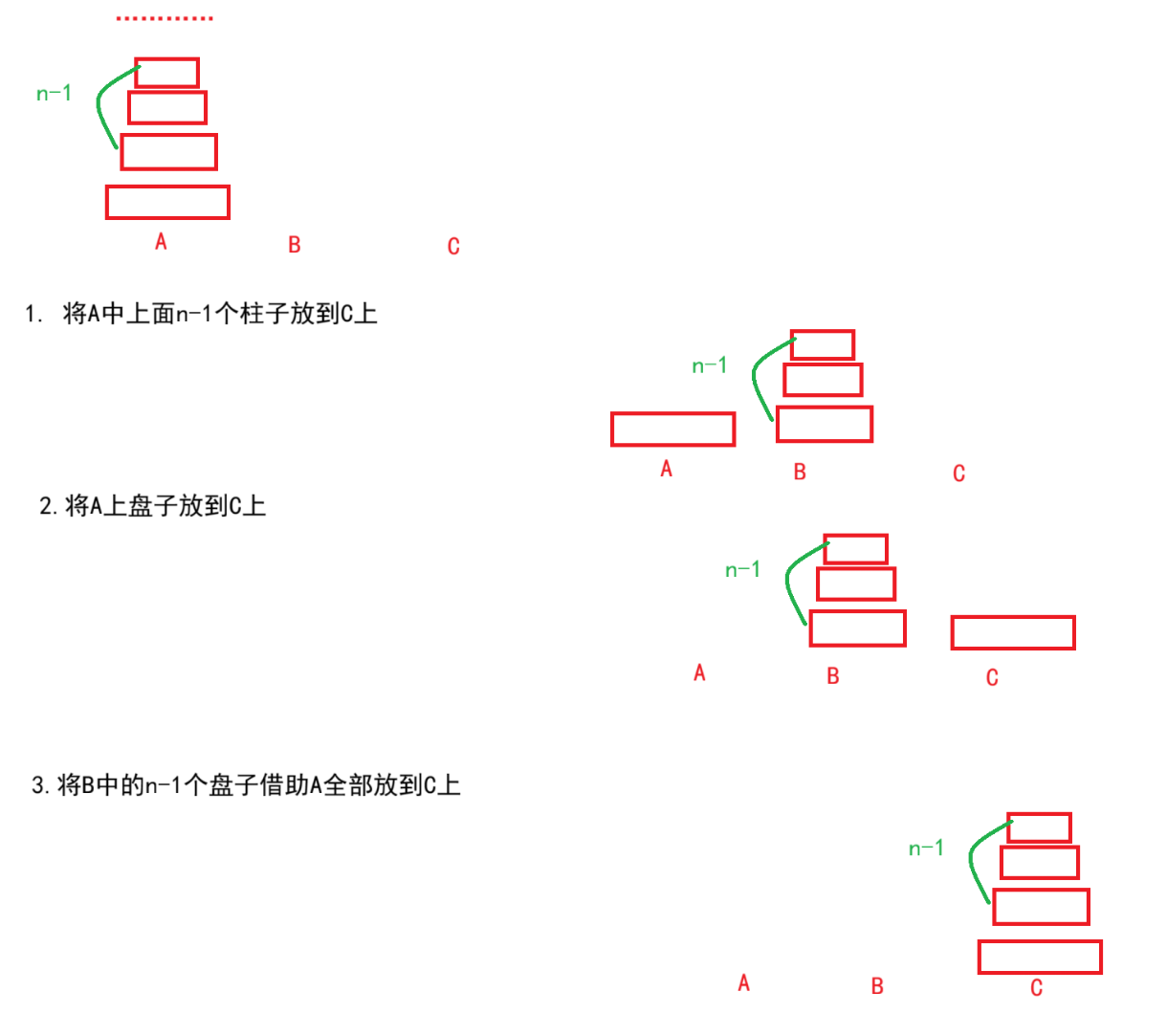
汉诺塔问题

题目解析:就是将A柱子中盘子放到C柱子上

java
class Solution {
public void hanota(List<Integer> A, List<Integer> B, List<Integer> C) {
dfs(A,B,C,A.size());
}
public void dfs(List<Integer> A , List<Integer> B,List<Integer> C,int n){
if(n == 1){
//放盘子
C.add(A.remove(A.size() - 1));
return;
}
dfs(A,C,B,n-1);
C.add(A.remove(A.size() - 1));
dfs(B,A,C,n-1);
}
}合并两个有序链表
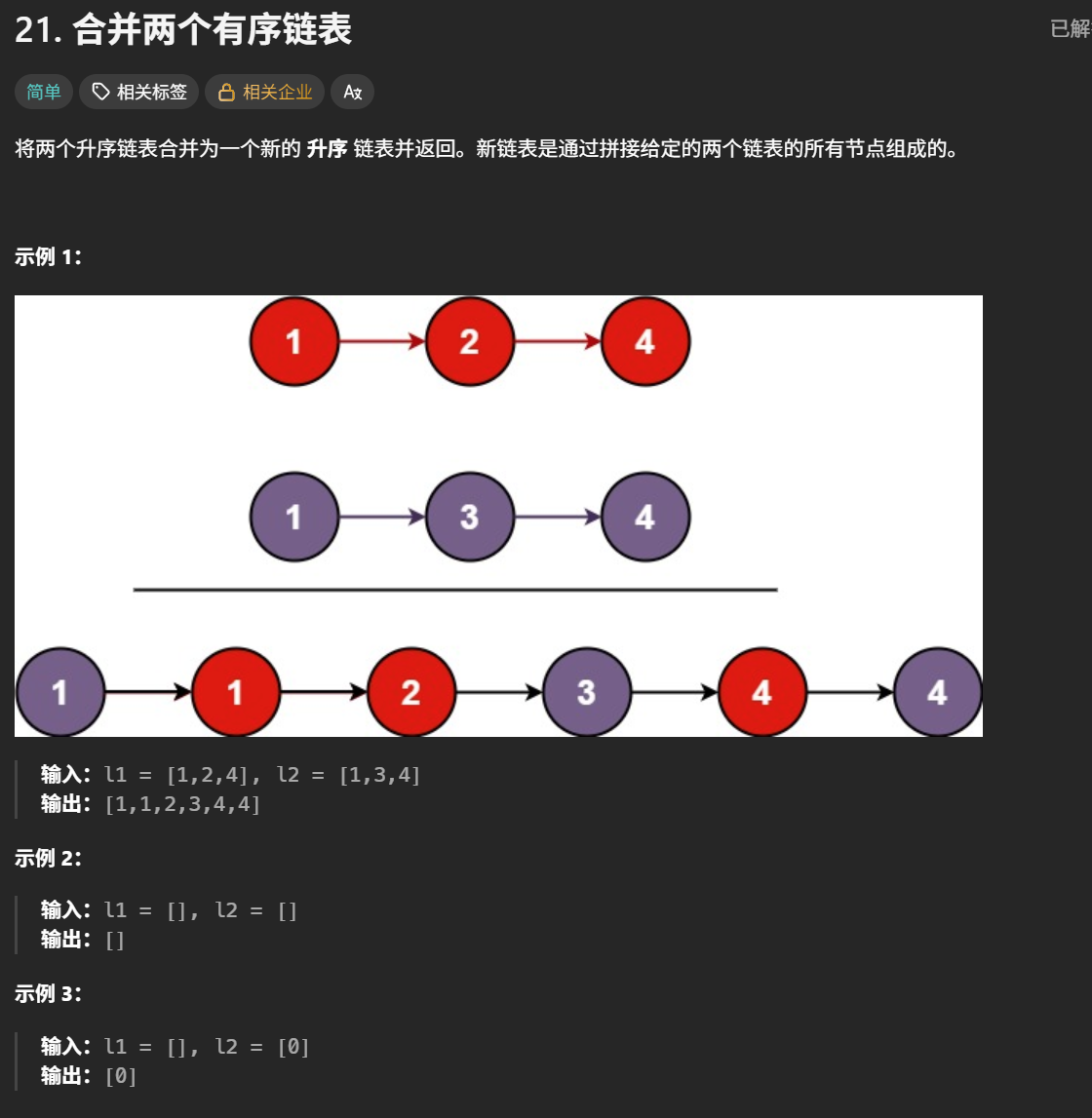
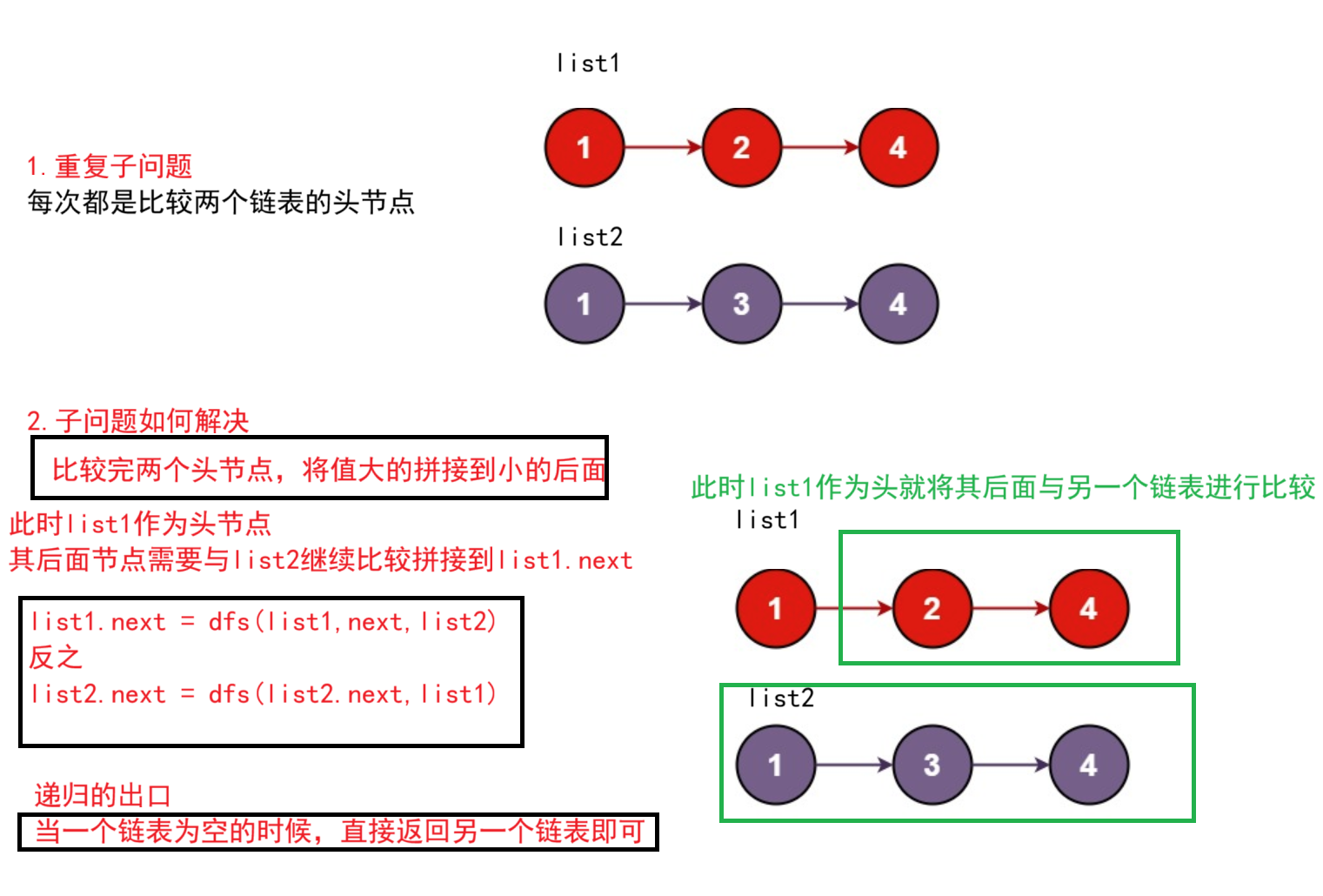
题目解析 :就是就是将两个链表进行合并,并且合并结果中的节点都是这两个链表中的
思想:递归可以简单发现每次都是比较两个链表的头节点的val,那个小就拼接后面,因此如果此时 list1.val < list2.val list1.next = dfs(list1.next,list2)即可另一个同理
java
class Solution {
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
//递归
//子问题比较两个链表头节点
if(list1 == null){
return list2;
}
if(list2 == null){
return list1;
}
if(list1.val <= list2.val){
list1.next = mergeTwoLists(list1.next,list2);
return list1;
}else{
list2.next = mergeTwoLists(list2.next,list1);
return list2;
}
}
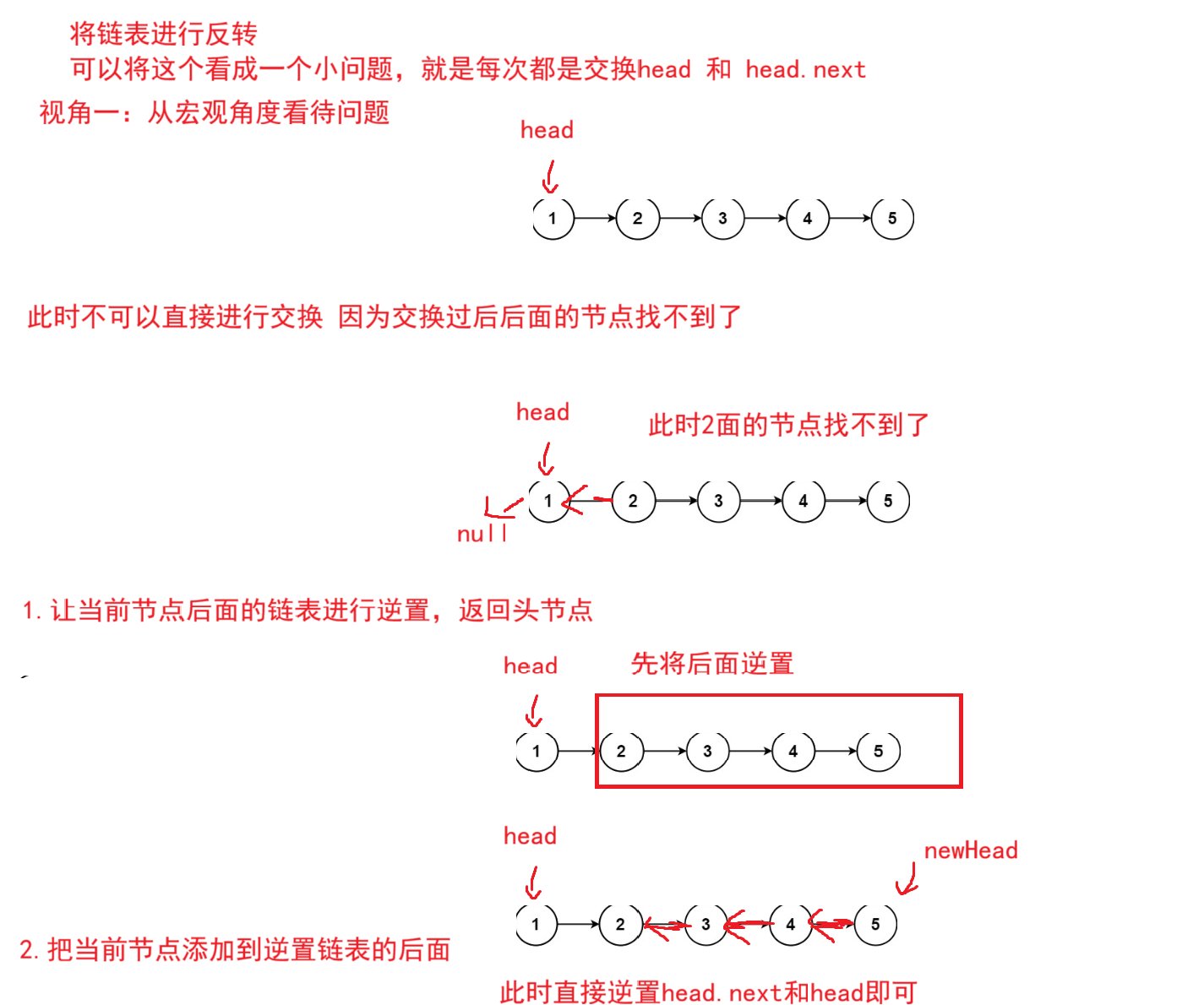
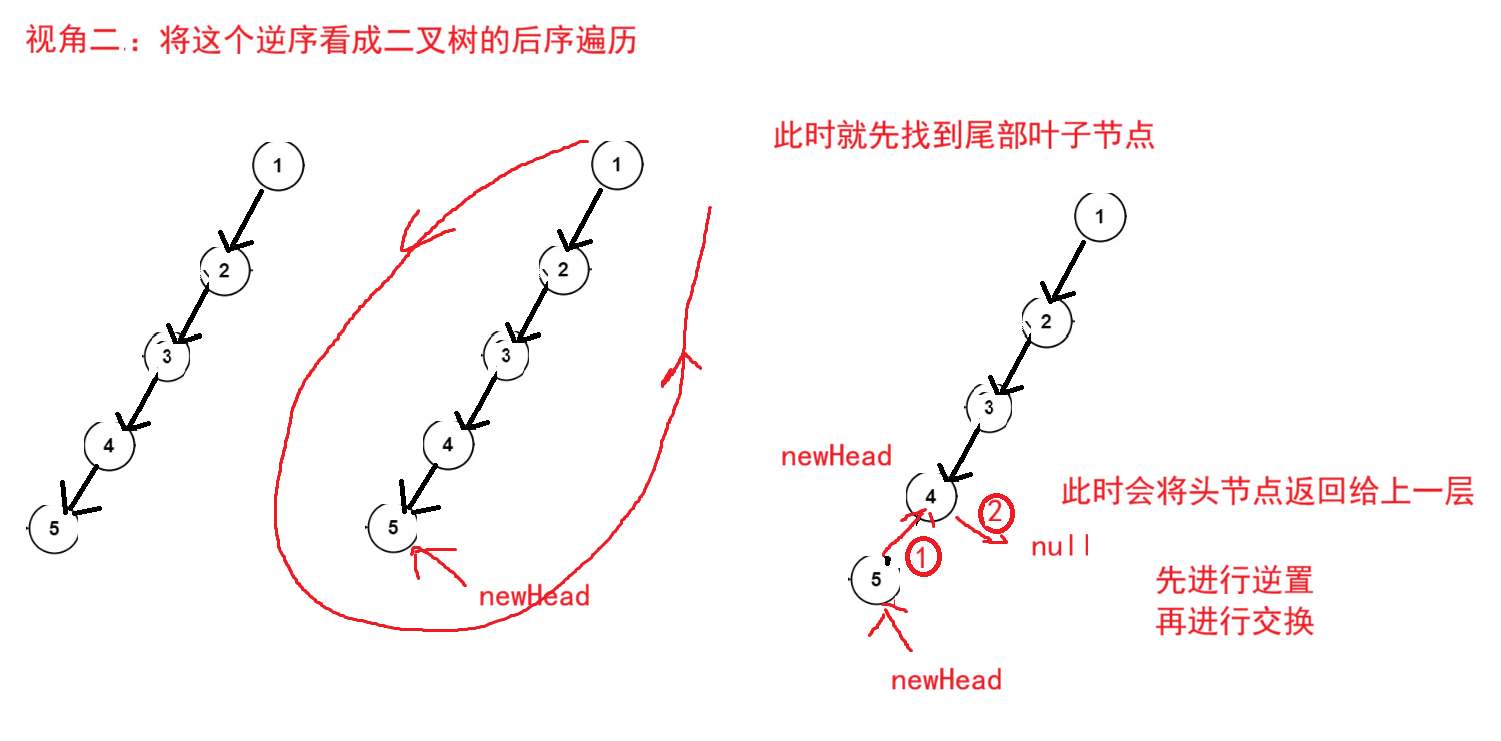
}反转链表
java
class Solution {
public ListNode reverseList(ListNode head) {
if(head == null || head.next == null){
return head;
}
ListNode newHead = reverseList(head.next);
head.next.next = head;
head.next = null;
return newHead;
}
}两两交换链表中的节点
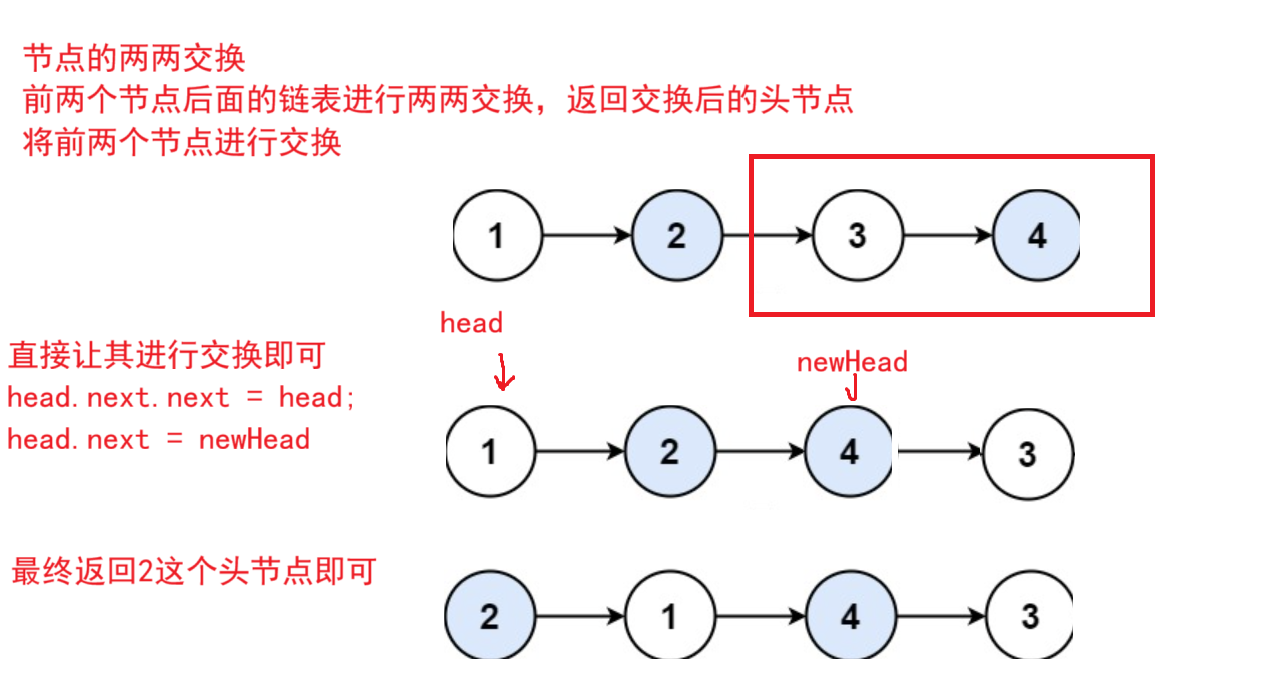
java
class Solution {
public ListNode swapPairs(ListNode head) {
if(head == null || head.next == null){
return head;
}
ListNode newHead = swapPairs(head.next.next);
ListNode tem = head.next;
head.next.next = head;
head.next = newHead;
return tem;
}
}Pow(x,n)
题目解析:就是求出x^n,求出x的n次幂,此时如果直接遍历可能会超时,因此这里采用快速幂的思想


java
class Solution {
public double myPow(double x, int n) {
return n < 0 ? 1/pow(x,-n) : pow(x,n);
}
public double pow(double x,long n ){
if(n == 0){
return 1;
}
double tem = pow(x,n/2);
return n % 2 == 0 ? tem * tem : tem * tem * x;
}
}二叉树相关题目
计算布尔二叉树的值
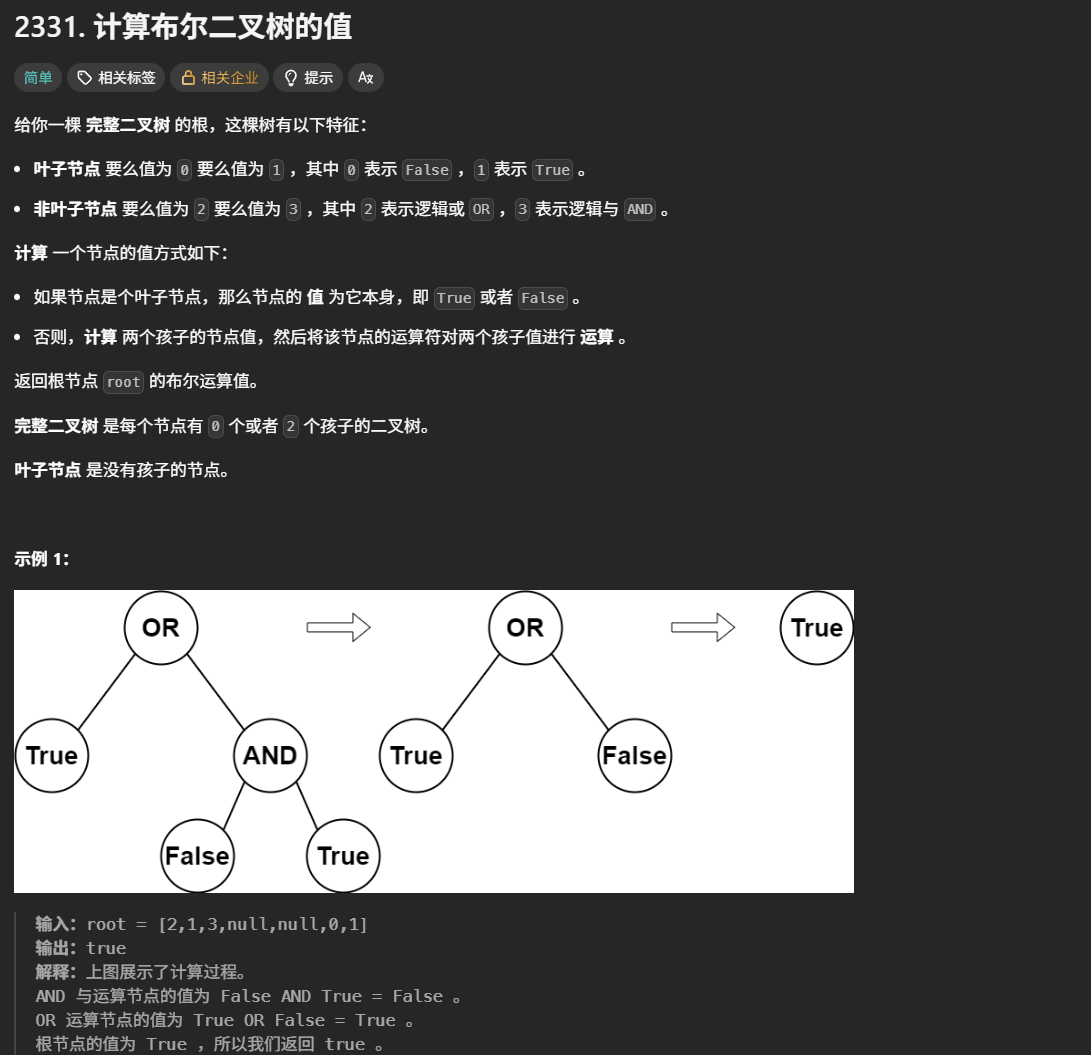
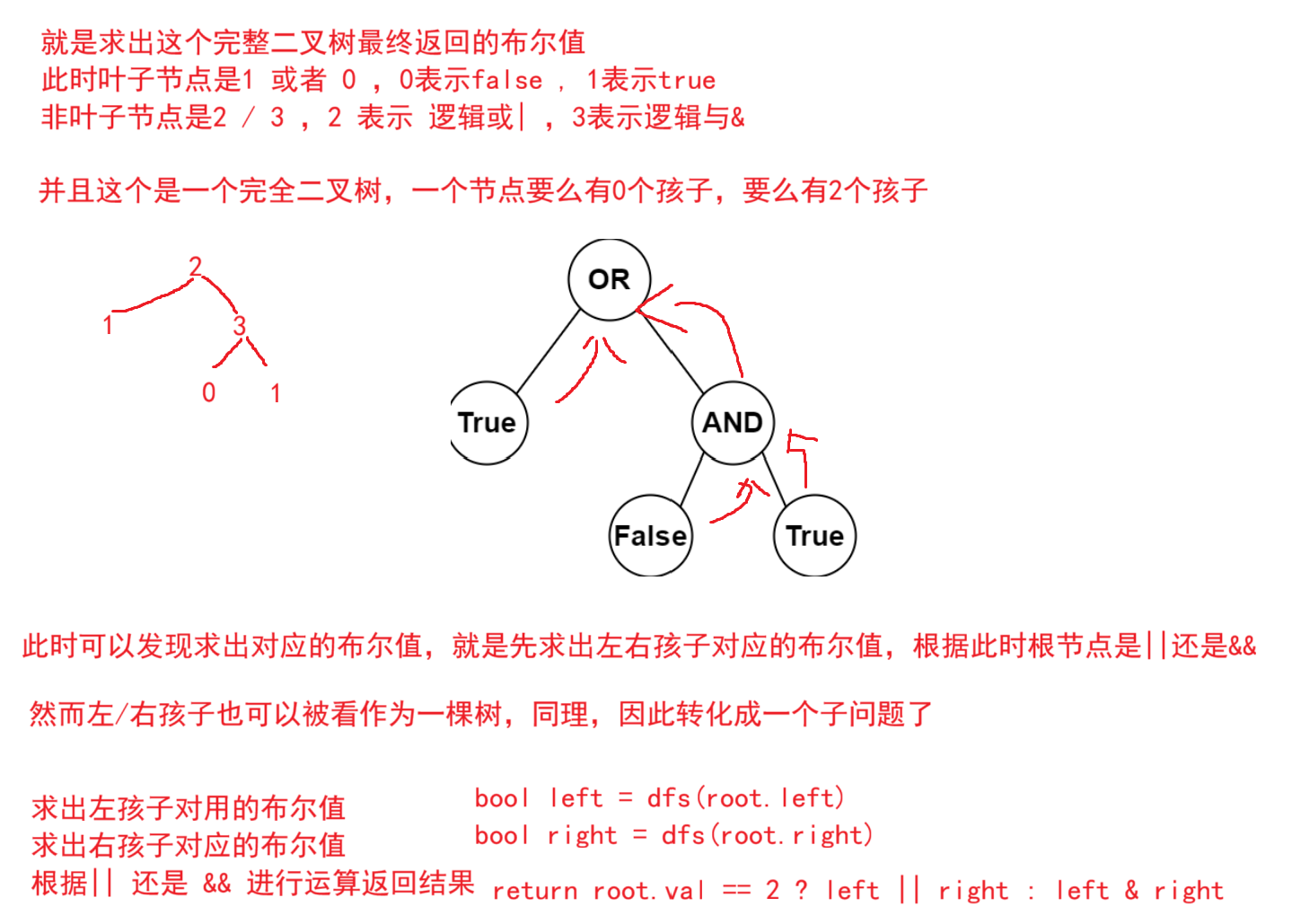
题目解析:求出这个完全二叉树对应的布尔值
java
class Solution {
public boolean evaluateTree(TreeNode root) {
if(root.left == null){
return root.val == 0 ? false : true;
}
boolean left = evaluateTree(root.left);
boolean right = evaluateTree(root.right);
return root.val == 2 ? left || right : left && right;
}
}求根节点到叶子节点数字之和
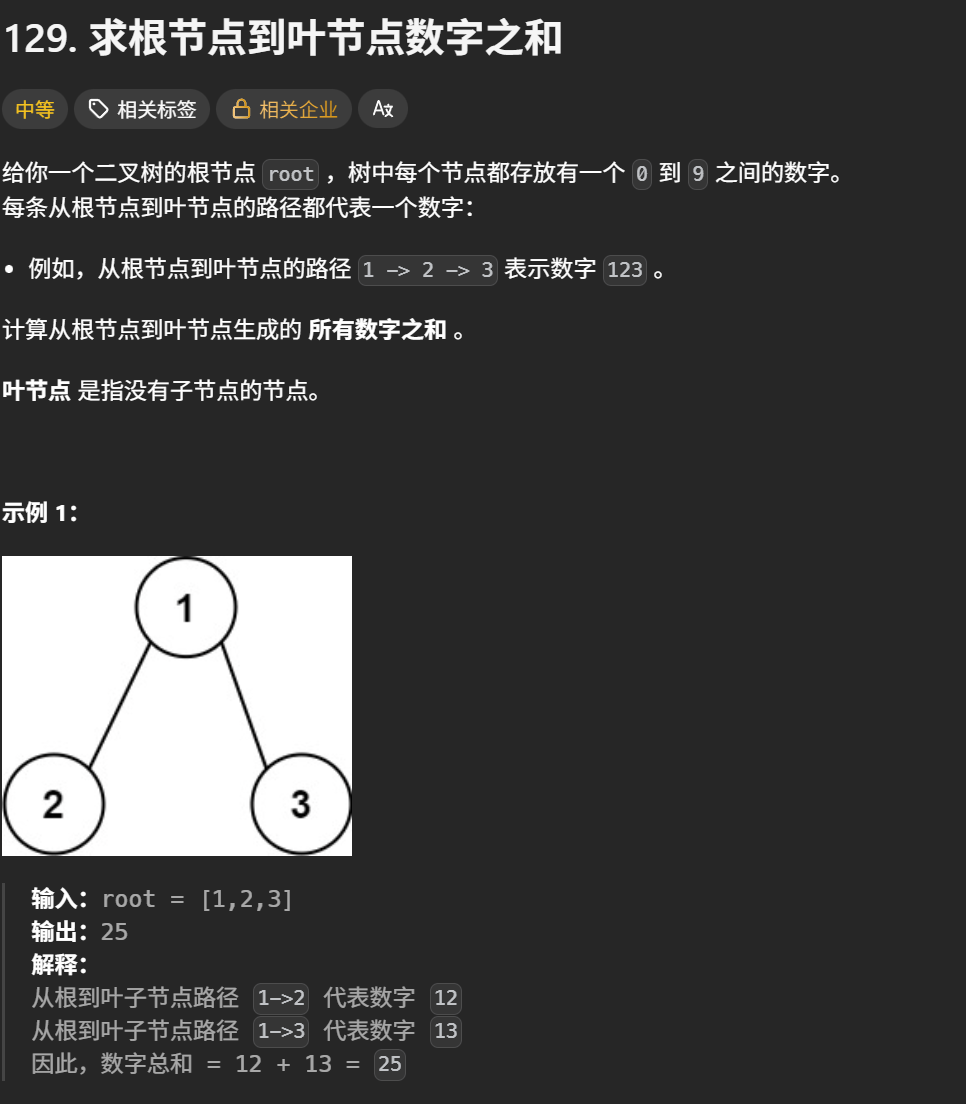
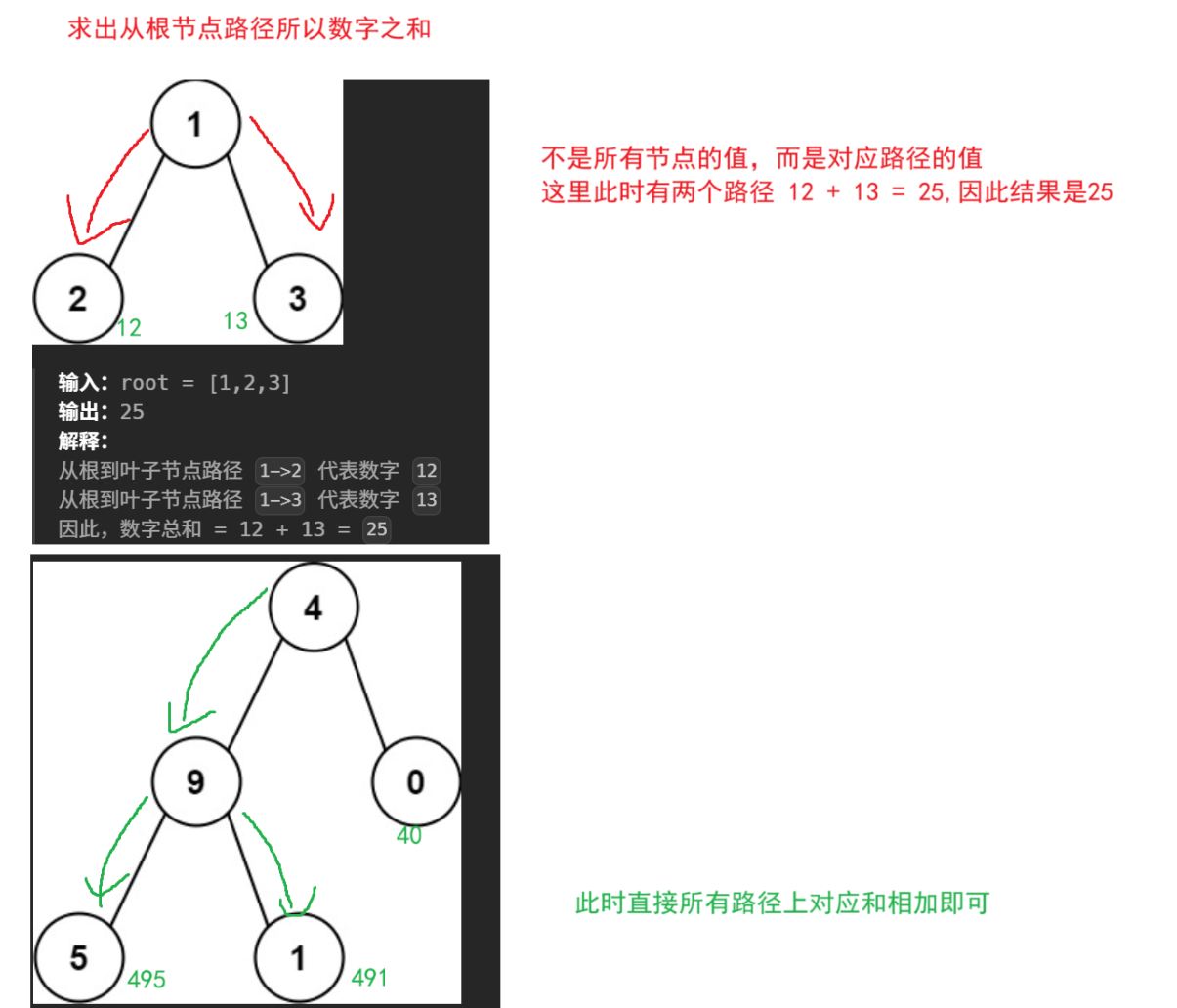
题目解析 :就是求出此时所有路径之和
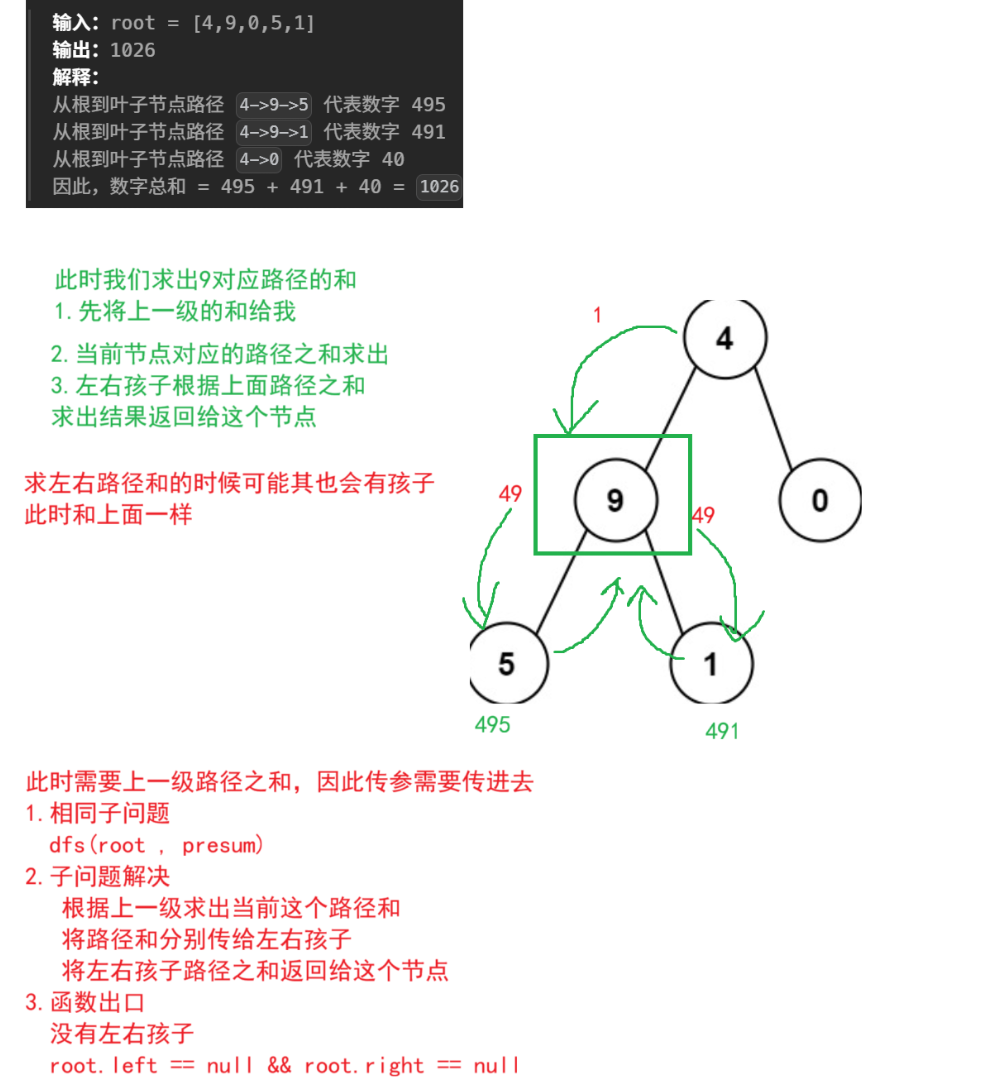
递归:这里求所有路径之和,求出左孩子对应路径 + 右孩子对应路径,此时左右孩子也可能作为根节点重复操作
java
class Solution {
public int sumNumbers(TreeNode root) {
return dfs(root, 0);
}
public int dfs(TreeNode root, int presum) {
//此时节点路径之和
presum = presum * 10 + root.val;
//叶子节点就结束
if (root.left == null && root.right == null) {
return presum;
}
int ret = 0;
//左孩子不为空,递归左边
if (root.left != null) {
ret += dfs(root.left, presum);
}
//右孩子不为空,递归右边
if (root.right != null) {
ret += dfs(root.right, presum);
}
return ret;
}
}二叉树剪枝

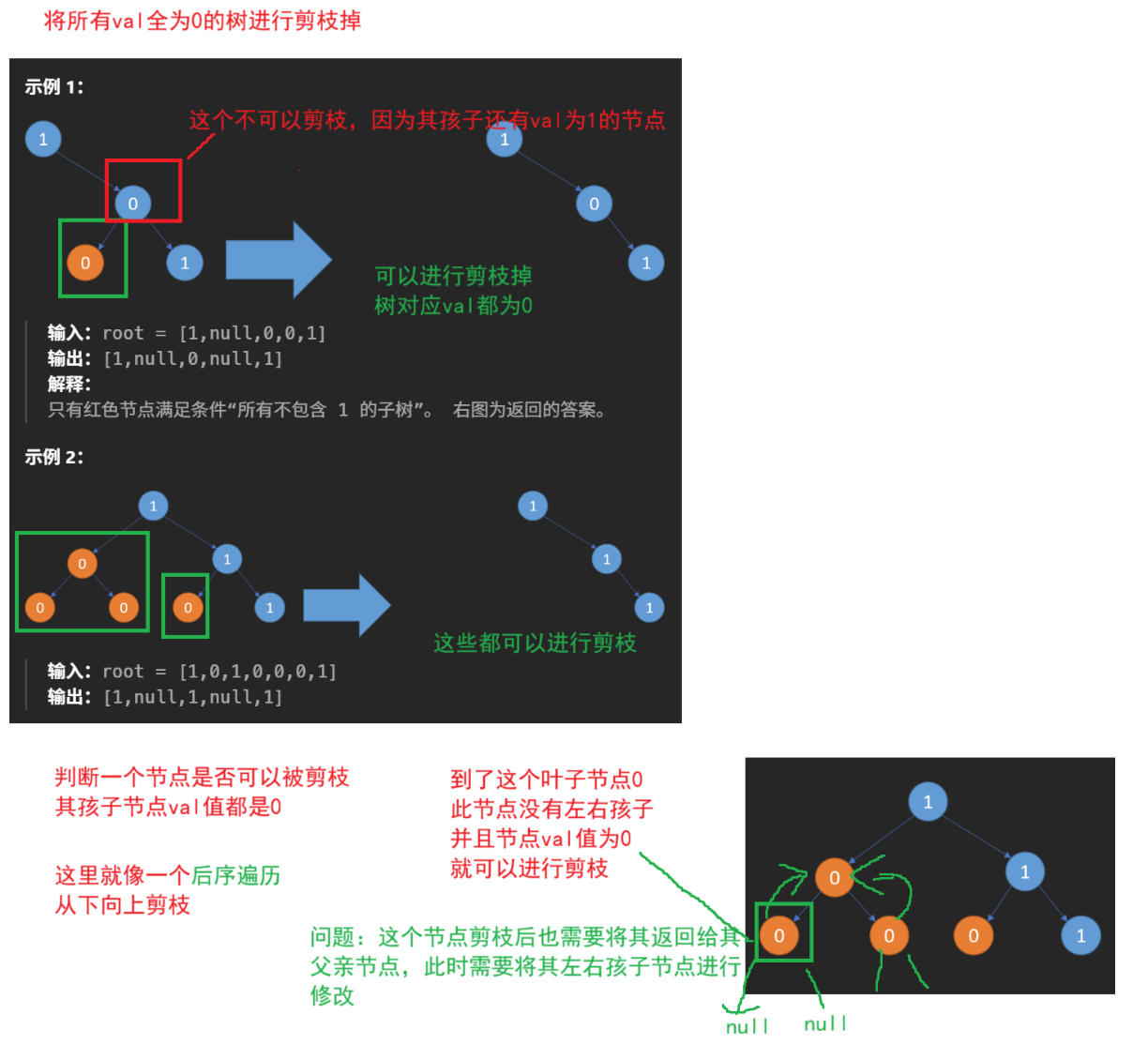
题目解析:就是将树中子树中的val全为0的节点进行剪枝

java
class Solution {
public TreeNode pruneTree(TreeNode root) {
if(root == null){
return null;
}
//左右子树
root.left = pruneTree(root.left);
root.right = pruneTree(root.right);
//叶子节点并且值为0
if(root.left == null && root.right == null && root.val == 0){
root = null;//将这个节点置为空也行,上面判断也会进行返回
//return null;//直接返回空
}
return root;
}
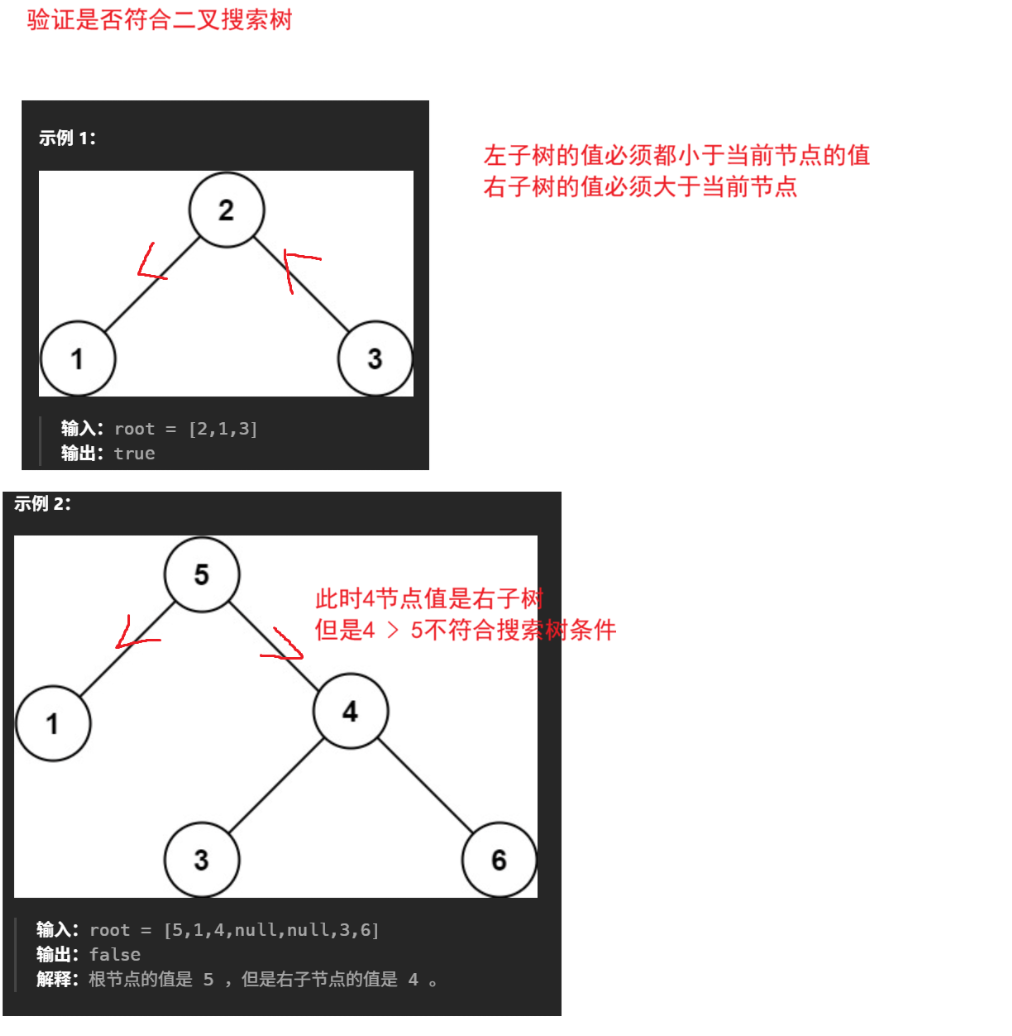
}验证二叉搜索树

题目解析 :一个树的左子树的值 < 当前节点值 < 右子树的值,那么这棵树满足二叉搜索树的条件
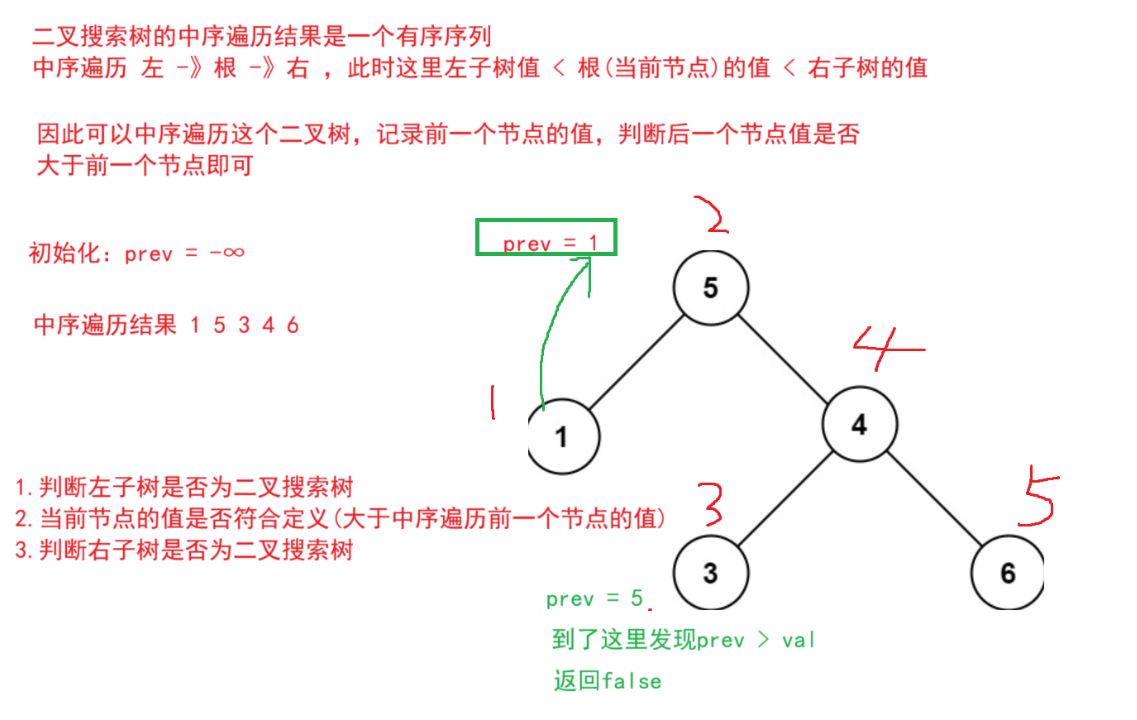
由于中序遍历也是这样的,因此可以转化为二叉树中序遍历是否有序
java
class Solution {
long prev = Long.MIN_VALUE;//记录上一个节点值
public boolean isValidBST(TreeNode root) {
//这里中序遍历这个树,如果是有效二叉搜索树中序遍历是有序的
if (root == null) {
return true;
}
boolean left = isValidBST(root.left);
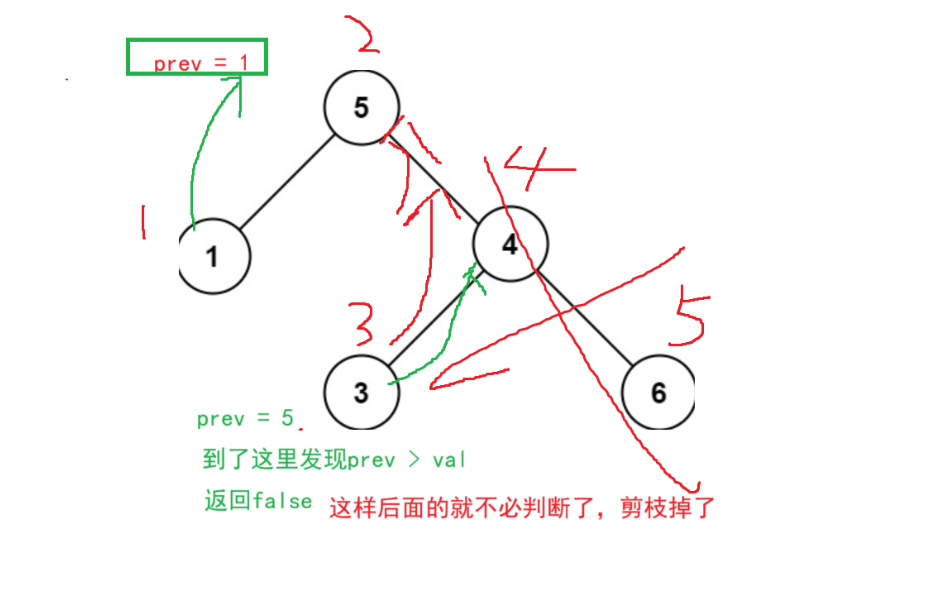
//剪枝,如果已经为空,此时不必遍历直接返回即可
if (left == false) {
return false;
}
if(root.val <= prev){
return false;
}
prev = root.val;
boolean right = isValidBST(root.right);
return left && right;
}
}二叉搜索树中第K小的元素
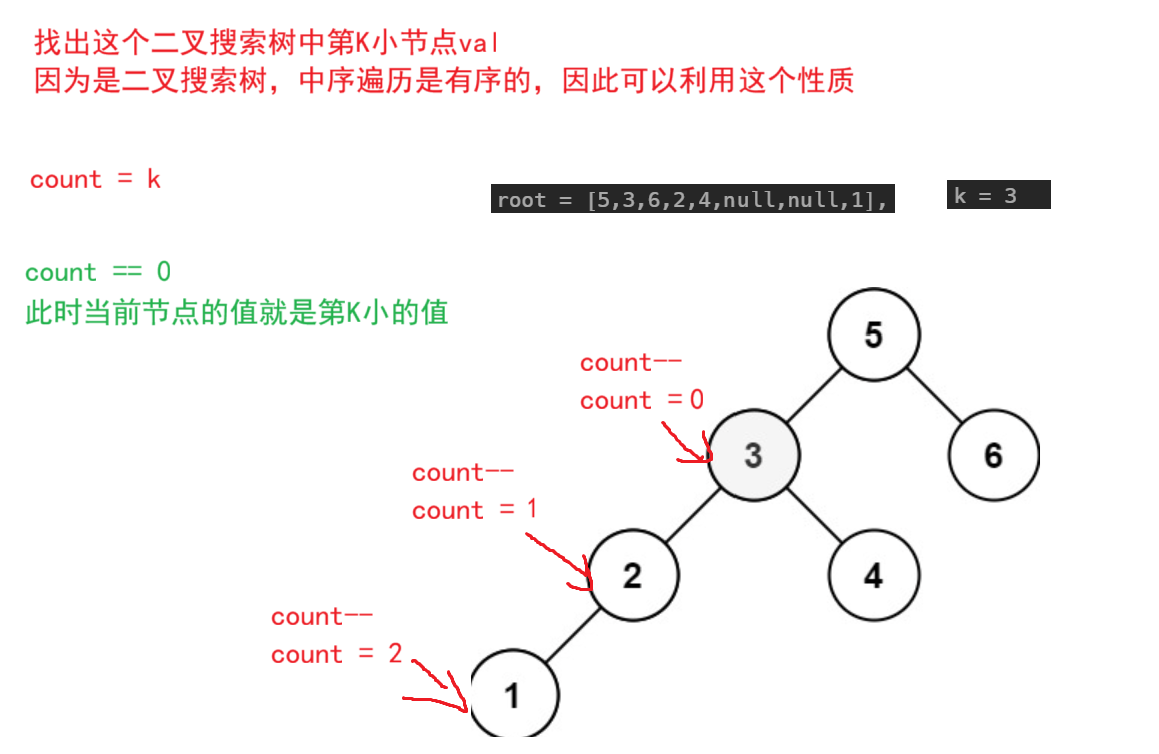
题目解析 :就是在一个二叉搜索树中找出其第K小元素
思路:和上一题一样,只不过这里需要一个count遍历来找出其第K小元素,每遍历一个节点count--,直到count == 0,此时这个节点就是要找的元素
java
class Solution {
int count = 0;
int ret = 0;
public int kthSmallest(TreeNode root, int k) {
count = k;
dfs(root);
return ret;
}
public void dfs(TreeNode root){
if(root == null || count == 0){
return;
}
dfs(root.left);//左子树
count--;
if(count == 0){
ret = root.val;
return;
}
dfs(root.right);//右子树
}
}二叉树的所有路径
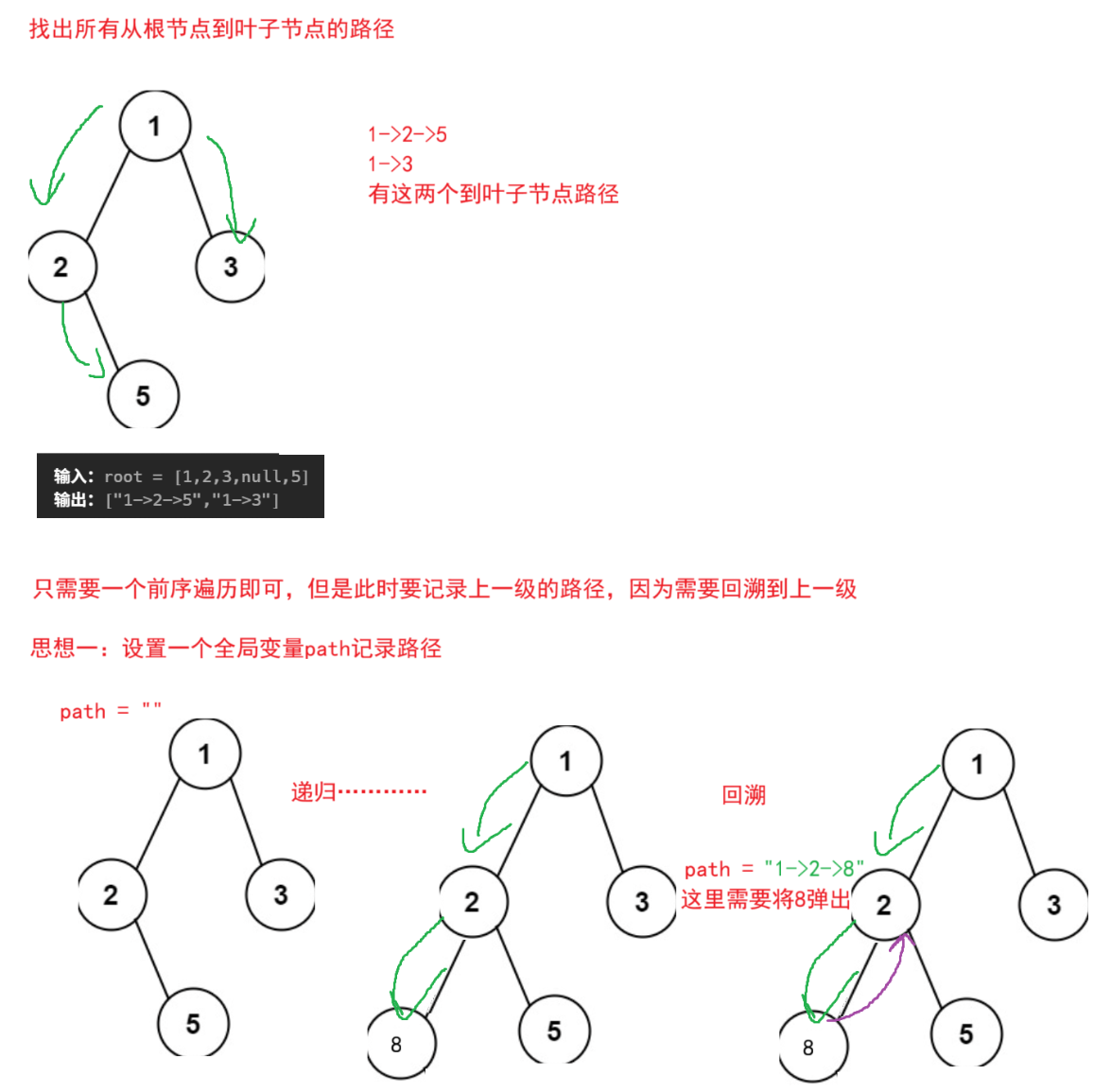
题目解析 :找出二叉树的所有路径
思想:递归进行拼接字符,到叶子节点就将其拼接到结果上,但是此时要注意保存上一级的路径
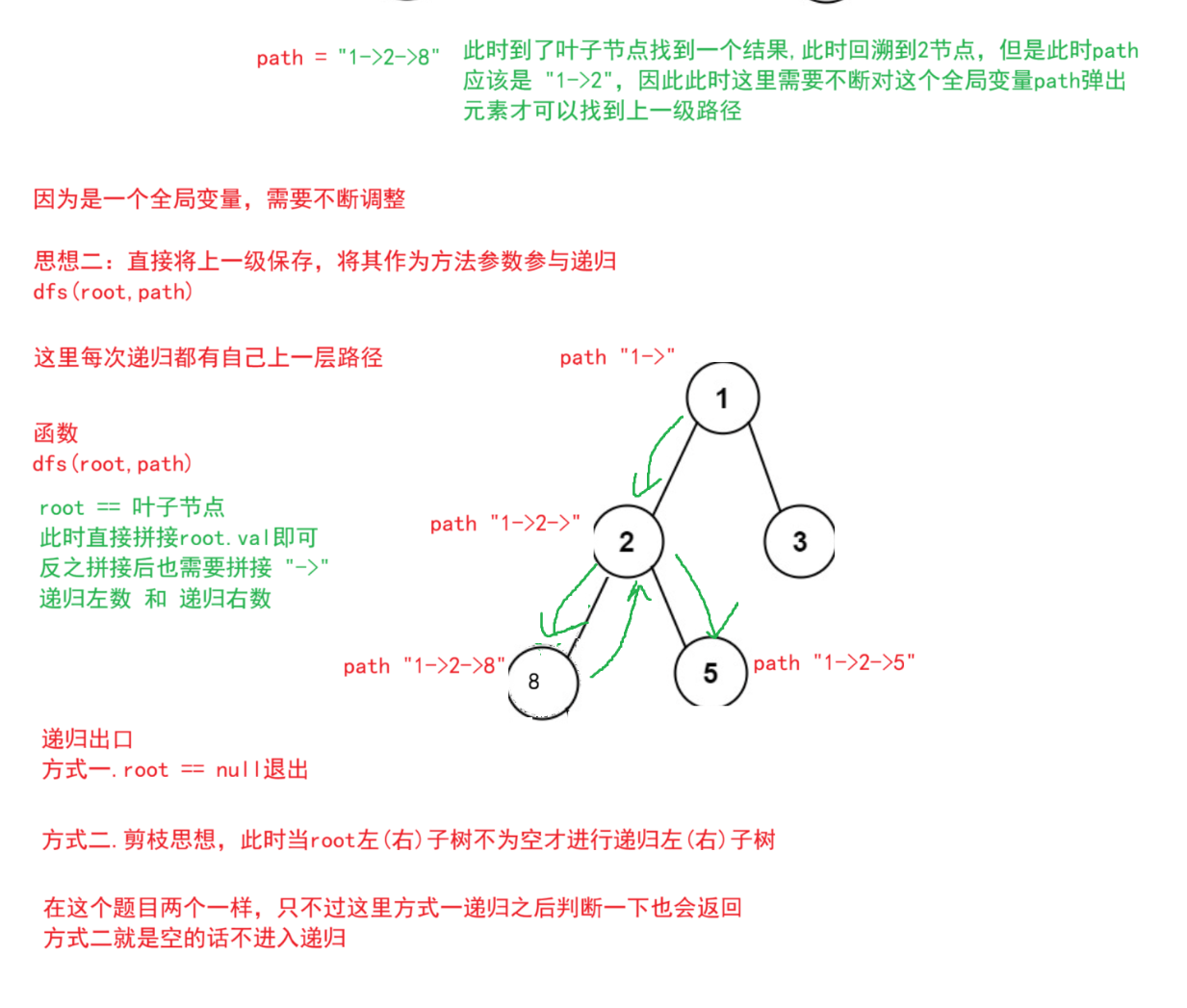
java
class Solution {
List<String> ret;
public List<String> binaryTreePaths(TreeNode root) {
ret = new ArrayList<>();
dfs(root,new StringBuffer());
return ret;
}
public void dfs(TreeNode root , StringBuffer path){
StringBuffer tem = new StringBuffer(path);//保存上一级路径用于回溯
tem.append(root.val + "");
//叶子节点
if(root.left == null && root.right == null){
ret.add(tem.toString());
return;
}else{
tem.append("->");
//小剪枝
if(root.left != null){
dfs(root.left,tem);
}
if(root.right != null){
dfs(root.right,tem);
}
}
}
}