基于ODE45的Lorenz动力系统仿真实现（MATLAB）

一、Lorenz系统原理与数学模型

Lorenz系统是描述大气对流运动的非线性动力系统，其微分方程为：

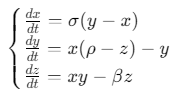
其中：

σσσ（普朗特数）：控制对流强度，典型值σ=10σ=10σ=10
ρρρ（瑞利数）：控制系统混沌行为，临界值ρ=24.74ρ=24.74ρ=24.74，典型值ρ=28ρ=28ρ=28
βββ（几何比）：控制垂直方向收缩，典型值β=8/3β=8/3β=8/3

当ρ>24.74ρ>24.74ρ>24.74时，系统呈现混沌行为，形成著名的Lorenz吸引子，表现为对初始条件的极端敏感（蝴蝶效应）。

二、MATLAB仿真实现步骤

1. 定义Lorenz方程函数

创建lorenz.m文件，描述微分方程：

matlab 复制代码

function dydt = lorenz(t, state, sigma, rho, beta)
    x = state(1); y = state(2); z = state(3);
    dxdt = sigma * (y - x);
    dydt = x * (rho - z) - y;
    dzdt = x * y - beta * z;
    dydt = [dxdt; dydt; dzdt];
end

2. 设置仿真参数与初始条件

matlab 复制代码

% 参数设置
sigma = 10;   % 普朗特数
rho = 28;     % 瑞利数（混沌临界值）
beta = 8/3;   % 几何比

% 初始条件（可调整）
initial_state = [1; 1; 1];  % 初始点 (x0, y0, z0)

% 时间范围与ODE45配置
tspan = [0, 50];          % 仿真时间 [0, 50]秒
options = odeset('RelTol', 1e-5, 'AbsTol', 1e-6);  % 精度控制

3. 调用ODE45求解方程

matlab 复制代码

[t, Y] = ode45(@(t, state) lorenz(t, state, sigma, rho, beta), tspan, initial_state);

4. 可视化结果

matlab 复制代码

% 三维轨迹图
figure;
plot3(Y(:,1), Y(:,2), Y(:,3), 'LineWidth', 0.5);
xlabel('X'); ylabel('Y'); zlabel('Z');
title('Lorenz Attractor (σ=10, ρ=28, β=8/3)');
grid on; view(3);

% 投影到不同平面
figure;
subplot(2,2,1); plot(Y(:,1), Y(:,3)); title('X-Z Projection');
subplot(2,2,2); plot(Y(:,2), Y(:,3)); title('Y-Z Projection');
subplot(2,2,3); plot(Y(:,1), Y(:,2)); title('X-Y Projection');
subplot(2,2,4); plot3(Y(:,1), Y(:,2), Y(:,3)); title('3D View');

三、关键结果分析

1. 混沌吸引子特征

三维轨迹：呈现"蝴蝶形"非周期运动
敏感依赖性：初始条件微小变化（如y0从1变为1.01）导致轨迹发

2. 参数敏感性分析

参数	临界值	行为变化
ρρρ	24.74	从周期运动进入混沌状态
σσσ	10	低于10时系统趋于稳定平衡点
βββ	8/3	改变收缩速率，影响吸引子形状

四、扩展实验设计

1. 初始条件敏感性验证

matlab 复制代码

% 不同初始条件对比
initial1 = [1; 1; 1];
initial2 = [1; 1.01; 1];
[t1, Y1] = ode45(@(t,state) lorenz(t,state,sigma,rho,beta), tspan, initial1);
[t2, Y2] = ode45(@(t,state) lorenz(t,state,sigma,rho,beta), tspan, initial2);

% 绘制X-Z平面对比
figure;
plot(Y1(:,1), Y1(:,3), 'r', Y2(:,1), Y2(:,3), 'b');
legend('Initial (1,1,1)', 'Initial (1,1.01,1)');
title('混沌敏感性：初始条件差异0.01');

2. 参数动态调整仿真

matlab 复制代码

% 实时调整ρ值观察分岔现象
rho_values = [10, 15, 20, 25, 30];
figure;
hold on;
for i = 1:length(rho_values)
    [~, Y] = ode45(@(t,state) lorenz(t,state,sigma,rho_values(i),beta), [0,50], initial_state);
    plot3(Y(:,1), Y(:,2), Y(:,3), 'DisplayName', ['ρ=',num2str(rho_values(i))]);
end
hold off;
legend;
title('参数ρ对Lorenz系统的影响');

参考代码用ODE45算法仿真Lorenz动力系统 www.youwenfan.com/contentcsr/99685.html

五、优化与注意事项

计算效率：

使用ode45的Jacobian选项提供雅可比矩阵，加速求解：

matlab 复制代码

function J = lorenz_jacobian(t, state, sigma, rho, beta)
    x = state(1); y = state(2); z = state(3);
    J = [ -sigma, sigma, 0;
          rho-z, -1, -x;
          y, x, -beta ];
end
options = odeset('Jacobian', @lorenz_jacobian);

硬件加速：
- 启用并行计算（需Parallel Computing Toolbox）：
  matlab 复制代码
```
options = odeset('UseParallel', true);
```

可视化增强：

添加动画展示轨迹演化：

matlab 复制代码

figure; plot3(Y(:,1), Y(:,2), Y(:,3), 'LineWidth', 0.5);
for i = 1:size(Y,1)
    plot3(Y(1:i,1), Y(1:i,2), Y(1:i,3), 'LineWidth', 0.5);
    drawnow; pause(0.01);
end

六、结论

通过ODE45算法成功仿真了Lorenz系统的混沌行为，验证了其对参数和初始条件的敏感性。此方法可扩展应用于其他非线性动力系统（如Rossler系统、Chua电路）的研究。