RoPE相对位置编码

首先说一下绝对位置编码的缺点.

绝对位置编码通常是在输入的时候编入input:

x = x + pe

这里的pe会改变x的方向和大小, 造成x的语义被搞脏了. 因此引入旋转位置编码.

一个二维向量x逆时针旋转 α \alpha α度, 新的向量表示为, x为行向量:
x ′ = x @ [ c o s α − s i n α s i n α c o s α ] x' = x @ \begin{bmatrix} cos\alpha & -sin\alpha \\\\ sin\alpha & cos\alpha \\\\ \end{bmatrix} x′=x@ cosαsinα−sinαcosα

这样向量长度不变, 方向逆时针旋转 α \alpha α.

因此在LLM中, 我们标记token的index为 0 , 1 , 2 , ⋯ n 0, 1, 2, \cdots n 0,1,2,⋯n. 对于第 i i i个token, 我们逆时针旋转 i θ i\theta iθ度, 对于第j个词, 我们逆时针旋转 j θ j\theta jθ度.

第 i i i个token(q)和第 j j j个token(k)旋转后的向量分别为:
q ′ = q @ [ c o s ( i θ ) − s i n ( i θ ) s i n ( i θ ) c o s ( i θ ) ] q' = q @ \begin{bmatrix} cos(i\theta) & -sin(i\theta) \\\\ sin(i\theta) & cos(i\theta) \\\\ \end{bmatrix} q′=q@ cos(iθ)sin(iθ)−sin(iθ)cos(iθ)

k ′ = k @ [ c o s ( j θ ) − s i n ( j θ ) s i n ( j θ ) c o s ( j θ ) ] k' = k@\begin{bmatrix} cos(j\theta) & -sin(j\theta) \\\\ sin(j\theta) & cos(j\theta) \\\\ \end{bmatrix} k′=k@ cos(jθ)sin(jθ)−sin(jθ)cos(jθ)

为了方便, 我们记前面的旋转矩阵为: R ( θ ) = [ c o s θ − s i n θ s i n θ c o s θ ] R(\theta)=\begin{bmatrix} cos\theta& -sin\theta\\\\ sin\theta& cos\theta\\\\ \end{bmatrix} R(θ)= cosθsinθ−sinθcosθ

第 i i i个token(q)和第 j j j个token(k)的attention计算为:
a t t e n t i o n = q ′ @ k ′ T = q @ R ( i θ ) @ [ k @ R ( j θ ) ] T = q @ R ( i θ ) @ R ( j θ ) T @ k T = q @ [ R ( i θ ) @ R ( j θ ) T ] @ k T = q @ R ( j θ − i θ ) @ k T attention = q' @ k'^T=q@R(i\theta) @[k@R(j\theta)]^T=\\ q@R(i\theta) @R(j\theta)^T@k^T=\\ q@[R(i\theta) @R(j\theta)^T]@k^T=\\ q@R(j\theta-i\theta)@k^T attention=q′@k′T=q@R(iθ)@[k@R(jθ)]T=q@R(iθ)@R(jθ)T@kT=q@[R(iθ)@R(jθ)T]@kT=q@R(jθ−iθ)@kT

这里 j θ − i θ j\theta-i\theta jθ−iθ刚好是token i和token j之间旋转角度的差值, 满足距离越近越大, 距离越远越小.

如果是多维的向量, 我们就两两分组, 分别旋转.

但是这里的问题是, 可能会覆盖. 比如旋转10度和370会重合. 因此这里引入了不同的旋转频率. 在i(i为特征的第i维)较小的时候旋转的快一些, 让模型能够捕获相对位置较小的2个token之间的差异. 但是此时对于i较大的维度, 响铃位置的相对位置感知不明显, 但是对于距离较远的2个token之间的变化感受明显.

为什么要使用指数呢?

如果使用乘法, 则会让高频部分的维度太多, 因为高频部分在相对位置较近的时候会疯狂旋转, 如果这样的维度太多了, 模型直接崩溃. 而且会导致低频部分的维度不够, 因为低频部分能够正常感知位置变化(不会疯狂旋转).

指数在log空间是均匀覆盖的. 类似于第1组->能够区分的距离尺度 1 ∼ 0 1\sim 0 1∼0; 第2组: 能够区分距离的尺度: 10 ∼ 100 10\sim 100 10∼100. 第三组: 100 ∼ 1000 100\sim 1000 100∼1000. 这样能够覆盖尽可能多的距离. 否则第一组 1 ∼ 10 1\sim 10 1∼10, 第2组 10 ∼ 20 10\sim 20 10∼20, 这样就不利于区分.

对于q, k的前2维, 当距离较远的2个token计算attention score时, 他们的贡献是近似随机的. 因此高频部分只能捕捉距离较近的2个token之间的差异.

为什么RoPE具有远程衰减的特性

这里的远程衰减是统计学意义上的, 并不是严格的数学证明. 也就是说对于大多数随机的q, k, 相对距离较远的两个token之间的分数会比相对距离较远的两个token之间的分数大. 因此呈现震荡衰减的特性:

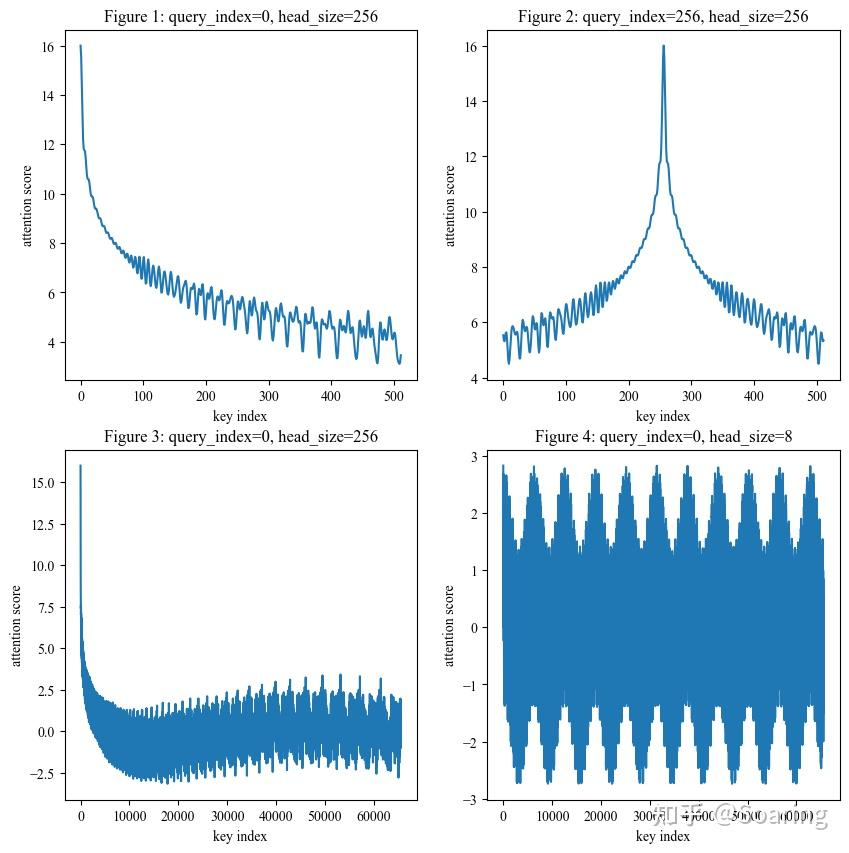
如何外推(extrapolation)

训练的时候样本一般序列长度较短, 比如2048, 但是推理的上下文长度可能达到几万几十万

• Positional Interpolation
• NTK-aware Scaled RoPE

旋转式位置编码 (RoPE) 知识总结

transformers库各种rope外推变体

典型extrapolation

NTK dynamic scaling

testing的时候动态记录新的seq_len, 如果新的seq_len>train_max_len: 则会采用如下方式对频率进行缩放. 核心代码:

"""
如果当前序列长度超过之前缓存的最大值。
说明：
1. 之前没见过这么长
2. 需要重新计算频率
"""
if seq_len > max_seq_len_cached:  # growth
		# 根据 rope_type 选择对应用什么函数来跟新频率。
    rope_init_fn = ROPE_INIT_FUNCTIONS[rope_type]

		# 真正更新频率的部分
    inv_freq, self.attention_scaling = rope_init_fn(
        self.config,
        device,
        seq_len=seq_len,
        layer_type=layer_type,
    )
    # TODO joao: may break with compilation
    """
		把新的 inv_freq 注册为 buffer。
		persistent=False → 不会保存进模型权重
		只是运行时状态
		"""
    self.register_buffer(f"{prefix}inv_freq", inv_freq, persistent=False)
		
		# 更新缓存的最大长度。避免重复计算。
    setattr(self, f"{layer_type}_max_seq_len_cached", seq_len)

"""
reset: 当前序列已经回到训练长度以内, 但之前跑过超长.
1. 如果新的seq_len超过了之前的最大值, 就更新频率. 
2. 如果新的seq_len小于之前最大的, 用之前最大的
3. 如果新的seq_len小于train_max_seq_len, 用train_max_seq_len
"""
if seq_len < self.original_max_seq_len and max_seq_len_cached > self.original_max_seq_len:  # reset
    original_inv_freq = original_inv_freq.to(device)
    self.register_buffer(f"{prefix}inv_freq", original_inv_freq, persistent=False)
    setattr(self, f"{prefix}original_inv_freq", original_inv_freq)
    setattr(self, f"{layer_type}_max_seq_len_cached", self.original_max_seq_len)

qwen3默认的rope_init_func, 也就是如果发现seq_len太大, 直接重新计算频率(default):

class Qwen3VLTextRotaryEmbedding(nn.Module):
    inv_freq: torch.Tensor  # fix linting for `register_buffer`

    def __init__(self, config: Qwen3VLTextConfig, device=None):
        super().__init__()
        self.max_seq_len_cached = config.max_position_embeddings
        self.original_max_seq_len = config.max_position_embeddings

        self.config = config

        self.rope_type = self.config.rope_parameters["rope_type"]
        rope_init_fn: Callable = self.compute_default_rope_parameters
        if self.rope_type != "default":
            rope_init_fn = ROPE_INIT_FUNCTIONS[self.rope_type]
        inv_freq, self.attention_scaling = rope_init_fn(self.config, device)

        self.register_buffer("inv_freq", inv_freq, persistent=False)
        self.register_buffer("original_inv_freq", inv_freq.clone(), persistent=False)

        self.mrope_section = config.rope_parameters.get("mrope_section", [24, 20, 20])
@staticmethod
    def compute_default_rope_parameters(
        config: Qwen3VLTextConfig | None = None,
        device: Optional["torch.device"] = None,
        seq_len: int | None = None,
    ) -> tuple["torch.Tensor", float]:
        base = config.rope_parameters["rope_theta"]
        dim = getattr(config, "head_dim", None) or config.hidden_size // config.num_attention_heads

        attention_factor = 1.0  # Unused in this type of RoPE

        # Compute the inverse frequencies
        inv_freq = 1.0 / (
            base ** (torch.arange(0, dim, 2, dtype=torch.int64).to(device=device, dtype=torch.float) / dim)
        )
        return inv_freq, attention_factor

def dynamic_frequency_update(self, position_ids, device, layer_type=None):
    seq_len = torch.max(position_ids) + 1
    if layer_type is None:
        rope_type = self.rope_type
        max_seq_len_cached = self.max_seq_len_cached
        original_inv_freq = self.original_inv_freq
        prefix = ""
    else:
        rope_type = self.rope_type[layer_type]
        max_seq_len_cached = getattr(self, f"{layer_type}_max_seq_len_cached", self.max_seq_len_cached)
        original_inv_freq = getattr(self, f"{layer_type}_original_inv_freq")
        prefix = f"{layer_type}_"
		
    if seq_len > max_seq_len_cached:  # growth
        rope_init_fn = ROPE_INIT_FUNCTIONS[rope_type]
        inv_freq, self.attention_scaling = rope_init_fn(
            self.config,
            device,
            seq_len=seq_len,
            layer_type=layer_type,
        )
        # TODO joao: may break with compilation
        self.register_buffer(f"{prefix}inv_freq", inv_freq, persistent=False)
        setattr(self, f"{layer_type}_max_seq_len_cached", seq_len)

    if seq_len < self.original_max_seq_len and max_seq_len_cached > self.original_max_seq_len:  # reset
        # This .to() is needed if the model has been moved to a device after being initialized (because
        # the buffer is automatically moved, but not the original copy)
        # 取训练时候的freq
        original_inv_freq = original_inv_freq.to(device)
        self.register_buffer(f"{prefix}inv_freq", original_inv_freq, persistent=False)
        setattr(self, f"{prefix}original_inv_freq", original_inv_freq)
        setattr(self, f"{layer_type}_max_seq_len_cached", self.original_max_seq_len)

python代码实现

第i对的频率计算公式:
θ i = θ − 2 ∗ ( i − 1 ) d = 1 θ 2 ( i − 1 ) d \theta_i = \theta^{-\frac{2*(i-1)}{d}}=\frac{1}{\theta^\frac{{2(i-1)}}{d}} θi=θ−d2∗(i−1)=θd2(i−1)1

def pre_compute_freq(seq_len, dim, theta):
	freqs = 1/theta ** (2*torch.arange(0, dim, 2)/d)
	pos = torch.arange(0, seq_len)
	rot_theta = torch.outer(pos, freqs)

	cos, sin = rot_theta.cos(), rot_theta.sin()
	return cos, sin

注意这里的freqs是按照2个位置一个值, 因此shape为(d/2,), pos的shap为(seq_len, ). rot_theta的shape为(seq_len, d/2), 表示第 i i i个位置的token的第 j j j对特征的旋转角度.

接下来实现得到了旋转角度, 如何来计算q@R(n-m)@k^T

我们假设q向量为(x, y), 旋转角度 θ \theta θ之后q变为:
q ′ = ( x , y ) @ [ c o s θ − s i n θ s i n θ c o s θ ] = ( x c o s θ + y s i n θ , − x s i n θ + y c o s θ ) = ( x , y ) ∗ c o s θ + ( y , − x ) ∗ s i n θ q' = (x, y) @ \begin{bmatrix} cos\theta & -sin\theta\\ sin\theta & cos\theta \end{bmatrix}=(xcos\theta+ysin\theta, -xsin\theta+ycos\theta)= \\ (x, y) * cos\theta+(y, -x)*sin\theta q′=(x,y)@[cosθsinθ−sinθcosθ]=(xcosθ+ysinθ,−xsinθ+ycosθ)=(x,y)∗cosθ+(y,−x)∗sinθ

所以我们需要先求类似(y, -x)这样的向量. 对于多维, 转换方式为:

def rotate_half(x):
    """Rotates half the hidden dims of the input."""
    x1 = x[..., : x.shape[-1] // 2]
    x2 = x[..., x.shape[-1] // 2 :]
    return torch.cat((-x2, x1), dim=-1)

这里的方式有点奇怪, 不像是每一对来进行变换. 原因是为了实现方便. 因为一个token内的特征各个维度之间并不一定要遵循严格的顺序来分成若干对.

对于这里的实现, 我们的分组方式是(x0, x1, x2, x3), 把(x0, x2)分成一组, 把(x1, x3)分成一组. 按照这种分组方式, (x, y)变换完成之后(-x2, -x3, x0, x1), 即(x0, x2)这一组变成了(-x2, x0), (x1, x3)变成了(-x3, x1). 与公式要求的一样的.

因此:

(x, y) = q
(-y, x) = rotate_half(q)

执行 ( x , y ) ∗ c o s + ( − y , x ) ∗ s i n = q ∗ c o s + r o t a t e _ h a l f ( q ) ∗ s i n (x, y) * cos + (-y, x)*sin=q*cos+rotate\_half(q)*sin (x,y)∗cos+(−y,x)∗sin=q∗cos+rotate_half(q)∗sin:

def apply_rotary_pos_emb(q, k, cos, sin):
	q_embed = (q * cos) + (rotate_half(q) * sin)
  	k_embed = (k * cos) + (rotate_half(k) * sin)
  	return q_embed, k_embed

因此完整的实现涉及到3个函数, 其中pre_compute_freq是与计算 c o s m θ cosm\theta cosmθ和 s i n m θ sin m\theta sinmθ; rotate_half是对一对子空间(x, y)变换成(-y, x)方便后面计算; apply_rotary_pos_emb是计算 ( x , y ) ∗ c o s θ + ( y , − x ) ∗ s i n θ (x, y) * cos\theta+(y, -x)*sin\theta (x,y)∗cosθ+(y,−x)∗sinθ, 即执行旋转操作.

def pre_compute_freq(seq_len, dim, theta):
	freqs = 1/theta ** (2*torch.arange(0, dim, 2)/d)
	pos = torch.arange(0, seq_len)
	rot_theta = torch.outer(pos, freqs)

	cos, sin = rot_theta.cos(), rot_theta.sin()
	return cos, sin

def rotate_half(x):
    """Rotates half the hidden dims of the input."""
    x1 = x[..., : x.shape[-1] // 2]
    x2 = x[..., x.shape[-1] // 2 :]
    return torch.cat((-x2, x1), dim=-1)

def apply_rotary_pos_emb(q, k, cos, sin):
	q_embed = (q * cos) + (rotate_half(q) * sin)
  	k_embed = (k * cos) + (rotate_half(k) * sin)
  	return q_embed, k_embed

vision下的2维rope

一半用前dim//2来进行row的旋转, 后边dim//2来进行column的旋转, 然后把两部分合起来.