最长回文子串解析

前言

算法部分是我们参加工作面试的重中之重'

最长回文子串是一道面试算法常考题，也是我们算法练习中必不可少的一道题目

我们今天以多种角度去处理这道题目

1.中心拓展算法

分析逻辑

根据我们图中所画出的，中心拓展算法呢就是遍历i，以i为中心，去向两边扩散，找出最长子串

但需注意回文子串的长度存在奇数与偶数区别，如下图所示

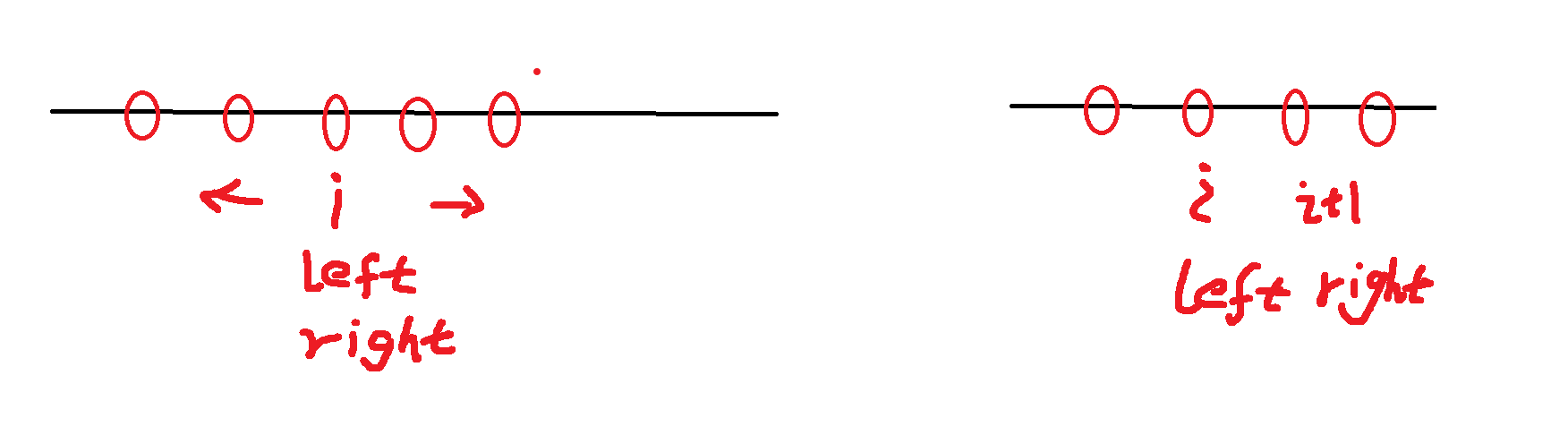
他们两个的遍历起始位置有所差别，我们要想找到最长子串，我们就需要考虑这两种逻辑

以此进行展开遍历这就是我们使用中心拓展算法解决这道问题的逻辑

这种解法的算法时间复杂度很明显是O(n²) 空间复杂度是O(1)；

补充一下substring的用法

两种重载方式：

1.substring(int beginIndex)：beginIndex 是起始索引（从 0 开始），表示从字符串的这个位置开始截取，一直到字符串的末尾。

2.substring(int beginIndex, int endIndex)：不包含结束索引 位置的字符，截取的子串长度 = endIndex - beginIndex

源码如下：

java 复制代码

 public String longestPalindrome(String s) {
     //中心拓展算法
        int begin=0,len=0;
        int left=0,right=0;
        for(int i=0;i<s.length();i++){
            //奇数遍历
            right=left=i;
            while(left>=0&&right<s.length()&&s.charAt(left)==s.charAt(right)){
                left--;
                right++;
            }
             if(right-left-1>len){
                len=right-left-1;
                begin=left+1;
            }
             //偶数遍历
            left=i;
            right=left+1;
            while(left>=0&&right<s.length()&&s.charAt(left)==s.charAt(right)){
                left--;
                right++;
            }
            if(right-left-1>len){
                len=right-left-1;
                begin=left+1;
            }
        }
       
        return s.substring(begin,begin+len);
    }

2.动态规划的解法

看逻辑图我们可以看到 dp表以i为起始 j为结束

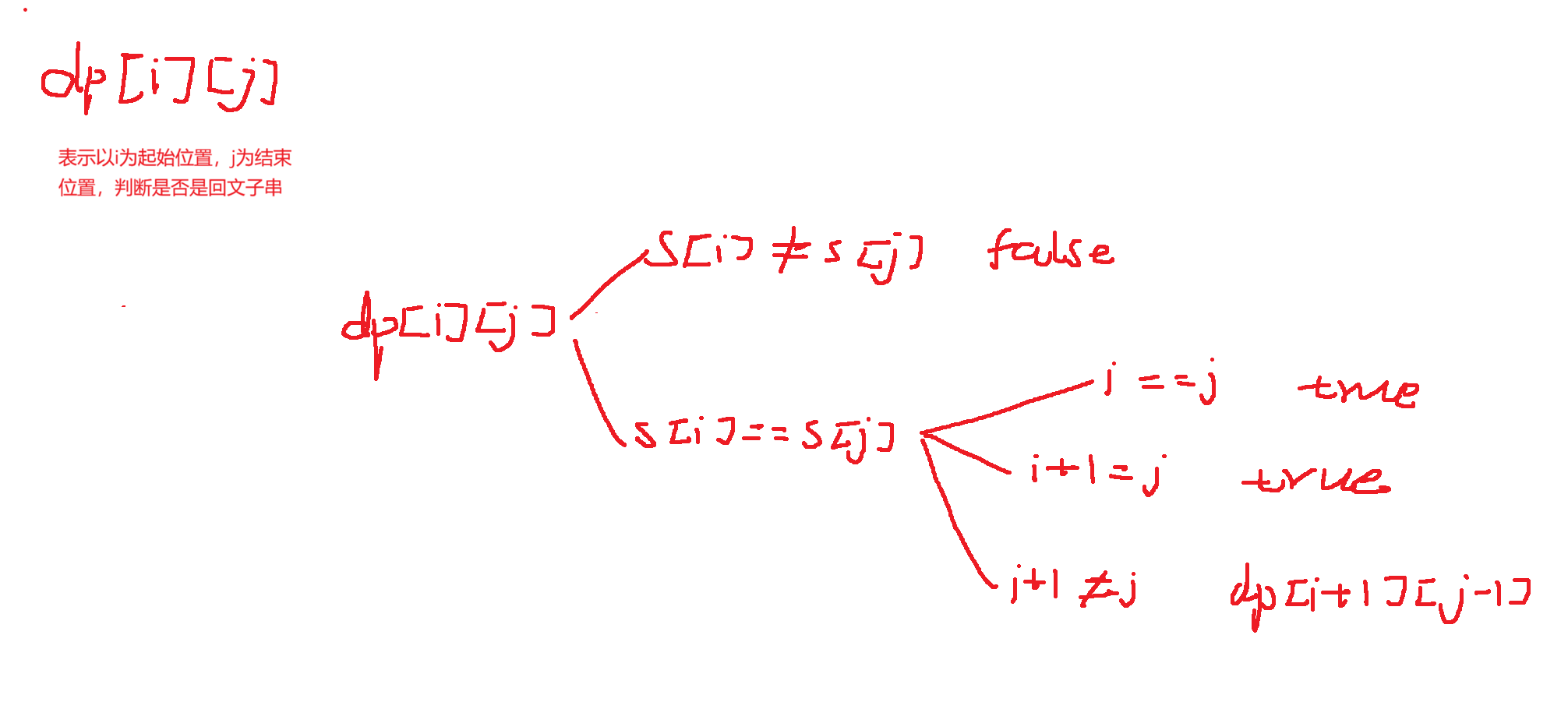
当s $i$ !=s $j$ ，此时dp $i$ $j$ 肯定不是回文子串此时就为false

当s $i$ ==s $j$ ，此时会有三种情况 i与j位置一样那它只是一个字符肯定是回文子串，

或者i+1==j，说明i和j相邻，此时也是回文子串

当i+1！=j，此时需要看内部字符串是不是满足回文就是dp $i+1$ $j-1$ 的结果

按照这个逻辑我们得出填表顺序，从下往上填表而且遍历时保证j不能大于i

该算法时间复杂度为O(n²) 空间复杂度也为O(n²)

java 复制代码

public String longestPalindrome(String s) {
        int n=s.length();
        //初始dp表
        boolean dp[][]=new boolean[n][n];
        //初始化
        //填表
        int begin=0,len=0;
        for(int i=n-1;i>=0;i--){
            for(int j=i;j<n;j++){
              if(s.charAt(i)==s.charAt(j)){
               dp[i][j]= i+1<j?dp[i+1][j-1]:true;
              }
              if(dp[i][j]&&j-i+1>len){
                len=j-i+1;
                begin=i;
              }

            }
        }
        return s.substring(begin,begin+len);
        
    }

这两种方法是解决该问题的主流方法