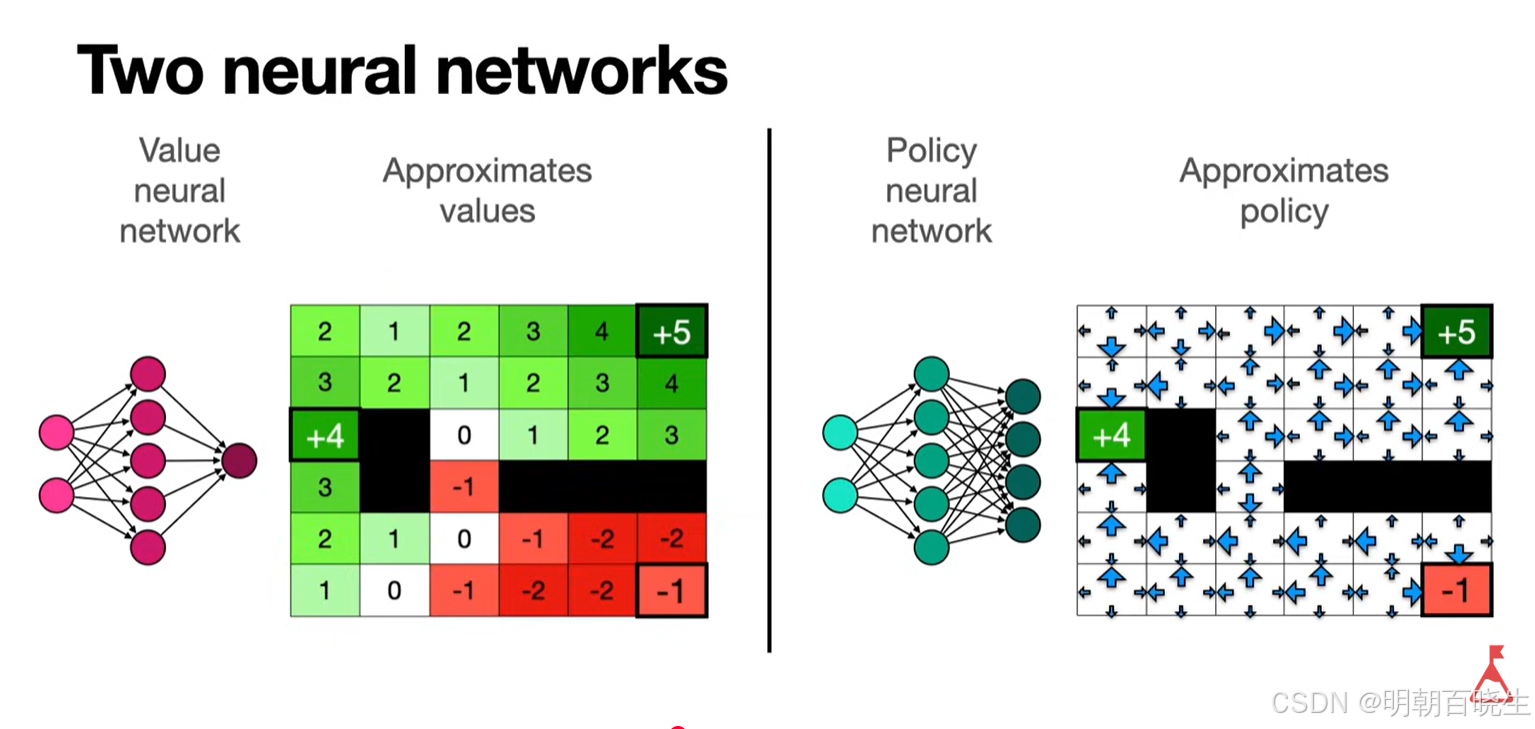
摘要：
前面策略一直以表格形式呈现：所有状态的动作概率均存储于表中。
本章将展示策略可通过参数化函数表示，当策略以函数形式表示时，可通过优化特定标量指标来获得最优策略，这种方法称为策略梯度。 策略梯度方法具有诸多优势。例如，它能够更高效地处理大规模的状态/动作空间；具备更强的泛化能力，因而在样本利用率上也更为高效。
本章核心是掌握下面表格
目录
-
从表格到标量目标函数
-
评估指标 1：Average state value
-
评估指标 2: Average one-step reward
-
关于评估指标（metrics）的几点说明
-
Metric的另一种形式
一. 从表格到标量目标函数
前面学习的 Sarsa 和 Q-learning 均属于表格型强化学习，其中策略直接存储在状态-动作对应的条目中。最优策略被定义为：在所有状态上，其状态价值函数均不劣于其他任何策略的价值函数，这本质上是多个标量间的联合比较。
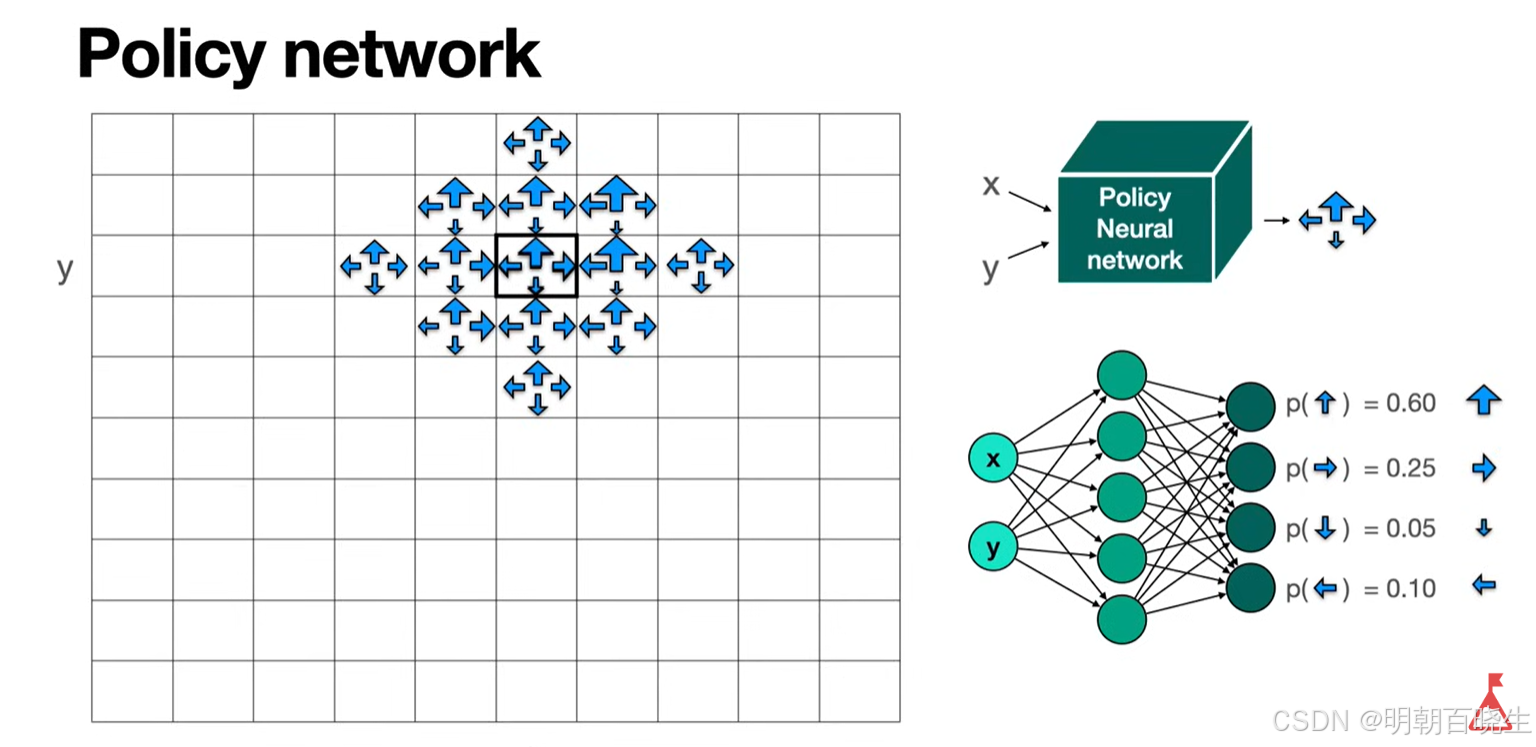
在函数逼近方法中，策略由参数（如神经网络权重）参数化为 ，策略空间连续且庞大，无法逐一比较各状态价值。此时，须定义一个单一、可微的标量目标函数 J(θ)，以整体评估策略
的优劣。
两种表示方法的差异：
1. 最优策略定义
- 表格形式：使每个状态价值最大化的策略。
- 函数形式：使某个标量指标最大化的策略。
2.策略更新方法
- 表格形式：直接修改表格中的策略条目。
- 函数形式：通过调整参数θ进行更新。
3. 动作概率获取
- 表格形式：直接查表获取动作概率。
- 函数形式：输入状态-动作对(s, a)计算概率，或输入状态输出动作概率分布。
二、评估指标一：Average state value
第一个指标是平均状态价值(简称平均值).其定义为
其中 d(s)为状态 s 的权重，满足对任意 有
，且
。
因此可将 解释为状态的概率分布,此时该指标可写为
d可分为两种情况：
1. 分布 d 与策略 无关
记 d 为 ，记指标为
以表明分布与策略独立。
1 所有状态同等重要:
为一个标量。
2 仅关注特定状态
2. 分布 d 依赖于策略
此时常取d 为策略
此时常取d为策略下的稳态分布，满足基本性质：
其中P为状态转移概率矩阵。
稳态分布反映了策略下MDP的长期行为：频繁访问的状态权重更高，反之权重更低。
状态价值的加权平均值J(θ)由参数θ决定，目标为寻找最优参数θ*以最大化J(θ)。
三 评估指标二: Average one-step reward
第二个度量是单步平均奖励（average one-step reward）具体定义为：
其中 是稳态分布，而策略的即时奖励
即时奖励为
本质上是一种递归求解的思想如下图
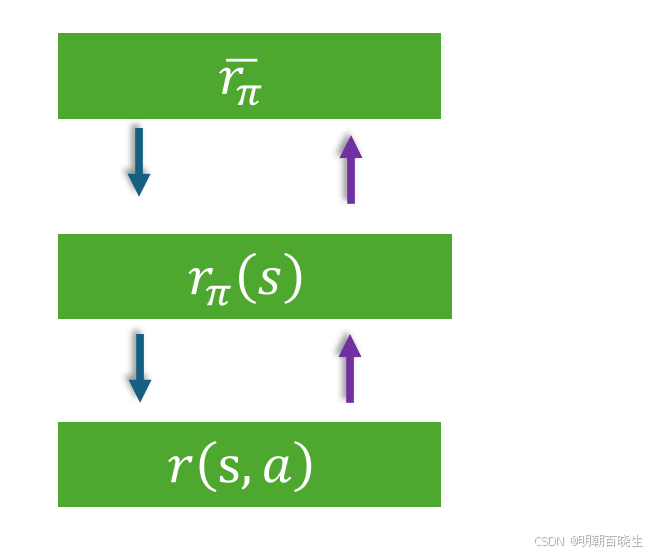
在强化学习中，上述等式还有一个等价定义：
**1：**假设我们遵循某个给定的策略 π，与环境交互生成一条轨迹（trajectory）。
2:计算该轨迹的平均单步奖励（average single-step reward），即：
avarage single-step reward
3随着时间步数 k 不断增大，根据马尔可夫性质（Markov property）及平稳性假设，初始状态 s0对长期平均奖励的影响将趋于消失。
四、关于评估指标（metrics）的几点说明
-
说明一：评估指标是策略的函数
-
评估指标 **
-
不同的策略会产生不同的评估指标值
-
-
说明二：关于评估指标的定义
-
一个复杂之处在于：评估指标可以定义在无折扣情况 下（其中 γ=1），也可以定义在折扣情况下（其中 0≤γ<1）
-
无折扣情况较为复杂
-
我们仅考虑折扣情况
-
-
说明三：关于评估指标的直观理解
-
直观上，折扣的总奖励 （γ=1）更注重长期回报，因为它考虑所有步骤的累计奖励
-
无折扣情况 （γ<1）则更短视，因为它更强调即时奖励
-
实际上，这两种形式在数学上是等效的（可通过适当转换证明）
-
四、Metric的另一种形式
前面我们学习了metric 的两种方式
公式（2）还有另外一种形式
- 它从初始状态分布出发，生成一条完整轨迹。
2 沿该轨迹计算累积奖励的均值，即可得到该度量的估计值
由此可知，该度量与平均奖励（average reward）等价
https://jonathan-hui.medium.com/rl-policy-gradients-explained-9b13b688b146https://www.youtube.com/watch?v=e20EY4tFC_Q