摘要
今日学习涵盖CFD仿真全流程，从前处理（几何定义、网格生成、边界与物理模型设置）到求解（稳态求解器配置、离散格式与收敛控制），再到后处理（监测点设置与报告生成），完整实践了仿真项目的设置、计算与结果验证。
Abstract
Today's learning covers the complete workflow of CFD simulation, from preprocessing (geometry definition, mesh generation, boundary and physical model setup) to solving (steady-state solver configuration, discretization schemes, and convergence control), and finally to post-processing (monitoring point setup and report generation). It involves the full practice of setting up, computing, and verifying a simulation project.
仿真流体Fluent：
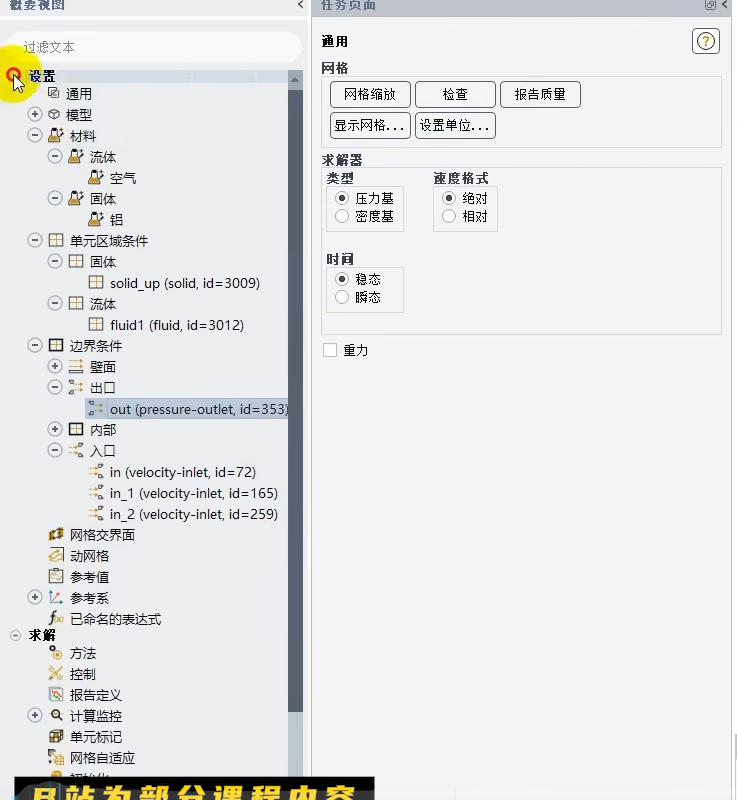
共同展示了CFD（计算流体力学）仿真在软件中进行物理模型与边界条件完整设置的核心框架。它们不是两个独立的部分，而是一个连贯工作流程中不同侧重点的体现：第一张图定义了仿真的"骨架"与"规则"，第二张图则提供了填充和丰富这个骨架的"血肉"与"工具"。
- 核心骨架搭建与基础规则定义
第一张图是仿真项目的总控制台和清单界面。它通过树状结构，系统化地确立了仿真的基础架构：
求解器与时间设定：选择了压力基（Pressure-Based）、绝对（Absolute） 速度格式的稳态（Steady） 求解器。这表明您要模拟的是一个不随时间变化的、不可压缩或弱可压缩的流动。同时，未启用重力，确定了基本的物理环境。材料定义：明确了计算中涉及的物质是空气（流体） 和铝（固体）。这是进行任何传热或共轭传热分析的前提。计算域与边界条件：这是最关键的部分。您将计算域清晰地划分为固体区域（solid_up） 和流体区域（fluid1），并为它们分配了材料。在边界条件中，您设置了一个压力出口（entire） 和三个独立的速度入口（in, in_1, in_2）。这共同定义了一个经典的多进口、单出口的内部流动场景，流体与固体之间存在相互作用。
- 物理细节丰富与高级模型启用
第二张图是物理现象和高级功能的"武器库"或"扩展面板"。它允许您在第一步搭建的骨架上，激活更复杂的物理过程和模型。
物理模型激活：界面中部的"模型"区域列出了可启用的高级物理模型，如能量方程（传热）、粘性模型（湍流）、辐射、多相流、组份输运（化学反应）、离散相（颗粒追踪） 等。您可以根据需要勾选，例如打开"能量"来模拟温度场，选择"粘性"中的k-epsilon模型来模拟湍流。
详细参数配置：点击每个模型（如"粘性..."），会弹出类似之前讨论过的详细设置窗口，供您选择具体的子模型和参数。
材料与区域深度定制：右侧的"材料"和"区域"选项，允许您创建新材料或为已定义的区域（如 solid_up或 fluid1）赋予更特殊的属性（如多孔介质、自定义源项等）。
CFD仿真的设置是一个从宏观到微观、从框架到细节的递进过程。第一张图完成项目的基础架构与全局规则制定，相当于绘制了施工蓝图和材料清单；第二张图则根据蓝图，选择具体的施工工艺和高级材料（物理模型），将简单的流动问题拓展为可能包含传热、湍流、化学反应等多物理场耦合的复杂仿真。两者紧密结合，缺一不可。
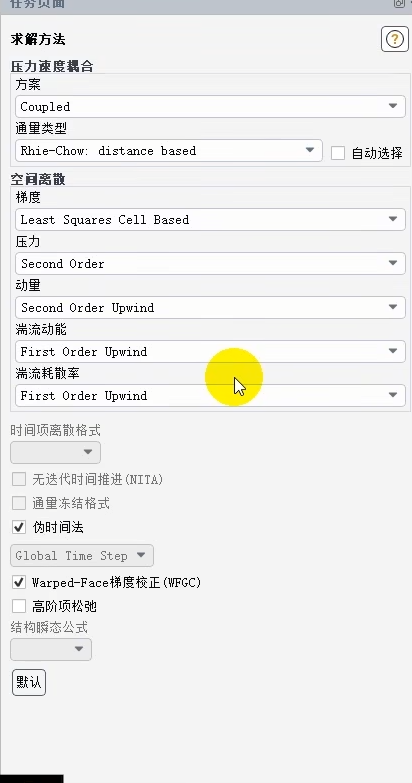
选择的 "Coupled" 压力-速度耦合方案，是一种强耦合算法，将动量方程和连续性方程联立求解。它比常用的 "SIMPLE" 系列算法更稳定、收敛更快，尤其适合可压缩流、强体积力（如浮力）和网格质量不佳的情况，但会占用更多内存。
在空间离散格式上，为压力和动量这两个最关键变量选择了二阶精度，这能显著减少数值扩散，获得更精确的结果。然而，对于湍流动能和耗散率这两个湍流模型变量，您选择了一阶迎风格式。这是一种常见的做法，因为一阶格式虽然精度低、数值扩散大，但具有绝对的稳定性，可以确保湍流方程在迭代初期不会发散，待流场初步稳定后，可以再尝试切换到二阶格式以提高精度。
其他关键设置包括："伪时间法" 用于稳态计算，通过引入虚拟的时间步来加速收敛；"基于最小二乘法的单元梯度" 是计算梯度最常用的方法；"基于距离的Rhie-Chow插值" 是防止非交错网格（即所有变量存储在细胞中心）出现压力振荡的标准技术；而"扭曲面梯度校正" 则是在网格质量不高时，提高梯度计算精度的重要选项。
总而言之，这套设置是一套偏向于稳健和实用的工程化配置：用耦合算法和伪时间法保障收敛效率，为主流变量使用二阶格式保证核心精度，同时用一阶格式稳住复杂的湍流方程，再辅以必要的校正技术来应对复杂的真实网格。
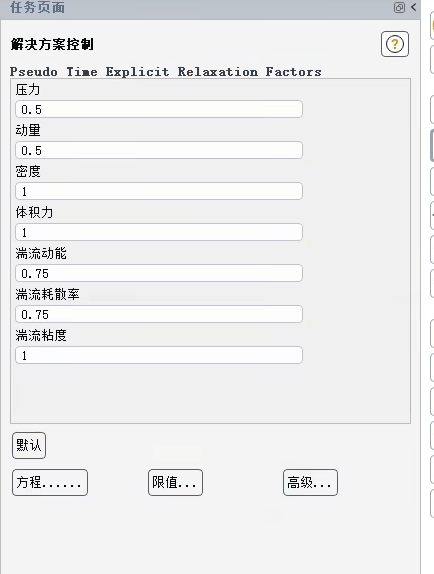
这些参数是显式伪时间推进法中的关键，通过控制每个物理量在迭代步中的更新幅度，在计算稳定性与收敛速度之间进行权衡。
各因子取值含义如下：
压力、动量 (0.5)：设置为中度松弛（小于1），是最常用的保守策略。这能有效阻尼压力-速度耦合中常见的高频振荡，防止计算发散，是保证稳态问题稳健收敛的关键。
湍流动能、湍流耗散率 (0.75)：采用比动量稍强的松弛因子，旨在适度加速这两个湍流变量的收敛，因为它们通常收敛较慢，但过大的步长（接近1）易导致不稳定。
密度、体积力、湍流粘度 (1.0)：采用完全松弛（即直接采用计算值）。通常表明在当前问题（如不可压或密度变化不大、无强体积力场）中，这些变量对稳定性的影响较小，采用最大步长以追求最快的收敛速度。
此设置是一套典型的、偏向稳健的工程配置：通过对关键变量（压力、动量）进行适度"刹车"（松弛），优先保证求解稳定；同时对次要变量采用更大甚至完全的步长，以兼顾效率。用户可通过底部的"方程..."等按钮进行更精细的全局或分方程调整。
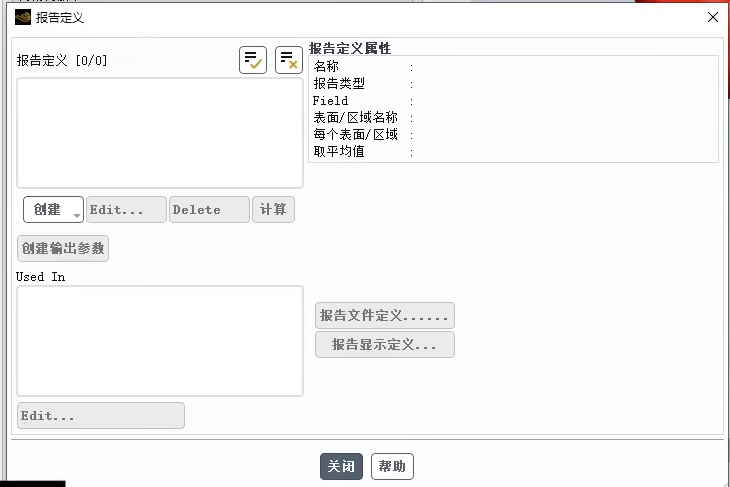
其核心功能是允许用户系统地定义、计算并输出在仿真中需要重点关注和记录的特定物理量数据，是实现仿真量化分析与自动化的重要工具。
界面上方的"报告定义属性"表格是核心区域，用户需要在此填写每个监控报告的具体参数：
名称：为该报告定义一个易于识别的标签。报告类型：选择要监控的物理量类型，例如力、力矩、流量、面积加权平均值、顶点平均值等。Field：指定报告类型对应的具体物理场变量，如选择报告类型为"力"后，再在此处选择是计算压力、粘性力还是总的力。表面/区域名称：指定计算该物理量的几何位置，例如特定的入口面、出口面、壁面或整个流体域。
每个表面/区域 & 取平均值：这些选项决定如何汇总数据，例如是对列表中的每个面分别报告，还是将所有面的数据合并后给出一个总值或平均值。
下方的按钮组提供了完整的工作流：
创建/Edit.../Delete：用于管理报告定义的列表。
计算：可立即基于当前设置计算并显示报告值，用于快速检查。
创建输出参数：这是高级且关键的功能，它允许将定义好的报告（如某个面的总阻力）转化为一个可以在优化设计、参数化扫描或与其他软件耦合时使用的输出变量。
报告文件/显示定义：用于设置报告的输出格式（如写入文本文件）和显示样式（如在控制台如何显示）。
此界面将用户从海量的仿真结果数据中解放出来，通过预先定义，可以自动、精准地提取关键性能指标（KPIs），并为进一步的自动化分析、优化和报告生成奠定基础。它体现了现代CFD软件从"提供结果"到"提供答案"的重要转变。
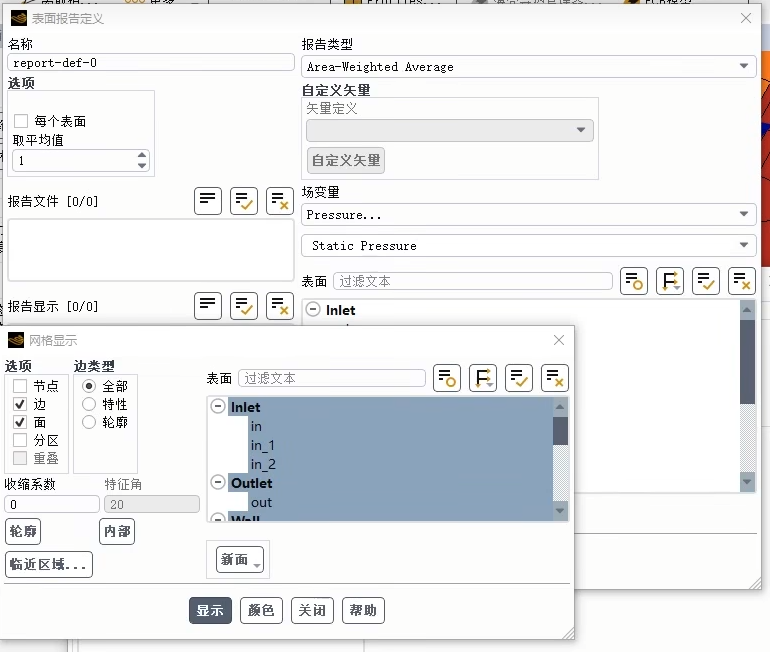
其核心目的是从仿真结果中自动提取并计算特定表面的关键物理量数据，实现从可视化定性分析到数据定量分析的转变。
界面的逻辑可分为左右两部分。左侧是定义区，用户在此创建和配置报告：
核心定义：你需要为报告命名，并选择报告类型。这里展示的类型是"面积加权平均 (Area-Weighted Average)"，这是计算诸如一个面上平均压力、平均温度等物理量的最常用方法。
变量与对象：你选择需要计算的场变量（例如 Static Pressure静压），并指定计算的表面对象（例如 Inlet入口面）。你可以直接在下方的"表面"列表中勾选，或在"网格显示"区点选图形来指定。
高级设置："选项"中的"自定义矢量"允许你定义矢量（如速度方向），用于计算流量、法向应力等与方向相关的物理量。底部的"报告文件"用于将计算结果自动输出到文本文件。
右侧是选择与确认区，帮助你精准选取目标表面：
"网格显示"面板：这里以列表形式列出了模型中所有已命名的表面（如Inlet, Outlet）。你可以通过勾选来高亮显示它们，确保你选择的是正确的表面。
显示控制：通过勾选"节点"、"边"、"面"等选项，可以控制这些几何元素在图形窗口中的显示与隐藏，辅助你查看和选择。"轮廓"和"特征角"等设置可以调整表面的显示效果。
此界面将手动"看图读数"的过程自动化了。通过它告诉软件："请计算在'入口'这个表面上，'静压'这个物理量的面积加权平均值，并把结果记录下来。" 这是生成性能指标、进行参数对比和撰写仿真报告的关键步骤。
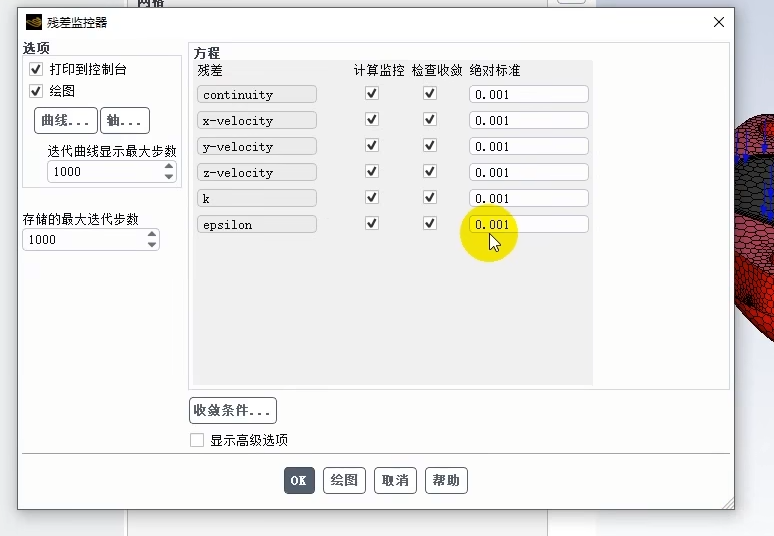
残差是衡量每次迭代后控制方程（如连续性方程、动量方程）不平衡量的指标，是判断计算是否收敛的核心依据。
已经为几个关键方程的收敛设定了绝对标准（Absolute Criteria） 为 0.001。这意味着当这些方程的残差（不平衡量）降低到0.001以下时，求解器将认为它们已经收敛。勾选了 "检查收敛" ，意味着求解器会依据此标准自动判断。同时，勾选了 "绘图" ，这能让残差随迭代步下降的曲线实时显示在图形窗口，这是最直观的监控方式。
界面中其他重要设置包括：
方程列表：列出了所有被监控的方程（连续性、X/Y/Z方向速度、湍流动能k、湍流耗散率epsilon）。您可以单独为每个方程设置是否监控、是否检查收敛以及收敛标准。
迭代显示设置："迭代曲线显示最大步数" 和 "存储的最大迭代步数" 都设为1000，这控制了曲线图上显示和软件内部保留的历史数据长度。
输出与高级选项："打印到控制台" 会将残差值输出到文本窗口；"收敛条件..."和"显示高级选项"提供了更精细的收敛判断设置入口。
此界面是您监控求解过程、确保结果可靠性的"仪表盘"。通过合理设置收敛标准（如您设定的0.001）并开启绘图，您可以直观地观察计算是否稳步趋于收敛（残差曲线持续平稳下降至标准以下），从而判断解的可信度，或及时发现问题（如残差曲线振荡、居高不下）并调整计算设置。
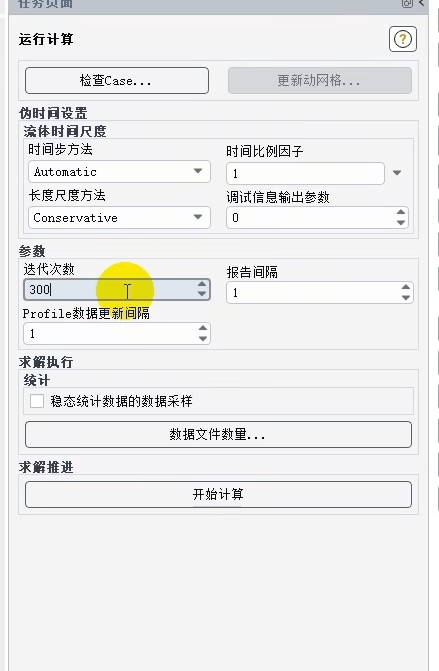
CFD求解器在执行稳态计算前的最终运行参数配置界面，是连接"设置"与"计算结果"的最后控制台。其主要功能是定义求解的推进方式、监控频率和停止条件，确保计算高效、稳定地进行。
界面按功能可分为几个核心部分：
-
计算前检查与更新："检查Case..."用于验证所有设置（如边界条件、材料属性）是否完整且自洽；"更新动网格..."则是在使用动网格或变形网格时才需启用。
-
稳态求解的稳定性控制（伪时间设置）：这是稳态计算的核心加速与稳定机制。
流体时间尺度：控制方程中"伪时间"步的物理尺度。时间步方法：设置为"Automatic (自动)"，表示软件会根据流场局部条件（如网格尺寸、流速）自动计算并调整每个单元的时间步长，这是最常用且稳健的方法。长度尺度方法：设置为"Conservative (保守)"，意味着在计算特征长度（如用于决定时间步的网格尺度）时采用更保守（通常更小）的估计，以增强计算稳定性，尤其适用于复杂网格或初始流场不佳的情况。时间比例因子：全局缩放自动计算出的时间步长，因子小于1会减小时间步，使计算更稳定但更慢；大于1则相反，用于加速收敛。
-
计算过程控制（参数）：
迭代次数 (300)：这是求解的停止条件之一。计算将进行最多300步迭代，若在此之前达到收敛标准（如残差降至设定值），则会提前停止。报告间隔 (1)：设定在控制台窗口每1个迭代步输出一次残差等收敛信息，使用户可以实时紧密监控计算进程。Profile数据更新间隔 (1)：设定每1个迭代步更新一次所有已定义的监测点、表面报告等数据，确保监控数据的实时性。
-
数据输出设置（求解执行）：
稳态统计数据的数据采样：定义如何为稳态计算（即使是非定常的统计稳态）收集时间平均统计数据。数据文件数量...：设置结果文件自动保存的频率和数量，例如每100步保存一个备份文件，防止计算意外中断导致数据全部丢失。计算启动（求解推进）：完成所有设置后，点击"开始计算"按钮，求解器即按照上述配置开始迭代求解。
此界面是用户对计算过程进行"宏观调控"的最终步骤。通过合理设置"自动+保守"的伪时间步策略、足够的迭代步数（300）、紧密的监控间隔（1）和必要的数据保存，可以在追求计算效率的同时，最大程度保障稳态求解过程的稳定与可控。
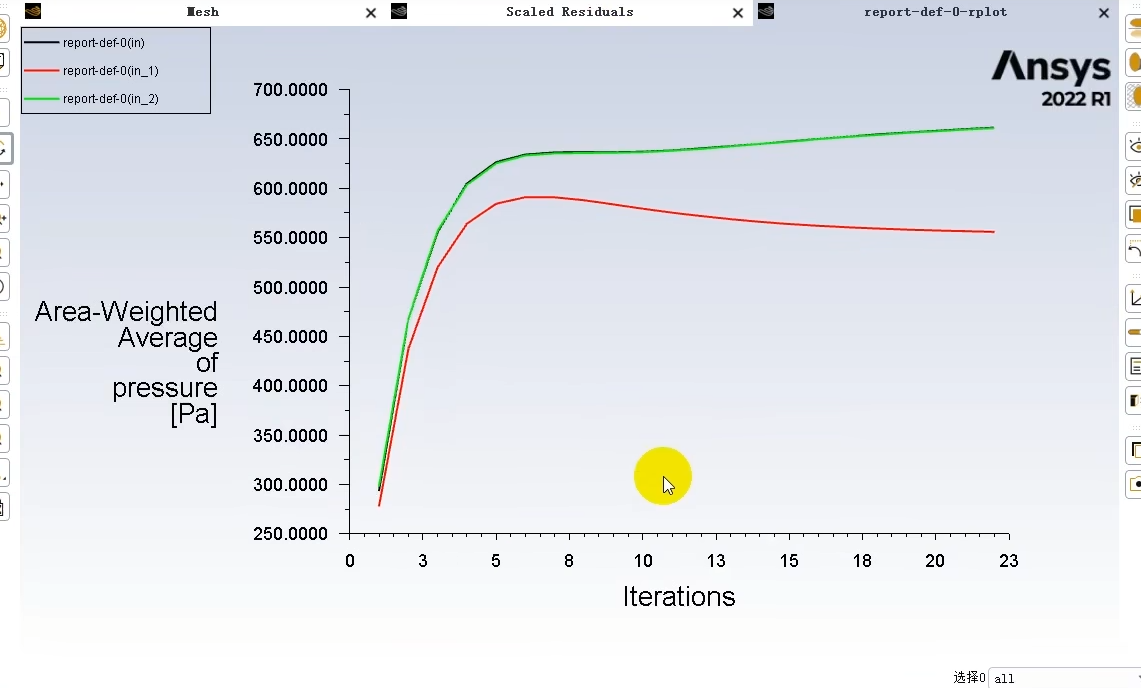此图是连接"求解设置"与"最终结果"的桥梁。它证明了计算正在有效进行并趋于稳定，同时也为您提供了关于流场初始状态的定量数据。为确保完全收敛，通常还需结合残差曲线（Scaled Residuals）共同判断，当所有监测量的变化和残差均降至可接受的低水平并保持平稳时，计算结果方可采信。