【February 组队学习【数学建模导论】~】

跳过绪论，

分为 教程实践 心得小记 教程链接🔗

教程实践

!git clone https://github.com/datawhalechina/intro-mathmodel.git

第1章 解析方法与几何模型

本章当中主要学习几何模型的相关知识

1.1 向量表示法与几何建模基本案例

1.1.1 几何建模的思想

三角函数 四点共圆 圆锥曲线 都回来了

1.1.2 向量表示与坐标变换

Python 中使用 NumPy 库来创建和操作向量 , coding

Python IDE推荐 PyCharm、
Visual Studio Code (VS Code) 建议搭配Jupyter Notebook食用

教程直接粘贴会空格出错

tips:先粘贴到CSDN再点击复制到VS Code中

import numpy as np

# 定义旋转角度（以弧度为单位）
alpha = np.radians(30)  # 绕 Z 轴旋转
beta = np.radians(45)   # 绕 Y 轴旋转
gamma = np.radians(60)  # 绕 X 轴旋转

# 定义旋转矩阵
R_x = np.array([[np.cos(alpha), -np.sin(alpha), 0],
                [np.sin(alpha), np.cos(alpha), 0],
                [0, 0, 1]])
R_y = np.array([[np.cos(beta), 0, np.sin(beta)],
                [0,1,0],
                [-np.sin(beta), 0, np.cos(beta)]])
R_z = np.array([[1, 0, 0],
                [0, np.cos(gamma), -np.sin(gamma)],
                [0, np.sin(gamma), np.cos(gamma)]])

# 总旋转矩阵
R = R_z @ R_y @ R_x

# 定义点P的坐标
P = np.array([1, 2, 3])

# 计算旋转后的坐标
P_rotated = R @ P

print("旋转后P点的坐标为:", P_rotated)
# 旋转后P点的坐标为: [3.39062937 0.11228132 1.57829826]

output

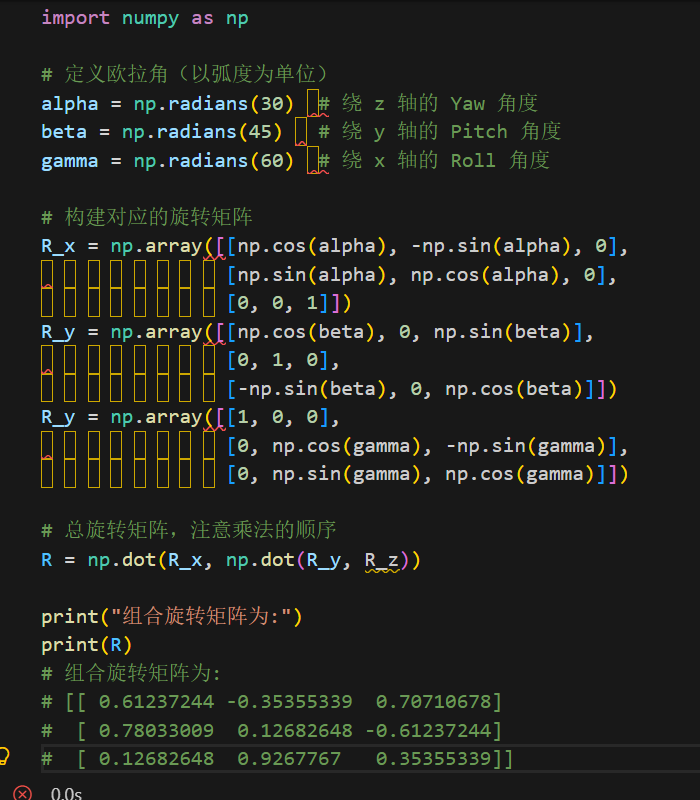
import numpy as np

# 定义欧拉角（以弧度为单位）
alpha = np.radians(30)  # 绕 z 轴的 Yaw 角度
beta = np.radians(45)   # 绕 y 轴的 Pitch 角度
gamma = np.radians(60)  # 绕 x 轴的 Roll 角度

# 构建对应的旋转矩阵
R_x = np.array([[np.cos(alpha), -np.sin(alpha), 0],
                [np.sin(alpha), np.cos(alpha), 0],
                [0, 0, 1]])
R_y = np.array([[np.cos(beta), 0, np.sin(beta)],
                [0, 1, 0],
                [-np.sin(beta), 0, np.cos(beta)]])
R_y = np.array([[1, 0, 0],
                [0, np.cos(gamma), -np.sin(gamma)],
                [0, np.sin(gamma), np.cos(gamma)]])

# 总旋转矩阵，注意乘法的顺序
R = np.dot(R_x, np.dot(R_y, R_z))

print("组合旋转矩阵为:")
print(R)
# 组合旋转矩阵为:
# [[ 0.61237244 -0.35355339  0.70710678]
#  [ 0.78033009  0.12682648 -0.61237244]
#  [ 0.12682648  0.9267767   0.35355339]]

output

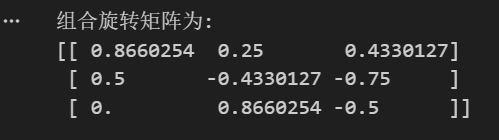
1.2 Numpy 与线性代数

Python中最强大的科学计算库之一：NumPy

线性代数不仅是理解数据结构、解决数学问题的基础，也是计算机图形学、机器学习等高级领域不可或缺的工具。NumPy库在这里扮演了至关重要的角色，它为我们提供了一个高效、便捷的平台来处理数值计算和线性代数运算。

1.2.2 利用Numpy进行线性代数基本运算

在NumPy中，我们可以利用数组的广播机制来进行各种线性代数运算。NumPy也提供了计算矩阵的转置、行列式、逆矩阵等常见操作的函数

import numpy as np
# 创建向量
vector = np.array([1, 2, 3])
# 创建矩阵
matrix = np.array([[1, 2, 3],
                   [4, 5, 6],
                   [7, 8, 9]])

import numpy as np

# 数量乘法示例
scalar = 5
scaled_vector = scalar * vector
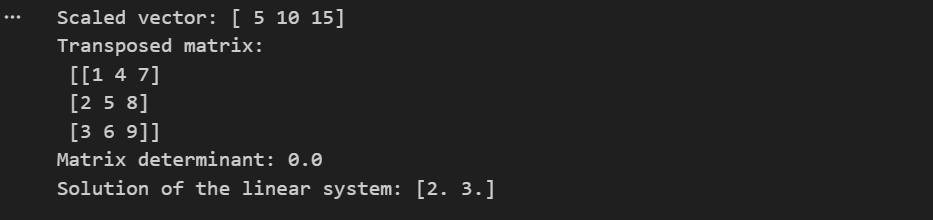
print("Scaled vector:", scaled_vector)
# Scaled vector: [ 5 10 15]

# 矩阵的转置示例
transposed_matrix = matrix.T
print("Transposed matrix:\n", transposed_matrix)
# Transposed matrix:
# [[1, 4, 7]
#  [2, 5, 8]
#  [3, 6, 9]]

# 计算行列式示例
matrix_determinant = np.linalg.det(matrix)
print("Matrix determinant:", matrix_determinant)
# Matrix determinant: 0.0

# 求解线性方程组示例
A = np.array([[3, 1], [1, 2]])
b = np.array([9, 8])
solution = np.linalg.solve(A, b)
print("Solution of the linear system:", solution)
# Solution of the linear system: [2. 3.]

output

1.4.1 多项式的构造与运算

import numpy as np
import matplotlib.pyplot as plt

# 示例数据：x值和对应的y值（可能含有噪声）
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([0, 0.8, 0.9, 0.1, -0.8, -1])

# 指定多项式的度数
deg = 2

# 使用numpy.polyfit进行多项式拟合
# 返回的coeffs是多项式的系数，从最高次项到常数项
coeffs = np.polyfit(x, y, deg)

# 使用numpy.poly1d创建多项式对象（可选）
p = np.poly1d(coeffs)

# 打印拟合得到的多项式
print("拟合得到的多项式:", p)

# 使用拟合得到的多项式进行预测（可选）
x_fit = np.linspace(min(x), max(x), 100)  # 生成一系列x值用于绘图
y_fit = p(x_fit)  # 计算对应的y值

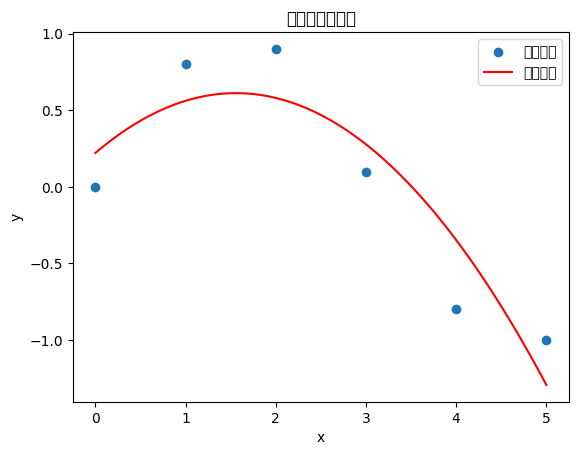
# 绘图展示原始数据和拟合曲线
plt.scatter(x, y, label='原始数据')
plt.plot(x_fit, y_fit, color='red', label='拟合曲线')
plt.xlabel('x')
plt.ylabel('y')
plt.title('多项式拟合示例')
plt.legend()
plt.show()

多项式拟合的详细示例

.............................................由于 task1打卡 第6章起 且13 截止 ............跳过 ............

第6章 数据处理与拟合模型

数据科学是统计学、计算机科学和领域知识的交叉学科" 如图

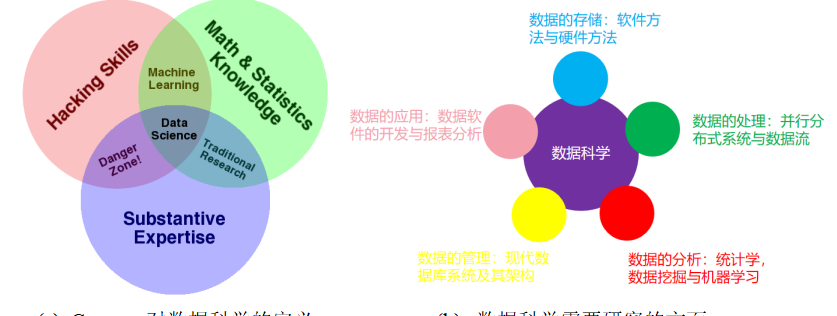
数学基础，也需要计算机基础，但在解决实际工程问题的时候需要特定的工程背景

大数据科学研究的不仅仅是数据分析 agree

（1）Python创建一个数据框DataFrame：
import pandas as pd
import numpy as np
data = {'animal': ['cat', 'cat', 'snake', 'dog', 'dog', 'cat',
'snake', 'cat', 'dog', 'dog'],
        'age': [2.5, 3, 0.5, np.nan, 5, 2, 4.5, np.nan, 7, 3],
        'visits': [1, 3, 2, 3, 2, 3, 1, 1, 2, 1],
        'priority': ['yes', 'yes', 'no', 'yes', 'no', 'no', 'no',
 'yes', 'no', 'no']}

labels = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j']
df = pd.DataFrame(data)
（2）显示该 DataFrame 及其数据相关的基本信息：
df.describe()
（3）返回DataFrame df 的前5列数据：
df.head(5)
（4）从 DataFrame `df` 选择标签列为 `animal` 和 `age` 的列
df[['animal', 'age']]
（5）在 `[3, 4, 8]` 行中，列为 `['animal', 'age']` 的数据
df.loc[[3, 4, 8], ['animal', 'age']]
（6）选择列为`visits`中等于3的行
df.loc[df['visits']==3, :]
（7）选择 `age` 为缺失值的行
df.loc[df['age'].isna(), :]
（8）选择 `animal` 是cat且`age` 小于 3 的行
df.loc[(df['animal'] == 'cat') & (df['age'] < 3), :]
（9）选择 `age` 在 2 到 4 之间的数据（包含边界值）
df.loc[(df['age']>=2)&(df['age']<=4), :]
（10）将 'f' 行的 `age` 改为 1.5
df.index = labels
df.loc[['f'], ['age']] = 1.5
（11）对 `visits` 列的数据求和
df['visits'].sum()
（12）计算每种 `animal` `age` 的平均值
df.groupby(['animal'])['age'].mean()

np.nan 是一个特殊的浮点数值，代表了"Not a Number"（非数字）。这个值通常用于表示缺失或无效的数据

数据的规约

统计分析通常在做"为什么"的任务，机器学习通常在做"预测未来"的任务。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
import seaborn as sns
from IPython.display import display
import statsmodels.api as sm

# 加载数据
gpa1 = pd.read_stata('./data/gpa1.dta')  # 从 Stata 数据文件中加载数据

# 在数据集中提取自变量（ACT为入学考试成绩、hsGPA为高考成绩）
X1 = gpa1.ACT  # 提取ACT成绩作为自变量
X2 = gpa1[['ACT', 'hsGPA']]  # 提取ACT和hsGPA成绩作为自变量

# 提取因变量
y = gpa1.colGPA  # 提取大学成绩作为因变量

# 为自变量增添截距项
X1 = sm.add_constant(X1)  # 为X1添加截距项
X2 = sm.add_constant(X2)  # 为X2添加截距项
display(X2)  # 显示添加截距项后的X2

# 拟合两个模型
gpa_lm1 = sm.OLS(y, X1).fit()  # 使用普通最小二乘法拟合模型1（仅ACT）
gpa_lm2 = sm.OLS(y, X2).fit()  # 使用普通最小二乘法拟合模型2（ACT和hsGPA）

# 输出两个模型的系数与对应p值
p1 = pd.DataFrame(gpa_lm1.pvalues, columns=['pvalue'])  # 提取模型1的p值
c1 = pd.DataFrame(gpa_lm1.params, columns=['params'])  # 提取模型1的系数
p2 = pd.DataFrame(gpa_lm2.pvalues, columns=['pvalue'])  # 提取模型2的p值
c2 = pd.DataFrame(gpa_lm2.params, columns=['params'])  # 提取模型2的系数

# 显示模型1的系数和p值
display(c1.join(p1, how='right'))  
# 显示模型2的系数和p值
display(c2.join(p2, how='right'))

最小二乘法（英文名：ordinary least squares），又称最小平方法

在机器学习中，对数据集的特征进行编码和缩放是预处理步骤中非常重要的一部分。这些步骤有助于提升模型的性能，特别是当数据集中的特征具有不同的量纲或包含分类变量时。以下是几种常见的方法，包括使用sklearn库来实现它们。

【心得体会】 ：工欲善其事必先利其器，github教程由markdown组成，直接git clone后，配置VS CodeMarkDown编辑器插件，高亮文本，高效阅读比ctrl+c ctrl+v 方便太多了。DataFrame

df.head(5) 想起和鲸的课程😀

统计分析通常是为了回答"为什么"的问题，即解释数据背后的因果关系。在学习统计分析的过程中，我们经常会重新审视一些基础概念，如普通最小二乘法（OLS）和最大似然估计（MLE）。这些方法在数据分析中扮演着核心角色，帮助我们从数据中提取有用的信息。

普通最小二乘法（OLS）是一种用于估计线性回归模型参数的方法，它通过最小化残差的平方和来找到最佳拟合线。最大似然估计（MLE）则是一种更通用的参数估计方法，它通过最大化似然函数来估计模型参数。在物理学中，最大似然估计与最概然分布的概念有相似之处，在统计物理中，最概然分布描述了在给定条件下系统最可能出现的状态。

概率和似然的概念在统计分析中也非常关键。概率描述了在已知参数的情况下，随机变量的输出结果；而似然则用来描述在已知随机变量输出结果的情况下，未知参数的可能取值。这种从结果倒推参数的方法在许多领域都有广泛应用，例如在机器学习中，我们经常使用最大似然估计来优化模型参数，从而更好地拟合数据。

通过这些工具和方法，我们可以更深入地理解和分析数据，从而更好地回答那些"为什么"的问题。

tips：

十分喜欢VS Code，私以为配置好后的VS Code不逊色于任何一款MarkDown编辑器，当然，如果觉得自己配置太麻烦的话，也可以直接使用上述编辑器或者Typora这款编辑器

安装markdown editor插件，实现加粗等

改变文字颜色

可以使用内联样式中的color属性来改变文字颜色。

例如：

<span style="color: red;">这是红色的文字。</span>

• 高亮文本
  Markdown原生并不支持文本高亮功能，但你可以通过内联样式结合HTML标签来实现这一效果。
  例如：

  这是黄色高亮的文本，
  这是粉色高亮的文本，
  这是蓝色高亮的文本，
  这是绿色高亮的文本。

【教程地址】

https://github.com/datawhalechina/intro-mathmodel

http://www.datawhale.cn/learn/summary/85

代码实操有https://datawhalechina.github.io/scientific-computing/#/