文章目录
- [1 问题描述](#1 问题描述)
- [2 研究分析](#2 研究分析)
- [3 建立系统的数学模型](#3 建立系统的数学模型)
- [4 Python仿真程序](#4 Python仿真程序)
- [5 仿真结果](#5 仿真结果)
1 问题描述
RLC电路是电子学中最基础也最重要的电路系统之一。它由电阻、电感和电容三大无源元件构成,因能产生振荡和谐振现象,常用于滤波、选频、阻抗匹配等。
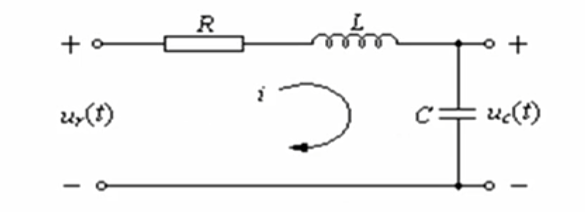
如图所示是RLC电路系统,取 L = 1 H , C = 1 F L=1H,C=1F L=1H,C=1F,考虑系统在单位阶跃输入情况下,讨论系统不产生振荡时电阻R的取值,其中R的取值不大于 0.1 Ω 0.1Ω 0.1Ω。
2 研究分析
要求研究的问题是:当 L = 1 H , C = 1 F L=1H,C=1F L=1H,C=1F时,分析系统在输入作用 u r ( t ) = 1 ( t ) u_r(t)=1(t) ur(t)=1(t) 的作用下,要使响应不发生振荡,通过计算机仿真研究 R R R应在什么范围内取值。
3 建立系统的数学模型
(1)根据电学中的基尔霍夫定律,可写出原始方程:
L d i ( t ) d t + R i ( t ) + 1 C ∫ i ( t ) d t = u r ( t ) (1.1) L\frac{di(t)}{dt} + Ri(t)+\frac{1}{C}\int i(t)dt=u_r(t) \tag{1.1} Ldtdi(t)+Ri(t)+C1∫i(t)dt=ur(t)(1.1)
(2)式 ( 1.1 ) (1.1) (1.1) 中 i i i 是中间变量,它与输出有如下关系:
u c ( t ) = 1 C ∫ i ( t ) d t (1.2) u_c(t) = \frac{1}{C} \int i(t)dt \tag{1.2} uc(t)=C1∫i(t)dt(1.2)
(3)消去式 ( 1.1 ) (1.1) (1.1)、式 ( 1.2 ) (1.2) (1.2)的中间变量 i i i后,便得输入与输出的微分方程式:
L C d 2 u c ( t ) d t 2 + R C d u c ( t ) d t + u c ( t ) = u r ( t ) (1.3) LC\frac{d^2 u_c(t)}{dt^2} + RC \frac{du_c(t)}{dt} + u_c(t) = u_r(t) \tag{1.3} LCdt2d2uc(t)+RCdtduc(t)+uc(t)=ur(t)(1.3)
(4)将式 ( 1.3 ) (1.3) (1.3)转换成状态方程及输出方程形式:
x 1 ˙ ( t ) x 2 ˙ ( t ) \] = \[ 0 1 − R L − 1 L C \] \[ x 1 ( t ) x 2 ( t ) \] + \[ 0 1 L C \] u r ( t ) u c ( t ) = \[ 1 0 \] \[ x 1 ( t ) x 2 ( t ) \] (1.4) \\begin{bmatrix} \\dot{x_1}(t) \\\\ \\dot{x_2}(t) \\end{bmatrix} = \\begin{bmatrix} 0 \& 1 \\\\ -\\frac{R}{L} \& -\\frac{1}{LC} \\end{bmatrix} \\begin{bmatrix} x_1(t) \\\\ x_2(t) \\end{bmatrix} + \\begin{bmatrix} 0 \\\\ \\frac{1}{LC} \\end{bmatrix} u_r(t) \\\\ u_c(t)=\\begin{bmatrix} 1 \& 0 \\end{bmatrix}\\begin{bmatrix} x_1(t) \\\\ x_2(t) \\end{bmatrix} \\tag{1.4} \[x1˙(t)x2˙(t)\]=\[0−LR1−LC1\]\[x1(t)x2(t)\]+\[0LC1\]ur(t)uc(t)=\[10\]\[x1(t)x2(t)\](1.4)
* 注:状态方程和输出方程的形式为:
d x d t = A x + B u y = C x + D u \\frac{dx}{dt}=Ax+Bu \\\\ y=Cx+Du dtdx=Ax+Buy=Cx+Du
其中, x x x是状态向量, u u u是控制向量, y y y是被测信号, A A A、 B B B、 C C C和 D D D是常数矩阵。
(5)将第(4)步转换成离散的状态方程及输出方程,用于计算仿真及编程:
\[ x 1 ( ( k + 1 ) T ) x 2 ( ( k + 1 ) T ) \] = \[ x 1 ( k T ) x 2 ( k T ) \] + \[ 0 1 − R L − 1 L C \] \[ x 1 ( k T ) x 2 ( k T ) \] T + \[ 0 1 L C \] u r ( k T ) T u c ( ( k + 1 ) T ) = x 1 ( ( k + 1 ) T ) (1.5) \\begin{bmatrix} x_1((k+1)T) \\\\ x_2((k+1)T) \\end{bmatrix} = \\begin{bmatrix} x_1(kT) \\\\ x_2(kT) \\end{bmatrix} + \\begin{bmatrix} 0 \& 1 \\\\ -\\frac{R}{L} \& -\\frac{1}{LC} \\end{bmatrix} \\begin{bmatrix} x_1(kT) \\\\ x_2(kT) \\end{bmatrix}T + \\begin{bmatrix} 0 \\\\ \\frac{1}{LC} \\end{bmatrix} u_r(kT)T \\\\ u_c((k+1)T)= x_1((k+1)T) \\tag{1.5} \[x1((k+1)T)x2((k+1)T)\]=\[x1(kT)x2(kT)\]+\[0−LR1−LC1\]\[x1(kT)x2(kT)\]T+\[0LC1\]ur(kT)Tuc((k+1)T)=x1((k+1)T)(1.5)
式中, T T T为采样周期。
* 连续方程离散化参考: