一、基础定义
| 表示 | 自由度 | 描述 | 优缺点 |
|---|---|---|---|
| 旋转矩阵 R | 3×3 → 3自由度 | 刚体旋转线性映射 | ✅ 直接乘点云/向量方便 ❌ 冗余、累积误差易破坏正交性 |
| 四元数 q = [w,x,y,z] | 4 → 3自由度 | 单位四元数表示旋转 | ✅ 紧凑、无奇异点、插值方便 ❌ 不直观,公式理解稍复杂 |
| 欧拉角 (roll, pitch, yaw) | 3 | 绕固定轴顺序旋转 | ✅ 直观角度表示 ❌ 万向节锁、插值不方便 |
二、旋转矩阵 ↔ 欧拉角
假设 ZYX 顺序(yaw-pitch-roll):
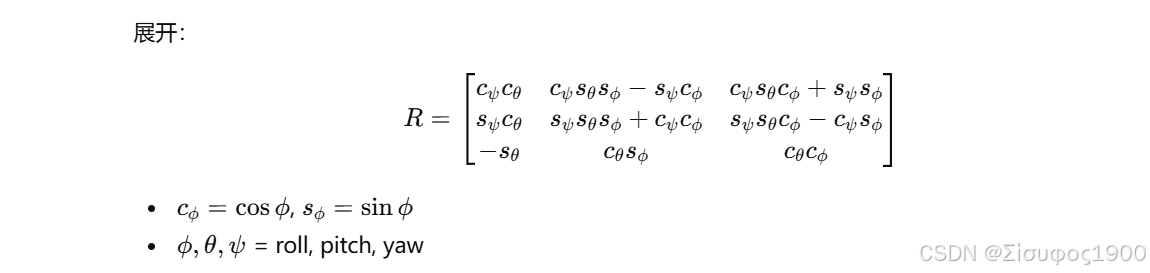
cpp
% 欧拉角 -> 旋转矩阵
phi = pi/6; theta = pi/4; psi = pi/3;
R = eul2rotm([psi,theta,phi]); % 默认 ZYX 顺序
disp(R)
0.3536 -0.5732 0.7392
0.6124 0.7392 0.2803
-0.7071 0.3536 0.6124
cpp
% 旋转矩阵 -> 欧拉角
eul = rotm2eul(R);
disp(rad2deg(eul)) % 转为角度显示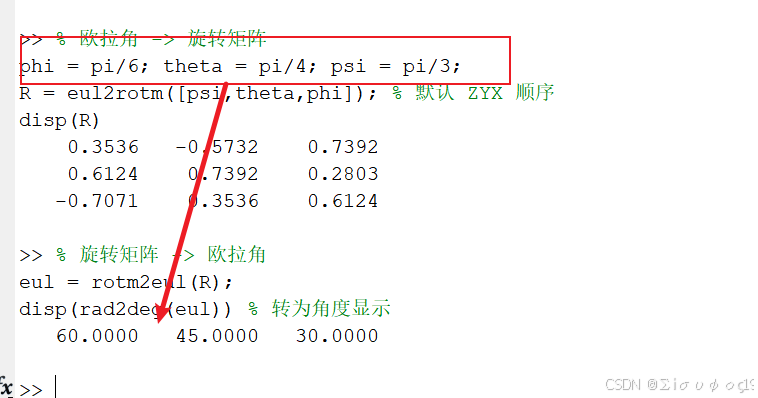
三、旋转矩阵 ↔ 四元数
-
四元数 q = [w, x, y, z]
-
旋转矩阵到四元数公式:
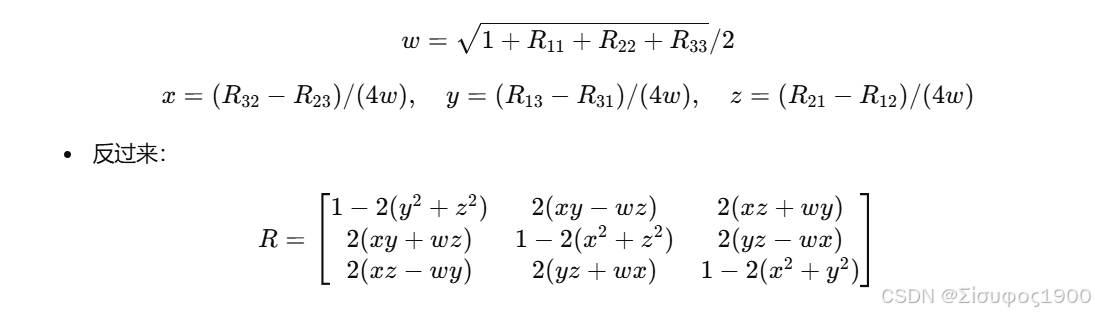
cpp
% 旋转矩阵 -> 四元数
q = rotm2quat(R); % 返回 [w x y z]
disp(q)
% 四元数 -> 旋转矩阵
R2 = quat2rotm(q);
disp(R2)
四、欧拉角 ↔ 四元数
-
欧拉角 → 旋转矩阵 → 四元数
cpp% 欧拉角 -> 四元数 q = eul2quat([psi,theta,phi]);
-
四元数 → 旋转矩阵 → 欧拉角
cpp% 四元数 -> 欧拉角 eul = quat2eul(q); disp(rad2deg(eul))
五、总结
1、示意图
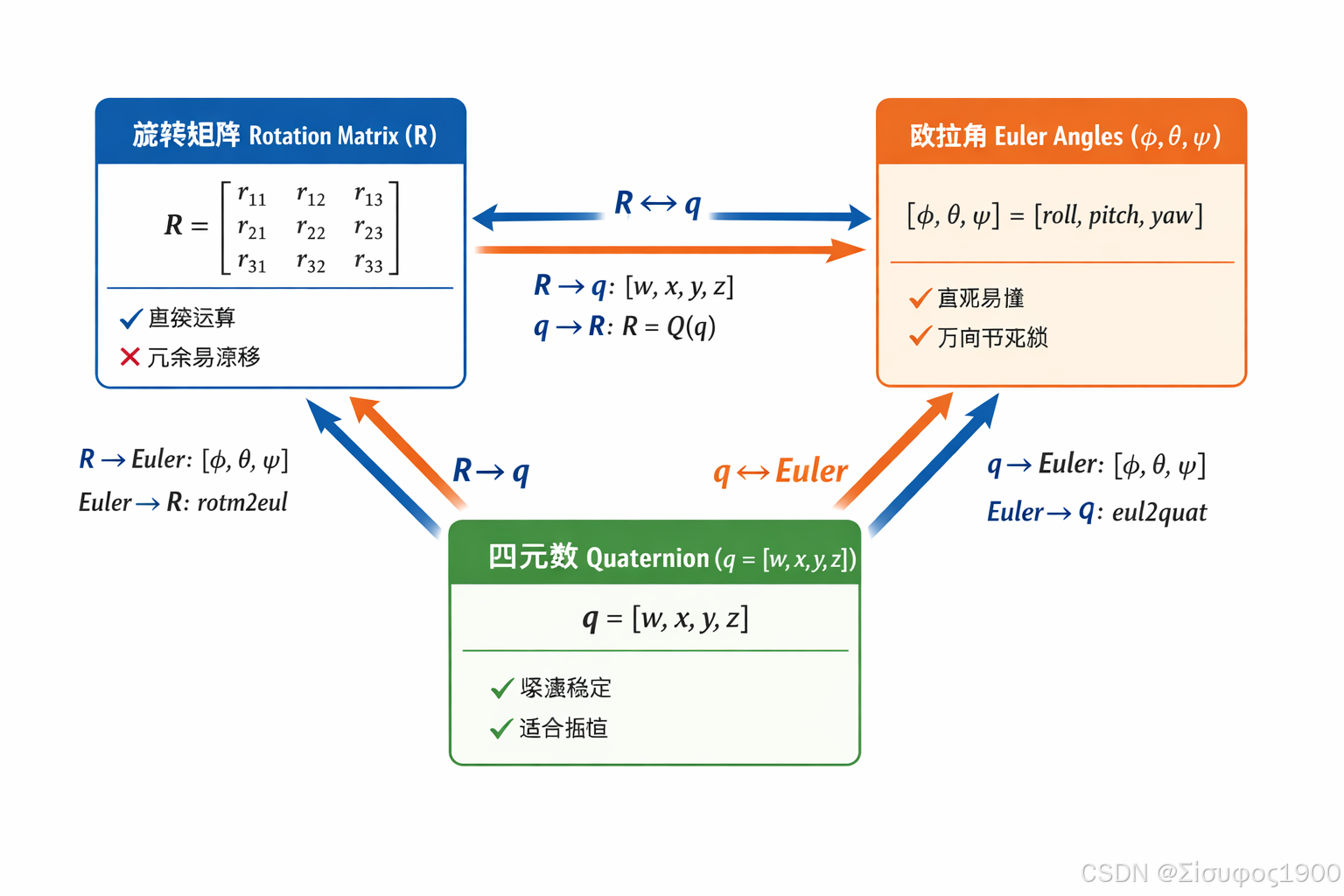
| 转换 | MATLAB 函数 |
|---|---|
| 欧拉角 → 旋转矩阵 | eul2rotm() |
| 旋转矩阵 → 欧拉角 | rotm2eul() |
| 旋转矩阵 → 四元数 | rotm2quat() |
| 四元数 → 旋转矩阵 | quat2rotm() |
| 欧拉角 → 四元数 | eul2quat() |
| 四元数 → 欧拉角 | quat2eul() |
2、问题
-
问:为什么四元数比欧拉角好?
✅ 因为四元数无万向节锁,可连续插值(SLERP),适合优化和控制。
-
问:为什么旋转矩阵要保持正交?
✅ 保持向量长度和正交性,否则会产生缩放或扭曲。
-
问:三者的转换注意什么?
✅ 顺序(ZYX vs XYZ)和单位四元数规范化。
-
问:ICP / Kabsch 用哪种表示?
✅ R(旋转矩阵)为主,用四元数优化也可,但旋转矩阵更直观。
旋转矩阵适合计算,四元数适合插值,欧拉角适合展示。