【计算机图形学中的四元数】2/2 Quaternions for Computer Graphics

Quaternions for Computer Graphics 计算机图形学中的四元数

文章目录

• [Quaternions for Computer Graphics 计算机图形学中的四元数](#Quaternions for Computer Graphics 计算机图形学中的四元数)
• • [7 3D旋转变换](#7 3D旋转变换)
  • [8 空间中的四元数](#8 空间中的四元数)

7 3D旋转变换

1. 平移某个点的矩阵 （使用齐次坐标）
   T t x , t y , t z = [ 1 0 0 t x 0 1 0 t y 0 0 1 t z 0 0 0 1 ] \mathbf{T}_{t_x,t_y,t_z} = \begin{bmatrix}1&0&0&t_x\\0&1&0&t_y\\0&0&1&t_z\\0&0&0&1 \end{bmatrix} Ttx,ty,tz= 100001000010txtytz1

2. 绕坐标轴旋转的矩阵
   R α , x = [ 1 0 0 0 cos ⁡ α − sin ⁡ α 0 sin ⁡ α cos ⁡ α ] R α , y = [ cos ⁡ α 0 sin ⁡ α 0 1 0 − sin ⁡ α 0 cos ⁡ α ] R α , z = [ cos ⁡ α − sin ⁡ α 0 sin ⁡ α cos ⁡ α 0 0 0 1 ] \begin{aligned} \mathbf{R}{\alpha,x}&= \begin{bmatrix}1&0&0\\0&\cos\alpha&-\sin\alpha\\0&\sin\alpha&\cos\alpha \end{bmatrix} \\ \mathbf{R}{\alpha,y}&=\begin{bmatrix}\cos\alpha&0&\sin\alpha\\0&1&0\\-\sin\alpha&0&\cos\alpha \end{bmatrix} \\ \mathbf{R}_{\alpha,z}&=\begin{bmatrix}\cos\alpha&-\sin\alpha&0\\\sin\alpha&\cos\alpha&0\\0&0&1 \end{bmatrix} \end{aligned} Rα,xRα,yRα,z= 1000cosαsinα0−sinαcosα = cosα0−sinα010sinα0cosα = cosαsinα0−sinαcosα0001

3. 绕某个偏置坐标轴旋转的矩阵

   • 原理：为了绕与其中一个笛卡儿轴平行的轴旋转，通常采用齐次坐标并平移要旋转的点，以便它可以绕原点旋转，然后以相等且相反的量平移回来，如

     x ′ y ′ z ′ 1 \] = T ( t x , t y , 0 ) R γ , z T ( − t x , − t y , 0 ) \[ x y z 1 \] \\begin{bmatrix}x'\\\\y'\\\\z'\\\\1 \\end{bmatrix} = \\mathbf{T}_{(t_x,t_y,0)}\\mathbf{R}_{\\gamma,z}\\mathbf{T}_{(-t_x,-t_y,0)}\\begin{bmatrix}x\\\\y\\\\z\\\\1 \\end{bmatrix} x′y′z′1 =T(tx,ty,0)Rγ,zT(−tx,−ty,0) xyz1

   R α , x , ( 0 , t y , t z ) = [ 1 0 0 0 0 cos ⁡ α − sin ⁡ α t y ( 1 − cos ⁡ α ) + t z sin ⁡ α 0 sin ⁡ α cos ⁡ α t z ( 1 − cos ⁡ α ) − t y sin ⁡ α 0 0 0 1 ] R α , y , ( t x , 0 , t z ) = [ cos ⁡ α 0 sin ⁡ α t x ( 1 − cos ⁡ α ) − t z sin ⁡ α 0 1 0 0 − sin ⁡ α 0 cos ⁡ α t z ( 1 − cos ⁡ α ) + t x sin ⁡ α 0 0 0 1 ] R α , z , ( t x , t y , 0 ) = [ cos ⁡ α − sin ⁡ α 0 t x ( 1 − cos ⁡ α ) − t z sin ⁡ α sin ⁡ α cos ⁡ α 0 t y ( 1 − cos ⁡ α ) − t x sin ⁡ α 0 0 1 0 0 0 0 1 ] \begin{aligned} \mathbf{R}{\alpha,x,(0,t_y,t_z)} &= \begin{bmatrix}1&0&0&0\\0&\cos\alpha&-\sin\alpha&t_y(1-\cos\alpha)+t_z\sin\alpha\\0&\sin\alpha&\cos\alpha&t_z(1-\cos\alpha)-t_y\sin\alpha\\0&0&0&1 \end{bmatrix} \\ \mathbf{R}{\alpha,y,(t_x,0,t_z)} &= \begin{bmatrix}\cos\alpha&0&\sin\alpha&t_x(1-\cos\alpha)-t_z\sin\alpha\\0&1&0&0\\-\sin\alpha&0&\cos\alpha&t_z(1-\cos\alpha)+t_x\sin\alpha\\0&0&0&1 \end{bmatrix} \\ \mathbf{R}_{\alpha,z,(t_x,t_y,0)} &= \begin{bmatrix}\cos\alpha&-\sin\alpha&0&t_x(1-\cos\alpha)-t_z\sin\alpha\\\sin\alpha&\cos\alpha&0&t_y(1-\cos\alpha)-t_x\sin\alpha\\0&0&1&0\\0&0&0&1 \end{bmatrix} \end{aligned} Rα,x,(0,ty,tz)Rα,y,(tx,0,tz)Rα,z,(tx,ty,0)= 10000cosαsinα00−sinαcosα00ty(1−cosα)+tzsinαtz(1−cosα)−tysinα1 = cosα0−sinα00100sinα0cosα0tx(1−cosα)−tzsinα0tz(1−cosα)+txsinα1 = cosαsinα00−sinαcosα000010tx(1−cosα)−tzsinαty(1−cosα)−txsinα01

4. 欧拉（Leonhard Euler）旋转：

   • 三种旋转方式：1）绕三个笛卡尔轴之一旋转；2）组合了围绕不同轴的任何两个旋转；3）组合了任何三个旋转。

   • 三个问题：1）当两个或更多旋转组合在一起时，很难可视化和预测最终旋转的行为；2）绕特定轴的旋转很复杂；3）万向节锁定（gimbal lock）：在某些条件下，对象的某个旋转轴无法被访问。

   • 十二种复合旋转
     R γ , x R β , y R α , x R γ , x R β , y R α , z R γ , x R β , z R α , x R γ , x R β , z R α , y R γ , y R β , x R α , y R γ , y R β , x R α , z R γ , y R β , z R α , x R γ , y R β , z R α , y R γ , z R β , x R α , y R γ , z R β , x R α , z R γ , z R β , y R α , x R γ , z R β , y R α , z \begin{matrix} {\mathbf{R}}{\gamma ,x}{\mathbf{R}}{\beta ,y}{\mathbf{R}}{\alpha ,x}&{\mathbf{R}}{\gamma ,x}{\mathbf{R}}{\beta ,y}{\mathbf{R}}{\alpha ,z}&{\mathbf{R}}{\gamma ,x}{\mathbf{R}}{\beta ,z}{\mathbf{R}}{\alpha ,x}&{\mathbf{R}}{\gamma ,x}\mathbf{R}{\beta,z}\mathbf{R}{\alpha,y} \\ {\mathbf{R}}{\gamma ,y}{\mathbf{R}}{\beta ,x}{\mathbf{R}}{\alpha ,y}&{\mathbf{R}}{\gamma ,y}{\mathbf{R}}{\beta ,x}{\mathbf{R}}{\alpha ,z}&{\mathbf{R}}{\gamma ,y}{\mathbf{R}}{\beta ,z}{\mathbf{R}}{\alpha ,x}&{\mathbf{R}}{\gamma ,y}\mathbf{R}{\beta,z}\mathbf{R}{\alpha,y} \\ {\mathbf{R}}{\gamma ,z}{\mathbf{R}}{\beta ,x}{\mathbf{R}}{\alpha ,y}&{\mathbf{R}}{\gamma ,z}{\mathbf{R}}{\beta ,x}{\mathbf{R}}{\alpha ,z}&{\mathbf{R}}{\gamma ,z}{\mathbf{R}}{\beta ,y}{\mathbf{R}}{\alpha ,x}& \mathbf{R}{\gamma,z}\mathbf{R}{\beta,y}\mathbf{R}{\alpha,z} \end{matrix} Rγ,xRβ,yRα,xRγ,yRβ,xRα,yRγ,zRβ,xRα,yRγ,xRβ,yRα,zRγ,yRβ,xRα,zRγ,zRβ,xRα,zRγ,xRβ,zRα,xRγ,yRβ,zRα,xRγ,zRβ,yRα,xRγ,xRβ,zRα,yRγ,yRβ,zRα,yRγ,zRβ,yRα,z

5. 绕任意轴旋转的矩阵

   • 旋转过程简述：将一个点 P P P绕单位向量 n ^ \hat{\boldsymbol{n}} n^旋转角 α \alpha α到点 P ′ P' P′

     • 示意图
       

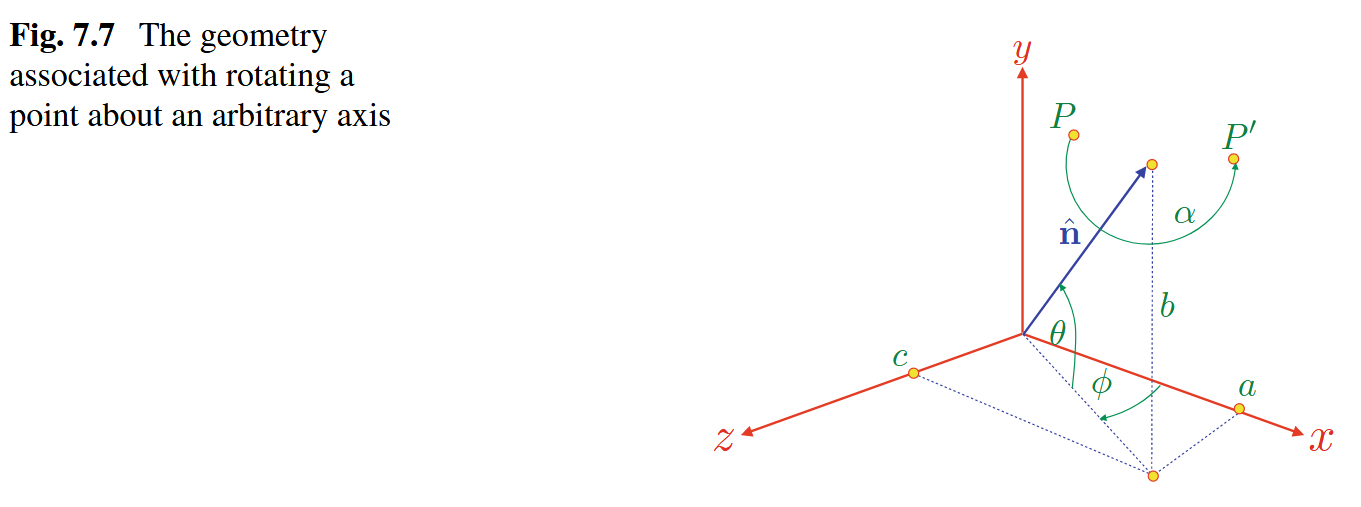
     • 在对齐过程中，点 P P P经历将单位载体与 X X X轴对齐所需的变换。然后我们绕 X X X轴旋转 P P P角 α \alpha α。为了完成该操作，旋转后的点将经历变换，让单位向量返回到其原始位置。

     • 此过程可以用矩阵形式描述为

       x ′ y ′ z ′ \] = R − ϕ , y R θ , z R α , x R θ , z R ϕ , y \[ x y z \] \\begin{bmatrix}x'\\\\y'\\\\z' \\end{bmatrix} = \\mathbf{R}_{-\\phi,y}\\mathbf{R}_{\\theta,z}\\mathbf{R}_{\\alpha,x}\\mathbf{R}_{\\theta,z}\\mathbf{R}_{\\phi,y}\\begin{bmatrix}x\\\\y\\\\z \\end{bmatrix} x′y′z′ =R−ϕ,yRθ,zRα,xRθ,zRϕ,y xyz

     R α , n ^ = [ a 2 K + cos ⁡ α a b K − c sin ⁡ α a c K + b sin ⁡ α a b K + c sin ⁡ α b 2 K + cos ⁡ α b c K − a sin ⁡ α a c K − b sin ⁡ α b c K + a sin ⁡ α c 2 K + cos ⁡ α ] K = 1 − cos ⁡ α n ^ = a i + b j + c k \begin{aligned} \mathbf{R}_{\alpha,\hat{\boldsymbol{n}}} &= \begin{bmatrix}a^2K+\cos\alpha&abK-c\sin\alpha&acK+b\sin\alpha\\abK+c\sin\alpha&b^2K+\cos\alpha&bcK-a\sin\alpha\\acK-b\sin\alpha&bcK+a\sin\alpha&c^2K+\cos\alpha \end{bmatrix} \\ K &= 1-\cos\alpha \\ \hat{\boldsymbol{n}} &= a\boldsymbol{i}+b\boldsymbol{j}+c\boldsymbol{k} \end{aligned} Rα,n^Kn^= a2K+cosαabK+csinαacK−bsinαabK−csinαb2K+cosαbcK+asinαacK+bsinαbcK−asinαc2K+cosα =1−cosα=ai+bj+ck

6. 罗德里格斯（Rodrigues）旋转公式

   • 欧拉-罗德里格斯参数化（Euler-Rodrigues Parameterisation）：将绕不同轴的两次连续旋转与绕另一轴的第三次旋转等同，即
     R γ , n = R α , I R β , m \mathbf{R}{\gamma,\boldsymbol{n}} = \mathbf{R}{\alpha,\boldsymbol{I}}\mathbf{R}_{\beta,\boldsymbol{m}} Rγ,n=Rα,IRβ,m

     且有
     cos ⁡ ( γ 2 ) = cos ⁡ ( α 2 ) cos ⁡ ( β 2 ) − sin ⁡ ( α 2 ) sin ⁡ ( β 2 ) I ⋅ m sin ⁡ ( γ 2 ) n = sin ⁡ ( α 2 ) cos ⁡ ( β 2 ) I + cos ⁡ ( α 2 ) sin ⁡ ( β 2 ) m + sin ⁡ ( α 2 ) sin ⁡ ( β 2 ) I × m \begin{aligned} \cos(\frac{\gamma}{2}) &= \cos(\frac{\alpha}{2})\cos(\frac{\beta}{2}) - \sin(\frac{\alpha}{2})\sin(\frac{\beta}{2})\boldsymbol{I}\cdot\boldsymbol{m} \\ \sin(\frac{\gamma}{2})\boldsymbol{n} &= \sin(\frac{\alpha}{2})\cos(\frac{\beta}{2})\boldsymbol{I} + \cos(\frac{\alpha}{2})\sin(\frac{\beta}{2})\boldsymbol{m} + \sin(\frac{\alpha}{2})\sin(\frac{\beta}{2})\boldsymbol{I}\times\boldsymbol{m} \end{aligned} cos(2γ)sin(2γ)n=cos(2α)cos(2β)−sin(2α)sin(2β)I⋅m=sin(2α)cos(2β)I+cos(2α)sin(2β)m+sin(2α)sin(2β)I×m

   • 罗德里格斯公式与四元数具有几乎一样的形式。

   • 罗德里格斯公式如今的表达式
     p ′ = p cos ⁡ α + n ^ ( n ^ ⋅ p ) ( 1 − cos ⁡ α ) + ( n ^ × p ) sin ⁡ α \boldsymbol{p}' = \boldsymbol{p}\cos\alpha + \hat{\boldsymbol{n}}(\hat{\boldsymbol{n}}\cdot\boldsymbol{p})(1-\cos\alpha) + (\hat{\boldsymbol{n}}\times\boldsymbol{p})\sin\alpha p′=pcosα+n^(n^⋅p)(1−cosα)+(n^×p)sinα

     其中， n ^ \hat{\boldsymbol{n}} n^是定义了任意旋转轴的单位向量； p \boldsymbol{p} p是被旋转的向量； α \alpha α是旋转角； p ′ \boldsymbol{p}' p′是旋转后的向量。

   • 罗德里格斯公式的矩阵形式
     R = I + ( sin ⁡ α ) K + ( 1 − cos ⁡ α ) K 2 \mathbf{R} = \boldsymbol{I} + (\sin\alpha)\boldsymbol{K} + (1-\cos\alpha)\boldsymbol{K}^2 R=I+(sinα)K+(1−cosα)K2

     其中， I \boldsymbol{I} I是单位矩阵； K \boldsymbol{K} K是旋转轴 n ^ \hat{\boldsymbol{n}} n^的反对称矩阵， K = [ 0 − n z n y n z 0 − n x − n y n x 0 ] \boldsymbol{K}=\begin{bmatrix}0&-n_z&n_y\\n_z&0&-n_x\\-n_y&n_x&0\end{bmatrix} K= 0nz−ny−nz0nxny−nx0 。

8 空间中的四元数

1. 合成代数（Composition Algebras）

   • 定义 ：合成代数是一类特殊的代数结构，它们满足一个称为"合成性质"的条件。具体来说，合成代数是一个带有乘法运算的向量空间，其中乘法满足以下性质：对于任意两个元素 x x x和 y y y，存在一个范数函数 N N N，使得
     N ( x ⋅ y ) = N ( x ) ⋅ N ( y ) N(x\cdot y) = N(x)\cdot N(y) N(x⋅y)=N(x)⋅N(y)

     其中， ⋅ \cdot ⋅代表代数中的乘法运算。

   • 关键特性：

     • 范数保持性：合成代数的核心特性是乘法运算保持范数，即两个元素的乘积的范数等于它们范数的乘积。
     • 维度限制 ：合成代数只能在特定的维度上存在，即 1、2、4 和 8 维。这些分别对应于实数 R \mathbb{R} R、复数 C \mathbb{C} C、四元数 H \mathbb{H} H和八元数 O \mathbb{O} O。
     • 非结合性：随着维度的增加，合成代数的结合性逐渐减弱。例如，四元数是非交换的，而八元数是非结合的。

   • **赫维兹定理（Hurwitz's Theorem）**或 1、2、4、8定理：在实数域 R \mathbb{R} R上，仅存在四种满足范数保持性质的合成代数，其维度分别为 1、2、4 和 8。因此，Hamilton对三元数体系的探索是徒劳的。

2. 四元数的乘积

   • 两个一般四元数相乘
     q a = [ s a , v a ] , q b = [ s b , v b ] q a q b = [ s a s b − v a ⋅ v b , s a v a + s b v b + v a × v b ] q_a=\begin{bmatrix}s_a,&\boldsymbol{v}_a \end{bmatrix},~~~ q_b=\begin{bmatrix}s_b,&\boldsymbol{v}_b \end{bmatrix} \\ q_aq_b = \begin{bmatrix}s_as_b-\boldsymbol{v}_a\cdot\boldsymbol{v}_b,&s_a\boldsymbol{v}_a+s_b\boldsymbol{v}_b+\boldsymbol{v}_a\times\boldsymbol{v}_b \end{bmatrix} qa=[sa,va], qb=[sb,vb]qaqb=[sasb−va⋅vb,sava+sbvb+va×vb]

   • 用 q q q去旋转 p p p （ p ′ = q p p'=qp p′=qp）：一个单位规范四元数 q q q和一个纯四元数 p p p相乘
     q = [ s , λ v ^ ] , ∣ v ^ ∣ = 1 , s 2 + λ 2 = 1 p = [ 0 , p ] , p ∈ R 3 p ′ = q p = [ − λ v ^ ⋅ p , s p + λ v ^ × p ] q=\begin{bmatrix}s,&\lambda\hat{\boldsymbol{v}} \end{bmatrix},~~~|\hat{\boldsymbol{v}}|=1,~s^2+\lambda^2=1 \\ p=\begin{bmatrix}0,&\boldsymbol{p} \end{bmatrix},~~~\boldsymbol{p}\in\mathbb{R}^3\\ p'=qp=\begin{bmatrix}-\lambda\hat{\boldsymbol{v}}\cdot\boldsymbol{p},&s\boldsymbol{p}+\lambda\hat{\boldsymbol{v}}\times\boldsymbol{p} \end{bmatrix} q=[s,λv^], ∣v^∣=1, s2+λ2=1p=[0,p], p∈R3p′=qp=[−λv^⋅p,sp+λv^×p]

     结果是一个一般四元数。

   • 特殊条件下使 p \boldsymbol{p} p绕着与之垂直的 v ^ \hat{\boldsymbol{v}} v^旋转角 θ \theta θ （ p ′ = q p p'=qp p′=qp）：一个单位规范四元数 q q q和一个与之"垂直"（ v ^ ⋅ p = 0 \hat{\boldsymbol{v}}\cdot\boldsymbol{p}=0 v^⋅p=0）的纯四元数 p p p相乘
     q = [ s , λ v ^ ] , ∣ v ^ ∣ = 1 , s 2 + λ 2 = 1 p = [ 0 , p ] , v ^ ⋅ p = 0 p ′ = [ 0 , s p + λ v ^ × p ] q=\begin{bmatrix}s,&\lambda\hat{\boldsymbol{v}} \end{bmatrix},~~~|\hat{\boldsymbol{v}}|=1,~s^2+\lambda^2=1 \\ p=\begin{bmatrix}0,&\boldsymbol{p} \end{bmatrix},~~~\hat{\boldsymbol{v}}\cdot\boldsymbol{p}=0\\ p'=\begin{bmatrix}0,&s\boldsymbol{p}+\lambda\hat{\boldsymbol{v}}\times\boldsymbol{p} \end{bmatrix} q=[s,λv^], ∣v^∣=1, s2+λ2=1p=[0,p], v^⋅p=0p′=[0,sp+λv^×p]

     由于 v ^ \hat{\boldsymbol{v}} v^是一个单位向量，因此 ∣ p ∣ = ∣ v ^ × p ∣ |\boldsymbol{p}|=|\hat{\boldsymbol{v}}\times\boldsymbol{p}| ∣p∣=∣v^×p∣，这意味 p ′ p' p′对应的向量分量两个长度相等且垂直。因此，为了使 p \boldsymbol{p} p绕着 v ^ \hat{\boldsymbol{v}} v^旋转角 θ \theta θ，只需令 s = cos ⁡ θ s=\cos\theta s=cosθ和 λ = sin ⁡ θ \lambda=\sin\theta λ=sinθ，有
     p ′ = q p = [ 0 , p ′ ] = [ 0 , cos ⁡ θ p + sin ⁡ θ v ^ × p ] p'=qp=\begin{bmatrix}0,&\boldsymbol{p}' \end{bmatrix} = \begin{bmatrix}0,&\cos\theta\boldsymbol{p}+\sin\theta\hat{\boldsymbol{v}}\times\boldsymbol{p} \end{bmatrix} p′=qp=[0,p′]=[0,cosθp+sinθv^×p]

     结果是一个纯四元数。另外，其实有四种乘法方式，其物理意义分别为：

     • p ′ = q p p'=qp p′=qp：使 p \boldsymbol{p} p绕着与之垂直的 v ^ \hat{\boldsymbol{v}} v^旋转角 θ \theta θ；
     • p ′ = p q p'=pq p′=pq：使 p \boldsymbol{p} p绕着与之垂直的 v ^ \hat{\boldsymbol{v}} v^旋转角 − θ -\theta −θ；
     • p ′ = q − 1 p = q ∗ p p'=q^{-1}p=q^*p p′=q−1p=q∗p：使 p \boldsymbol{p} p绕着与之垂直的 v ^ \hat{\boldsymbol{v}} v^旋转角 − θ -\theta −θ；
     • p ′ = p q − 1 p'=pq^{-1} p′=pq−1：使 p \boldsymbol{p} p绕着与之垂直的 v ^ \hat{\boldsymbol{v}} v^旋转角 θ \theta θ。

   • 一般情况下使 p \boldsymbol{p} p绕着 v ^ \hat{\boldsymbol{v}} v^旋转角 θ \theta θ （ p ′ = q p q − 1 p'=qpq^{-1} p′=qpq−1）：使用三重乘积
     q = [ s , λ v ^ ] , q − 1 = [ s , − λ v ^ ] , s 2 + λ 2 = 1 p = [ 0 , p ] q p q − 1 = [ λ 2 ( v ^ × p ) ⋅ v ^ , λ 2 ( v ^ ⋅ p ) v ^ + s 2 p + 2 λ s v ^ × p − λ 2 ( v ^ × p ) × v ^ ] = [ 0 , λ 2 ( v ^ ⋅ p ) v ^ + ( s 2 − λ 2 ) p + 2 λ s v ^ × p ] \begin{aligned} q &= \begin{bmatrix}s,&\lambda\hat{\boldsymbol{v}} \end{bmatrix} , ~q^{-1}=\begin{bmatrix}s,-\lambda\hat{\boldsymbol{v}} \end{bmatrix} ,~~~s^2+\lambda^2=1 \\ p &= \begin{bmatrix}0,&\boldsymbol{p} \end{bmatrix} \\ qpq^{-1} &= \begin{bmatrix}\lambda^2(\hat{\boldsymbol{v}}\times\boldsymbol{p})\cdot\hat{\boldsymbol{v}},&\lambda^2(\hat{\boldsymbol{v}}\cdot\boldsymbol{p})\hat{\boldsymbol{v}}+s^2\boldsymbol{p}+2\lambda s\hat{\boldsymbol{v}}\times\boldsymbol{p}-\lambda^2(\hat{\boldsymbol{v}}\times\boldsymbol{p})\times\hat{\boldsymbol{v}} \end{bmatrix}\\ &= \begin{bmatrix}0,&\lambda^2(\hat{\boldsymbol{v}}\cdot\boldsymbol{p})\hat{\boldsymbol{v}}+(s^2-\lambda^2)\boldsymbol{p}+2\lambda s\hat{\boldsymbol{v}}\times\boldsymbol{p} \end{bmatrix} \end{aligned} qpqpq−1=[s,λv^], q−1=[s,−λv^], s2+λ2=1=[0,p]=[λ2(v^×p)⋅v^,λ2(v^⋅p)v^+s2p+2λsv^×p−λ2(v^×p)×v^]=[0,λ2(v^⋅p)v^+(s2−λ2)p+2λsv^×p]

     令 s = cos ⁡ 1 2 θ s=\cos\frac{1}{2}\theta s=cos21θ和 λ = sin ⁡ 1 2 θ \lambda=\sin\frac{1}{2}\theta λ=sin21θ，有
     q = [ cos ⁡ 1 2 θ , sin ⁡ 1 2 θ v ^ ] q p q − 1 = [ 0 , ( 1 − cos ⁡ θ ) ( v ^ ⋅ p ) v ^ + cos ⁡ θ p + sin ⁡ θ v ^ × p ] q=\begin{bmatrix}\cos\frac{1}{2}\theta,&\sin\frac{1}{2}\theta\hat{\boldsymbol{v}}\end{bmatrix} \\ qpq^{-1} = \begin{bmatrix}0,&(1-\cos\theta)(\hat{\boldsymbol{v}}\cdot\boldsymbol{p})\hat{\boldsymbol{v}} + \cos\theta\boldsymbol{p} + \sin\theta\hat{\boldsymbol{v}}\times\boldsymbol{p} \end{bmatrix} q=[cos21θ,sin21θv^]qpq−1=[0,(1−cosθ)(v^⋅p)v^+cosθp+sinθv^×p]

     这是一个纯四元数。另外

     • q p q − 1 = [ 0 , ( 1 − cos ⁡ θ ) ( v ^ ⋅ p ) v ^ + cos ⁡ θ p + sin ⁡ θ v ^ × p ] qpq^{-1} = \begin{bmatrix}0,&(1-\cos\theta)(\hat{\boldsymbol{v}}\cdot\boldsymbol{p})\hat{\boldsymbol{v}} + \cos\theta\boldsymbol{p} + \sin\theta\hat{\boldsymbol{v}}\times\boldsymbol{p} \end{bmatrix} qpq−1=[0,(1−cosθ)(v^⋅p)v^+cosθp+sinθv^×p]：使 p \boldsymbol{p} p绕着 v ^ \hat{\boldsymbol{v}} v^旋转角 θ \theta θ
     • q − 1 p q = [ 0 , ( 1 − cos ⁡ θ ) ( v ^ ⋅ p ) v ^ + cos ⁡ θ p − sin ⁡ θ v ^ × p ] q^{-1}pq=\begin{bmatrix}0,&(1-\cos\theta)(\hat{\boldsymbol{v}}\cdot\boldsymbol{p})\hat{\boldsymbol{v}}+\cos\theta\boldsymbol{p}-\sin\theta\hat{\boldsymbol{v}}\times\boldsymbol{p} \end{bmatrix} q−1pq=[0,(1−cosθ)(v^⋅p)v^+cosθp−sinθv^×p]：使 p \boldsymbol{p} p绕着 v ^ \hat{\boldsymbol{v}} v^旋转角 − θ -\theta −θ。

   • 总结：

     • 通过四元数旋转向量
       q = [ s v ] , s 2 + ∣ v ∣ 2 = 1 , p = [ 0 p ] q p q − 1 = [ 0 2 ( v ⋅ p ) v + ( 2 s 2 − 1 ) p + 2 s v × p ] q = [ cos ⁡ ( θ 2 ) sin ⁡ ( θ 2 ) v ^ ] , p = [ 0 p ] q p q − 1 = [ 0 ( 1 − cos ⁡ θ ) ( v ^ ⋅ p ) v ^ + cos ⁡ θ p + sin ⁡ θ v ^ × p ] \begin{aligned} q &= \begin{bmatrix}s &\boldsymbol{v} \end{bmatrix},~ s^2+|v|^2 = 1,~ p = \begin{bmatrix}0 &\boldsymbol{p} \end{bmatrix}\\ qpq^{-1} &= \begin{bmatrix}0 & 2(\boldsymbol{v}\cdot\boldsymbol{p})\boldsymbol{v}+(2s^2-1)\boldsymbol{p}+2s\boldsymbol{v}\times\boldsymbol{p} \end{bmatrix}\\ q &= \begin{bmatrix}\cos(\frac{\theta}{2})&\sin(\frac{\theta}{2})\hat{\boldsymbol{v}} \end{bmatrix},~ p = \begin{bmatrix}0&\boldsymbol{p} \end{bmatrix}\\ qpq^{-1} &= \begin{bmatrix}0&(1-\cos\theta)(\hat{\boldsymbol{v}}\cdot\boldsymbol{p})\hat{\boldsymbol{v}}+\cos\theta\boldsymbol{p}+\sin\theta\hat{\boldsymbol{v}}\times\boldsymbol{p} \end{bmatrix} \end{aligned} qqpq−1qqpq−1=[sv], s2+∣v∣2=1, p=[0p]=[02(v⋅p)v+(2s2−1)p+2sv×p]=[cos(2θ)sin(2θ)v^], p=[0p]=[0(1−cosθ)(v^⋅p)v^+cosθp+sinθv^×p]

     • 通过四元数旋转坐标系 （当使用 q − 1 p q q^{-1}pq q−1pq时，虽然旋转方向相反，但它可以等效理解为改变参照系（坐标系）的旋转）
       q − 1 p q = [ 0 ( 1 − cos ⁡ θ ) ( v ^ ⋅ p ) v ^ + cos ⁡ θ p − sin ⁡ θ v ^ × p ] q^{-1}pq = \begin{bmatrix}0&(1-\cos\theta)(\hat{\boldsymbol{v}}\cdot\boldsymbol{p})\hat{\boldsymbol{v}}+\cos\theta\boldsymbol{p}-\sin\theta\hat{\boldsymbol{v}}\times\boldsymbol{p} \end{bmatrix} q−1pq=[0(1−cosθ)(v^⋅p)v^+cosθp−sinθv^×p]

       • 假设你面对北方，将一本书顺时针旋转 90 度（主动旋转），书的朝向变为东方。
       • 如果你保持书不动，但自己逆时针转 90 度（被动旋转），书的相对朝向也会变为东方。

3. 四元数的矩阵表示

   • 方法一：使用向量方法获得矩阵表示

     • 通过上一节获得表达式： p ′ = [ 0 , p ′ ] = q p q − 1 = ⋯ p'=\begin{bmatrix}0,&\boldsymbol{p}' \end{bmatrix}=qpq^{-1}=\cdots p′=[0,p′]=qpq−1=⋯或者 p ′ = [ 0 , p ′ ] = q − 1 p q = ⋯ p'=\begin{bmatrix}0,&\boldsymbol{p}' \end{bmatrix}=q^{-1}pq=\cdots p′=[0,p′]=q−1pq=⋯；

     • 因此有
       p ′ = 2 ( v ⋅ p ) v + ( 2 s 2 − 1 ) p + 2 s v × p or p ′ = 2 ( v ⋅ p ) v + ( 2 s 2 − 1 ) p − 2 s v × p \boldsymbol{p}' = 2(\boldsymbol{v}\cdot\boldsymbol{p})\boldsymbol{v}+(2s^2-1)\boldsymbol{p}+2s\boldsymbol{v}\times\boldsymbol{p} \\ \text{or } \boldsymbol{p}' = 2(\boldsymbol{v}\cdot\boldsymbol{p})\boldsymbol{v}+(2s^2-1)\boldsymbol{p}-2s\boldsymbol{v}\times\boldsymbol{p} p′=2(v⋅p)v+(2s2−1)p+2sv×por p′=2(v⋅p)v+(2s2−1)p−2sv×p

     • 代入
       v = x i + y j + z k = [ i j k ] [ x y z ] and p = x p i + y p j + z p k = [ i j k ] [ x p y p z p ] \boldsymbol{v} = x\boldsymbol{i}+y\boldsymbol{j}+\boldsymbol{z}k = \begin{bmatrix}\boldsymbol{i}&\boldsymbol{j}&\boldsymbol{k} \end{bmatrix}\begin{bmatrix}x\\y\\z \end{bmatrix}\\ \text{and } \boldsymbol{p} = x_p\boldsymbol{i} + y_p\boldsymbol{j} + z_p\boldsymbol{k} = \begin{bmatrix}\boldsymbol{i}&\boldsymbol{j}&\boldsymbol{k} \end{bmatrix}\begin{bmatrix}x_p\\y_p\\z_p \end{bmatrix} v=xi+yj+zk=[ijk] xyz and p=xpi+ypj+zpk=[ijk] xpypzp

     • 根据右端向量不同（ [ x , y , z ] T [x,y,z]^T [x,y,z]T或者 [ x p , y p , z p ] T [x_p,y_p,z_p]^T [xp,yp,zp]T），化简后得到两种矩阵表达式。

   • 方法二：使用矩阵方法获得矩阵表示

     • 由四元数乘法矩阵形式，根据右端向量不同可以有两种表示
       q a q b = L ( q a ) q b = [ s 1 − x 1 − y 1 − z 1 x 1 s 1 − z 1 y 1 y 1 z 1 s 1 − x 1 z 1 − y 1 x 1 s 1 ] [ s 2 x 2 y 2 z 2 ] = R ( q b ) q a = [ s 2 − x 2 − y 2 − z 2 x 2 s 2 z 2 − y 2 y 2 − z 2 s 2 x 2 z 2 y 2 − x 2 s 2 ] [ s 1 x 1 y 1 z 1 ] \begin{aligned} q_aq_b &= \boldsymbol{L}(q_a)q_b = \begin{bmatrix} s_1 &-x_1 &-y_1 &-z_1\\ x_1 &s_1 &-z_1 &y_1\\ y_1 &z_1 &s_1 &-x_1\\ z_1 &-y_1 &x_1 &s_1 \end{bmatrix}\begin{bmatrix} s_2\\x_2\\y_2\\z_2 \end{bmatrix} \\ &= \boldsymbol{R}(q_b)q_a = \begin{bmatrix} s_2 &-x_2 &-y_2 &-z_2\\ x_2 &s_2 &z_2 &-y_2\\ y_2 &-z_2 &s_2 &x_2\\ z_2 &y_2 &-x_2 &s_2 \end{bmatrix}\begin{bmatrix} s_1\\x_1\\y_1\\z_1 \end{bmatrix} \end{aligned} qaqb=L(qa)qb= s1x1y1z1−x1s1z1−y1−y1−z1s1x1−z1y1−x1s1 s2x2y2z2 =R(qb)qa= s2x2y2z2−x2s2−z2y2−y2z2s2−x2−z2−y2x2s2 s1x1y1z1

     • 计算 q p q − 1 qpq^{-1} qpq−1和 q − 1 p q q^{-1}pq q−1pq
       q p q − 1 = ( q p ) q − 1 = ( L ( q ) p ) q − 1 = R ( q − 1 ) ( L ( q ) p ) = ( R ( q − 1 ) L ( q ) ) p q − 1 p q = ( q − 1 p ) q = ( L ( q − 1 ) p ) q = R ( q ) ( L ( q − 1 ) p ) = ( R ( q ) L ( q − 1 ) ) p \begin{aligned} qpq^{-1} = (qp)q^{-1} = (\boldsymbol{L}(q)p)q^{-1} = \boldsymbol{R}(q^{-1})(\boldsymbol{L}(q)p)=(\boldsymbol{R}(q^{-1})\boldsymbol{L}(q))p\\ q^{-1}pq = (q^{-1}p)q = (\boldsymbol{L}(q^{-1})p)q = \boldsymbol{R}(q)(\boldsymbol{L}(q^{-1})p)=(\boldsymbol{R}(q)\boldsymbol{L}(q^{-1}))p \end{aligned} qpq−1=(qp)q−1=(L(q)p)q−1=R(q−1)(L(q)p)=(R(q−1)L(q))pq−1pq=(q−1p)q=(L(q−1)p)q=R(q)(L(q−1)p)=(R(q)L(q−1))p

     • 然后计算 ( R ( q − 1 ) L ( q ) ) (\boldsymbol{R}(q^{-1})\boldsymbol{L}(q)) (R(q−1)L(q))和 ( R ( q ) L ( q − 1 ) ) (\boldsymbol{R}(q)\boldsymbol{L}(q^{-1})) (R(q)L(q−1))，并删去第一行和第一列，就得到了矩阵表达式。

   • 总结：

     • 通过四元数旋转向量时的矩阵
       p ′ = q p q − 1 = [ 1 − 2 ( y 2 + z 2 ) 2 ( x y − s z ) 2 ( x z + s y ) 2 ( x y + s z ) 1 − 2 ( x 2 + z 2 ) 2 ( y z − s x ) 2 ( x z − s y ) 2 ( y z + s x ) 1 − 2 ( x 2 + y 2 ) ] [ x p y p z p ] \boldsymbol{p}' =qpq^{-1} = \begin{bmatrix}1-2(y^2+z^2)&2(xy-sz)&2(xz+sy)\\2(xy+sz)&1-2(x^2+z^2)&2(yz-sx)\\2(xz-sy)&2(yz+sx)&1-2(x^2+y^2) \end{bmatrix}\begin{bmatrix} x_p\\y_p\\z_p \end{bmatrix} p′=qpq−1= 1−2(y2+z2)2(xy+sz)2(xz−sy)2(xy−sz)1−2(x2+z2)2(yz+sx)2(xz+sy)2(yz−sx)1−2(x2+y2) xpypzp

     • 通过四元数旋转坐标系时的矩阵
       p ′ = q − 1 q p = [ 1 − 2 ( y 2 + z 2 ) 2 ( x y + s z ) 2 ( x y − s y ) 2 ( x y − s z ) 1 − 2 ( x 2 + z 2 ) 2 ( y z + s x ) 2 ( x z + s y ) 2 ( y z − s x ) 1 − 2 ( x 2 + y 2 ) ] [ x p y p z p ] \boldsymbol{p}' = q^{-1}qp = \begin{bmatrix}1-2(y^2+z^2)&2(xy+sz)&2(xy-sy)\\2(xy-sz)&1-2(x^2+z^2)&2(yz+sx)\\2(xz+sy)&2(yz-sx)&1-2(x^2+y^2) \end{bmatrix}\begin{bmatrix} x_p\\y_p\\z_p \end{bmatrix} p′=q−1qp= 1−2(y2+z2)2(xy−sz)2(xz+sy)2(xy+sz)1−2(x2+z2)2(yz−sx)2(xy−sy)2(yz+sx)1−2(x2+y2) xpypzp

4. 多个旋转

   • 假设一个向量或参考系受到 q 1 q_1 q1和 q 2 q_2 q2指定的两次旋转，最好的方法是将旋转累计为四元数，然后再转换为矩阵符号。

   • 考虑纯四元数 p p p受到第一个四元数 q 1 q_1 q1的影响： q q p q 1 − 1 q_qpq_1^{-1} qqpq1−1；

     后面跟着第二个四元数 q 2 q_2 q2： q 2 ( q q p q 1 − 1 ) q 2 − 1 q_2(q_qpq_1^{-1})q_2^{-1} q2(qqpq1−1)q2−1；

     这可以表示为：
     ( q 2 q 1 ) p ( q 2 q 1 ) − 1 (q_2q_1)p(q_2q_1)^{-1} (q2q1)p(q2q1)−1

5. 绕偏移轴旋转

   • 在第6章中，使用了下面的记号

     x ′ y ′ z ′ 1 \] = T t x , 0 , t z R β , y T − t x , 0 , − t z \[ x y z 1 \] \\begin{bmatrix} x'\\\\y'\\\\z'\\\\1\\end{bmatrix} = \\mathbf{T}_{t_x,0,t_z}\\mathbf{R}_{\\beta,y}\\mathbf{T}_{-t_x,0,-t_z}\\begin{bmatrix} x\\\\y\\\\z\\\\1 \\end{bmatrix} x′y′z′1 =Ttx,0,tzRβ,yT−tx,0,−tz xyz1 来绕与y轴平行的固定轴旋转一点。

     x ′ y ′ z ′ 1 \] = T t x , 0 , t z ( q p q − 1 ) T − t x , 0 , − t z \[ x y z 1 \] \\begin{bmatrix}x'\\\\y'\\\\z'\\\\1 \\end{bmatrix} = \\mathbf{T}_{t_x,0,t_z}(qpq\^{-1})\\mathbf{T}_{-t_x,0,-t_z}\\begin{bmatrix} x\\\\y\\\\z\\\\1 \\end{bmatrix} x′y′z′1 =Ttx,0,tz(qpq−1)T−tx,0,−tz xyz1

   • Slerp球面线性插值方法 ：给定两个四元数 q 1 q_1 q1和 q 2 q_2 q2，Slerp公式为
     q = sin ⁡ [ ( 1 − t ) θ ] sin ⁡ θ q 1 + sin ⁡ ( t θ ) sin ⁡ θ q 2 q = \frac{\sin[(1-t)\theta]}{\sin\theta}q_1 + \frac{\sin(t\theta)}{\sin\theta}q_2 q=sinθsin[(1−t)θ]q1+sinθsin(tθ)q2

     其中， t ∈ [ 0 , 1 ] t\in[0,1] t∈[0,1]为插值的权重系数，且
     cos ⁡ θ = q 1 ⋅ q 2 ∣ q 1 ∣ ∣ q 2 ∣ = s 1 s 2 + x 1 x 2 + y 1 y 2 + z 1 z 2 ∣ q 1 ∣ ∣ q 2 ∣ \cos\theta = \frac{q_1\cdot q_2}{|q_1||q_2|} = \frac{s_1s_2+x_1x_2+y_1y_2+z_1z_2}{|q_1||q_2|} cosθ=∣q1∣∣q2∣q1⋅q2=∣q1∣∣q2∣s1s2+x1x2+y1y2+z1z2

     表示在四维单位球面上，沿着连接 q 1 q_1 q1和 q 2 q_2 q2的最短路径（即大圆弧）进行插值。

   • 几何意义：四元数位于四维单位球面，Slerp 通过正弦函数权重分配，确保插值路径始终在球面上，从而保持旋转的最短弧长和恒定角速度。

6. 将旋转矩阵转换为四元数

   • q p q − 1 qpq^{-1} qpq−1的等价矩阵变换为
     q p q − 1 = [ 1 − 2 ( y 2 + z 2 ) 2 ( x y − s z ) 2 ( x z + s y ) 2 ( x y + s z ) 1 − 2 ( x 2 + z 2 ) 2 ( y z − s x ) 2 ( x z − s y ) 2 ( y z + s x ) 1 − 2 ( x 2 + y 2 ) ] [ x p y p z p ] = [ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ] [ x p y p z p ] \begin{aligned} qpq^{-1} &= \begin{bmatrix}1-2(y^2+z^2)&2(xy-sz)&2(xz+sy)\\2(xy+sz)&1-2(x^2+z^2)&2(yz-sx)\\2(xz-sy)&2(yz+sx)&1-2(x^2+y^2) \end{bmatrix}\begin{bmatrix} x_p\\y_p\\z_p \end{bmatrix} \\&=\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33} \end{bmatrix}\begin{bmatrix} x_p\\y_p\\z_p \end{bmatrix} \end{aligned} qpq−1= 1−2(y2+z2)2(xy+sz)2(xz−sy)2(xy−sz)1−2(x2+z2)2(yz+sx)2(xz+sy)2(yz−sx)1−2(x2+y2) xpypzp = a11a21a31a12a22a32a13a23a33 xpypzp

     通过组合各种元素，可以分离出四元数 s , x , y , z s,x,y,z s,x,y,z的值。

   • 结果一
     s = 1 2 1 + a 11 + a 22 + a 33 x = 1 4 s ( a 32 − a 23 ) y = 1 4 s ( a 13 − a 31 ) z = 1 4 s ( a 21 − a 12 ) \begin{aligned} s&=\frac{1}{2}\sqrt{1+a_{11}+a_{22}+a_{33}}\\ x&=\frac{1}{4s}(a_{32}-a_{23})\\ y&=\frac{1}{4s}(a_{13}-a_{31})\\ z&=\frac{1}{4s}(a_{21}-a_{12}) \end{aligned} sxyz=211+a11+a22+a33 =4s1(a32−a23)=4s1(a13−a31)=4s1(a21−a12)

   • 结果二
     x = 1 2 1 + a 11 − a 22 − a 33 y = 1 4 x ( a 12 + a 21 ) z = 1 4 x ( a 13 + a 31 ) s = 1 4 x ( a 32 − a 23 ) \begin{aligned} x&=\frac{1}{2}\sqrt{1+a_{11}-a_{22}-a_{33}}\\ y&=\frac{1}{4x}(a_{12}+a_{21})\\ z&=\frac{1}{4x}(a_{13}+a_{31})\\ s&=\frac{1}{4x}(a_{32}-a_{23}) \end{aligned} xyzs=211+a11−a22−a33 =4x1(a12+a21)=4x1(a13+a31)=4x1(a32−a23)

   • 结果三
     y = 1 2 1 − a 11 + a 22 − a 33 x = 1 4 y ( a 12 + q 21 ) z = 1 4 y ( a 23 + a 32 ) s = 1 4 y ( a 13 − a 31 ) \begin{aligned} y&=\frac{1}{2}\sqrt{1-a_{11}+a_{22}-a_{33}}\\ x&=\frac{1}{4y}(a_{12}+q_{21})\\ z&=\frac{1}{4y}(a_{23}+a_{32})\\ s&=\frac{1}{4y}(a_{13}-a_{31}) \end{aligned} yxzs=211−a11+a22−a33 =4y1(a12+q21)=4y1(a23+a32)=4y1(a13−a31)

   • 结果四
     z = 1 2 1 − a 11 − a 22 + a 33 x = 1 4 z ( a 13 + a 31 ) y = 1 4 z ( a 23 + a 32 ) s = 1 4 z ( a 21 − a 12 ) \begin{aligned} z&=\frac{1}{2}\sqrt{1-a_{11}-a_{22}+a_{33}}\\ x&=\frac{1}{4z}(a_{13}+a_{31})\\ y&=\frac{1}{4z}(a_{23}+a_{32})\\ s&=\frac{1}{4z}(a_{21}-a_{12}) \end{aligned} zxys=211−a11−a22+a33 =4z1(a13+a31)=4z1(a23+a32)=4z1(a21−a12)

7. 欧拉角转换到四元数

   • 基于变换 R γ , z R β , y R α , x \boldsymbol{R}{\gamma,z}\boldsymbol{R}{\beta,y}\boldsymbol{R}_{\alpha,x} Rγ,zRβ,yRα,x
     s = cos ⁡ ( γ 2 ) cos ⁡ ( β 2 ) cos ⁡ ( α 2 ) + sin ⁡ ( γ 2 ) sin ⁡ ( β 2 ) sin ⁡ ( α 2 ) x q = cos ⁡ ( γ 2 ) cos ⁡ ( β 2 ) sin ⁡ ( α 2 ) − sin ⁡ ( γ 2 ) sin ⁡ ( β 2 ) cos ⁡ ( α 2 ) y q = cos ⁡ ( γ 2 ) sin ⁡ ( β 2 ) cos ⁡ ( α 2 ) + sin ⁡ ( γ 2 ) cos ⁡ ( β 2 ) sin ⁡ ( α 2 ) z q = sin ⁡ ( γ 2 ) cos ⁡ ( β 2 ) cos ⁡ ( α 2 ) − cos ⁡ ( γ 2 ) sin ⁡ ( β 2 ) sin ⁡ ( α 2 ) \begin{aligned} s &= \cos(\frac{\gamma}{2})\cos(\frac{\beta}{2})\cos(\frac{\alpha}{2}) + \sin(\frac{\gamma}{2})\sin(\frac{\beta}{2})\sin(\frac{\alpha}{2}) \\ x_q &= \cos(\frac{\gamma}{2})\cos(\frac{\beta}{2})\sin(\frac{\alpha}{2}) - \sin(\frac{\gamma}{2})\sin(\frac{\beta}{2})\cos(\frac{\alpha}{2}) \\ y_q &= \cos(\frac{\gamma}{2})\sin(\frac{\beta}{2})\cos(\frac{\alpha}{2}) + \sin(\frac{\gamma}{2})\cos(\frac{\beta}{2})\sin(\frac{\alpha}{2}) \\ z_q &= \sin(\frac{\gamma}{2})\cos(\frac{\beta}{2})\cos(\frac{\alpha}{2}) - \cos(\frac{\gamma}{2})\sin(\frac{\beta}{2})\sin(\frac{\alpha}{2}) \end{aligned} sxqyqzq=cos(2γ)cos(2β)cos(2α)+sin(2γ)sin(2β)sin(2α)=cos(2γ)cos(2β)sin(2α)−sin(2γ)sin(2β)cos(2α)=cos(2γ)sin(2β)cos(2α)+sin(2γ)cos(2β)sin(2α)=sin(2γ)cos(2β)cos(2α)−cos(2γ)sin(2β)sin(2α)
     其中
     q = [ s x q i + y q j + z q k ] q=\begin{bmatrix}s&x_q\boldsymbol{i}+y_q\boldsymbol{j}+z_q\boldsymbol{k} \end{bmatrix} q=[sxqi+yqj+zqk]

8. 本章小结

   • 本章是本书的重点，其中单位规范四元数用于围绕 一个四元数的向量 旋转一个 向量。如果这能像复数一样，由简单积 q p qp qp来实现，那就很有用了。但正如我们看到的，这只适用于四元数与向量正交的情况。由Hamilton和Cayley发现的积 q p q − 1 qpq^{-1} qpq−1，适用于四元数和向量之间的所有方向，它也相对容易计算。我们还看到乘积可以表示为一个矩阵，这个矩阵可以与其它矩阵相乘。
   • 也许本章中出现的四元数最有趣的特征之一，是它们的虚数性质在任何计算中都不需要，因为它们嵌入在代数中。
   • 球面插补提供了一种动态改变四元数轴和旋转角度的聪明方法，但如果没有实时显示系统，则很难将其可视化为动画序列。
   • 反向乘积 q − 1 p q q^{-1}pq q−1pq反转了旋转角度，等价于改变 q p q − 1 qpq^{-1} qpq−1中旋转角度的符号。因此，它可以用来旋转一个参考系，旋转方向与 q p q − 1 qpq^{-1} qpq−1相同。