昆明天气数据分析与挖掘（四）- 昆明气温数据预测分析

大数据魔法师2026-02-14 8:29

昆明气温数据预测分析

  • 一、气温预测目标
  • 二、特征工程
    • [1. 预测特征及目标数据准备](#1. 预测特征及目标数据准备)
    • [2. 季节特征编码](#2. 季节特征编码)
    • [3. 数据集划分](#3. 数据集划分)
  • 三、模型构建
    • [1. 模型选择](#1. 模型选择)
    • [2. 确定模型最优参数组合](#2. 确定模型最优参数组合)
    • [3. 模型训练与预测](#3. 模型训练与预测)
  • 四、模型评估
    • [1. 预测结果可视化](#1. 预测结果可视化)
      • [1.1 真实值与预测值数据可视化](#1.1 真实值与预测值数据可视化)
      • [1.2 误差分布数据可视化](#1.2 误差分布数据可视化)
    • [2. 核心评估指标](#2. 核心评估指标)
    • [3. 特征重要性数据可视化分析](#3. 特征重要性数据可视化分析)
      • [3.1 特征重要性数据分析](#3.1 特征重要性数据分析)
      • [3.2 特征重要性数据可视化](#3.2 特征重要性数据可视化)
  • 五、完整代码

一、气温预测目标

本研究以随机森林回归模型为核心，选取年份、月份、日期、星期数、季节、年内天数等日期衍生属性作为输入特征，实现对昆明市单日最高气温与最低气温的定量回归预测，预测结果以摄氏度（℃）为单位输出，旨在为昆明市短期气温趋势研判提供量化参考。

二、特征工程

1. 预测特征及目标数据准备

数据准备的核心目的是从预处理后的数据集里筛选出适配气温预测任务的特征变量与目标变量，构建模型训练所需的输入特征矩阵与输出目标向量，为后续模型训练提供标准化的数据基础。

本研究结合气温预测的需求，选取年份、月份、日期、星期数、星期、年内天数、季节共 7 个日期衍生属性作为预测特征；同时将最低气温（min_temperature）、最高气温（max_temperature）分别作为两个预测任务的目标变量。具体过程为如下代码所示，首先加载预处理后的昆明天气数据集，再从数据集中提取上述 7 个特征字段组成特征矩阵，分别提取最低气温、最高气温字段作为对应预测任务的目标向量。

python 复制代码 
# 1. 数据准备
# 加载数据
raw_data_path = '../数据预处理/data/昆明天气数据_清洗后.csv'
df = pd.read_csv(raw_data_path, encoding='utf-8-sig')
# 数据准备
FEATURES = ['year', 'month', 'day', 'week', 'weekday', 'dayofyear', 'season']
X = df[FEATURES]
y_min = df['min_temperature']
print(f"\n最低气温建模数据准备完成:")
print(f"特征矩阵X形状: {X.shape}，目标变量y形状: {y_min.shape}")
y_max = df['max_temperature']
print(f"\n最高气温建模数据准备完成:")
print(f"特征矩阵X形状: {X.shape}，目标变量y形状: {y_max.shape}")

数据准备完成后的运行结果如下图所示，最低气温建模任务的特征矩阵形状为 (5469, 7)，对应 5469 条样本、7 个特征；目标变量形状为 (5469,)，对应 5469 条样本的最低气温值。最高气温建模任务的特征矩阵与目标变量形状与最低气温任务一致，说明两个预测任务的样本量、特征维度均匹配，数据准备结果符合模型训练的输入要求。

2. 季节特征编码

在当前数据中，"季节"字段是以"春季""夏季"等文本类别形式存储，这类文本型特征无法直接输入到随机森林回归模型中参与计算，是数据适配模型训练的核心问题。季节特征编码的目的是将文本型的季节类别转换为模型可识别的数值型特征，消除文本格式对模型输入的限制，同时保留季节特征的类别信息，保证其对气温预测的贡献价值。

具体处理过程如下代码所示，针对 "季节" 字段的文本类别，构建对应映射规则，将 "春季""夏季""秋季""冬季" 分别转换为对应的数值标识，再基于该规则对数据集中的 "季节" 字段进行批量转换。

python 复制代码 
# 2. 季节特征编码
SEASON_MAPPING = {'春季': 0, '夏季': 1, '秋季': 2, '冬季': 3}
df['season'] = df['season'].map(SEASON_MAPPING)
X = df[FEATURES]

编码前后结果如下图所示，编码前以 "冬季" 为文本形式的季节特征，编码后统一转换为对应的数值标识，文本型特征成功转化为数值型特征。这一处理结果既保留了季节的类别区分信息，又满足了模型对数值型输入特征的要求，为后续模型训练提供了合规的特征数据。

3. 数据集划分

数据集划分的核心目的是将已预处理的特征与目标数据拆分为训练集与测试集：训练集用于模型的参数学习与拟合，测试集用于验证模型在新数据上的泛化能力，以此客观评估模型的预测性能。

具体划分过程如下代码所示，针对最低气温、最高气温两个预测任务，分别将对应的特征矩阵与目标向量按7:3比例拆分，同时对数据进行随机打乱，避免样本顺序对模型训练的干扰，保证划分结果的随机性与代表性。

python 复制代码 
# 3. 数据集划分
X_train_min, X_test_min, y_train_min, y_test_min = train_test_split(
    X, y_min, test_size=0.3, random_state=42, shuffle=True
)
print(f"最低气温训练集特征形状: {X_train_min.shape}，目标形状: {y_train_min.shape}")
print(f"最低气温测试集特征形状: {X_test_min.shape}，目标形状: {y_test_min.shape}")
print(f"最低气温训练集占比: {len(X_train_min) / len(y_min) * 100:.1f}%")
print(f"最低气温测试集占比: {len(X_test_min) / len(y_min) * 100:.1f}%")
X_train_max, X_test_max, y_train_max, y_test_max = train_test_split(
    X, y_max, test_size=0.3, random_state=42, shuffle=True
)
print(f"最高气温训练集特征形状: {X_train_max.shape}，目标形状: {y_train_max.shape}")
print(f"最高气温测试集特征形状: {X_test_max.shape}，目标形状: {y_test_max.shape}")
print(f"最高气温训练集占比: {len(X_train_max) / len(y_max) * 100:.1f}%")
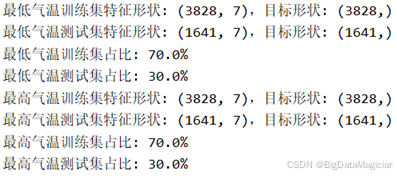
print(f"最高气温测试集占比: {len(X_test_max) / len(y_max) * 100:.1f}%")

数据集划分结果如下图所示，最低气温预测任务中，训练集特征矩阵有3828条样本与7个特征，目标向量有382条样本；测试集特征矩阵有1641条样本与7个特征，目标向量有1641条样本，训练集占比 70.0%，测试集占比 30.0%。最高气温预测任务的划分结果与最低气温任务完全一致，说明两个任务的训练、测试数据规模与特征维度均匹配，划分结果符合模型训练与性能验证的需求，能够支撑后续的模型训练与效果评估。

三、模型构建

1. 模型选择

本研究选用随机森林回归模型，昆明市气温与日期特征间存在复杂的非线性关联，随机森林基于集成学习框架，可有效捕捉这种非线性映射关系，优于线性回归等模型；通过 "随机采样样本 + 随机选择特征" 的双重随机机制，模型抗过拟合能力突出，能降低气象数据随机干扰带来的误差，保证预测稳定性；该模型在scikit-learn库中实现成熟，参数调优逻辑清晰，无需复杂的底层代码编写。

2. 确定模型最优参数组合

确定模型最优参数组合的核心目的是通过系统性的参数寻优，提升随机森林回归模型对昆明市气温的预测精度与泛化能力，避免因参数设置不当导致模型过拟合或欠拟合，从而保证后续气温预测结果的可靠性。

具体实施过程如下代码所示，采用网格搜索结合5折交叉验证的方式开展参数寻优。首先针对随机森林回归模型的决策树数量、树最大深度、特征采样比例等核心参数设定合理的参数候选范围；随后将训练集划分为 5 个子集，依次以其中 4 个子集作为训练数据、1 个子集作为验证数据，遍历所有参数组合进行模型训练与验证；最后以交叉验证得到的均方误差（MSE）为评价指标，筛选出使模型性能最优的参数组合。

python 复制代码 
4. 网格搜索确定最优参数组合
min_best_params, min_best_neg_mse, min_best_rmse = grid_search_best_params(
    X_train_min, y_train_min)
print(f"\n最低气温最优参数组合: {min_best_params}")
print(f"最低气温最优交叉验证得分 (负MSE): {min_best_neg_mse:.4f}")
print(f"最低气温最优交叉验证得分 (RMSE): {min_best_rmse:.4f}")
max_best_params, max_best_neg_mse, max_best_rmse = grid_search_best_params(
    X_train_max, y_train_max)
print(f"\n最高气温最优参数组合: {max_best_params}")
print(f"最高气温最优交叉验证得分 (负MSE): {max_best_neg_mse:.4f}")
print(f"最高气温最优交叉验证得分 (RMSE): {max_best_rmse:.4f}")

寻优结果如下图所示，最低气温预测模型的最优参数组合为最大深度为20、特征数量比例为1.0、叶子节点最小样本数为1、节点可分裂的最小样本数为2、决策树的数量为300，该最优参数组合下的交叉验证均方误差（MSE）为 1.9960，对应均方根误差（RMSE）为 1.428，表明模型在验证集上的预测误差较小；最高气温预测模型的最优参数组合为最大深度为20、特征数量比例为1.0、叶子节点最小样本数为1、节点可分裂的最小样本数为2、决策树的数量为300；该参数寻优过程通过网格搜索的系统性遍历与交叉验证的稳定性验证，确保了参数组合的最优性，为后续构建高精度的气温预测模型奠定了坚实基础。

3. 模型训练与预测

模型训练与预测的核心目的是基于已确定的最优参数组合，构建昆明市最低气温与最高气温的预测模型，并通过测试集验证模型的实际预测性能，输出量化的预测结果，为气温趋势研判提供具体的数值参考。

模型训练与预测过程如下代码所示，针对最低气温与最高气温两个预测任务分别开展模型训练，首先将网格搜索得到的最优参数组合代入随机森林回归模型，以训练集的特征矩阵与目标向量为输入完成模型拟合；随后将测试集的特征矩阵输入已训练完成的模型，生成对应日期的最低气温与最高气温预测值；最后将预测值与测试集的真实气温值进行匹配，计算两者的误差并保存结果，以便后续模型性能评估。

python 复制代码 
# 5. 最低气温对应的模型训练
min_best_params = {'max_depth': 20, 'max_features': 1.0,
                   'max_samples': None, 'min_samples_leaf': 1,
                   'min_samples_split': 2, 'n_estimators': 300}
min_model = train_rf_model(X_train_min, y_train_min, min_best_params)
# 预测与结果保存
y_test_pred_min = predict_and_save_results(
    min_model, X_test_min, y_test_min, "最低气温"
)
# 最高气温对应的模型训练
max_best_params = {'max_depth': 20, 'max_features': 1.0,
                   'max_samples': None, 'min_samples_leaf': 1,
                   'min_samples_split': 2, 'n_estimators': 300}
max_model = train_rf_model(X_train_max, y_train_max, max_best_params)
# 预测与结果保存
y_test_pred_max = predict_and_save_results(
    max_model, X_test_max, y_test_max, "最高气温"
)

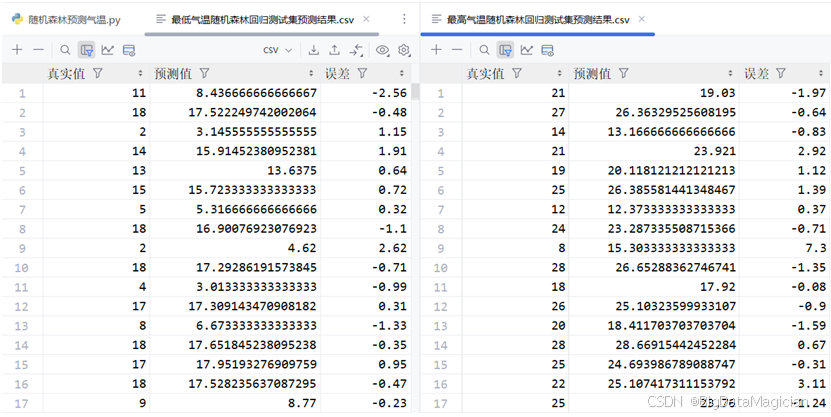
模型预测结果部分数据如图所示，可以看到最低气温和最高气温对应模型的真实值、预测值及误差值。

四、模型评估

1. 预测结果可视化

1.1 真实值与预测值数据可视化

本次可视化的核心目的是通过直观的图形方式，对比模型预测值与真实气温值的偏差程度，清晰呈现模型的预测精度与拟合效果，为后续模型性能评估提供直观的视觉依据。可视化所使用的数据为测试集对应的真实气温值（最低气温、最高气温）与模型输出的预测气温值，这些数据均来自模型预测结果。

可视化图形选择散点图作为可视化的核心图表类型，散点图能够直观展示每一组真实值与预测值的对应关系，便于观察数据点的分布规律；同时可在图中添加对角线作为理想拟合的参照线，数据点越贴近该线，说明预测值与真实值的偏差越小、模型拟合效果越好；相比单纯的数值表格，这种方式更易发现整体偏差趋势，也能识别出个别偏差较大的异常样本。

可视化过程如下代码所示，首先针对最低气温、最高气温两个预测任务，分别以真实气温值为横轴、预测气温值为纵轴绘制散点图；随后在图中添加红色对角线作为理想拟合参照线，并设置网格线以提升数据点的可读性；最后为图表添加标题、坐标轴标签，并完成可视化结果的保存。

python 复制代码 
def plot_prediction_comparison(y_true, y_pred, title, save_path):
    """
    绘制预测值与真实值对比散点图
    """
    plt.figure(figsize=(10, 8))
    plt.scatter(y_true, y_pred, alpha=0.6, color='blue', s=30)
    min_val, max_val = min(y_true.min(), y_pred.min()), max(y_true.max(), y_pred.max())
    plt.plot([min_val, max_val], [min_val, max_val], 'r--', alpha=0.8)
    plt.xlabel(f'{title}真实值', fontsize=14)
    plt.ylabel(f'{title}预测值', fontsize=14)
    plt.title(f'{title}真实值 vs 预测值', fontsize=14)
    plt.grid(True, alpha=0.3)
    plt.savefig(save_path)
    plt.close()
# 6. 预测结果可视化
# 最低气温真实值与预测值对比
plot_prediction_comparison(y_test_min, y_test_pred_min,
                           '最低温度', IMAGE_DIR / '最低温度预测对比.png')
# 最高气温真实值与预测值对比
plot_prediction_comparison(y_test_max, y_test_pred_max,
                           '最高温度', IMAGE_DIR / '最高温度预测对比.png')

从下图的可视化结果可以看到，最低气温的大部分散点集中在红色对角线附近，说明预测值与真实值的偏差较小，模型对最低气温的拟合效果较好；仅少数数据点偏离对角线，存在一定的预测误差，但整体处于可接受范围。

最高气温的散点同样呈现出贴近对角线的分布特征，表明模型对最高气温的预测精度较高；数据点的分布密度均匀，未出现系统性的偏差趋势，进一步验证了模型的稳定性。

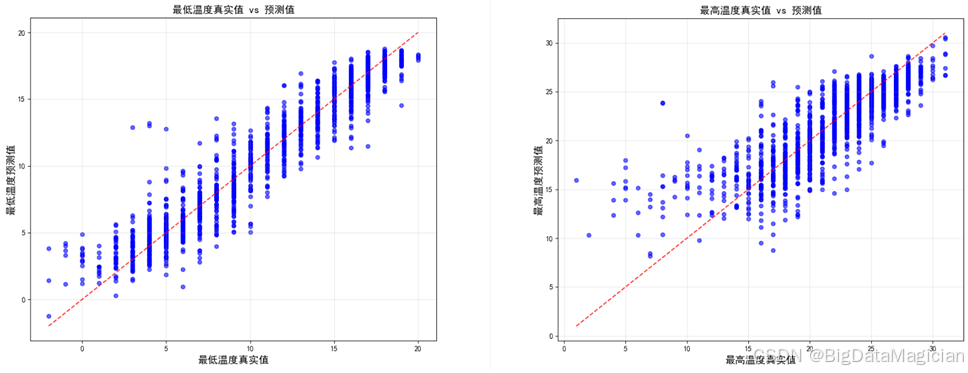
整体而言，散点图的直观展示表明，本研究构建的随机森林回归模型在气温预测任务中具备良好的拟合能力与预测精度，能够为昆明市气温趋势研判提供可靠的量化支撑。

1.2 误差分布数据可视化

本次可视化的核心目的是通过分析预测误差的分布形态，直观评估模型预测的稳定性与偏差特征，识别误差的集中区间与异常波动，为进一步优化模型提供依据。可视化所使用的数据为测试集真实气温值与模型预测值的差值，即最低气温预测误差与最高气温预测误差，数据均来自模型预测结果。

本次可视化选择直方图作为可视化的图表类型，它能通过直方图的柱状高度展示误差在不同区间的频数分布，同时在图中添加零误差参照线，清晰对比误差偏离零值的程度，比单纯的数值统计更直观地反映模型预测的精准度与稳定性。

可视化过程如下代码所示，首先针对最低气温、最高气温两个预测任务，分别计算每条测试样本的预测误差（真实值减去预测值）；随后以误差值为横轴、密度为纵轴绘制直方图，并在图中添加红色虚线作为零误差参照线，辅助观察误差的整体偏移情况；最后为图表添加标题、坐标轴标签与图例，并完成可视化结果的保存。

python 复制代码 
def plot_error_distribution(y_true, y_pred, title, save_path):
    """
    绘制预测误差分布图
    """
    plt.figure(figsize=(10, 6))
    errors = y_true - y_pred
    plt.hist(errors, bins=20, alpha=0.7, color='orange', edgecolor='black', density=True)
    plt.axvline(x=0, color='red', linestyle='--', label='零误差线')
    plt.title(f'{title}预测误差分布', fontsize=14)
    plt.xlabel('预测误差 (℃)', fontsize=14)
    plt.ylabel('密度', fontsize=14)
    plt.legend()
    plt.grid(alpha=0.3)
    plt.savefig(save_path)
    plt.close()
# 最低气温误差分布
plot_error_distribution(y_test_min, y_test_pred_min,
                        '最低气温', IMAGE_DIR / '最低气温预测误差分布.png')
# 最高气温误差分布
plot_error_distribution(y_test_max, y_test_pred_max,
                        '最高气温', IMAGE_DIR / '最高气温预测误差分布.png')

从下图的可视化结果可以看到，最低气温误差主要集中在-2℃2℃区间内，且直方图的峰值靠近零误差线，密度曲线呈近似正态分布形态，说明模型对最低气温的预测误差整体较小，且无明显的系统性偏差。最高气温误差主要集中在-3℃3℃区间内，峰值贴近零误差线，分布形态与最低气温误差类似，仅右侧存在少量偏差较大的样本，表明模型对最高气温的预测也具备较高的稳定性。

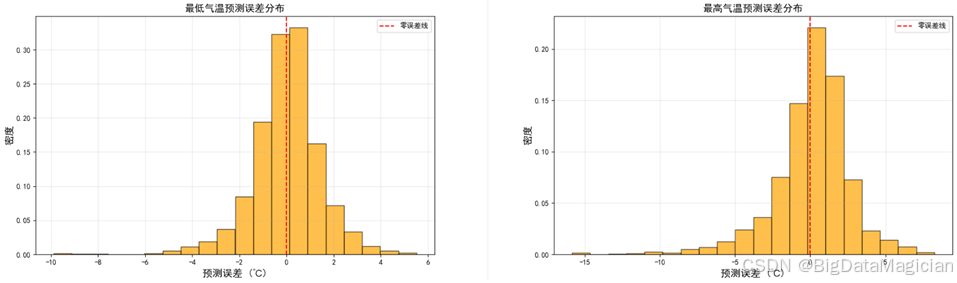
整体而言，误差分布直方图的直观展示表明，本研究构建的随机森林回归模型在气温预测任务中误差可控、分布合理，进一步验证了模型的可靠性。

2. 核心评估指标

本研究选取均方误差（MSE）、均方根误差（RMSE）与决定系数（R²）作为核心评估指标，这三项指标从不同维度构成了完整的模型性能评价体系；MSE 与 RMSE 侧重于量化预测值与真实值的偏差幅度，R² 则反映模型对数据变异的解释能力，三者结合可全面评估模型的精准度与拟合效果。

计算核心评估指标的主要目的是通过量化指标客观、全面地评估模型的预测性能，从误差大小与拟合程度两个维度衡量模型的精准度与解释力，为模型效果提供可量化的评价依据，同时也为后续模型优化提供数据支撑。

计算评估指标的过程如下代码所示，针对最低气温与最高气温两个预测任务，分别基于测试集的真实值与预测值完成指标计算；首先计算所有样本预测误差的平方平均值得到均方误差（MSE），再对 MSE 取平方根得到与气温量纲一致的均方根误差（RMSE），最后通过比较真实值与预测值的变异程度得到决定系数（R²）。

python 复制代码 
def evaluate_model(y_true, y_pred, target_name):
    """
    模型评估，返回核心指标
    """
    mse = mean_squared_error(y_true, y_pred)
    rmse = np.sqrt(mse)
    r2 = r2_score(y_true, y_pred)
    print(f'\n{target_name}核心评估指标：')
    print(f'均方误差(MSE)：{mse}')
    print(f'均方根误差(RMSE)：{rmse}')
    print(f'决定系数(R²)：{r2}')
    return mse, rmse, r2
# 7. 模型评估
# 核心评估指标
evaluate_model(y_test_min, y_test_pred_min, "最低气温")
evaluate_model(y_test_max, y_test_pred_max, "最高气温")

从下图的计算结果来看，最低气温预测模型的均方误差（MSE）为 2.116，均方根误差（RMSE）为 1.455℃，说明预测值与真实值的平均偏差约为 1.455℃；决定系数（R²）为 0.927，表明模型能够解释 92.7% 的最低气温变异，拟合效果良好。最高气温预测模型的均方误差（MSE）为 6.594，均方根误差（RMSE）为 2.568℃，预测值与真实值的平均偏差约为 2.568℃；决定系数（R²）为 0.699，说明模型能够解释 69.9% 的最高气温变异，拟合效果虽略逊于最低气温模型，但仍处于可接受范围。

整体而言，两项预测任务的核心评估指标均表明，本研究构建的随机森林回归模型具备较高的预测精度与拟合能力，能够满足昆明市气温趋势研判的需求。

3. 特征重要性数据可视化分析

3.1 特征重要性数据分析

本次分析的核心目的是识别对昆明市气温预测贡献度最高的日期衍生特征，明确不同特征在模型中的权重与作用，为后续特征优化与模型解释提供依据，同时也能进一步验证日期衍生属性作为预测特征的合理性。

分析过程如下代码所示，针对最低气温与最高气温两个预测模型，分别提取各输入特征的重要性权重，再按照权重从高到低排序，得到不同特征对气温预测的贡献度排序结果。这一过程基于随机森林模型的内置机制，通过计算特征在决策树分裂中的贡献度来量化其重要性。

python 复制代码 
# 特征重要性
feature_importance_min = get_feature_importance(min_model, FEATURES, "min")
feature_importance_max = get_feature_importance(max_model, FEATURES, "max")

分析结果如图所示，最低气温预测模型的季节（season）是最重要的特征，贡献度高达 55.95%，其次是年内天数（dayofyear），贡献度为 25.47%，其余特征的贡献度均低于 10%。这表明最低气温的变化与季节、年内天数的周期性关联最为紧密，符合气温随季节变化的客观规律。最高气温预测模型的季节（season）同样是最重要的特征，贡献度为 40.66%，年内天数（dayofyear）次之，贡献度为 25.59%，年份（year）也具有一定的贡献度（14.38%）。这说明最高气温的变化同样受季节与年内天数的主导，同时也存在一定的年际变化趋势。

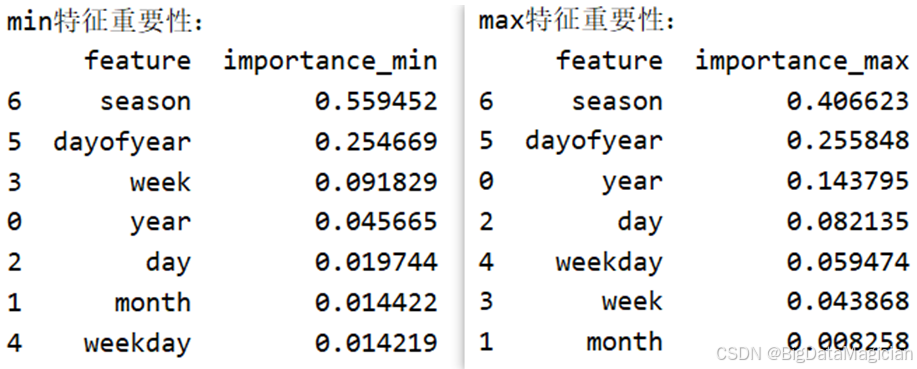
整体而言，两个模型的特征重要性结果均验证了季节与年内天数作为核心预测特征的合理性，也为后续进一步优化特征选择提供了明确方向。

3.2 特征重要性数据可视化

本次可视化的核心目的是通过直观的图形方式，清晰展示不同日期衍生特征在气温预测模型中的贡献度排序，让特征重要性的量化结果更易于解读，从而更直观地揭示各特征对气温预测的影响程度。可视化所使用的数据为最低气温与最高气温预测模型的特征重要性权重，这些权重来自对随机森林模型的特征贡献度计算结果。

可视化过程如下代码所示，首先针对最低气温、最高气温两个预测任务的特征重要性结果，分别构建包含特征名称与对应重要性得分的数据集；随后以特征名称为纵轴、重要性得分为横轴绘制水平条形图，通过条形长度直观反映各特征的贡献度大小；最后为图表添加标题、坐标轴标签，并完成可视化结果的保存。

python 复制代码 
def plot_feature_importance(importance_df, value_col, title, save_path):
    """
    绘制特征重要性条形图
    """
    plt.figure(figsize=(10, 8))
    sns.barplot(data=importance_df, x=value_col,
                y='feature', hue='feature',
                palette='viridis', legend=False)
    plt.title(title, fontsize=14)
    plt.xlabel('重要性得分', fontsize=14)
    plt.ylabel('特征名称', fontsize=14)
    plt.tight_layout()
    plt.grid(axis='x', alpha=0.5)
    plt.savefig(save_path)
    plt.close()
# 8. 特征重要性数据可视化分析
# 最低气温特征重要性
plot_feature_importance(feature_importance_min, 'importance_min',
                        '最低气温特征重要性', IMAGE_DIR / '最低气温特征重要性.png')
# 最高气温特征重要性
plot_feature_importance(feature_importance_max, 'importance_max',
                        '最高气温特征重要性', IMAGE_DIR / '最高气温特征重要性.png')
print("\n所有建模与可视化流程完成！结果已保存至 ./data 和 ./image 目录。")

可视化结果如下图所示，从可视化结果可以看到，最低气温特征重要性的"季节"特征的条形长度最长，显著高于其他特征，直观体现了其作为最核心预测特征的地位；"年内天数" 的条形长度次之，其余特征的条形长度均较短，进一步验证了最低气温变化与季节、年内天数的强关联。最高气温特征重要性的"季节" 同样是贡献度最高的特征，"年内天数" 与 "年份" 的条形长度也相对突出，清晰展示了这三类特征在最高气温预测中的主导作用。

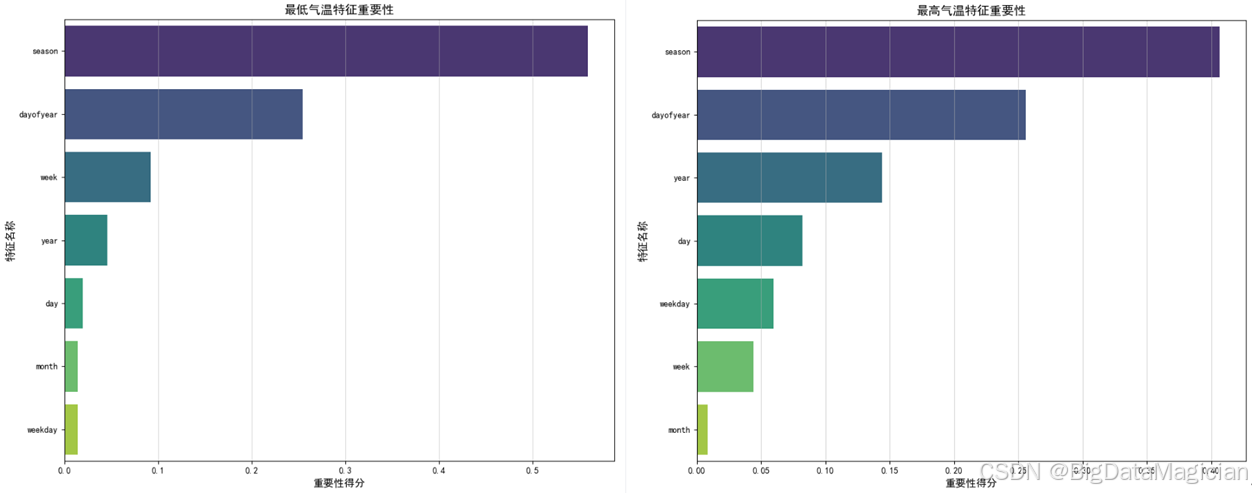
整体而言，水平条形图的直观展示让不同特征的贡献度差异一目了然，既验证了特征重要性的量化分析结果，也为后续特征优化提供了清晰的视觉依据。

五、完整代码

python 复制代码 
import warnings
from pathlib import Path

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split, GridSearchCV

# ==================== 全局配置（统一管理，避免重复设置） ====================
warnings.filterwarnings('ignore')

# 1. 绘图配置（统一中文字体，解决负号显示问题）
plt.rcParams['font.sans-serif'] = ['SimHei', 'WenQuanYi Zen Hei']
plt.rcParams['axes.unicode_minus'] = False

# 2. Pandas配置（优化数据显示）
pd.set_option('display.max_columns', None)
pd.set_option('display.width', None)
pd.set_option('display.max_colwidth', 50)
pd.set_option('display.expand_frame_repr', False)

# 3. 目录创建（一次性创建所需目录，避免分散创建）
DATA_DIR = Path('./data')
IMAGE_DIR = Path('./image')
DATA_DIR.mkdir(parents=True, exist_ok=True)
IMAGE_DIR.mkdir(parents=True, exist_ok=True)

# 4. 全局常量定义（便于后续修改）
FEATURES = ['year', 'month', 'day', 'week', 'weekday', 'dayofyear', 'season']
SEASON_MAPPING = {'春季': 0, '夏季': 1, '秋季': 2, '冬季': 3}
TEST_SIZE = 0.3
RANDOM_STATE = 42
CV_FOLDS = 5


# ==================== 工具函数（封装重复逻辑，减少代码冗余） ====================
def load_and_preprocess_data(raw_data_path):
    """
    加载原始数据并进行预处理（筛选昆明数据、日期转换、季节编码）
    """
    # 加载数据
    df = pd.read_csv(raw_data_path)
    # 季节编码
    df['season'] = df['season'].map(SEASON_MAPPING)
    return df


def calculate_correlation(df, features, target_col):
    """
    计算特征与目标变量的相关性并排序
    """
    corr_series = df[features].corrwith(df[target_col], method='spearman').sort_values(ascending=False)
    return corr_series


def plot_correlation_heatmap(df, features, title, save_path):
    """
    绘制特征相关性热力图（统一封装，避免重复代码）
    """
    corr_matrix = df[features].corr(method='spearman')
    mask = np.triu(m=np.ones_like(corr_matrix, dtype=bool), k=1)

    plt.figure(figsize=(10, 8))
    sns.heatmap(
        data=corr_matrix,
        mask=mask,
        annot=True,
        cmap='coolwarm',
        fmt='.2f',
        linewidths=0.5
    )
    plt.title(title, fontsize=14)
    plt.tight_layout()
    plt.savefig(save_path)
    plt.close()


def grid_search_best_params(X_train, y_train):
    """
    网格搜索寻找随机森林最优参数（统一参数网格，复用逻辑）
    """
    rf_model = RandomForestRegressor(random_state=RANDOM_STATE)
    # 定义参数网格
    param_grid = {
        'n_estimators': [100, 200, 300],
        'max_depth': [None, 10, 20, 30],
        'min_samples_split': [2, 5, 10],
        'min_samples_leaf': [1, 2, 4],
        'max_features': ['sqrt', 0.8, 1.0],
        'max_samples': [None, 0.8]
    }
    # 网格搜索配置
    grid_search = GridSearchCV(estimator=rf_model,
                               param_grid=param_grid, cv=5,
                               scoring='neg_mean_squared_error',
                               n_jobs=-1, verbose=1)

    # 训练并返回最优结果
    print("开始网格搜索参数优化...")
    grid_search.fit(X_train, y_train)

    best_model = grid_search.best_estimator_
    best_params = grid_search.best_params_
    best_neg_mse = grid_search.best_score_
    best_rmse = np.sqrt(-best_neg_mse)

    return best_params, best_neg_mse, best_rmse


def train_rf_model(X_train, y_train, params):
    """
    训练随机森林模型
    """
    model = RandomForestRegressor(**params, random_state=42)
    model.fit(X_train, y_train)
    return model


def predict_and_save_results(model, X_test, y_test, target_name):
    """
    模型预测并保存预测结果
    """
    # 预测
    y_test_pred = model.predict(X_test)

    # 保存测试集结果
    test_result_df = pd.DataFrame({
        "真实值": y_test,
        "预测值": y_test_pred,
        "误差": (y_test_pred - y_test).round(2)
    })
    test_save_path = DATA_DIR / f'{target_name}随机森林回归测试集预测结果.csv'
    test_result_df.to_csv(test_save_path, index=False)

    return y_test_pred


def evaluate_model(y_true, y_pred, target_name):
    """
    模型评估，返回核心指标
    """
    mse = mean_squared_error(y_true, y_pred)
    rmse = np.sqrt(mse)
    r2 = r2_score(y_true, y_pred)
    print(f'\n{target_name}核心评估指标：')
    print(f'均方误差(MSE)：{mse}')
    print(f'均方根误差(RMSE)：{rmse}')
    print(f'决定系数(R²)：{r2}')
    return mse, rmse, r2


def get_feature_importance(model, features, target_suffix):
    """
    获取并排序特征重要性
    """
    importance_df = pd.DataFrame({
        'feature': features,
        f'importance_{target_suffix}': model.feature_importances_
    })
    importance_df = importance_df.sort_values(by=f'importance_{target_suffix}', ascending=False)
    print(f'\n{target_suffix}特征重要性：\n{importance_df}')
    return importance_df


def plot_feature_importance(importance_df, value_col, title, save_path):
    """
    绘制特征重要性条形图
    """
    plt.figure(figsize=(10, 8))
    sns.barplot(data=importance_df, x=value_col,
                y='feature', hue='feature',
                palette='viridis', legend=False)
    plt.title(title, fontsize=14)
    plt.xlabel('重要性得分', fontsize=14)
    plt.ylabel('特征名称', fontsize=14)
    plt.tight_layout()
    plt.grid(axis='x', alpha=0.5)
    plt.savefig(save_path)
    plt.close()


def plot_prediction_comparison(y_true, y_pred, title, save_path):
    """
    绘制预测值与真实值对比散点图
    """
    plt.figure(figsize=(10, 8))
    plt.scatter(y_true, y_pred, alpha=0.6, color='blue', s=30)
    min_val, max_val = min(y_true.min(), y_pred.min()), max(y_true.max(), y_pred.max())
    plt.plot([min_val, max_val], [min_val, max_val], 'r--', alpha=0.8)
    plt.xlabel(f'{title}真实值', fontsize=14)
    plt.ylabel(f'{title}预测值', fontsize=14)
    plt.title(f'{title}真实值 vs 预测值', fontsize=14)
    plt.grid(True, alpha=0.3)
    plt.savefig(save_path)
    plt.close()


def plot_error_distribution(y_true, y_pred, title, save_path):
    """
    绘制预测误差分布图
    """
    plt.figure(figsize=(10, 6))
    errors = y_true - y_pred
    plt.hist(errors, bins=20, alpha=0.7, color='orange', edgecolor='black', density=True)
    plt.axvline(x=0, color='red', linestyle='--', label='零误差线')
    plt.title(f'{title}预测误差分布', fontsize=14)
    plt.xlabel('预测误差 (℃)', fontsize=14)
    plt.ylabel('密度', fontsize=14)
    plt.legend()
    plt.grid(alpha=0.3)
    plt.savefig(save_path)
    plt.close()


# ==================== 主业务逻辑（按流程拆分，清晰易懂） ====================
def main():
    # 1. 数据准备
    # 加载数据
    raw_data_path = '../数据预处理/data/昆明天气数据_清洗后.csv'
    df = pd.read_csv(raw_data_path, encoding='utf-8-sig')
    # 数据准备
    FEATURES = ['year', 'month', 'day', 'week', 'weekday', 'dayofyear', 'season']
    X = df[FEATURES]
    y_min = df['min_temperature']
    print(f"\n最低气温建模数据准备完成:")
    print(f"特征矩阵X形状: {X.shape}，目标变量y形状: {y_min.shape}")
    y_max = df['max_temperature']
    print(f"\n最高气温建模数据准备完成:")
    print(f"特征矩阵X形状: {X.shape}，目标变量y形状: {y_max.shape}")

    # 2. 季节特征编码
    SEASON_MAPPING = {'春季': 0, '夏季': 1, '秋季': 2, '冬季': 3}
    df['season'] = df['season'].map(SEASON_MAPPING)
    X = df[FEATURES]

    # 3. 数据集划分
    X_train_min, X_test_min, y_train_min, y_test_min = train_test_split(
        X, y_min, test_size=0.3, random_state=42, shuffle=True
    )
    print(f"最低气温训练集特征形状: {X_train_min.shape}，目标形状: {y_train_min.shape}")
    print(f"最低气温测试集特征形状: {X_test_min.shape}，目标形状: {y_test_min.shape}")
    print(f"最低气温训练集占比: {len(X_train_min) / len(y_min) * 100:.1f}%")
    print(f"最低气温测试集占比: {len(X_test_min) / len(y_min) * 100:.1f}%")

    X_train_max, X_test_max, y_train_max, y_test_max = train_test_split(
        X, y_max, test_size=0.3, random_state=42, shuffle=True
    )
    print(f"最高气温训练集特征形状: {X_train_max.shape}，目标形状: {y_train_max.shape}")
    print(f"最高气温测试集特征形状: {X_test_max.shape}，目标形状: {y_test_max.shape}")
    print(f"最高气温训练集占比: {len(X_train_max) / len(y_max) * 100:.1f}%")
    print(f"最高气温测试集占比: {len(X_test_max) / len(y_max) * 100:.1f}%")

    # 4. 网格搜索确定最优参数组合
    # min_best_params, min_best_neg_mse, min_best_rmse = grid_search_best_params(
    #     X_train_min, y_train_min)
    # print(f"\n最低气温最优参数组合: {min_best_params}")
    # print(f"最低气温最优交叉验证得分 (负MSE): {min_best_neg_mse:.4f}")
    # print(f"最低气温最优交叉验证得分 (RMSE): {min_best_rmse:.4f}")
    # max_best_params, max_best_neg_mse, max_best_rmse = grid_search_best_params(
    #     X_train_max, y_train_max)
    # print(f"\n最高气温最优参数组合: {max_best_params}")
    # print(f"最高气温最优交叉验证得分 (负MSE): {max_best_neg_mse:.4f}")
    # print(f"最高气温最优交叉验证得分 (RMSE): {max_best_rmse:.4f}")

    # 5. 最低气温对应的模型训练
    min_best_params = {'max_depth': 20, 'max_features': 1.0,
                       'max_samples': None, 'min_samples_leaf': 1,
                       'min_samples_split': 2, 'n_estimators': 300}
    min_model = train_rf_model(X_train_min, y_train_min, min_best_params)
    # 预测与结果保存
    y_test_pred_min = predict_and_save_results(
        min_model, X_test_min, y_test_min, "最低气温"
    )
    # 最高气温对应的模型训练
    max_best_params = {'max_depth': 20, 'max_features': 1.0,
                       'max_samples': None, 'min_samples_leaf': 1,
                       'min_samples_split': 2, 'n_estimators': 300}
    max_model = train_rf_model(X_train_max, y_train_max, max_best_params)
    # 预测与结果保存
    y_test_pred_max = predict_and_save_results(
        max_model, X_test_max, y_test_max, "最高气温"
    )

    # 6. 预测结果可视化
    # 最低气温真实值与预测值对比
    plot_prediction_comparison(y_test_min, y_test_pred_min,
                               '最低温度', IMAGE_DIR / '最低温度预测对比.png')

    # 最高气温真实值与预测值对比
    plot_prediction_comparison(y_test_max, y_test_pred_max,
                               '最高温度', IMAGE_DIR / '最高温度预测对比.png')

    # 最低气温误差分布
    plot_error_distribution(y_test_min, y_test_pred_min,
                            '最低气温', IMAGE_DIR / '最低气温预测误差分布.png')

    # 最高气温误差分布
    plot_error_distribution(y_test_max, y_test_pred_max,
                            '最高气温', IMAGE_DIR / '最高气温预测误差分布.png')

    # 7. 模型评估
    # 核心评估指标
    evaluate_model(y_test_min, y_test_pred_min, "最低气温")
    evaluate_model(y_test_max, y_test_pred_max, "最高气温")

    # 8. 特征重要性数据可视化分析
    # 特征重要性
    feature_importance_min = get_feature_importance(min_model, FEATURES, "min")
    feature_importance_max = get_feature_importance(max_model, FEATURES, "max")
    # 最低气温特征重要性
    plot_feature_importance(feature_importance_min, 'importance_min',
                            '最低气温特征重要性', IMAGE_DIR / '最低气温特征重要性.png')
    # 最高气温特征重要性
    plot_feature_importance(feature_importance_max, 'importance_max',
                            '最高气温特征重要性', IMAGE_DIR / '最高气温特征重要性.png')

    print("\n所有建模与可视化流程完成！结果已保存至 ./data 和 ./image 目录。")


# ==================== 程序入口 ====================
if __name__ == "__main__":
    main()
相关推荐
沐墨染12 小时前
黑词分析与可疑对话挖掘组件的设计与实现
前端·elementui·数据挖掘·数据分析·vue·visual studio code
Hcoco_me20 小时前
深度学习目标关联：常见深度学习匹配方法全面详解
人工智能·深度学习·分类·数据挖掘·自动驾驶
Aloudata1 天前
NoETL 指标平台与现有数据中台、治理体系的融合之道
数据仓库·数据分析·自动化·etl·noetl
Hcoco_me1 天前
目标追踪概述、分类
人工智能·深度学习·算法·机器学习·分类·数据挖掘·自动驾驶
babe小鑫1 天前
大专应用统计学专业学习数据分析的实用性分析
学习·数据挖掘·数据分析
Aloudata1 天前
企业级指标中台 API/JDBC 架构选型四步法
大数据·数据分析·etl·指标平台
SQL必知必会1 天前
SQL 数据分析终极指南
数据库·sql·数据分析
YangYang9YangYan2 天前
2026中专大数据与会计专业数据分析发展路径
大数据·数据挖掘·数据分析
热门推荐
01GitHub 镜像站点02Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services03爬虫逆向之观安（观镜WEB应用安全防护系统）04openClaw安装飞书插件｜核心踩坑：spawn EINVAL 错误终极解决指南05BongoCat - 跨平台键盘猫动画工具06HTB 赛季10 - Pterodactyl - user07UV安装并设置国内源08openclaw配置教程（linux+局域网ollama）09openclaw 配置飞书 报错 应用未建立长连接10243 行 microGPT：把“训练 + 推理”拆到骨头里