在前两篇文章中,我们掌握了线性回归和梯度下降的核心逻辑,但线性模型有个致命短板 ------ 只能处理 "直线能分开" 的简单问题。比如用重量和颜色区分苹果和橙子时,两类水果的分布可能是非线性的,线性回归根本 "分不明白"。
神经网络的出现就是为了突破这个限制,而反向传播则是让神经网络 "学会" 拟合非线性规律的核心算法。这篇文章会继续讲解讲清激活函数、交叉熵损失和反向传播的数学原理,彻底搞懂神经网络是怎么自我修正的。
一、先补基础:激活函数 ------ 给线性输出 "掰个弯"
神经网络能处理非线性问题,全靠激活函数。没有激活函数的神经网络,本质就是多层线性回归的叠加,依然解不了非线性问题。
1. 为什么需要激活函数?
线性回归的输出是 y = w1x1 + w2x2 + b,不管叠多少层,最终还是线性组合(比如 y = w3(w1x1 + b1) + b2 依然是线性的)。激活函数的作用,就是给线性输出加一个 "非线性变换",让网络能拟合弯曲的决策边界。
2. 最常用的激活函数:Sigmoid
我们以二分类场景(苹果 / 橙子)为例,重点讲 Sigmoid 函数:
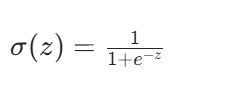
图像如下:
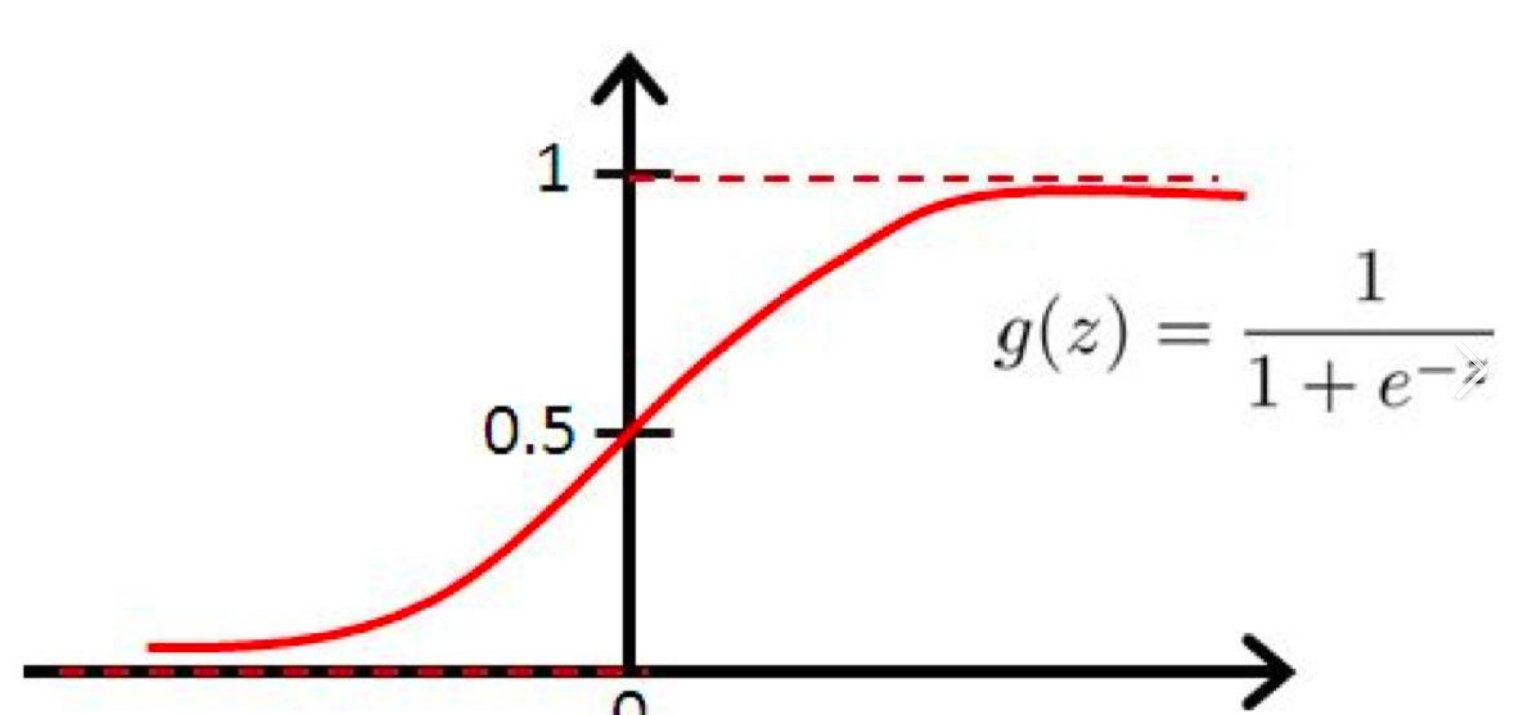
通俗解释:
- 输入
z可以是任意实数(比如线性层输出的-10或20),输出被压缩到0~1之间 ------ 刚好对应 "是苹果的概率"(0 = 肯定是橙子,1 = 肯定是苹果,或者说越接近0,越可能是橙子;越接近1,越可能是苹果)。 - 几何上看,Sigmoid 是一条 "S 型曲线",把原本的直线输出 "掰弯" 了,让网络能学习非线性边界。
关键:Sigmoid 的导数(反向传播要用)
反向传播需要计算梯度,Sigmoid 的导数有个极简形式:
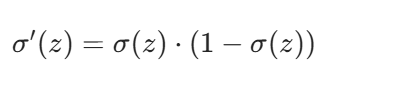
它的导数只和自身输出有关,计算起来特别快,这也是反向传播效率高的原因之一。
二、损失函数:交叉熵 ------ 精准衡量 "预测错得有多离谱"
训练神经网络的核心是 "减少预测误差",首先得定义 "误差怎么算"。分类问题不用线性回归的 MSE(均方误差),而是用交叉熵损失,因为它对分类问题的 "误差惩罚" 更合理。
1. 交叉熵损失的公式(二分类)
假设我们有 m 个样本,y_i 是真实标签(1 = 苹果,0 = 橙子),ŷ_i 是网络预测的 "是苹果的概率",交叉熵损失公式:
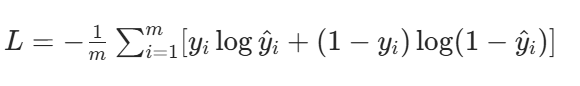
2. 通俗拆解:每一项都在 "惩罚错判"
我们分两种情况看:
- 真实标签是苹果(y_i=1) :公式只剩
-log(ŷ_i)。如果预测概率ŷ_i=0.9(几乎猜对),损失≈0.1;如果ŷ_i=0.1(严重错判),损失≈2.3------ 错得越离谱,损失越大,惩罚越重。 - 真实标签是橙子(y_i=0) :公式只剩
-log(1-ŷ_i)。如果预测概率ŷ_i=0.1(猜对),损失≈0.1;如果ŷ_i=0.9(错判成苹果),损失≈2.3------ 同样是 "错得越狠,罚得越重"。
对比:为什么不用 MSE?
MSE 对分类问题的 "惩罚太温和":比如把橙子错判成苹果(概率 0.9),MSE 的损失是 (0-0.9)²=0.81;而交叉熵损失是 -log(1-0.9)=2.3,能更快让网络意识到 "我错了,要修正"。当然,在本文的例子推导中,会继续使用MSE来展示求导过程及数值运算。
三、核心:反向传播 ------ 从结果倒推 "参数该怎么改"
反向传播的本质是链式法则的实战应用:从输出层的损失出发,倒着计算每一层参数的梯度(参数该改多少),然后用梯度下降更新参数。
我们以 "输入层(n维向量X)→隐藏层(3 个神经元)→输出层" 的两层神经网络为例,一步步拆解。
先明确前向传播流程(反向传播的前提)
先把数据 "往前传",算出预测结果,才能算损失、倒推梯度:
- 隐藏层计算:
Z1 = W1·X + b1→ 过 Sigmoid 激活:A1 = Sigmoid(Z1) - 输出层计算:
Z2 = W2·A1 + b2→ 过 Sigmoid 激活:ŷ = Sigmoid(Z2) - 计算损失:用MSE损失
L衡量ŷ和真实标签 y 的差距。
如表所示
| 层级 | 维度说明 | 核心公式(前向传播) |
|---|---|---|
| 输入层 | 单个样本输入 x∈Rd(d 为特征数) | X=[x1,x2,...,xd] |
| 隐藏层 | 神经元数量 h,激活函数 σ(⋅)(如 Sigmoid) | Z1=W1X+b1 A1=σ(Z1) |
| 输出层 | 回归任务输出单个值 y^,无激活函数 | Z2=W2A1+b2 y^=A2=Z2 |
我们要时刻记住,反向传播是为了给出如何减小损失函数的步骤。因此在本例中,实际上就是要给出L是如何随W1、b1、W2、b2变化的,即L对这几个变量的偏导数是什么。而求出这个偏导的过程,必须用到链式法则。





下面的过程都是在说明如何求出这四个偏导
反向传播:从损失倒推每一层的梯度
反向传播的核心是 "算梯度"------ 也就是 "参数改多少,损失能变小"。
步骤 1:算输出层的梯度
首先算损失对输出层线性值 Z2 的梯度:

有了这个梯度,就能算输出层参数(W2、b2)的梯度:

下面进行证明(这里实际上用到了矩阵导数,不过应该也是好理解的,这里假设了W2的维度方便观看形状):


步骤 2:算隐藏层的梯度

符号拆解:
W2^T:把输出层的梯度 "传回到" 隐藏层;⊙:按元素相乘(对应每个神经元的梯度);σ'(Z1):Sigmoid 的导数,修正梯度的大小。
有了 Z1 的梯度,隐藏层参数(W1、b1)的梯度就好算了:

步骤 3:参数更新(梯度下降)

反向传播的通俗总结
整个过程就像 "找错题原因":
- 先往前算(前向传播),得出 "预测结果" 和 "错题分数(损失)";
- 从错题分数倒推:先看输出层的参数(W2、b2)错在哪,再倒推隐藏层的参数(W1、b1)错在哪;
- 按错误程度修正参数,重复这个过程,直到损失越来越小、预测越来越准。
最后讨论一个问题:为什么线性回归不用反向传播?
在前两篇文章中,同样是梯度下降,线性回归为啥不用反向传播?核心原因是 "层数不同":
