数据结构二叉树—链式结构(中)

二叉树相关方法实现

二叉树节点个数的实现

方法1（错误示范）

复制代码

int TreeSize(BTNode* root)//方法1
{
	int size = 0;
	if (root == NULL)
	{
		return 0;
	}
	else
	{
		++size;
		TreeSize(root->left);
		TreeSize(root->right);
	}
	return size;
}
int main()
{
    BTNode* root = CreatBinaryTree();
    printf("TreeSize:%d\n", TreeSize(root));
}

为什么是1？因为我们的size初始化在函数的局部变量 ，出了这个函数的作用域，局部变量就还给了操作系统而每一次函数调用都会建立新的函数栈帧，每一个栈帧里面都有一个size，没有办法把每一个函数栈帧里面的size相加所以打印出来的结果就是1，所以现在我们就需要使用static 关键字把局部变量转化为静态局部变量，而静态局部变量在整个程序运行期间都不会释放，静态局部变量只能初始化一次且只能在本函数引用

复制代码

int TreeSize(BTNode* root)//方法1
{
	static int size = 0;
	if (root == NULL)
	{
		return 0;
	}
	else
	{
		++size;
		TreeSize(root->left);
		TreeSize(root->right);
	}
	return size;
}
int main()
{
    BTNode* root = CreatBinaryTree();
    printf("TreeSize:%d\n", TreeSize(root));
}

但是我们如果多打印几次

为什么变成这样了，就是因为现在size的是静态局部变量，所以每一次调用的时候它的值都不会再次初始化为0，依然会保留上一个值所以多次调用函数的时候就会将上一次的值相加，那现在我们就把局部变量改为全局变量试一下

复制代码

int size = 0;
int TreeSize(BTNode* root)
{
	
	if (root == NULL)
	{
		return 0;
	}
	else
	{
		++size;
		TreeSize(root->left);
		TreeSize(root->right);
	}
	return size;
}
int main()
{
    BTNode* root = CreatBinaryTree();
 size = 0;
printf("TreeSize:%d\n", TreeSize(root));
 size = 0;
printf("TreeSize:%d\n", TreeSize(root));
 size = 0;
printf("TreeSize:%d\n", TreeSize(root));
    return 0;
}

但是这个方法其实不是很好，并且代码太多了

方法2(地址传参)

上面的错误示范里面的变量除了函数不能发生改变那我们怎么才能让变量出了函数能够发生改变其实就可以用我们的传地址调用，因为地址传参在修改形参的时候也会影响实参，如果再带上递归就是每次调用函数自己时当前函数的形参和调用函数的形参的只是一样的，一直递归就能保证形参在被修改时最后返回的实参也会影响

复制代码

int TreeSize(BTNode* root,int* size)
{

	if (root == NULL)
	{
		return 0;
	}
	else
	{
		++(*size);
		TreeSize(root->left, size);
		TreeSize(root->right, size);
	}
	return *size;
}
int main()
{
    BTNode* root = CreatBinaryTree();
    int size=0;
    printf("TreeSize:%d\n", TreeSize(root,&size));
}

方法3(推荐)

其实我们可以用递归的思想来解决这个问题，我先左递归再右递归每一次递归都加1，最后再加上根节点就是我们最后的结点个数

复制代码

int TreeSize(BTNode* root)
{
	return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

二叉树叶子节点个数实现

当我们想要求出二叉树叶子节点个数的时候首先还是要判断是否为空树然后判断左子树和右子树是不是都是空树如果都是空树说明他就是叶子节点然后我们返回1，每一次调用都会判断这些情况所以就可以求出叶子节点个数

复制代码

int TreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	if (root->left == NULL && root->right == NULL)
		return 1;
	else
		return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
int main()
{
    BTNode* root = CreatBinaryTree();
    printf("TreeLeafSize:%d\n", TreeLeafSize(root));
}

二叉树深度实现

首先我们要求出二叉树的高度，我们就要分别把根节点左右子树的高度求出来然后取两者较大的值再加上1，就是根节点本身的高度

这样写可以，但是OJ过不了

复制代码

int TreeLeafHight(BTNode* root)//oj过不了,有效率问题
{
	if (root == NULL)
		return 0;
	else
		return  TreeLeafHight(root->left) > TreeLeafHight(root->right) ?
		TreeLeafHight(root->left) + 1 : TreeLeafHight(root->right) + 1;
}

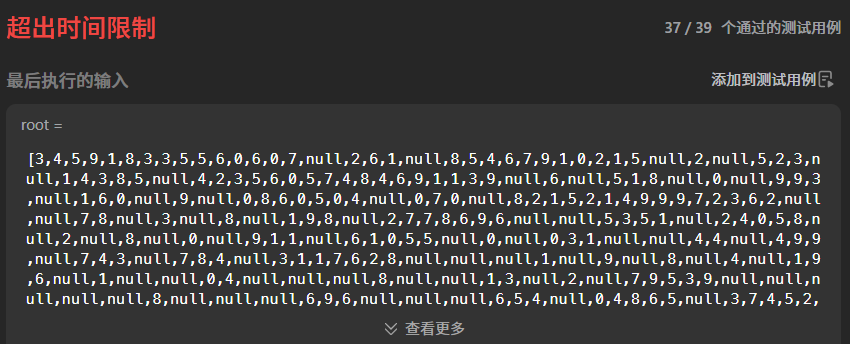
为什么会出现这种情况，这是因为刚刚我们提到的不管是判断两者谁大还是判断完后返回哪个都是用的函数调用 ，这样会导致我们好不容易递归完返回值后判断左子树高度和右子树高度谁大时，结果得到的还是返回函数调用，也就是说我们需要将上述的递归重新执行一遍并且每次到一个根节点都需要这样进行判断这样效率是非常低的，但出现这个情况的本质原因就在于我们没有对每次的左子树和右子树高度分别用两个变量进行记录从而导致重复调用函数

复制代码

int TreeLeafHight(BTNode* root)
{
	if (root == NULL)
		return 0;
	int leftHight = TreeLeafHight(root->left);
	int rightHight = TreeLeafHight(root->right);
	return return leftHight > rightHight ?leftHight + 1 : rightHight + 1;
}

现在用两个变量保存就可以解决问题了

二叉树第K层节点个数实现

首先求二叉树第k层结点个数其实和前面的求二叉树叶子结点个数有点类似，在求叶子结点个数中我们对如果是叶子结点的情况就返回1，所以在这里我们也用同样的方法：将满足在第k层的结点的情况返回1

复制代码

int TreeLeafKHight(BTNode* root, int k)
{
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	//子问题
	return TreeLeafKHight(root->left, k - 1) + TreeLeafKHight(root->right, k - 1);
}
int main()
{
    BTNode* root = CreatBinaryTree();
   printf("TreeLeafKHight:%d\n", TreeLeafKHight(root, 4));
}

二叉树查找值为X的节点

复制代码

BTNode* TreeFind(BTNode* root, HPDataType x)
{
	if (root == NULL)
		return;
	if (root->data)
		return root;
	 TreeFind(root->left, x);
     TreeFind(root->right, x);
}

或许大家会吸引这样的人但是这个代码是经典的错误， 因为函数在递归的时候它的返回值一定是返回上一个函数，这样写的目的就是直接让找到值的这个节点返回对外但是我们这个递归是返回到上一个函数，我们应该这样写

复制代码

BTNode* TreeFind(BTNode* root, HPDataType x)
{
	if (root == NULL)
		return;
	if (root->data==x)
		return root;
	BTNode* ret1 = TreeFind(root->left, x);
	if (ret1)
	{
		return ret1;
	}
	BTNode* ret2 = TreeFind(root->right, x);
	if (ret2)
	{
		return ret2;
	}
	return NULL;
}
int main()
{
	BTNode* root = CreatBinaryTree();
	
	BTNode* x = TreeFind(root, 3);
		printf("%d", x->data);
	return 0;
}