1. Clarke 变换
Clarke 变换是将三相静止坐标系中的电流(或电压)转换到两相静止坐标系( α \alpha α β \beta β坐标系),这种转换可以将三相系统的复杂性降低。
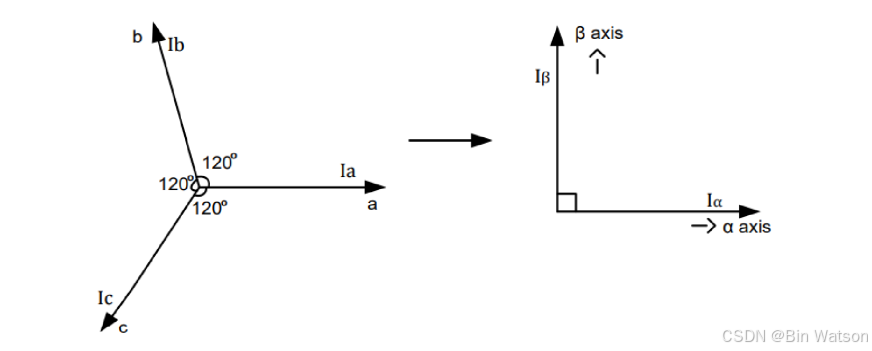
1.1 公式推导
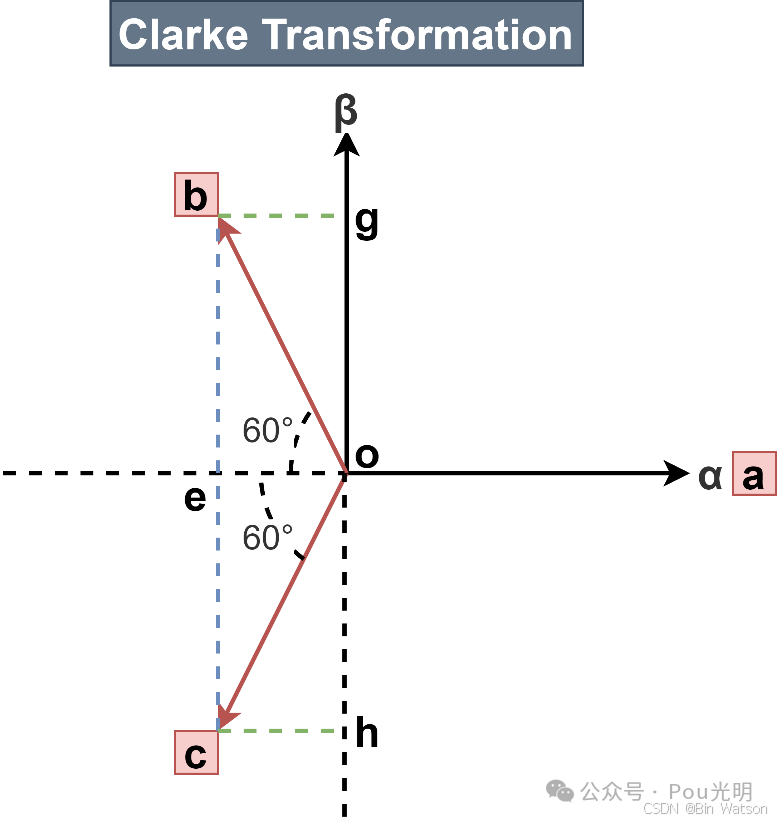
这里我们采用电压电流作为推导的基准,设三相电流分别为 i a i_a ia、 i b i_b ib 和 i c i_c ic ,计算这三个分量作用在 α \alpha α 轴、 β \beta β 轴上的值:
- i α i_\alpha iα:
- 作用在 α \alpha α 轴上面 I α = c o s 0 ° ∗ i a I_\alpha = cos0°\ *\ i_a Iα=cos0° ∗ ia
- 作用在 β \beta β 轴上面 I β = s i n 0 ° ∗ i a I_\beta = sin0°\ *\ i_a Iβ=sin0° ∗ ia
- i b i_b ib:
- 作用在 α \alpha α 轴上面 I α = c o s 120 ° ∗ i b I_\alpha = cos120°\ *\ i_b Iα=cos120° ∗ ib
- 作用在 β \beta β 轴上面 I β = s i n 120 ° ∗ i b I_\beta = sin120°\ *\ i_b Iβ=sin120° ∗ ib
- i c i_c ic:
- 作用在 α \alpha α 轴上面 I α = c o s ( − 120 ° ) ∗ i c I_\alpha = cos(-120°)\ *\ i_c Iα=cos(−120°) ∗ ic
- 作用在 β \beta β 轴上面 I β = s i n ( − 120 ° ) ∗ i c I_\beta = sin(-120°)\ *\ i_c Iβ=sin(−120°) ∗ ic
合并对应 α \alpha α 轴、 β \beta β ,得到代数形式:
{ I α = c o s 0 ° ∗ i a + c o s 120 ° ∗ i b + c o s ( − 120 ° ) ∗ i c I β = s i n 0 ° ∗ i α + s i n 120 ° ∗ i b + s i n ( − 120 ° ) ∗ i c \begin{cases} I_\alpha = cos0°\ *\ i_a\ +\ cos120°\ *\ i_b\ +\ cos(-120°)\ *\ i_c \\ I_\beta = sin0°\ *\ i_\alpha\ +\ sin120°\ *\ i_b\ +\ sin(-120°)\ *\ i_c \end{cases} {Iα=cos0° ∗ ia + cos120° ∗ ib + cos(−120°) ∗ icIβ=sin0° ∗ iα + sin120° ∗ ib + sin(−120°) ∗ ic
三角函数计算:
- c o s 0 ° = 1 cos0°\ =\ 1 cos0° = 1
- c o s 120 ° = − 1 2 cos120°\ =\ -\frac{1}{2} cos120° = −21
- c o s ( − 120 ° ) = c o s 240 ° = − 1 2 cos(-120°) = cos240°\ =\ -\frac{1}{2} cos(−120°)=cos240° = −21
- s i n 0 ° = 0 sin0°\ =\ 0 sin0° = 0
- s i n 120 ° = 3 2 sin120°\ =\ \frac{\sqrt{3}}{2} sin120° = 23
- s i n ( − 120 ° ) = s i n 240 ° = − 3 2 sin(-120°) = sin240°\ =\ -\frac{\sqrt{3}}{2} sin(−120°)=sin240° = −23
代入数值后,可得:
{ I α = i a − 1 2 i b − 1 2 i c I β = 3 2 i b − 3 2 i c \begin{cases} I_\alpha = i_a - \frac{1}{2}i_b - \frac{1}{2}i_c \\ I_\beta = \frac{\sqrt{3}}{2} i_b - \frac{\sqrt{3}}{2}i_c \end{cases} {Iα=ia−21ib−21icIβ=23 ib−23 ic
利用基尔霍夫电流定律,三相电流之和为零:
i a + i b + i c = 0 i c = − ( i a + i b ) \begin{matrix} i_a + i_b + i_c = 0 \\ i_c = -(i_a + i_b) \end{matrix} ia+ib+ic=0ic=−(ia+ib)
可以进一步将 i c i_c ic 化简,代入 i c = − ( i a + i b ) i_c = -(i_a + i_b) ic=−(ia+ib):
{ I α = i a − 1 2 i b − 1 2 ( − ( i a + i b ) ) I β = 3 2 i b − 3 2 ( − ( i a + i b ) ) \begin{cases} I_\alpha = i_a - \frac{1}{2}i_b - \frac{1}{2}(-(i_a + i_b)) \\ I_\beta = \frac{\sqrt{3}}{2} i_b - \frac{\sqrt{3}}{2}(-(i_a + i_b)) \end{cases} {Iα=ia−21ib−21(−(ia+ib))Iβ=23 ib−23 (−(ia+ib))
计算后可得:
{ I α = 3 2 i a I β = 3 2 i a + 3 i b \begin{cases} I_\alpha = \frac{3}{2}i_a \\ I_\beta = \frac{\sqrt{3}}{2} i_a + \sqrt{3}i_b \end{cases} {Iα=23iaIβ=23 ia+3 ib
在实际的电机 FOC 应用中,普遍都会期望让 I α I_\alpha Iα 和 3 2 i a \frac{3}{2}i_a 23ia 变化相等,也叫等幅值变化,其方式就是对 i a i_a ia、 i b i_b ib 和 i c i_c ic 先进行一个幅值 2 3 \frac{2}{3} 32 的变化,后到进行 Clarke 变化,这样就能实现 I α I_\alpha Iα 和 3 2 i a \frac{3}{2}i_a 23ia 幅值变化相等。
等幅值 Clarke 变化公式:
{ I α = i a I β = 3 3 i a + 2 3 3 i b \begin{cases} I_\alpha = i_a \\ I_\beta = \frac{\sqrt{3}}{3} i_a + \frac{2\sqrt{3}}{3}i_b \end{cases} {Iα=iaIβ=33 ia+323 ib
也可写成矩阵形式:
I α I β \] = \[ 1 0 3 3 2 3 3 \] \[ i a i b \] \\begin{bmatrix} I_\\alpha\\\\ I_\\beta \\end{bmatrix} = \\begin{bmatrix} 1\&0\\\\ \\frac{\\sqrt{3}}{3}\&\\frac{2\\sqrt{3}}{3} \\end{bmatrix} \\begin{bmatrix} i_a \\\\ i_b \\end{bmatrix} \[IαIβ\]=\[133 0323 \]\[iaib
2. 反(逆) Clarke 变换
反 Clarke 变换 将两相静止坐标系( α β \alpha\beta αβ 坐标系)中的电流或电压分量转换回三相静止坐标系(ABC 坐标系)的过程。

同样假设,在 α β \alpha\beta αβ 坐标系中, α \alpha α 轴和 β \beta β 轴上的电流分量分别为 I α I_α Iα 和 I β I_β Iβ 需要将它们转换回 ABC 坐标系中的电流分量 i a i_a ia、 i b i_b ib 和 i c i_c ic。
- I α I_\alpha Iα:
- 作用在 A 轴上面 i a = c o s 0 ° ∗ I α i_a= cos0° * I_\alpha ia=cos0°∗Iα
- 作用在 B 轴上面 i b = c o s 120 ° ∗ I α i_b = cos120° * I_\alpha ib=cos120°∗Iα
- 作用在 C 轴上面 i c = c o s ( 240 ° ) ∗ I α i_c = cos(240°) * I_\alpha ic=cos(240°)∗Iα
- I β I_\beta Iβ:
- 作用在 A 轴上面 i a = c o s 90 ° ∗ I β i_a= cos90° * I_\beta ia=cos90°∗Iβ
- 作用在 B 轴上面 i b = c o s ( 120 ° − 90 ° ) ∗ I β i_b = cos(120° - 90°) * I_\beta ib=cos(120°−90°)∗Iβ
- 作用在 C 轴上面 i c = c o s ( 240 ° − 90 ° ) ∗ I β i_c = cos(240° - 90°) * I_\beta ic=cos(240°−90°)∗Iβ
三角函数计算:
- c o s 0 ° = 1 cos0°=1 cos0°=1
- c o s 120 ° = − 1 2 cos120° = -\frac{1}{2} cos120°=−21
- c o s ( 240 ° ) = − 1 2 cos(240°) =-\frac{1}{2} cos(240°)=−21
- s i n 90 ° = 0 sin90°\ =\ 0 sin90° = 0
- c o s ( 120 ° − 90 ° ) = 3 2 cos(120° - 90°) = \frac{\sqrt{3}}{2} cos(120°−90°)=23
- c o s ( 240 ° − 90 ° ) = − 3 2 cos(240° - 90°) = -\frac{\sqrt{3}}{2} cos(240°−90°)=−23
代入数值后,可得:
{ i a = I α i b = − 1 2 I α + 3 2 I β i c = − 1 2 I α − 3 2 I β \begin{cases} i_a = I_\alpha\\ i_b= -\frac{1}{2}I_\alpha + \frac{\sqrt{3}}{2} I_\beta\\ i_c= -\frac{1}{2}I_\alpha -\frac{\sqrt{3}}{2} I_\beta\\ \end{cases} ⎩ ⎨ ⎧ia=Iαib=−21Iα+23 Iβic=−21Iα−23 Iβ
写成矩阵形式可得:
i a i b i c \] = \[ 1 0 − 1 2 3 2 − 1 2 − 3 2 \] \[ I α I β \] \\begin{bmatrix} i_a \\\\ i_b \\\\ i_c \\end{bmatrix} = \\begin{bmatrix} 1 \& 0 \\\\ -\\frac{1}{2} \& \\frac{\\sqrt{3}}{2} \\\\ -\\frac{1}{2} \& -\\frac{\\sqrt{3}}{2} \\end{bmatrix} \\begin{bmatrix} I_{\\alpha} \\\\ I_{\\beta} \\end{bmatrix} \\ iaibic = 1−21−21023 −23 \[IαIβ
3. Park 变换
Park 变换可以将电机从两相静止坐标系变换到随转子转动的坐标系(d-q轴)
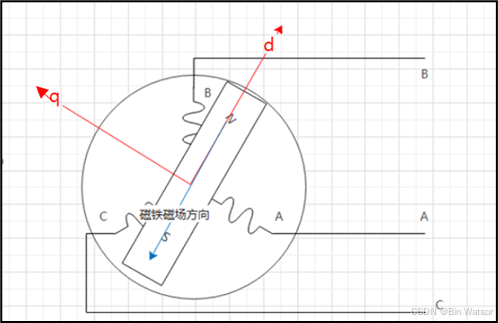
- d 轴(直轴):通常对齐转子永磁体的磁链方向(相当于 "磁场的北极方向");
- q 轴(交轴):垂直于 d 轴,是产生电磁转矩的核心轴(相当于 "推动转子转动的力的方向");
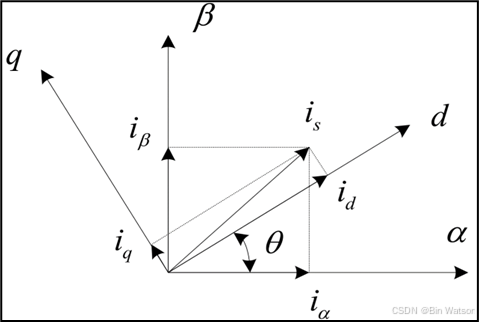
- i α i_\alpha iα:
- 作用在 d 轴上: i α c o s θ i_\alpha cos\theta iαcosθ
- 作用在 q 轴上: i α c o s ( π 2 + θ ) = − i α c o s θ i_\alpha cos(\frac{\pi}{2} + \theta) = -i_\alpha cos\theta iαcos(2π+θ)=−iαcosθ
- i β i_\beta iβ:
- 作用在 d 轴上: i β c o s ( π 2 − θ ) = i β s i n θ i_\beta cos(\frac{\pi}{2} - \theta) = i_\beta sin\theta iβcos(2π−θ)=iβsinθ
- 作用在 q 轴上: i β c o s θ i_\beta cos\theta iβcosθ
综上,可得 Park 变换的方程式:
{ i d = i α c o s θ + i β s i n θ i q = − i α c o s θ + i β c o s θ \begin{cases} i_d = i_\alpha cos\theta + i_\beta sin \theta\\ i_q = -i_\alpha cos\theta + i_\beta cos \theta \end{cases} {id=iαcosθ+iβsinθiq=−iαcosθ+iβcosθ
4. 反(逆) Park 变换
逆 Park 变换可以将电机从随转子转动的坐标系(d-q轴)变换到两相静止坐标系

- i d i_d id:
- 作用在 α \alpha α 轴上: i d c o s θ i_d cos\theta idcosθ
- 作用在 β \beta β 轴上: i d s i n θ i_d sin\theta idsinθ
- i q i_q iq:
- 作用在 α \alpha α 轴上: i q c o s ( π 2 − + θ ) = − i q s i n θ i_q cos(\frac{\pi}{2} -+\theta) = - i_q sin\theta iqcos(2π−+θ)=−iqsinθ
- 作用在 β \beta β 轴上: i q c o s θ i_q cos\theta iqcosθ
综上,可得逆 Park 变换的方程式:
{ i α = i d c o s θ − i q s i n θ i β = i d c o s θ + i q c o s θ \begin{cases} i_\alpha = i_d cos\theta - i_q sin \theta\\ i_\beta = i_d cos\theta + i_q cos \theta \end{cases} {iα=idcosθ−iqsinθiβ=idcosθ+iqcosθ
5. Matlab 公式仿真
【待补充】
参考
Clarke变换和Park变换及逆变换详解
FOC之Clarke变换原理及推导
FOC算法学习与实现笔记-01.克拉克变换
PARK变换与反PARK变换