优多元分层地理探测器模型(OMGD)研究

最优多元分层地理探测器模型(OMGD)研究

该研究针对传统地理探测器在多因子离散化、空间尺度效应分析上的不足，提出了最优多元分层地理探测器（OMGD） 模型，大幅提升了空间分层异质性（SSH）分析的能力。全文将按照论文结构逐部分解析，重点突出模型设计、方法论及实验验证环节。

一、论文基本信息

空间异质性（SH）是地理学第二定律，空间分层异质性（SSH） 指层内同质、层间异质的空间现象，地理探测器是分析SSH的经典方法，通过对比层内/层间方差评估自变量对因变量的解释力。

传统地理探测器存在三大核心问题：

1. 离散化方法局限：仅支持单/双因子离散化，三因子及以上仅能通过交互探测器实现，易导致层内样本不足；
2. 空间尺度效应分析单一：仅针对单因子进行尺度优化，未考虑多因子组合的尺度效应；
3. 离散化方案缺乏自动化：未整合多种分层方法实现单/多因子的最优离散化方案搜索。

为解决上述问题，研究提出OMGD模型，实现多因子组合的自动化最优离散化 和单/多因子的空间尺度最优选择，并通过多案例验证了模型的有效性。

二、研究基础与相关理论

2.1 空间分层异质性（SSH）

SSH的核心特征是层内方差小、层间方差大 ，地理探测器通过计算q统计量量化自变量对因变量的SSH解释力，q∈[0,1]，值越大表示解释力越强。

2.2 传统地理探测器的核心模块

传统地理探测器包含四大基础探测器，也是OMGD模型的基础组件：

1. 因子探测器：计算q统计量，评估单一自变量对因变量的解释力；
2. 交互探测器：分析两个自变量的交互作用对因变量的解释力（如协同增强、非线性减弱等）；
3. 风险探测器：通过t检验分析不同层间因变量的均值差异显著性；
4. 生态探测器：通过F检验比较两个自变量对因变量解释力的差异显著性。

2.3 分层方法分类

论文将SSH分析的分层方法分为四类，OMGD模型重点整合了前两类：

1. 单变量分层法：等距、分位数、自然断裂、几何间隔、标准差（共5种，传统模型常用）；
2. 聚类基分层法：K-means、二分K-means、层次聚类、谱聚类、高斯混合模型（GMM）（共5种，OMGD新增）；
3. 多准则分层法：融合空间连通性约束的分层方法；
4. 监督分层法：基于决策树、q统计量的分层方法。

2.4 传统优化模型（OPGD）

Song et al. (2020)提出的最优参数地理探测器（OPGD） 是OMGD的重要参考，OPGD实现了单因子的自动化离散化和空间尺度优化，但仅支持单因子尺度分析，且离散化方法仅含单变量分层法，无法处理多因子组合。

三、OMGD模型设计与方法论（核心部分）

OMGD模型在传统地理探测器和OPGD模型基础上，新增因子离散化优化模块 和尺度探测器模块 ，整体包含六大核心组件：因子离散化优化、尺度探测器、因子探测器、交互探测器、风险探测器、生态探测器。模型整体框架如图1所示：

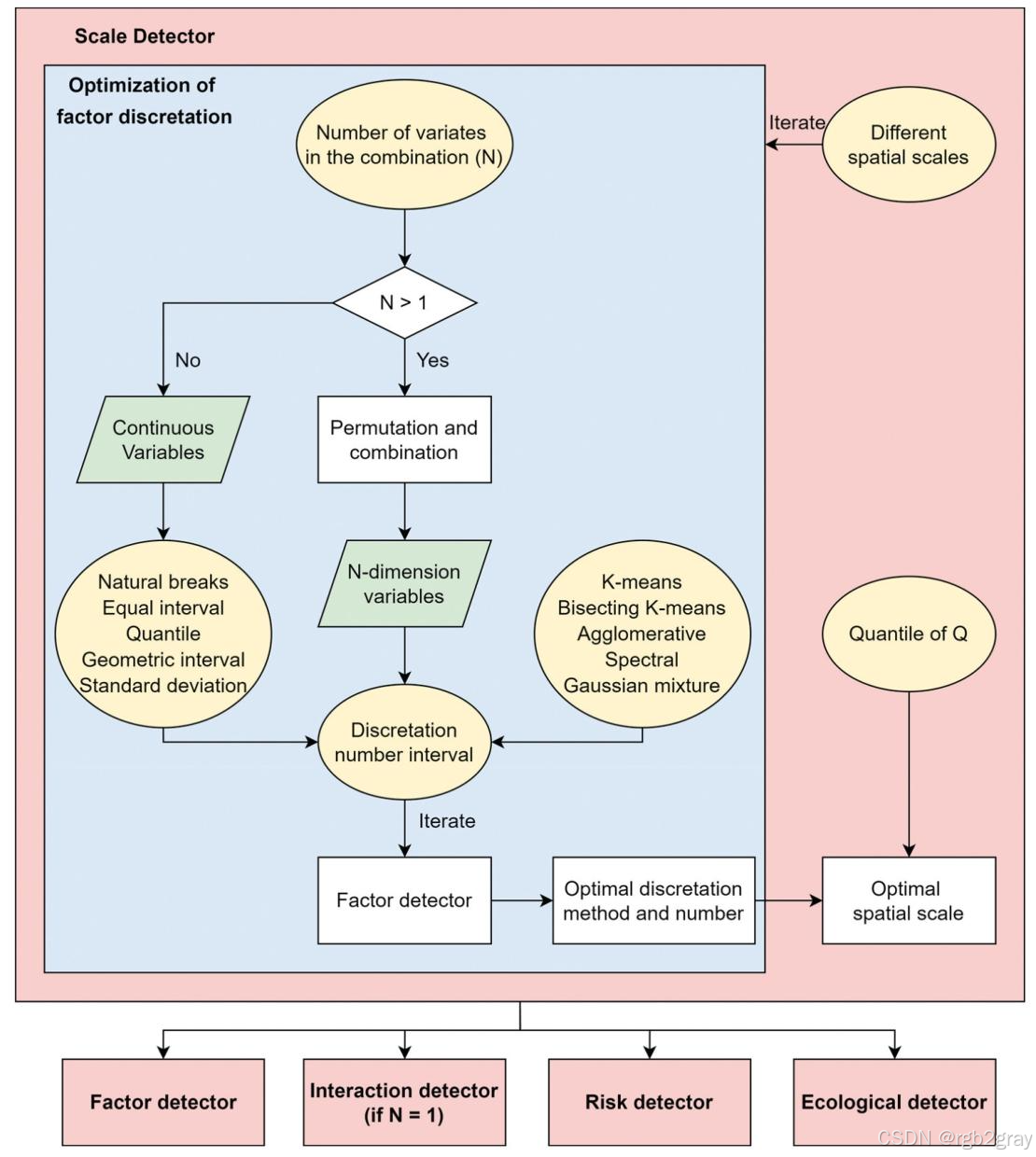
图1 OMGD模型原理图：核心为因子离散化优化和尺度探测器，结合四大基础探测器实现单/多因子的SSH分析

3.1 因子探测器（Factor Detector）

因子探测器是OMGD的核心量化组件，通过q统计量 和F检验评估自变量（单/多因子组合）对因变量的解释力，是离散化优化和尺度分析的基础。

3.1.1 q统计量计算公式

Q=1−∑h=1LNhσh2/Nσ2Q=1-\sum_{h=1}^{L} N_{h} \sigma_{h}^{2} / N \sigma^{2}Q=1−h=1∑LNhσh2/Nσ2

• 符号说明：LLL为分层数，NhN_hNh为第hhh层的样本数，σh2\sigma_h^2σh2为第hhh层因变量的方差，NNN为总样本数，σ2\sigma^2σ2为因变量总方差；
• 物理意义：q值越大，说明自变量的分层能更好地解释因变量的空间异质性，q=1表示完全解释，q=0表示无解释力。

3.1.2 显著性检验（非中心F分布）

通过F检验验证q统计量的显著性（p<0.05p<0.05p<0.05），计算公式：
F=N−LL−1×Q1−Q∼F(L−1,N−L,λ)F=\frac{N-L}{L-1} × \frac{Q}{1-Q} \sim F(L-1, N-L, \lambda)F=L−1N−L×1−QQ∼F(L−1,N−L,λ)

其中非中心性参数λ\lambdaλ：
λ=[∑h=1LYh‾2−1N(∑h=1LYh‾Nh)2]/σ2\lambda=\left[\sum_{h=1}^{L}{\overline{Y_{h}}}^{2}-\frac{1}{N}\left(\sum_{h=1}^{L} \overline{Y_{h}} \sqrt{N_{h}}\right)^{2}\right] / \sigma^{2}λ= h=1∑LYh2−N1(h=1∑LYhNh )2 /σ2
Yh‾\overline{Y_h}Yh为第hhh层因变量的均值，通过Python的scipy包实现F检验。

3.2 因子离散化优化模块（Optimization of Factor Discretization）

这是OMGD的核心创新之一 ，实现单因子 和多因子组合 的自动化最优离散化，核心目标是找到使q统计量最大且通过显著性检验的分层方法+分层数 组合。模块整合了5种单变量分层法+5种聚类基分层法，并通过z-score标准化消除量纲影响。

3.2.1 单因子离散化优化

1. 输入：连续型地理自变量、因变量；
2. 分层数区间：默认3~7（可自定义）；
3. 遍历：对5种单变量+5种聚类基分层法，遍历所有分层数，计算各方案的q值；
4. 筛选：选择q值最大且p<0.05p<0.05p<0.05的方案作为最优离散化方案；
5. 实现函数：OMGD的classify+factor_detector函数，可视化函数classify_plot。

3.2.2 多因子组合离散化优化（OMGD核心突破）

针对≥2的因子组合，解决了传统模型仅能通过交互探测器处理多因子的问题，步骤如下：

1. 因子组合：对所有自变量进行排列组合，生成多因子组合（如双因子、三因子、四因子及以上）；
2. 量纲消除 ：对每个组合内的所有因子进行z-score标准化，避免量纲差异影响聚类结果；
3. 分层方法 ：因多因子无法使用单变量分层法，仅遍历5种聚类基分层法；
4. 分层数遍历：默认3~7，计算各方案的q值；
5. 筛选 ：选择q值最大且p<0.05p<0.05p<0.05的方案作为最优离散化方案；
6. 可视化 ：≤3因子的组合可通过classify_plot可视化，≥4因子因维度限制无法可视化，但可通过风险探测器验证分层有效性。

3.2.3 聚类基分层法的细节实现

OMGD在Python中基于scikit-learn实现5种聚类基分层法，针对大数据集做了优化：

1. K-means/二分K-means ：初始化用kmeans++加速，样本数>10000时用Mini Batch K-means减少计算量；
2. 层次聚类（Agglomerative） ：采用自底向上的合并策略，连通性约束设为single以提升计算效率；
3. 谱聚类（Spectral） ：通过pyamg的代数多重网格求解特征值问题，提升复杂数据结构的聚类效果；
4. 高斯混合模型（GMM）：基于EM算法拟合，支持非凸聚类，适配复杂地理数据的分布特征。

3.3 尺度探测器模块（Scale Detector）

OMGD的第二个核心创新 ，实现单因子+多因子组合 的最优空间尺度自动识别，解决了传统模型仅支持单因子尺度分析的问题。

3.3.1 空间尺度的定义

地理研究中的空间尺度指观测单元的粒度（如250m、500m、1000m网格），不同尺度下自变量对因变量的解释力存在显著差异（尺度效应）。

3.3.2 最优尺度的判定准则

以q值的分位数均值 为判定标准（默认80%分位数，可自定义），即选择使高解释力因子/组合的平均q值最大的空间尺度为最优尺度，理由：高q值的因子/组合更能反映因变量的SSH特征。

3.3.3 尺度探测器的实现步骤

1. 构建多尺度网格：生成不同粒度的空间网格（如论文中250m、500m、...、2000m）；
2. 重采样 ：将所有自变量/因变量重采样到各尺度网格，采用分区统计平均方法；
3. 离散化优化：对每个尺度下的单因子/多因子组合，执行3.2节的离散化优化，得到各方案的最优q值；
4. 计算分位数均值：对每个尺度，提取所有因子/组合的最优q值，计算指定分位数（如80%）的均值；
5. 筛选最优尺度 ：选择分位数均值最大的尺度为最优空间尺度；
6. 实现函数 ：OMGD的scale_detector函数，可视化函数scale_plot。

3.4 交互探测器（Interaction Detector）

OMGD的交互探测器在传统基础上做了适配，仅针对单因子（多因子组合因分层复杂暂不支持），步骤如下：

1. 对两个自变量A、B，分别采用其最优离散化方案进行分层，分层数为LAL_ALA、LBL_BLB；
2. 对A、B的分层进行叠加，得到新的分层，分层数介于max(LA,LB)max(L_A,L_B)max(LA,LB)和LA×LBL_A×L_BLA×LB之间；
3. 计算叠加后分层的q值，与单一因子的q值对比，判断交互类型：非线性增强、双因子增强、单因子减弱、非线性减弱、独立；
4. 实现函数：interaction_detector。

3.5 风险探测器（Risk Detector）

用于验证离散化分层的有效性，分析不同层间因变量的均值差异是否显著，步骤如下：

1. 计算每个分层内因变量的均值Yi‾\overline{Y_i}Yi、Yj‾\overline{Y_j}Yj和方差si2s_i^2si2、sj2s_j^2sj2；
2. 通过t检验 验证两层间均值的显著性（p<0.05p<0.05p<0.05），t统计量公式：
   tYi‾−Yj‾=(Yi‾−Yj‾)/si2/Ni+sj2/Njt_{\overline{Y_{i}}-\overline{Y_{j}}}=\left(\overline{Y_{i}}-\overline{Y_{j}}\right) / \sqrt{s_{i}^{2} / N_{i}+s_{j}^{2} / N_{j}}tYi−Yj=(Yi−Yj)/si2/Ni+sj2/Nj
3. 自由度dfdfdf计算公式：
   df=(si2/Ni+sj2/Nj)/[1Ni−1(si2/Ni)2+1Nj−1(sj2/Nj)2]d f=\left(s_{i}^{2} / N_{i}+s_{j}^{2} / N_{j}\right) /\left[\frac{1}{N_{i}-1}\left(s_{i}^{2} / N_{i}\right)^{2}+\frac{1}{N_{j}-1}\left(s_{j}^{2} / N_{j}\right)^{2}\right]df=(si2/Ni+sj2/Nj)/[Ni−11(si2/Ni)2+Nj−11(sj2/Nj)2]
4. 结果解读：若层间t检验显著，说明离散化分层能有效区分因变量的空间分布；
5. 实现函数：risk_detector，可视化函数risk_plot。

3.6 生态探测器（Ecological Detector）

用于比较两个自变量/因子组合对因变量的解释力是否存在显著差异，步骤如下：

1. 计算两个自变量u、v的层内总方差∑h=1LuNu,hσu,h2\sum_{h=1}^{L_u} N_{u,h} \sigma_{u,h}^2∑h=1LuNu,hσu,h2和∑h=1LvNv,hσv,h2\sum_{h=1}^{L_v} N_{v,h} \sigma_{v,h}^2∑h=1LvNv,hσv,h2；
2. 通过F检验 验证差异显著性（p<0.05p<0.05p<0.05），F统计量公式：
   F=Nu(Nv−1)∑h=1LuNu,hσu,h2Nv(Nu−1)∑h=1LvNv,hσv,h2F=\frac{N_{u}\left(N_{v}-1\right) \sum_{h=1}^{L_{u}} N_{u, h} \sigma_{u, h}^{2}}{N_{v}\left(N_{u}-1\right) \sum_{h=1}^{L_{v}} N_{v, h} \sigma_{v, h}^{2}}F=Nv(Nu−1)∑h=1LvNv,hσv,h2Nu(Nv−1)∑h=1LuNu,hσu,h2
3. 结果解读：若F检验显著，说明两个自变量的解释力存在显著差异；
4. 实现函数：ecological_detector，可视化函数ecological_plot。

四、实验设计与数据来源

研究通过三类实验数据 验证OMGD模型的有效性，分别为案例应用数据（深圳城市热环境） 、模型对比基准数据（OPGD的NDVI变化+H1N1流感数据） 、模拟数据 ，同时设置离散化分层数3~7为统一参数。

4.1 案例应用数据：深圳城市热环境（核心验证）

4.1.1 研究区与因变量

• 研究区：中国深圳市；
• 因变量：地表温度（LST），来源于2023年Landsat 9 OLI-2/TIRS-2数据，空间分辨率30m，取年最大值。

4.1.2 自变量（6个地理因子）

共6个影响城市热环境的核心因子，数据来源与预处理如下表：

变量名	含义	数据来源	空间分辨率	预处理
NDVI	植被覆盖度	Landsat 9	30m	年最大值，归一化计算
NDBI	建筑用地指数	Landsat 9	30m	年最大值，归一化计算
MNDWI	改进型水体指数	Landsat 9	30m	年最大值，归一化计算
DEM	数字高程模型	Copernicus DEM GLO-30	30m	原始高程
Built	建筑表面密度	GHSL全球建筑数据	10m	重采样至30m，网格平均
Roads	道路核密度	Open Street Map 2023	30m	核密度分析，网格平均

4.1.3 多尺度网格构建

生成6种粒度的网格：250m、500m、750m、1000m、1500m、2000m，将所有变量重采样到各尺度网格，用于尺度探测器分析。

4.2 模型对比基准数据

采用OPGD模型（Song et al. 2020）的两类经典数据，用于对比OMGD与OPGD的尺度优化 和因子探测器性能：

1. NDVI变化数据：因变量为NDVI变化，自变量含气候区、降水、温度变化等6个因子，空间尺度50~50km；
2. H1N1流感数据：因变量为H1N1流感发病率，自变量含温度、降水、人口密度等10个因子，空间尺度50~150km。

4.3 模拟数据

用于验证OMGD在不同数据分布下的离散化优化效果，设置3组样本量（300、500、700），特征如下：

1. 因变量：服从正态分布（均值0，标准差10）；
2. 自变量：3个，分别服从t分布（30自由度） 、均匀分布 、伽马分布（均值0，标准差10）；
3. 变量关系：因变量与t分布自变量为线性关系，与均匀分布为多项式关系，与伽马分布为指数关系。

五、实验结果与分析

研究从尺度探测器结果 、因子离散化优化+风险探测器结果 、四大基础探测器结果 、OMGD与OPGD对比四个维度展开分析，核心验证OMGD的多因子离散化和尺度分析能力。

5.1 尺度探测器结果：深圳LST的最优空间尺度

对单因子、双因子组合、三因子组合分别计算80%分位数的q值均值，结果如图4：

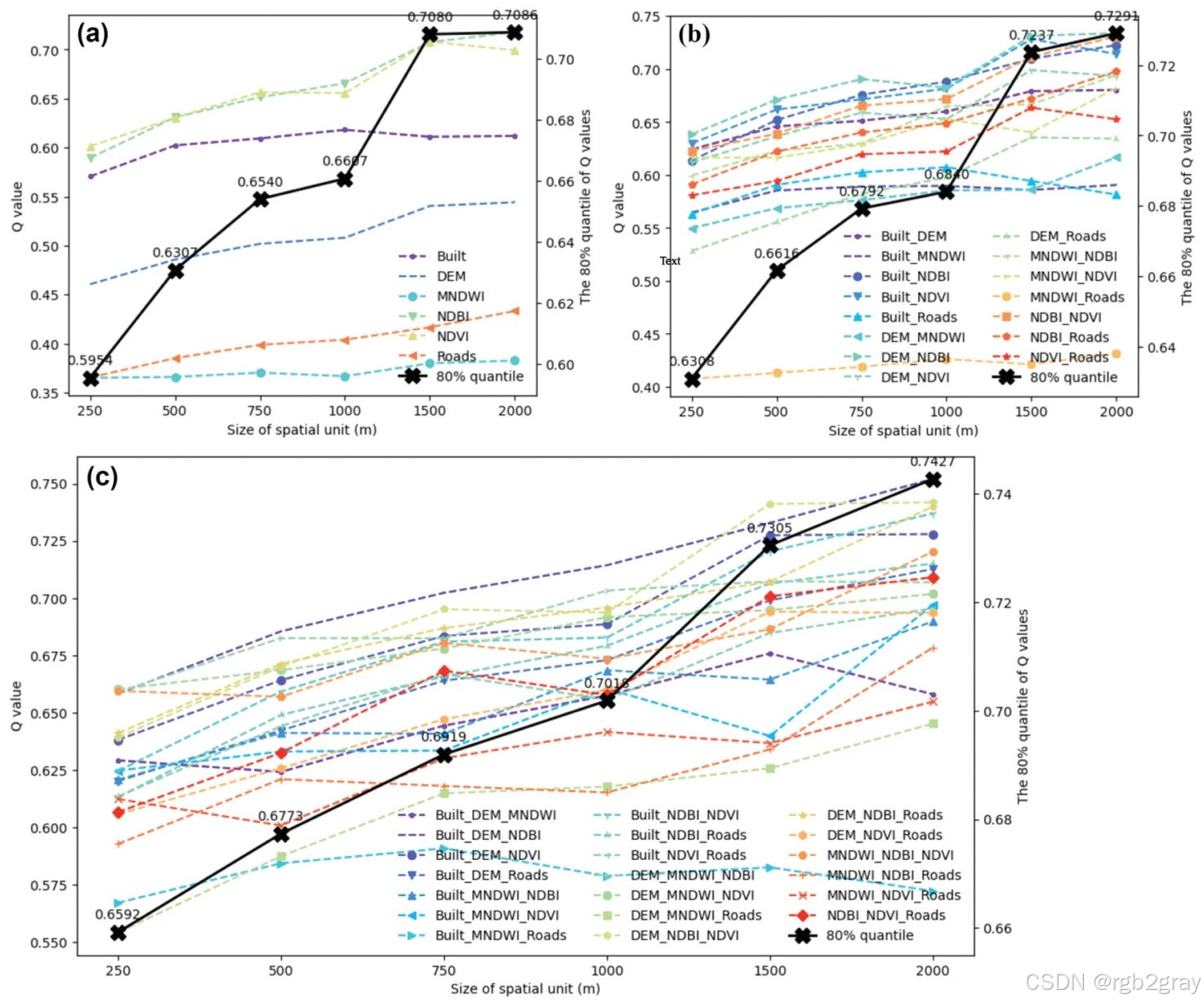
图4 深圳LST基于q值80%分位数的尺度探测器结果：(a)单因子 (b)双因子组合 ©三因子组合

结果解读：

1. 单因子：q值均值从250m逐步上升至1500m，1500~2000m趋于稳定；
2. 双因子组合：变化趋势与单因子一致，1500m后趋于稳定；
3. 三因子组合：q值均值在250~2000m持续上升；
4. 最优尺度 ：综合选择2000m为深圳LST SSH分析的最优空间尺度，后续所有分析均基于2000m网格。

5.2 因子离散化优化+风险探测器结果

基于2000m最优尺度，对单因子、双因子组合、三因子组合、≥4因子组合分别进行离散化优化，并通过风险探测器验证分层有效性，核心结果如下：

5.2.1 单因子（图5）

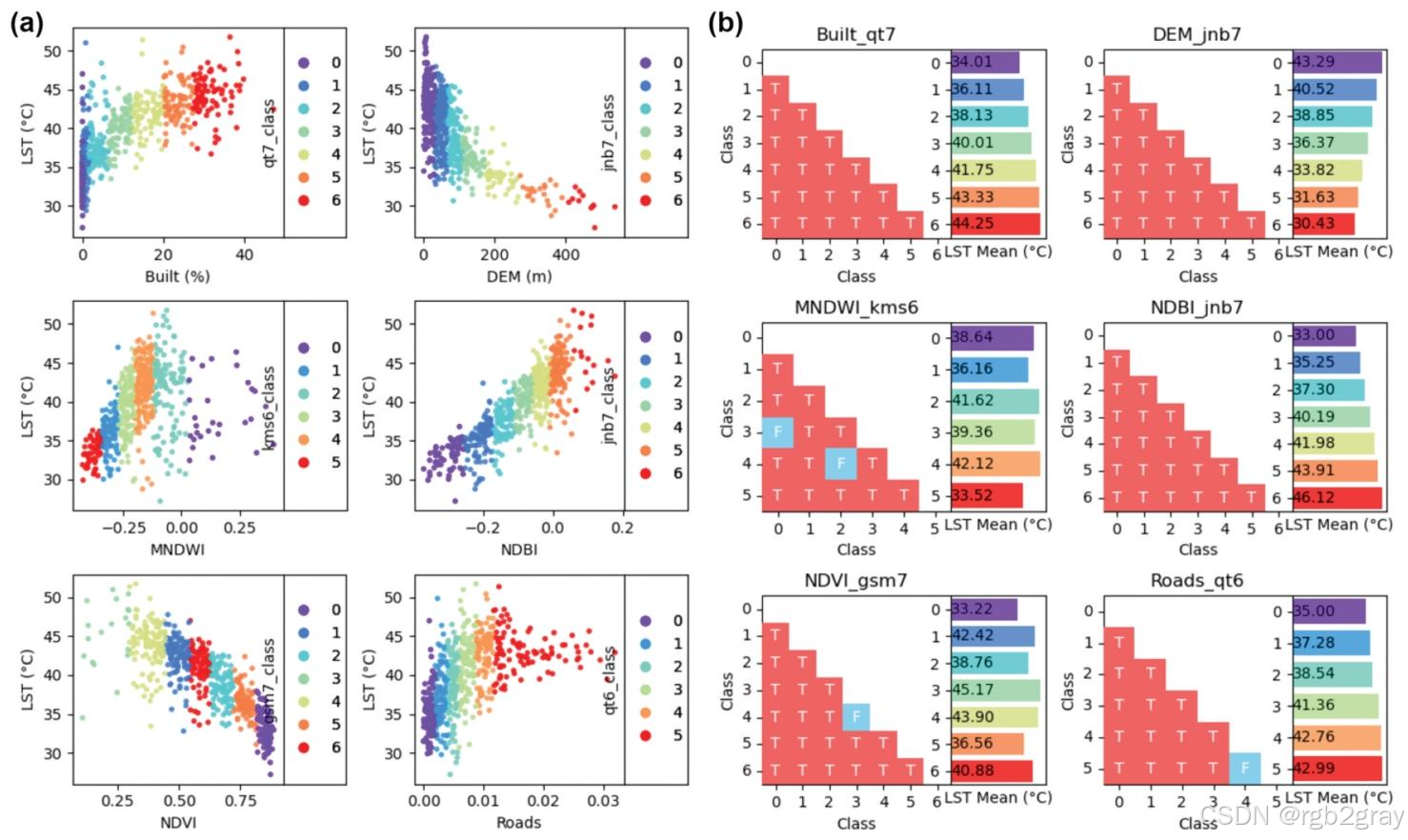
图5 单因子最优离散化(a)与风险探测器(b)结果：不同颜色为分层，次坐标轴为最优方法+分层数

关键结果：

1. 最优分层方法：分位数（qt）和自然断裂（jnb）为最常用方法；
2. 最优分层数：6个因子中4个为7层，2个为6层；
3. 变量相关性：Built、MNDWI、NDBI、Roads与LST正相关 ，DEM、NDVI与LST负相关；
4. 风险探测器：绝大多数层间t检验显著（p<0.05p<0.05p<0.05），离散化方案有效。

5.2.2 双因子组合（图6）

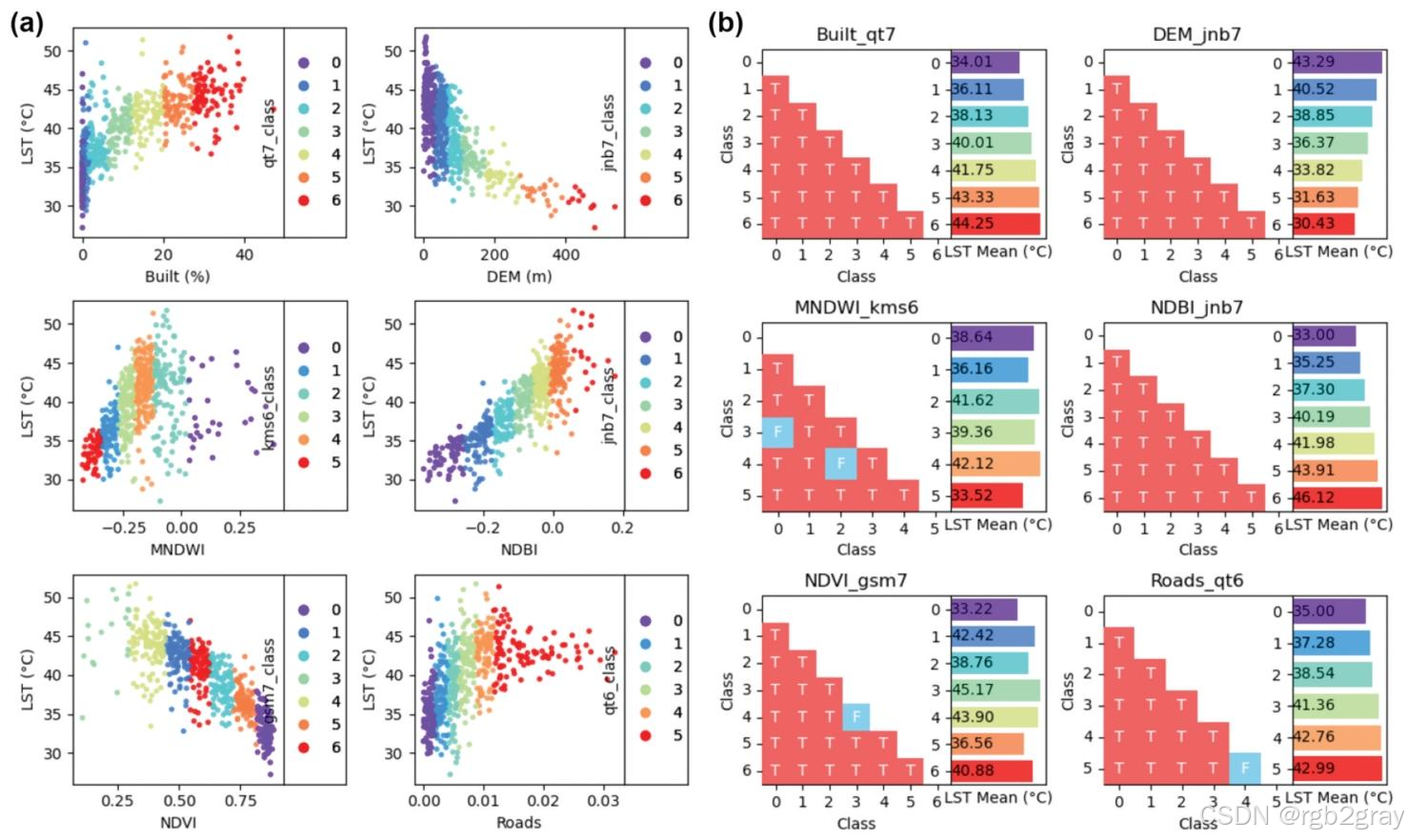
图6 双因子组合最优离散化(a)与风险探测器(b)结果：x/y轴为两个因子，不同颜色为聚类分层

关键结果：

1. 最优分层数：绝大多数为7层；
2. 最优聚类方法：二分K-means（bkm）占比最高（7次），其次为GMM（4次）、K-means（3次）；
3. 风险探测器：层间LST均值差异显著，聚类分层能有效捕捉双因子的组合特征（如Built+DEM组合中，低建筑密度区按高程分层，高建筑密度区按密度分层）。

5.2.3 三因子组合（图7）

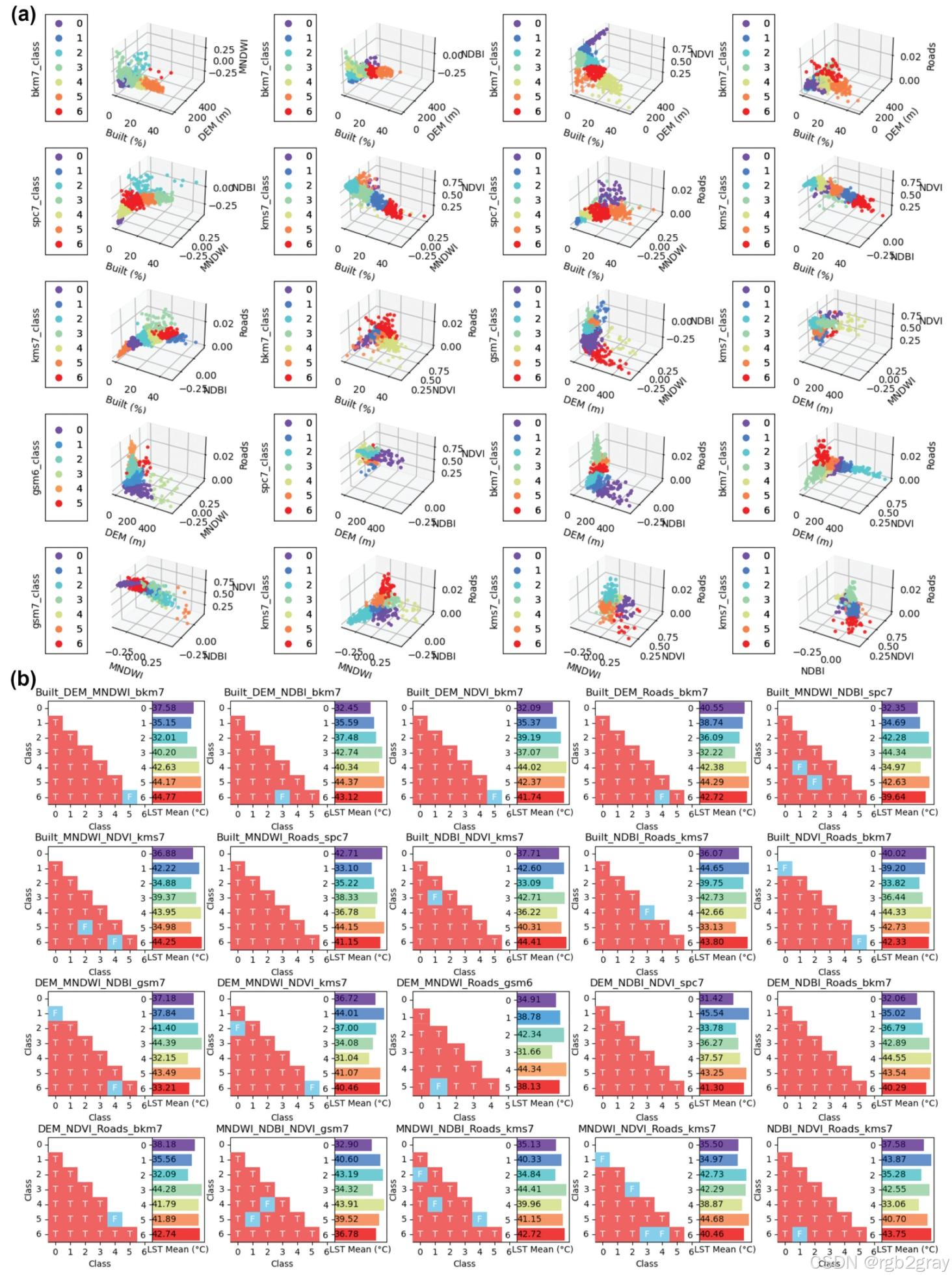
图7 三因子组合最优离散化(a)与风险探测器(b)结果：x/y/z轴为三个因子，不同颜色为聚类分层

关键结果：

1. 最优分层数：仅DEM+MNDWI+Roads为6层，其余均为7层；
2. 最优聚类方法：二分K-means和K-means各7次，谱聚类和GMM各3次；
3. 聚类有效性：能有效捕捉三因子的组合特征（如Built+DEM+NDBI组合中，先按建筑密度分层，再按高程和建筑指数细分）；
4. 风险探测器：层间LST均值差异显著，验证了多因子聚类分层的有效性。

5.2.4 ≥4因子组合（图9）

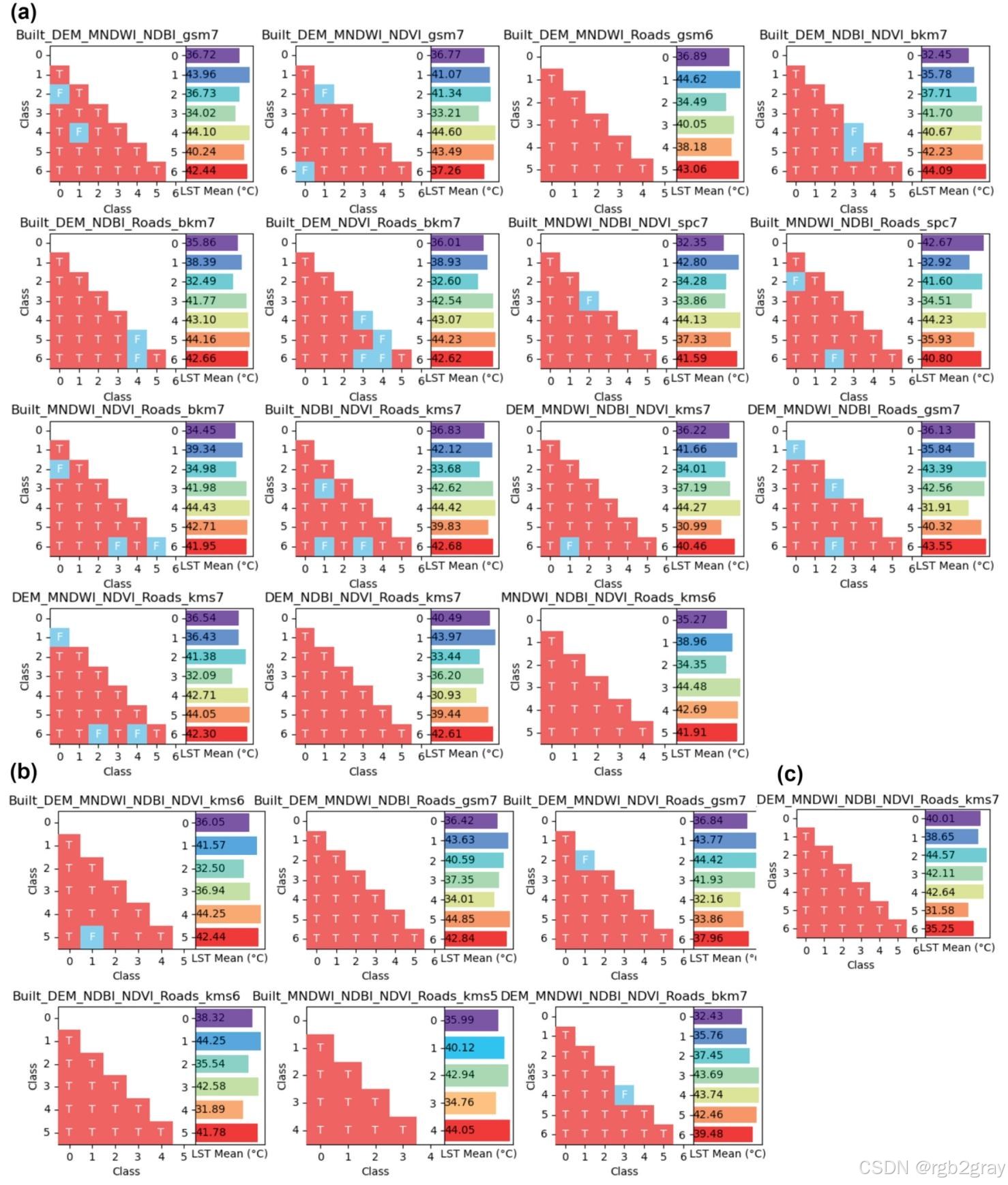
因维度限制无法可视化，但风险探测器结果显示：绝大多数层间LST均值差异显著，说明OMGD的聚类基分层法能有效处理高维因子组合，解决了传统模型的多因子分析难题。

5.3 四大基础探测器结果

基于最优离散化方案，计算因子、生态、交互探测器结果，核心分析单因子、双因子、三因子、≥4因子对LST的解释力差异。

5.3.1 单因子

• 因子探测器（图10a）：NDBI（0.718）、NDVI（0.699）为最主要影响因子，其次为Built（0.612）、DEM（0.544）；
• 生态探测器（图10b）：除NDVI与NDBI外，其余因子的解释力存在显著差异；
• 交互探测器 （图10c）：Built+NDBI（0.786）、MNDWI+NDBI（0.784）、NDBI+Roads（0.779）的交互解释力最强，均为双因子增强。

5.3.2 双因子组合（图11）

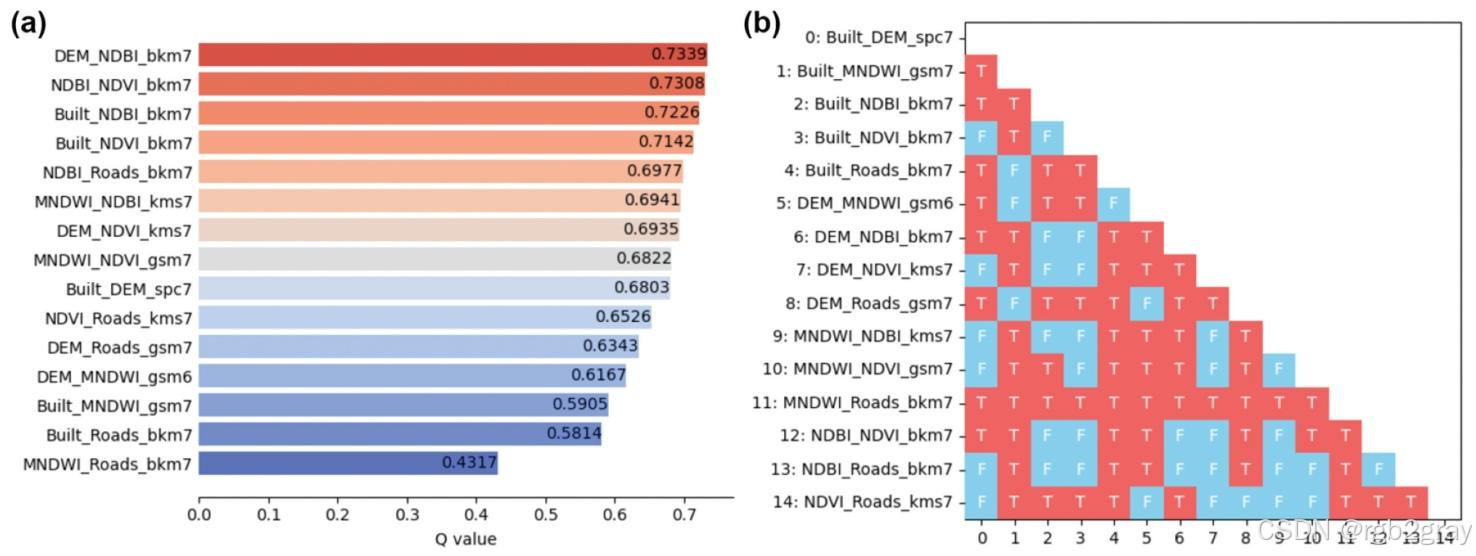
• 因子探测器：双因子组合的q值普遍高于单因子，DEM+NDBI、NDBI+NDVI、Built+NDBI的q值均>0.720，说明NDBI与其他因子的组合能更好地解释LST的SSH；
• 生态探测器：因多数组合共享单因子，仅约50%的组合间解释力存在显著差异。

5.3.3 三因子组合（图12）

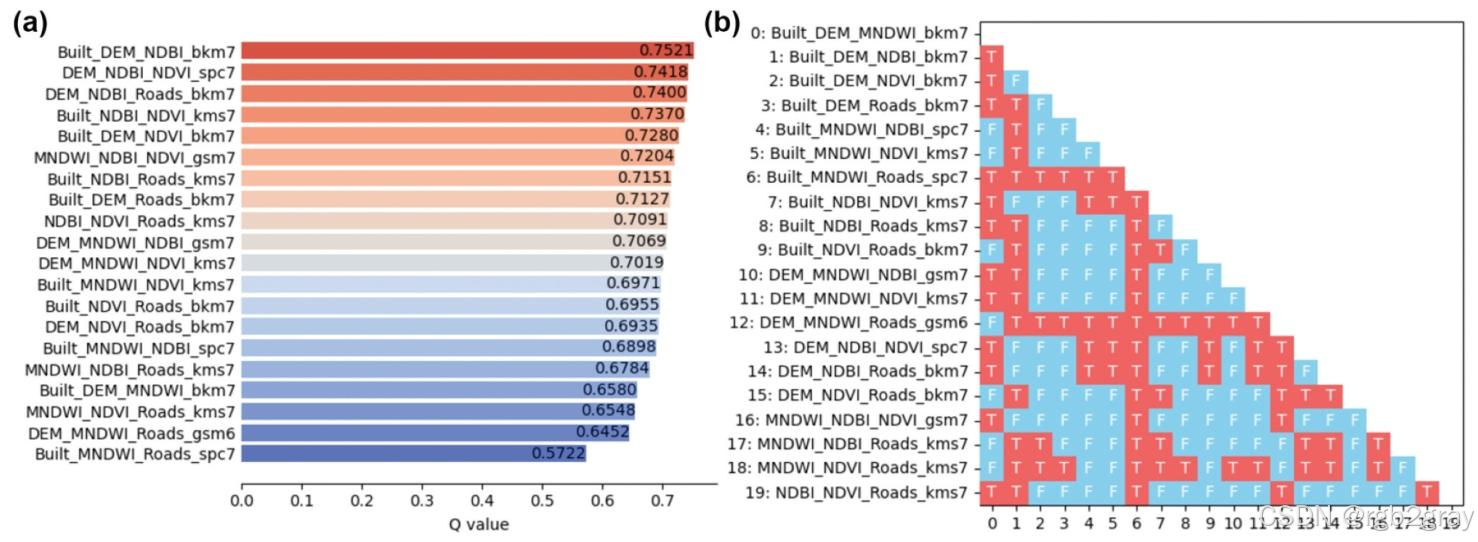
• 因子探测器 ：三因子组合的q值普遍高于单/双因子，Built+DEM+NDBI、DEM+NDBI+NDVI的q值>0.740，为最优解释组合；
• 生态探测器：因多数组合共享核心因子（NDBI），组合间解释力无显著差异。

5.3.4 ≥4因子组合（图13）

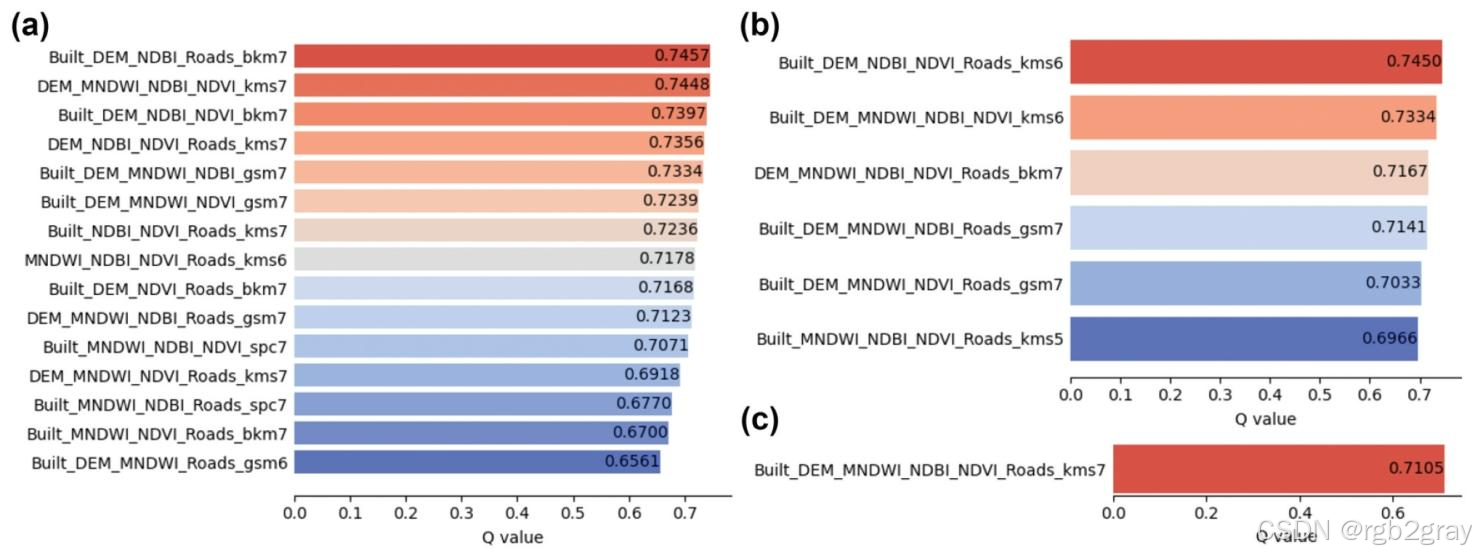
• 因子探测器 ：q值较三因子组合有所下降，原因是分层数（≤7）有限，无法充分捕捉高维因子的组合特征；
• 核心结论 ：三因子组合是解释深圳LST SSH的最优因子组合维度，过多因子会导致信息冗余。

5.4 OMGD与OPGD模型对比

从空间尺度优化 、因子探测器 、双因子探测器vs交互探测器三个维度对比，验证OMGD的优越性。

5.4.1 空间尺度优化对比

• OPGD：仅支持90%分位数的单因子尺度优化；
• OMGD：支持自定义分位数的单/多因子尺度优化；
• 结果：NDVI变化数据中，OPGD最优尺度40km，OMGD 80%分位数40km、60/40%分位数50km；H1N1数据中，OPGD最优尺度100km，OMGD所有分位数均为150km，更贴合地理实际。

5.4.2 因子探测器对比（图16-17+表3）

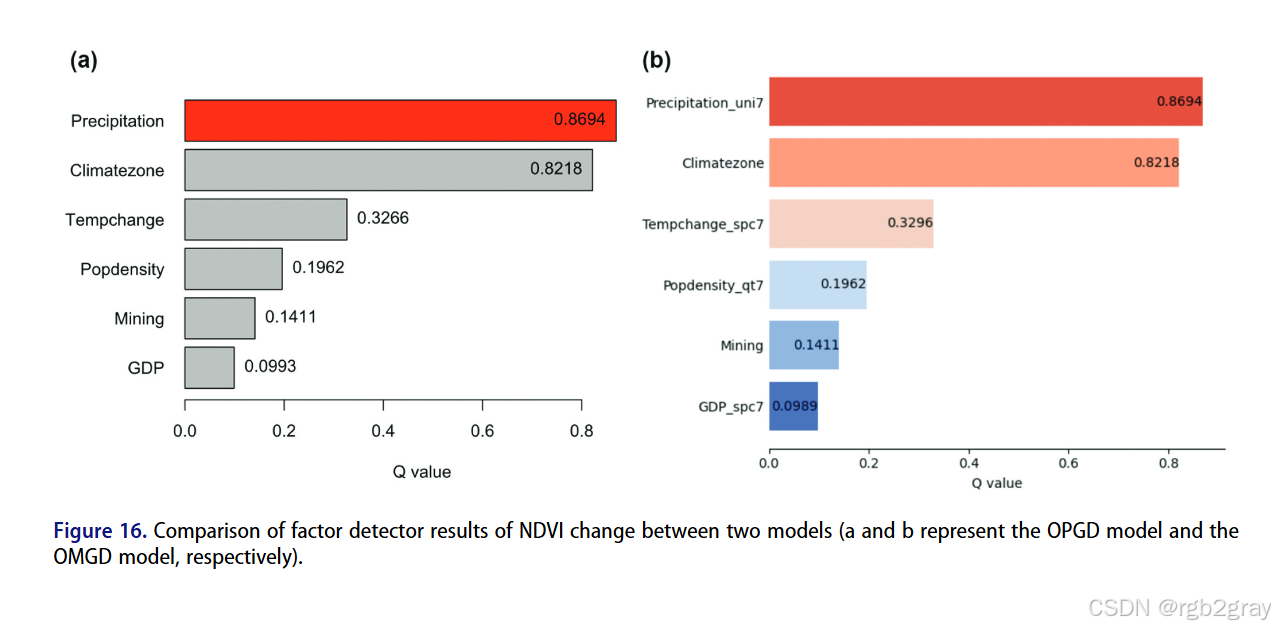
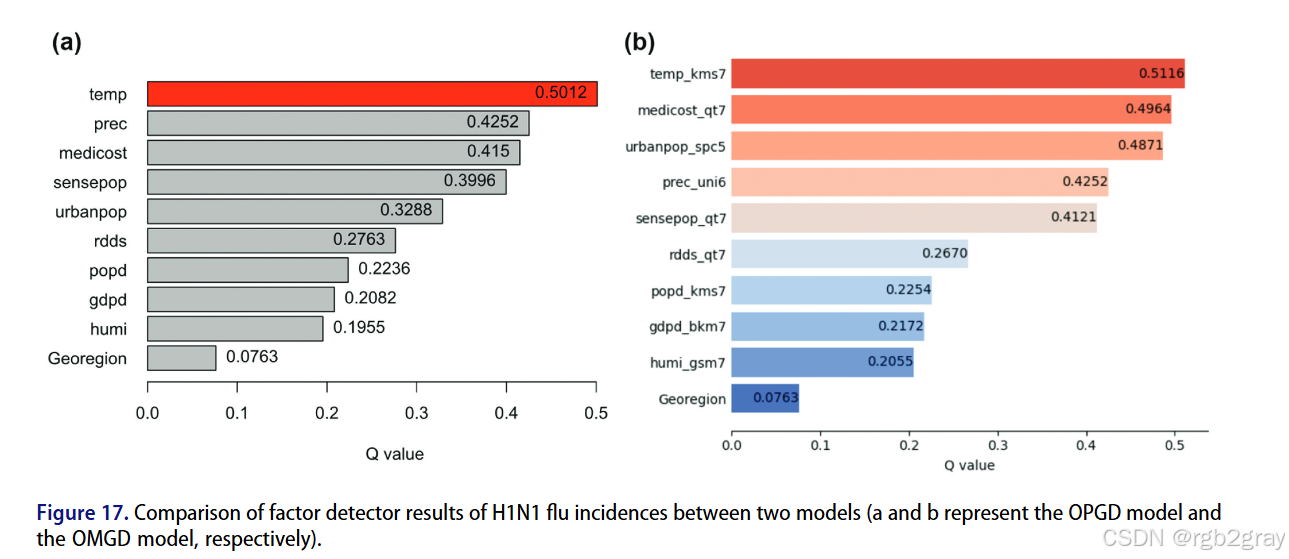
1. NDVI变化数据：两者q值接近，OMGD因新增聚类基分层法，温度变化的q值略有提升；
2. H1N1流感数据：OMGD的q值显著高于OPGD，且影响因子排名变化（医疗成本、城市人口占比的重要性提升），更贴合实际；
3. 模拟数据 （表3）：OMGD在多项式/指数关系的变量中q值更高，说明聚类基分层法比传统单变量分层法更适配复杂的变量关系。

5.4.3 双因子探测器vs交互探测器对比

• 交互探测器：分层数为两个因子分层数的乘积（最大49层），q值更高，但易导致层内样本不足；
• OMGD双因子探测器：聚类基分层法，分层数≤7，q值低于交互探测器，但高于单因子，且层内样本充足，地理意义更明确；
• 核心结论 ：OMGD的多因子探测器在解释力 和样本有效性之间实现了更好的平衡。

六、讨论

研究从分层数与空间尺度的敏感性分析 、OMGD模型的泛化性与可迁移性 、模型优势与局限性三个维度展开讨论，为模型的应用和改进提供参考。

6.1 分层数与空间尺度的敏感性分析

6.1.1 分层数的敏感性（表4）

• 规律：q值随分层数增加总体上升，因分层数越多，层内方差越小；
• 平衡：分层数过多会导致层内样本不足 ，失去地理和统计意义，论文中3~7层是最优区间；
• 结论：OMGD对分层数敏感，需根据研究区样本量合理设置分层数区间。

6.1.2 空间尺度的敏感性（图20-21）

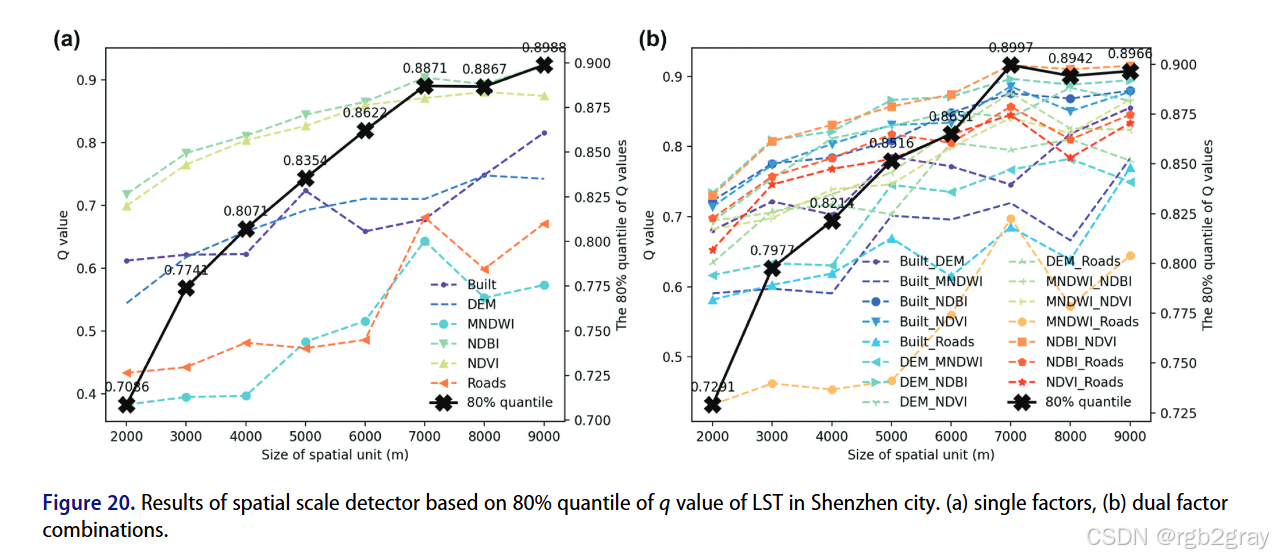
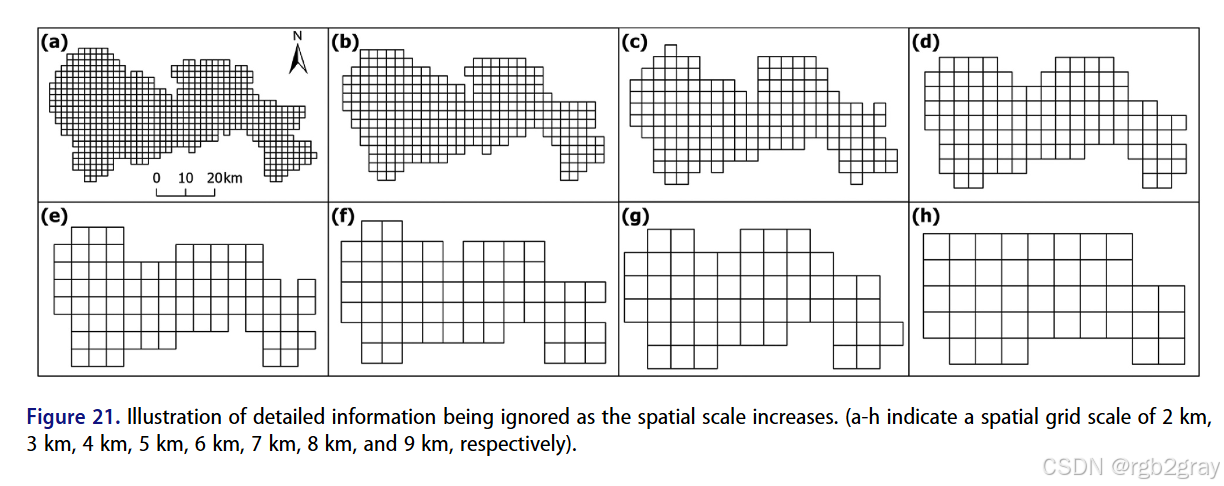
• 规律：q值随空间尺度增大总体上升，因粗粒度网格会平均掉噪声，提升解释力；
• 平衡：尺度过粗会丢失地理细节（如图21，深圳2km网格能捕捉局部热岛，9km网格则完全模糊）；
• 结论：OMGD的尺度探测器能有效平衡解释力 和地理细节，避免尺度选择的主观性。

6.2 OMGD模型的泛化性与可迁移性

基于空间统计三位一体（SST） 框架，通过随机抽样（25%/50%/75%/100%） 验证模型的泛化性，结果如下（表5-6）：

1. 不同抽样比例下，q值保持稳定 ，且均通过显著性检验（p<0.001p<0.001p<0.001）；
2. 影响因子的排名基本不变，说明模型对样本量的鲁棒性强；
3. 模型可迁移至不同研究区、不同因变量（NDVI变化、H1N1流感、城市热环境），泛化性良好。

6.3 OMGD模型的优势与局限性

6.3.1 四大核心优势

1. 多因子处理能力：首次实现≥3因子的自动化最优离散化，解决了传统模型的多因子分析难题；
2. 分层方法丰富：整合5种单变量+5种聚类基分层法，适配不同类型的地理数据；
3. 尺度分析全面：支持单/多因子组合的空间尺度优化，自定义分位数，更贴合地理研究需求；
4. 可视化与开源：提供丰富的可视化函数，模型完全开源，支持二次开发。

6.3.2 三大局限性

1. 量纲处理单一 ：仅采用z-score标准化，未考虑各因子的地理重要性，可能掩盖关键因子的作用；
2. 分层方法仍有缺失：未整合多准则分层法（空间连通性），对需考虑空间邻域的研究适配性不足；
3. 分层数手动设置 ：需人工设置分层数区间，未实现分层数的自动化最优选择，后续需结合算法实现自适应分层。

七、结论

研究提出的最优多元分层地理探测器（OMGD） 模型，通过新增因子离散化优化 和尺度探测器 模块，实现了单/多因子的自动化最优离散化 和单/多因子组合的空间尺度最优选择，大幅提升了地理探测器在SSH分析中的能力。核心结论如下：

1. OMGD能有效提取单因子和多因子组合的核心特征，三因子组合是解释地理现象SSH的最优维度，过多因子会导致信息冗余；
2. 尺度探测器能准确识别单/多因子组合的最优空间尺度，解决了传统模型尺度分析单一的问题，为地理研究的尺度选择提供了客观依据；
3. 与传统OPGD模型相比，OMGD在复杂变量关系 、多因子分析 、尺度自定义上具有显著优势，且模型泛化性强，可迁移至不同研究区和研究主题；
4. 聚类基分层法比传统单变量分层法更适配复杂的地理数据分布，尤其是多项式/指数关系的变量。

7.1 未来研究方向

1. 整合多准则分层法，融入空间连通性约束，提升模型对空间邻域的考虑；
2. 开发自适应分层数算法，实现分层数的自动化最优选择，减少人工干预；
3. 引入因子权重，结合地理知识为不同因子赋予权重，优化多因子组合的离散化效果；
4. 拓展模型的时间维度，实现时空分层异质性的分析，适配时空地理研究需求。

原文：An optimal multivariate-stratification geographical detector model for revealing the impact of multi-factor combinations on the dependent variable