栈与队列基础

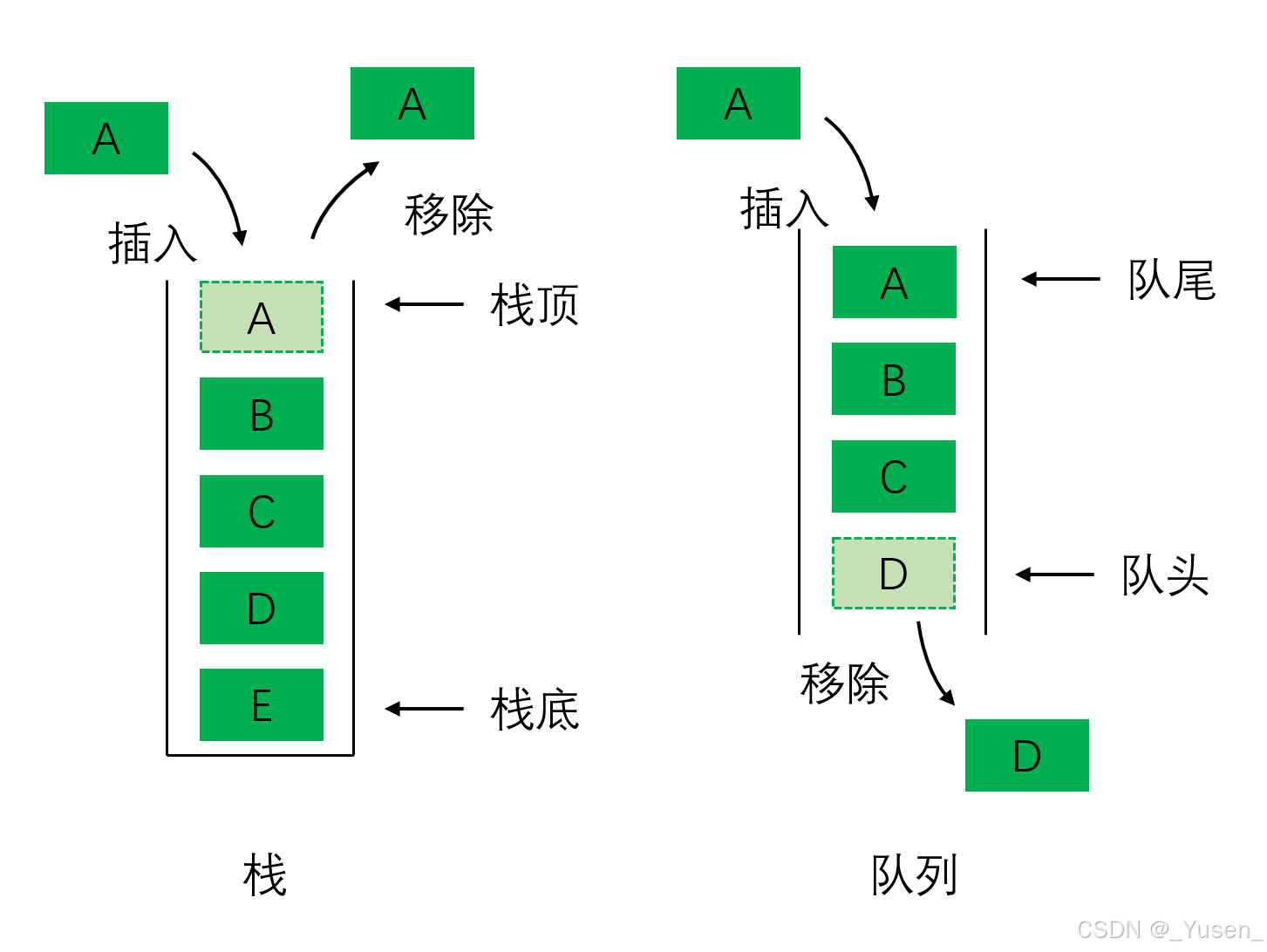
栈的介绍

栈是一种常见的数据结构，

它遵循后进先出（LIFO）的原则，

类似于日常生活中的一叠盘子：

最后放上去的盘子最先被取走。

栈在计算机科学中应用广泛，

例如函数调用、表达式求值和撤销操作等。

下面我将逐步介绍栈的特性、基本操作、实现示例和应用场景。

1. 栈的特性

栈的核心特性是 LIFO，

即元素只能从一端（称为"栈顶"）进行插入和删除操作。

具体来说：

栈顶：栈的顶部位置，所有操作都在这里进行。
栈底：栈的底部位置，元素从这里开始存储。
大小限制：栈可以是固定大小或动态扩展的，取决于实现。

栈的操作时间复杂度通常是常数时间，

例如插入和删除操作的时间复杂度为 $O(1)$ 。

2. 栈的基本操作

栈支持以下基本操作：

push（入栈）：将一个元素添加到栈顶。如果栈已满（在固定大小栈中），可能会导致溢出。
pop（出栈）：从栈顶移除一个元素并返回它。如果栈为空，则称为下溢。
peek（查看栈顶）：返回栈顶元素但不移除它。
isEmpty（判断空）：检查栈是否为空。
size（获取大小）：返回栈中元素的数量。

这些操作的效率很高，

例如在动态数组实现中，

push 和 pop 的平均时间复杂度为 O(1)。

栈的实现示例（C++）

以下是基于数组和基于链表的两种栈实现方式，包含基本操作（压栈、弹栈、查看栈顶等）的完整代码示例。

基于数组的栈实现

cpp 复制代码

#include <iostream>
using namespace std;

#define MAX_SIZE 100

class ArrayStack {
private:
    int data[MAX_SIZE];
    int topIndex;

public:
    ArrayStack() : topIndex(-1) {}

    bool isEmpty() {
        return topIndex == -1;
    }

    bool isFull() {
        return topIndex == MAX_SIZE - 1;
    }

    void push(int value) {
        if (isFull()) {
            cout << "Stack Overflow" << endl;
            return;
        }
        data[++topIndex] = value;
    }

    int pop() {
        if (isEmpty()) {
            cout << "Stack Underflow" << endl;
            return -1;
        }
        return data[topIndex--];
    }

    int peek() {
        if (isEmpty()) {
            cout << "Stack is empty" << endl;
            return -1;
        }
        return data[topIndex];
    }
};

int main() {
    ArrayStack stack;
    stack.push(10);
    stack.push(20);
    cout << stack.peek() << endl; // 20
    stack.pop();
    cout << stack.peek() << endl; // 10
    return 0;
}

基于链表的栈实现

cpp 复制代码

#include <iostream>
using namespace std;

class Node {
public:
    int data;
    Node* next;
    Node(int val) : data(val), next(nullptr) {}
};

class LinkedListStack {
private:
    Node* topNode;

public:
    LinkedListStack() : topNode(nullptr) {}

    bool isEmpty() {
        return topNode == nullptr;
    }

    void push(int value) {
        Node* newNode = new Node(value);
        newNode->next = topNode;
        topNode = newNode;
    }

    int pop() {
        if (isEmpty()) {
            cout << "Stack Underflow" << endl;
            return -1;
        }
        Node* temp = topNode;
        int poppedValue = temp->data;
        topNode = topNode->next;
        delete temp;
        return poppedValue;
    }

    int peek() {
        if (isEmpty()) {
            cout << "Stack is empty" << endl;
            return -1;
        }
        return topNode->data;
    }
};

int main() {
    LinkedListStack stack;
    stack.push(5);
    stack.push(15);
    cout << stack.peek() << endl; // 15
    stack.pop();
    cout << stack.peek() << endl; // 5
    return 0;
}

在这个实现中：

push 方法使用列表的 append 在栈顶添加元素。
pop 方法使用 pop 移除并返回最后一个元素。
所有操作的时间复杂度为 $O(1)$ ，因为列表的末尾操作是高效的。

4. 栈的应用场景

栈在编程和算法中应用广泛：

函数调用栈：
程序执行时，
函数调用和返回使用栈管理局部变量和返回地址。
表达式求值：
在计算器或编译器中使用栈处理括号匹配和运算符优先级，
例如中缀转后缀表达式。
撤销操作：
软件中的撤销功能通过栈存储操作历史。
深度优先搜索（DFS）：
在图或树遍历中，
栈用于管理节点访问顺序。

例如，在表达式求值中，栈可以帮助处理像 $(a + b) \* c$ 这样的表达式，确保正确计算顺序。

总结

栈是一种高效、简单的数据结构，其 LIFO 特性使其在特定场景下非常有用。通过掌握栈的基本操作和实现，可以更好地理解算法设计。

例题：

洛谷B3614 【模板】栈

题目描述

请你实现一个栈（stack），支持如下操作：

push(x)：向栈中加入一个数 x。
pop()：将栈顶弹出。如果此时栈为空则不进行弹出操作，输出 Empty。
query()：输出栈顶元素，如果此时栈为空则输出 Anguei!。
size()：输出此时栈内元素个数。

输入格式

本题单测试点内有多组数据 。

输入第一行是一个整数 T，表示数据组数。对于每组数据，格式如下：

每组数据第一行是一个整数，表示操作的次数 n。

接下来 n 行，每行首先由一个字符串，为 push，pop，query 和 size 之一。若为 push，则其后有一个整数 x，表示要被加入的数，x 和字符串之间用空格隔开；若不是 push，则本行没有其它内容。

输出格式

对于每组数据，按照「题目描述」中的要求依次输出。每次输出占一行。

输入输出样例

输入 #1

复制代码

2
5
push 2
query
size
pop
query
3
pop
query
size

输出 #1

复制代码

2
1
Anguei!
Empty
Anguei!
0

说明/提示

样例 1 解释

对于第二组数据，始终为空，所以 pop 和 query 均需要输出对应字符串。栈的 size 为 0。

数据规模与约定

对于全部的测试点，保证 1≤T,n≤106，且单个测试点内的 n 之和不超过 106，即 ∑n≤106。保证 0≤x<264。

提示

请注意大量数据读入对程序效率造成的影响。
因为一开始数据造错了，请注意输出的 Empty 不含叹号，Anguei! 含有叹号。

题目分析

题目要求实现一个栈结构，支持四种操作：push、pop、query和size。每组数据包含多个操作，需要根据操作类型输出相应的结果。栈为空时，pop操作输出Empty，query操作输出Anguei!，size操作输出当前栈的大小。

输入输出格式

输入的第一行是测试用例的数量T。每个测试用例的第一行是操作的数量n，接下来的n行是具体的操作。对于push操作，后面跟着一个整数x；其他操作没有额外参数。

输出需要根据操作类型和栈的状态输出相应的结果。

解决思路

栈的实现：使用数组或链表实现栈结构，数组的实现更简单且高效。
操作处理：根据输入的操作类型执行相应的栈操作，并输出结果。
高效输入输出 ：由于数据量较大（最多10^6次操作），需要使用快速的输入输出方法，如scanf和printf，避免使用cin和cout。

代码实现

cpp 复制代码

#include<bits/stdc++.h>
using namespace std;
#define MAX_N 1000000

int stack[MAX_N];
int top = 0;

void push(int x) {
    stack[top++] = x;
}

void pop() {
    if (top == 0) {
        printf("Empty\n");
    } else {
        top--;
    }
}

void query() {
    if (top == 0) {
        printf("Anguei!\n");
    } else {
        printf("%d\n", stack[top - 1]);
    }
}

void size() {
    printf("%d\n", top);
}

int main() {
    int T;
    scanf("%d", &T);
    while (T--) {
        int n;
        scanf("%d", &n);
        top = 0;
        char op[10];
        int x;
        while (n--) {
            scanf("%s", op);
            if (strcmp(op, "push") == 0) {
                scanf("%d", &x);
                push(x);
            } else if (strcmp(op, "pop") == 0) {
                pop();
            } else if (strcmp(op, "query") == 0) {
                query();
            } else if (strcmp(op, "size") == 0) {
                size();
            }
        }
    }
    return 0;
}
 

?

cpp 复制代码

#include<bits/stdc++.h>
using namespace std;
unsbigned long long a[100005];
unsbigned long long t,n;
unsbigned long long k=1;
string s;
int main(){
	cin>>t;
	for(int i=1;i<=t;i++){
		cin>>n;
		for(int j=1;j<=n;j++){
			cin>>s;
			unsbigned long long x;
			if(s=="push"){
				cin>>x;
				a[k]=x;
				k++;
			}
			if(s=="pop"){
				if(k>1){
					a[k-1]=0;
					k--;
				}
				else{
					printf("Empty\n") 
				}
			}
			if(s=="query"){
				if(k>1){
					cout<<a[k-1];
				}
				else printf("Empty\n");
			}
			if(s=="size"){
				cout<<k-1<<'\n';
			}
		}
		memset(a,0,sizeof(a));
		k=1;
	}
	return 0;
}


给个三连^_+求求了

队列的基本概念

队列是一种遵循**先进先出（FIFO, First In First Out）**原则的线性数据结构。元素的插入（入队）发生在队列的尾部，而元素的删除（出队）发生在队列的头部。队列的典型操作包括：

入队（Enqueue）：向队列尾部添加元素。
出队（Dequeue）：从队列头部移除元素并返回。
查看队头（Peek/Front）：获取队头元素但不移除。
判空（isEmpty）：检查队列是否为空。

队列的实现方式

队列可以通过数组或链表实现，两种方式各有优缺点：

基于数组的实现

需要预先分配固定大小的空间，可能发生溢出。
使用循环数组优化空间利用率（避免频繁移动元素）。示例代码（循环队列）：

示例代码（循环队列）：

循环队列类定义

cpp 复制代码

class CircularQueue {
private:
    int *arr;       // 存储队列元素的数组
    int front;      // 队首指针
    int rear;       // 队尾指针
    int capacity;   // 队列容量
    int size;       // 当前元素数量

public:
    // 构造函数
    CircularQueue(int k) {
        capacity = k;
        arr = new int[k];
        front = 0;
        rear = -1;
        size = 0;
    }

    // 析构函数
    ~CircularQueue() {
        delete[] arr;
    }

入队操作

cpp 复制代码

    bool enQueue(int value) {
        if (isFull()) {
            return false; // 队列已满
        }
        rear = (rear + 1) % capacity; // 循环处理队尾指针
        arr[rear] = value;
        size++;
        return true;
    }

出队操作

cpp 复制代码

    bool deQueue() {
        if (isEmpty()) {
            return false; // 队列为空
        }
        front = (front + 1) % capacity; // 循环处理队首指针
        size--;
        return true;
    }

获取队首元素

cpp 复制代码

    int Front() {
        if (isEmpty()) {
            return -1; // 队列为空
        }
        return arr[front];
    }

获取队尾元素

cpp 复制代码

    int Rear() {
        if (isEmpty()) {
            return -1; // 队列为空
        }
        return arr[rear];
    }

判断队列是否为空

cpp 复制代码

    bool isEmpty() {
        return size == 0;
    }

判断队列是否已满

cpp 复制代码

    bool isFull() {
        return size == capacity;
    }
};

例题洛谷B3616 【模板】队列

题目描述

请你实现一个队列（queue），支持如下操作：

push(x)：向队列中加入一个数 x。
pop()：将队首弹出。如果此时队列为空，则不进行弹出操作，并输出 ERR_CANNOT_POP。
query()：输出队首元素。如果此时队列为空，则输出 ERR_CANNOT_QUERY。
size()：输出此时队列内元素个数。

输入格式

第一行，一个整数 n，表示操作的次数。

接下来 n 行，每行表示一个操作。格式如下：

1 x，表示将元素 x 加入队列。
2，表示将队首弹出队列。
3，表示查询队首。
4，表示查询队列内元素个数。

输出格式

输出若干行，对于每个操作，按「题目描述」输出结果。

每条输出之间应当用空行隔开。

输入输出样例

输入 #1

复制代码

输出 #1

复制代码

2
1
2
233
0
ERR_CANNOT_QUERY
ERR_CANNOT_POP
144

说明/提示

样例解释

首先插入 2，队首为 2、队列内元素个数为 1。

插入 233，此时队首为 2。

弹出队首，此时队首为 233。

弹出队首，此时队首为空。

再次尝试弹出队首，由于队列已经为空，此时无法弹出。

插入 144，此时队首为 144。

数据规模与约定

对于 100% 的测试数据，满足 n≤10000，且被插入队列的所有元素值是 [1,1000000] 以内的正整数。

队列实现思路

队列是一种先进先出（FIFO）的数据结构，可以通过数组或链表实现。以下是一个基于数组的队列实现方案：

使用数组存储队列元素，并维护队首和队尾指针
初始化时设置队首(front)和队尾(rear)指针为0
每次push操作在队尾添加元素，并移动rear指针
每次pop操作从队首移除元素，并移动front指针

关键操作实现

push(x)操作

将元素x放入rear指针位置
rear指针后移一位
时间复杂度：O(1)

pop()操作

检查队列是否为空(front == rear)
不为空则移动front指针
时间复杂度：O(1)

query()操作

检查队列是否为空
不为空则返回front指针位置的元素
时间复杂度：O(1)

size()操作

返回rear - front的差值
时间复杂度：O(1)

边界条件处理

空队列判断：front == rear
弹出空队列：输出ERR_CANNOT_POP
查询空队列：输出ERR_CANNOT_QUERY

代码实现

cpp 复制代码

#include <iostream>
using namespace std;

const int MAX_SIZE = 10000;
int queue[MAX_SIZE];
int front = 0, rear = 0;

void push(int x) {
    if (rear < MAX_SIZE) {
        queue[rear++] = x;
    }
}

void pop() {
    if (front == rear) {
        cout << "ERR_CANNOT_POP" << endl;
    } else {
        front++;
    }
}

void query() {
    if (front == rear) {
        cout << "ERR_CANNOT_QUERY" << endl;
    } else {
        cout << queue[front] << endl;
    }
}

void size() {
    cout << (rear - front) << endl;
}

int main() {
    int n, op, x;
    cin >> n;
    while (n--) {
        cin >> op;
        switch (op) {
            case 1:
                cin >> x;
                push(x);
                break;
            case 2:
                pop();
                break;
            case 3:
                query();
                break;
            case 4:
                size();
                break;
        }
        cout << endl; // 每个操作后输出空行
    }
    return 0;
}

给个三连吧！！！

免费的赞也行啊+-+

共6666个字......

栈与队列基础

栈的介绍

1. 栈的特性

2. 栈的基本操作

栈的实现示例（C++）

基于数组的栈实现

基于链表的栈实现

4. 栈的应用场景

总结

例题：

洛谷B3614 【模板】栈

题目描述

输入格式

输出格式

输入输出样例

说明/提示

样例 1 解释

数据规模与约定

提示

题目分析

输入输出格式

解决思路

代码实现

队列的基本概念

队列的实现方式

示例代码（循环队列）：

循环队列类定义

入队操作

出队操作

获取队首元素

获取队尾元素

判断队列是否为空

判断队列是否已满

例题 洛谷B3616 【模板】队列

题目描述

输入格式

输出格式

输入输出样例

说明/提示

样例解释

数据规模与约定

队列实现思路

关键操作实现

push(x)操作

pop()操作

query()操作

size()操作

边界条件处理

代码实现

例题洛谷B3616 【模板】队列