1. 标量方程对向量的求导
对向量求导前需要明确使用哪种布局形式,主要分为分母布局和分子布局。
1.1 分母布局
定义y→=[y1..ym]m×1\overrightarrow{y}= \begin{bmatrix} y_1\\ .\\ .\\ y_m\\ \end{bmatrix}{m\times1}y = y1..ym m×1,f(y→)f(\overrightarrow{y})f(y )为标量,则:
∂f(y→)∂y→=[∂f(y→)∂y1..∂f(y→)∂ym]m×1\frac{\partial f(\overrightarrow{y})}{\partial \overrightarrow{y}}= \begin{bmatrix} \frac{\partial f(\overrightarrow{y})}{\partial y_1}\\ .\\ .\\ \frac{\partial f(\overrightarrow{y})}{\partial y_m} \end{bmatrix}{m\times1}∂y ∂f(y )= ∂y1∂f(y )..∂ym∂f(y ) m×1
可以发现求导的结果也是一个向量,且该向量的行数与分母的行数相同(都为m),这种布局称为分母布局。
1.2 分子布局
定义y→=[y1..ym]1×n\overrightarrow{y}= \begin{bmatrix} y_1&.&.&y_m \end{bmatrix}_{1\times n}y =[y1..ym]1×n,f(y→)f(\overrightarrow{y})f(y )为标量,则
∂f(y→)∂y→=[∂f(y→)∂y1..∂f(y→)∂ym]1×n\frac{\partial f(\overrightarrow{y})}{\partial \overrightarrow{y}}= \begin{bmatrix} \frac{\partial f(\overrightarrow{y})}{\partial y_1}&.&.&\frac{\partial f(\overrightarrow{y})}{\partial y_m} \end{bmatrix}_{1\times n}∂y ∂f(y )=[∂y1∂f(y )..∂ym∂f(y )]1×n
可以发现求导的结果也是一个向量,且该向量的行数与分子的行数相同(都为1),这种布局称为分子布局。
2. 向量方程对向量的求导
2.1 定义
以下所有推导都采用分母布局。
定义y→=[y1..ym]m×1\overrightarrow{y}= \begin{bmatrix} y_1\\ .\\ .\\ y_m\\ \end{bmatrix}{m\times1}y = y1..ym m×1,f(y→)=[f1(y→)..fn(y→)]n×1f(\overrightarrow{y})= \begin{bmatrix} f_1(\overrightarrow{y})\\ .\\ .\\ f_n(\overrightarrow{y})\\ \end{bmatrix}{n\times1}f(y )= f1(y )..fn(y ) n×1也为向量,则
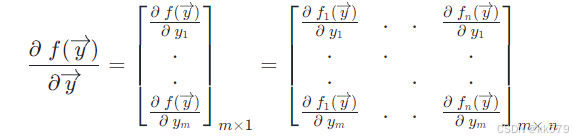
因为是采用分母布局,所以要严格保证求导后的向量的行数要跟分母相同(都为m),因此在对向量f(y→)f(\overrightarrow{y})f(y )进行展开时展开成行的形式。
举个例子,假设y→=[y1y2y3]3×1\overrightarrow{y}= \begin{bmatrix} y_1\\ y_2\\ y_3\\ \end{bmatrix}{3\times1}y = y1y2y3 3×1,f(y→)=[y12+y22y22+2y3]2×1f(\overrightarrow{y})= \begin{bmatrix} y_1^2+y_2^2\\ y_2^2+2y_3\\ \end{bmatrix}{2\times1}f(y )=[y12+y22y22+2y3]2×1,则
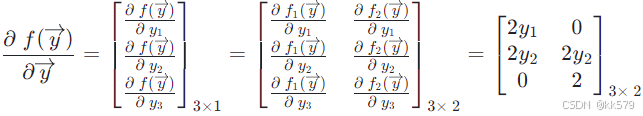
2.2 两个常用的特例
1️⃣
若y→=[y1..ym]m×1\overrightarrow{y}= \begin{bmatrix} y_1\\ .\\ .\\ y_m\\ \end{bmatrix}{m\times1}y = y1..ym m×1,A=[a11..a1m......a1m..amm]m×mA= \begin{bmatrix} a{11}&.&.&a_{1m}\\ .&.&&.\\ .&&.&.\\ a_{1m}&.&.&a_{mm} \end{bmatrix}_{m\times m}A= a11..a1m......a1m..amm m×m,则有
∂Ay→∂y→=AT\frac{\partial A\overrightarrow{y}}{\partial \overrightarrow{y}} = A^T∂y ∂Ay =AT
2️⃣
若y→=[y1..ym]m×1\overrightarrow{y}= \begin{bmatrix} y_1\\ .\\ .\\ y_m\\ \end{bmatrix}{m\times1}y = y1..ym m×1,,,A=[a11..a1m......a1m..amm]m×mA= \begin{bmatrix} a{11}&.&.&a_{1m}\\ .&.&&.\\ .&&.&.\\ a_{1m}&.&.&a_{mm} \end{bmatrix}_{m\times m}A= a11..a1m......a1m..amm m×m,则有
∂y→TAy→∂y→=Ay→+ATy→\frac{\partial \overrightarrow{y}^TA\overrightarrow{y}}{\partial \overrightarrow{y}} = A\overrightarrow{y}+A^T\overrightarrow{y} ∂y ∂y TAy =Ay +ATy (重要)