写在前面
笔者是大二acm选手，参加今年寒假牛客训练赛，当前已经是打完六场，这一场补第六场的题，其他场的补题可以在我的主页里找到
这一场主要补两个题，一个是函数分析，一个是组合数学
可能是因为最后一场打的人不多了，这场五题就能排到六七百名左右
注：比赛题目来自于牛客竞赛，题解参考牛客竞赛官方题解
比赛链接：https://ac.nowcoder.com/acm/contest/120566#rank/%22page%22%3A21
A
题面
注：题目
题意解释
给定n个三角尺和w的打磨额度，打磨额度可以用在打磨这些三角尺的一条直角边，但是单次打磨必须是整数。问最后将打磨额度用光或者将全部三角尺打磨成直线之后，这n把三角尺的斜边长度之和最小是多少
思路
其实这道题的本质就是计算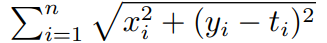
的最小值
对斜边计算公式的y求导，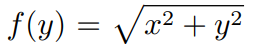
，可以得到的是随着y的减小，y单次减少1时f(y)减少量越来越小
所以在x不变的情况下，y越大，打磨的价值更大
因此我们可以比较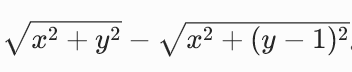
，将其从大到小排序，然后每次打磨y的一个长度
可以使用堆来进行时间复杂度优化
代码
cpp
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
double fun(ll x,ll y)
{
return sqrt(x*x+y*y);
}
void solve()
{
ll n,w;
cin>>n>>w;
priority_queue<pair<double,pair<ll,ll>>>vec;
while(n--)
{
ll x,y;
cin>>x>>y;
double p=sqrt(x*x+y*y)-sqrt(x*x+(y-1)*(y-1));
vec.push({p,{y,x}});
}
while(w--)
{
ll top_y=vec.top().second.first;
ll top_x=vec.top().second.second;
double p=sqrt(top_x*top_x+(top_y-1)*(top_y-1))-sqrt(top_x*top_x+(top_y-2)*(top_y-2));
vec.pop();
if(top_y>=1) vec.push({p,{top_y-1,top_x}});
else
{
vec.push({(double)top_x,{0,top_x}});
break;
}
}
double ans=0;
while(!vec.empty())
{
ll top_y=vec.top().second.first;
ll top_x=vec.top().second.second;
vec.pop();
ans+=fun(top_x,top_y);
}
cout<<fixed<<setprecision(15)<<ans<<endl;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
ll t=1;
//cin>>t;
while(t--)
{
solve();
}
return 0;
}B
题面
题意解释
编号1~n的球放在两个盒子里，每对相邻编号彩球之间都有一条连线，连线可以漏在外面
已知有t条漏在外面的线，问有多少种符合条件的放法
思路
假设这些球是1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
如果相邻的球在一个箱子里，那他内部的排列根本不重要
如果相邻的球不在一个箱子里，就说明这个地方出现了一个分割
所以有几根线就说明有几个分割
举个例子：
一共有四根线，说明在1~n里有4个分割
可能是1 2 3 4 分割 5 6 7 8 9 分割 10 11 12 13 14 15 16 分割 17 18 19 20 分割 21 22 23 24 25 26
就说明4和5、9和10、16和17、20和21放的箱子不是同一个，但是有相邻的球都有线这一条件的限制，1 2 3 4必然在同一个箱子，5 6 7 8 9也必然在同一个箱子，其他同理
也可能是1 2 分割 3 4 5 6 7 8 9 分割 10 11 12 13 14 分割 15 16 17 18 分割 19 20 21 22 23 24 25 26
所以这个问题就转换成了找分割的位置
这里还有一个限制条件，就是左盒球的个数是x
这个条件限制了能插的位置个数，最后答案就是能插的个数中插入t个隔板的情况种数
t分奇偶，当t为奇数时，切出偶数段，这时切出的段数两个箱子可以平分，当t为偶数时，切出奇数段，这时切出的段数有一个箱子会多一段
当t为奇数，段数是偶数时，排列种数就是把x个数放进(t+1)/2段中，相当于(t+1)/2-1插进x-1个槽里
当t为偶数，段数是奇数时，排列种数就是把x个数放进t/2段中或t/2+1段中，计算方法同上，这种两种结果加起来就是答案
计算组合数的时候不能用卢卡斯定理，会超时
代码
cpp
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e6+10, MOD=998244353;
ll fact[N],infact[N];
ll qmi(ll a,ll k,ll p)
{
ll res=1;
while(k)
{
if(k&1) res=res*a%p;
a=a*a%p;
k>>=1;
}
return res;
}
void init()
{
fact[0]=infact[0]=1;
for(ll i=1;i<N;i++)
{
fact[i]=fact[i-1]*i%MOD;
infact[i]=infact[i-1]*qmi(i,MOD-2,MOD)%MOD;
}
}
ll C(ll a, ll b)
{
if(b < 0 || b > a) return 0;
return fact[a] * infact[b] % MOD * infact[a - b] % MOD;
}
void solve()
{
ll n,x,t;
cin>>n>>x>>t;
if(t==0)
{
if(x==0||x==n) cout<<1<<endl;
else cout<<0<<endl;
return;
}
if(t%2!=0)
{
ll q=(t+1)/2;
cout<<2*C(x-1,q-1)*C(n-x-1,q-1)%MOD<<endl;
}
else
{
ll q=t/2;
ll ans=0;
ll case1 = C(x-1, q ) * C(n-x-1, q-1) % MOD;
ll case2 = C(x-1, q-1) * C(n-x-1, q) % MOD;
ans = (case1 + case2) % MOD;
cout<<ans<<endl;
}
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
init();
ll t=1;
cin>>t;
while(t--)
{
solve();
}
return 0;
}篇末总结
本场的B确实比较简单，赛时大概率能开出来，只不过因为榜歪了，再加上我赛时太懒惰，A因为会错意wa了几发，心灰意冷就不做了
2026年牛客寒假训练赛算是补完了，而且今天总榜也出了，我是排在两千名，算二等奖里的下等马
后续继续更新Java学习
祝大家新年快乐，在新的一年代码全跑通，acm同行都能拿牌子，找工作的都能拿到好offer