斯坦福大学 | CS336 | 从零开始构建语言模型 | Spring 2025 | 笔记 | Assignment 2: FlashAttention-2

目录

• • 前言
  • [1. Optimizing Attention with FlashAttention-2](#1. Optimizing Attention with FlashAttention-2)
  • • [1.1 Benchmarking PyTorch Attention](#1.1 Benchmarking PyTorch Attention)
    • • [Problem (pytorch_attention): 2 points](#Problem (pytorch_attention): 2 points)
  • [2. Benchmarking JIT-Compiled Attention](#2. Benchmarking JIT-Compiled Attention)
  • • • [Problem (torch_compile): 2 points](#Problem (torch_compile): 2 points)
    • [2.1 Example - Weighted Sum](#2.1 Example - Weighted Sum)
    • [2.2 FlashAttention-2 Forward Pass](#2.2 FlashAttention-2 Forward Pass)
    • • [Problem (flash_forward): 15 points](#Problem (flash_forward): 15 points)
      • [Problem (flash_backward): 5 points](#Problem (flash_backward): 5 points)
      • [Problem (flash_benchmarking): 5 points](#Problem (flash_benchmarking): 5 points)
    • [2.3 FlashAttention-2 Leaderboard](#2.3 FlashAttention-2 Leaderboard)
    • [2.4 OPTIONAL: Triton backward pass](#2.4 OPTIONAL: Triton backward pass)
  • 结语
  • 参考

前言

本篇文章记录 CS336 作业 Assignment 2: Systems 中的 FlashAttention-2 作业要求，仅供自己参考😄

Assignment 2 ：https://github.com/stanford-cs336/assignment2-systems

reference ：https://chatgpt.com/

1. Optimizing Attention with FlashAttention-2

以下内容均翻译自 cs336_spring2025_assignment2_systems.pdf，请大家查看原文档获取更详细的内容

1.1 Benchmarking PyTorch Attention

你的性能分析结果很可能已经表明，在注意力层中，无论是在 内存使用 还是 计算开销 方面，都存在明显的优化空间。从宏观上看，注意力计算由一次矩阵乘法、一次 softmax 操作以及随后的一次矩阵乘法组成：

Attention ( Q , K , V ) = s o f t m a x ( m a s k ( Q ⊤ K d k ) ) V (1) \text{Attention}(Q, K, V) = \mathrm{softmax}\left(\mathrm{mask}\left(\frac{Q^\top K}{\sqrt{d_k}}\right)\right) V \tag{1} Attention(Q,K,V)=softmax(mask(dk Q⊤K))V(1)

朴素的注意力实现需要为每一个 batch / head 元素保存形状为 seq_len × seq_len \text{seq\_len}\times \text{seq\_len} seq_len×seq_len 的注意力得分矩阵，随着序列长度的增加，这个矩阵会迅速变得非常大，从而在处理长输入或长输出任务时极易导致 显存溢出（out-of-memory）错误

接下来，我们将按照 FlashAttention-2 论文中的方法实现一个注意力计算 Kernel，该方法以 分块（tile） 的方式计算注意力，从而避免显式构造 seq_len × seq_len \text{seq\_len}\times \text{seq\_len} seq_len×seq_len 的注意力得分矩阵，使模型能够扩展到 更长的序列长度

Problem (pytorch_attention): 2 points

(a) 在不同规模下对你的注意力实现进行基准测试，请编写一个脚本，完成以下工作：

1. 将 batch size 固定为 8 ，并且 不使用多头注意力（即去掉 head 这一维度）

2. 对以下参数组合进行遍历（笛卡尔积）：

• head 的嵌入维度 d model ∈ [ 16 , 32 , 64 , 128 ] d_{\text{model}}\in [16, 32, 64, 128] dmodel∈[16,32,64,128]
• 序列长度 ∈ [ 256 , 1024 , 4096 , 8192 , 16384 ] \in [256,1024,4096,8192,16384] ∈[256,1024,4096,8192,16384]

3. 为对应尺寸生成随机输入 Q , K , V Q,K,V Q,K,V

4. 使用这些输入对注意力模块进行 100 次前向传播 并计时

5. 在反向传播开始之前，测量当前的显存使用情况，并对 100 次反向传播 进行计时

6. 确保在正式计时前进行 warm-up ，并且在每一次前向 / 反向传播之前调用 torch.cuda.synchronize()

请报告在这些配置下得到的运行时间（或是否发生了显存溢出错误），在哪些规模下你会遇到 out-of-memory（OOM） 错误？

请对你发现的 最小一个发生 OOM 的配置 ，对注意力模块的显存使用进行理论分析（你可以使用 Assignment 1 中给出的 Transformer 显存占用公式）。反向传播所需的显存节省量会如何随序列长度变化？如果要 彻底消除这部分显存开销，你会采取什么方法？

Deliverable：一张包含运行时间的表格；你对注意力显存使用的推导计算以及一段 1-2 段的文字分析说明。

2. Benchmarking JIT-Compiled Attention

以下内容均翻译自 cs336_spring2025_assignment2_systems.pdf，请大家查看原文档获取更详细的内容

自 PyTorch 2.0 版本起，PyTorch 还提供了一个强大的 即时编译器（Just-In-Time Compiler） ，它会自动尝试对 PyTorch 函数应用多种优化，入门介绍可参考：https://docs.pytorch.org/tutorials/intermediate/torch_compile_tutorial.html

具体来说，该编译器会通过 动态分析计算图 ，自动生成 融合后的 Triton kernel，使用 PyTorch 编译器的接口非常简单，例如，如果我们希望只对模型中的某一层应用编译，可以这样做：

layer = SomePyTorchModule(...)
compiled_layer = torch.compile(layer)

此时，compiled_layer 在功能上与原始的 layer 完全一致（例如，仍然支持前向和反向传播），我们也可以直接对整个 PyTorch 模型使用 torch.compile(model)，甚至可以对一个调用 PyTorch 运算的 Python 函数进行编译

在我们之前观察到的 序列长度扩展行为 背景下，为了支持更长序列，我们仍然需要显著的性能改进，即便使用了 torch.compile，当前实现方式在长序列情况下仍然存在 非常糟糕的内存访问模式

因此，接下来我们将编写一个 FlashAttention-2 的 Triton 实现 ，以便对 内存访问方式 以及 计算调度时机 拥有更精细的控制

Problem (torch_compile): 2 points

(a) 扩展你的 attention 基准测试脚本，使其包含 PyTorch attention 实现的编译版本 ，并在与上面 pytorch_attention 问题相同的配置下，将其性能与 未编译版本 进行对比

Deliverable ：一张表格，对比编译版 attention 模块与 pytorch_attention 问题中未编译版本在前向和反向传播上的耗时。

(b) 接下来，在你的 端到端基准测试脚本 中，对 整个 Transformer 模型 进行编译。前向传播的性能发生了怎样的变化？前向 + 反向传播以及优化器 step 的组合性能又如何变化？

Deliverable：一张表格，对比原始（vanilla）Transformer 模型与编译后的 Transformer 模型的性能。

2.1 Example - Weighted Sum

为了介绍你在 Triton 中需要掌握的知识以及 Triton 如何与 PyTorch 协同合作，我们将通过一个 加权求和（weight sum） 操作的示例 kernel 来进行讲解。如果你希望进一步系统性地学习 Triton，可以参考 Triton 官方教程 （Triton's tutorials），需要注意的是，这些教程并未使用较新的、更加便捷的 block pointer 抽象，而我们将在下面的内容中对这一抽象进行详细讲解

给定一个输入矩阵 X X X，我们将其每个元素与一个 按列定义的权重向量 w w w 相乘，然后对每一行求和，从而得到矩阵 X X X 与向量 w w w 的矩阵-向量乘积结果，我们将首先分析这一操作的 前向计算过程 ，随后再为其实现 反向传播 对应的 Triton kernel

Forward pass

该 kernel 的前向计算本质上就是下面这个 带广播的内积运算：

def weighted_sum(x, weight):
    # Here, assume that x has n-dim shape [..., D], and weight has 1D shape [D]
    return (weight * x).sum(axis=-1)

在编写 Triton kernel 时，我们会让 每一个程序实例（program instance） （这些实例可以并行执行）负责计算输入张量 x x x 中的 一小块行（tile of rows） 的加权求和，并将对应的标量结果写入输出张量

在 Triton 中，一个程序实例对应的是一个 线程块（thread block） ，该线程块中的所有线程都运行相同的程序，而这些线程块可以在 GPU 上并行执行。与 PyTorch 中直接将张量作为函数参数不同，Triton kerenl 接收的是指向张量 首元素的指针（pointer） 以及描述张量在各个维度上如何步进的 stride 信息，这些 stride 信息使我们能够正确地在内存中沿着指定维度移动

我们可以利用这些 stride 来加载与当前 tile 对应的 x x x 的子张量，具体来说，Triton 使用 program ID 来划分工作负载：例如，第 i i i 个程序实例负责处理 x x x 中第 i i i 个 tile 的行。在这个简单实例中，Triton 与 PyTorch 前向计算的主要区别在于 Triton 需要显式地进行 指针运算 并显式地执行 内存加载（load）和存储（store）

为了简化这些繁琐的指针操作，我们将使用 Triton 提供的 block pointer 抽象 ，即 t1.make_block_ptr，当然，这也意味着在正式计算之前，我们需要进行一些额外的设置来构造这些 block pointer

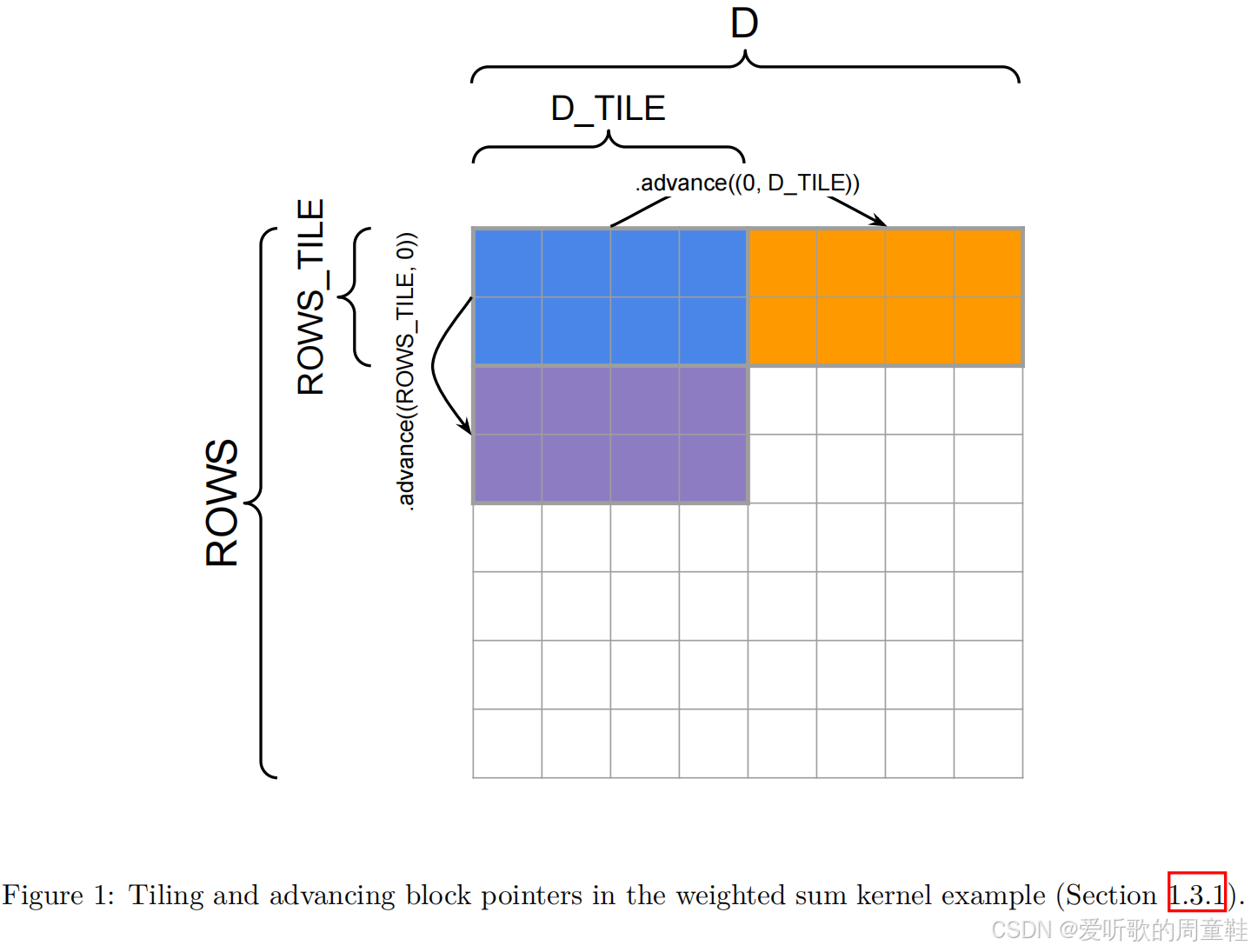
关于 tile 划分方式以及 block pointer 如何在内存中推进可以参考 Figure 1，基于上述说明，加权求和函数在 Triton 中的实现代码如下：

import triton
import triton.language as tl

@triton.jit
def weighted_sum_fwd(
    x_ptr, weight_ptr,    # Input pointers
    output_ptr,           # Output pointer
    x_stride_row, x_stride_dim,   # Strides tell us how to move one element in each axis of a tensor
    weight_stride_dim,            # Likely 1
    output_stride_row,             # Likely 1
    ROWS, D,
    ROWS_TILE_SIZE: tl.constexpr, D_TILE_SIZE: tl.constexpr,  # Tile shapes must be known at compile time
):
    # Each instance will compute the weighted sum of a tile of rows of x.
    # tl.program_id() gives us a way to check which thread block we're running in.
    row_tile_idx = tl.program_id(0)

    # Block pointers give us a way to select from an ND region of memory
    # and move our selection around.
    # The block pointer must know:
    # - The pointer to the first element of the tensor
    # - The overall shape of the tensor to handle out-of-bounds access
    # - The strides of each dimension to use the memory layout properly
    # - The ND coordinates of the starting block, i.e., "offsets"
    # - The block shape to load/store at a time
    # - The order of the dimensions in memory from major to minor
    #   axes = np.argsort(strides) for optimizations, especially useful on H100

    x_block_ptr = tl.make_block_ptr(
        x_ptr,
        shape=(ROWS, D,),
        strides=(x_stride_row, x_stride_dim),
        offsets=(row_tile_idx * ROWS_TILE_SIZE, 0),
        block_shape=(ROWS_TILE_SIZE, D_TILE_SIZE),
        order=(1, 0),
    )

    weight_block_ptr = tl.make_block_ptr(
        weight_ptr,
        shape=(D,),
        strides=(weight_stride_dim,),
        offsets=(0,),
        block_shape=(D_TILE_SIZE,),
        order=(0,),
    )

    output_block_ptr = tl.make_block_ptr(
        output_ptr,
        shape=(ROWS,),
        strides=(output_stride_row,),
        offsets=(row_tile_idx * ROWS_TILE_SIZE,),
        block_shape=(ROWS_TILE_SIZE,),
        order=(0,),
    )

    # Initialize a buffer to write to
    output = tl.zeros((ROWS_TILE_SIZE,), dtype=tl.float32)

    for i in range(tl.cdiv(D, D_TILE_SIZE)):
        # Load the current block pointer
        # Since ROWS_TILE_SIZE might not divide ROWS, and D_TILE_SIZE might not divide D,
        # we need boundary checks for both dimensions.
        row = tl.load(x_block_ptr, boundary_check=(0, 1), padding_option="zero")   # (ROWS_TILE_SIZE, D_TILE_SIZE)
        weight = tl.load(weight_block_ptr, boundary_check=(0,), padding_option="zero")  # (D_TILE_SIZE,)

        # Compute the weighted sum of the row.
        output += tl.sum(row * weight[None, :], axis=1)

        # Move the pointers to the next tile.
        # These are (rows, columns) coordinate deltas.
        x_block_ptr = x_block_ptr.advance((0, D_TILE_SIZE))        # Move by D_TILE_SIZE in the last dimension
        weight_block_ptr = weight_block_ptr.advance((D_TILE_SIZE,))  # Move by D_TILE_SIZE

    # Write output to the output block pointer (a single scalar per row).
    # Since ROWS_TILE_SIZE might not divide ROWS, we need boundary checks.
    tl.store(output_block_ptr, output, boundary_check=(0,))

现在，我们将把这个 Triton kernel 封装进一个 PyTorch 的 Autograd 函数 中，使其能够与 PyTorch 正常协同工作，也就是说：以 Tensor 作为输入、输出一个 Tensor，并且在反向传播阶段能够与 autograd 引擎一起工作

class WeightedSumFunc(torch.autograd.Function):
    @staticmethod
    def forward(ctx, x, weight):
        # Cache x and weight to be used in the backward pass, when we
        # only receive the gradient wrt. the output tensor, and
        # need to compute the gradients wrt. x and weight.
        D, output_dims = x.shape[-1], x.shape[:-1]

        # Reshape input tensor to 2D
        input_shape = x.shape
        x = rearrange(x, "... d -> (...) d")

        ctx.save_for_backward(x, weight)

        assert len(weight.shape) == 1 and weight.shape[0] == D, "Dimension mismatch"
        assert x.is_cuda and weight.is_cuda, "Expected CUDA tensors"
        assert x.is_contiguous(), "Our pointer arithmetic will assume contiguous x"

        ctx.D_TILE_SIZE = triton.next_power_of_2(D) // 16  # Roughly 16 loops through the embedding dimension
        ctx.ROWS_TILE_SIZE = 16  # Each thread processes 16 batch elements at a time
        ctx.input_shape = input_shape

        # Need to initialize empty result tensor. Note that these elements are not necessarily 0!
        y = torch.empty(output_dims, device=x.device)

        # Launch our kernel with n instances in our 1D grid.
        n_rows = y.numel()
        weighted_sum_fwd[(cdiv(n_rows, ctx.ROWS_TILE_SIZE),)](
            x, weight,
            y,
            x.stride(0), x.stride(1),
            weight.stride(0),
            y.stride(0),
            ROWS=n_rows, D=D,
            ROWS_TILE_SIZE=ctx.ROWS_TILE_SIZE, D_TILE_SIZE=ctx.D_TILE_SIZE,
        )

        return y.view(input_shape[:-1])

请注意，当我们以 weighted_sum_fwd[(cdim(n_rows, ctx.ROWS_TILE_SIZE),)](...) 的形式调用 Triton kernel 时，实际上是通过传入 (cdiv(n_rows, ctx.ROWS_TILE_SIZE),) 这个元组，定义了一个所谓的 launch grid（线程块网格） ，在 kernel 内部，我们可以通过 t1.program_id(0) 来获取当前线程块在这个 grid 中的索引，从而确定当前线程块负责处理哪一段数据

Backward pass

由于我们正在定义 自己的自定义 kernel ，因此也需要 自己实现反向传播函数

在前向传播中，我们给定了层的输入，并计算得到了对应的输出，而在反向传播阶段，需要回忆的是：我们会得到目标函数关于该层输出的梯度 ，并需要进一步计算 关于每个输入的梯度 。在我们的例子中，该操作的输入包括一个矩阵 x ∈ R n × h x\in R^{n\times h} x∈Rn×h 以及一个权重向量 w ∈ R h w \in \mathrm{R}^h w∈Rh

为了简化表述，我们将该操作记为 f ( x , w ) f(x,w) f(x,w)，其输出位于 R n \mathrm{R}^n Rn 中，假设我们已经得到了 ∇ f ( x , w ) L \nabla_{f(x,w)} \mathcal{L} ∇f(x,w)L 即损失函数 L \mathcal{L} L 关于该层输出的梯度，那么就可以使用 多元链式法则 ，推导出关于输入 x x x 和权重 w w w 的梯度表达式

对输入矩阵 x x x 的梯度为：

( ∇ x L ) i j = ∑ k = 1 n ∂ f ( x , w ) k ∂ x i j ( ∇ f ( x , w ) L ) k = w j ⋅ ( ∇ f ( x , w ) L ) i (2) (\nabla_x \mathcal{L}){ij} = \sum{k=1}^{n} \frac{\partial f(x,w)k}{\partial x{ij}} (\nabla_{f(x,w)} \mathcal{L})k = w_j \cdot (\nabla{f(x,w)} \mathcal{L})_i \tag{2} (∇xL)ij=k=1∑n∂xij∂f(x,w)k(∇f(x,w)L)k=wj⋅(∇f(x,w)L)i(2)

对权重向量 w w w 的梯度为：

( ∇ w L ) j = ∑ i = 1 n ∂ f ( x , w ) i ∂ w j ( ∇ f ( x , w ) L ) i = ∑ i = 1 n x i j ⋅ ( ∇ f ( x , w ) L ) i (3) (\nabla_w \mathcal{L})j = \sum{i=1}^{n} \frac{\partial f(x,w)i}{\partial w_j} (\nabla{f(x,w)} \mathcal{L})i = \sum{i=1}^{n} x_{ij} \cdot (\nabla_{f(x,w)} \mathcal{L})_i \tag{3} (∇wL)j=i=1∑n∂wj∂f(x,w)i(∇f(x,w)L)i=i=1∑nxij⋅(∇f(x,w)L)i(3)

上述结果给出了一个 非常直接的反向传播计算公式 ，对于 x x x 的梯度，我们根据公式 (2)，只需将权重向量 w w w 与输出梯度 ∇ f ( x , w ) L \nabla_{f(x,w)} \mathcal{L} ∇f(x,w)L 进行 外积（outer product） 即可，对于 w w w 的梯度（即 ∇ w L \nabla_{w} \mathcal{L} ∇wL），我们需要将输入梯度与对应的输出行进行逐元素相乘并累加

我们的反向传播 kernel 将从 定义所有必要的 block pointer 开始，随后计算 ∇ x L \nabla_{x} \mathcal{L} ∇xL：

@triton.jit
def weighted_sum_backward(
    x_ptr, weight_ptr,                 # Input
    grad_output_ptr,                   # Grad input
    grad_x_ptr, partial_grad_weight_ptr,  # Grad outputs
    stride_xr, stride_xd,
    stride_wd,
    stride_gr,
    stride_gxr, stride_gxd,
    stride_gwb, stride_gwd,
    NUM_ROWS, D,
    ROWS_TILE_SIZE: tl.constexpr, D_TILE_SIZE: tl.constexpr,
):
    row_tile_idx = tl.program_id(0)
    n_row_tiles = tl.num_programs(0)

    # Inputs
    grad_output_block_ptr = tl.make_block_ptr(
        grad_output_ptr,
        shape=(NUM_ROWS,),
        strides=(stride_gr,),
        offsets=(row_tile_idx * ROWS_TILE_SIZE,),
        block_shape=(ROWS_TILE_SIZE,),
        order=(0,),
    )

    x_block_ptr = tl.make_block_ptr(
        x_ptr,
        shape=(NUM_ROWS, D),
        strides=(stride_xr, stride_xd),
        offsets=(row_tile_idx * ROWS_TILE_SIZE, 0),
        block_shape=(ROWS_TILE_SIZE, D_TILE_SIZE),
        order=(1, 0),
    )

    weight_block_ptr = tl.make_block_ptr(
        weight_ptr,
        shape=(D,),
        strides=(stride_wd,),
        offsets=(0,),
        block_shape=(D_TILE_SIZE,),
        order=(0,),
    )

    grad_x_block_ptr = tl.make_block_ptr(
        grad_x_ptr,
        shape=(NUM_ROWS, D),
        strides=(stride_gxr, stride_gxd),
        offsets=(row_tile_idx * ROWS_TILE_SIZE, 0),
        block_shape=(ROWS_TILE_SIZE, D_TILE_SIZE),
        order=(1, 0),
    )

    partial_grad_weight_block_ptr = tl.make_block_ptr(
        partial_grad_weight_ptr,
        shape=(n_row_tiles, D),
        strides=(stride_gwb, stride_gwd),
        offsets=(row_tile_idx, 0),
        block_shape=(1, D_TILE_SIZE),
        order=(1, 0),
    )

    for i in range(tl.cdiv(D, D_TILE_SIZE)):
        grad_output = tl.load(
            grad_output_block_ptr,
            boundary_check=(0,),
            padding_option="zero",
        )  # (ROWS_TILE_SIZE,)

        # Outer product for grad_x
        weight = tl.load(
            weight_block_ptr,
            boundary_check=(0,),
            padding_option="zero",
        )  # (D_TILE_SIZE,)
        grad_x_row = grad_output[:, None] * weight[None, :]
        tl.store(
            grad_x_block_ptr,
            grad_x_row,
            boundary_check=(0, 1),
        )

        # Reduce as many rows as possible for the grad_weight result
        row = tl.load(
            x_block_ptr,
            boundary_check=(0, 1),
            padding_option="zero",
        )  # (ROWS_TILE_SIZE, D_TILE_SIZE)
        grad_weight_row = tl.sum(
            row * grad_output[:, None],
            axis=0,
            keep_dims=True,
        )
        tl.store(
            partial_grad_weight_block_ptr,
            grad_weight_row,
            boundary_check=(1,),
        )

        # Move the pointers to the next tile along D
        x_block_ptr = x_block_ptr.advance((0, D_TILE_SIZE))
        weight_block_ptr = weight_block_ptr.advance((D_TILE_SIZE,))
        partial_grad_weight_block_ptr = partial_grad_weight_block_ptr.advance((0, D_TILE_SIZE))
        grad_x_block_ptr = grad_x_block_ptr.advance((0, D_TILE_SIZE))

计算 ∇ x \nabla_x ∇x 的梯度是比较简单的，我们只需将结果写入输出张量中对应的 tile 即可，然而，计算 ∇ w \nabla_w ∇w 则要复杂一些，每个 kernel 实例只负责处理 x x x 的一个行 tile，但现在我们需要对 所有行 进行累加

我们并不会在 backward kerenl 内部直接完成这一全局求和，而是假设 partial_grad_weight_ptr 保存的是一个形状为 n_row_tiles × H \times H ×H 的矩阵，其中第一维只在单个行 tile 内完成了归约，也就是说，我们先在 当前行 tile 内进行归约，然后将结果写入该张量

在 kernel 外部，我们再使用 torch.sum 对所有行 tile 的结果进行汇总（当然，如果愿意的话，我们也完全可以为这一步单独再写一个 kernel），从而得到最终的 ∇ w \nabla_w ∇w，这样一来，autograd.Function 中的最后一部分实现就相对简单了

class WeightedSumFunc(torch.autograd.Function):
    @staticmethod
    def forward(ctx, x, weight):
        # ... (defined earlier)

    @staticmethod
    def backward(ctx, grad_out):
        x, weight = ctx.saved_tensors
        ROWS_TILE_SIZE, D_TILE_SIZE = ctx.ROWS_TILE_SIZE, ctx.D_TILE_SIZE  # These don't have to be the same
        n_rows, D = x.shape

        # Our strategy is for each thread block to first write to a partial buffer,
        # then we reduce over this buffer to get the final gradient.
        partial_grad_weight = torch.empty((cdiv(n_rows, ROWS_TILE_SIZE), D), device=x.device, dtype=x.dtype)
        grad_x = torch.empty_like(x)

        weighted_sum_backward[(cdiv(n_rows, ROWS_TILE_SIZE),)](
            x, weight,
            grad_out,
            grad_x, partial_grad_weight,
            x.stride(0), x.stride(1),
            weight.stride(0),
            grad_out.stride(0),
            grad_x.stride(0), grad_x.stride(1),
            partial_grad_weight.stride(0), partial_grad_weight.stride(1),
            NUM_ROWS=n_rows, D=D,
            ROWS_TILE_SIZE=ROWS_TILE_SIZE, D_TILE_SIZE=D_TILE_SIZE,
        )

        grad_weight = partial_grad_weight.sum(axis=0)
        return grad_x, grad_weight

最后，我们就可以得到一个函数，它的行为方式与 torch.nn.functional 中实现的函数非常相似：

f_weightedsum = WeightedSumFunc.apply

现在，对两个 PyTorch 张量 x x x 和 w w w 调用 f_weightedsum，将会得到如下形式的输出张量：

tensor([ 90.8563, -93.6815, -80.8884, ..., 103.4840, -21.4634, -24.0192],
       device='cuda:0', grad_fn=<WeightedSumFuncBackward>)

请注意张量上附带的 grad_fn，这表明当该张量出现在计算图中时，PyTorch 知道在反向传播阶段应该调用哪个函数，这也标注着我们已经完成了 weighted sum 运算的 Triton 实现

2.2 FlashAttention-2 Forward Pass

你将使用一个显著改进的 Triton 实现 来替换原来的 PyTorch 注意力实现，将实现遵循 FlashAttention-2 方法 [Dao 2023]，FlashAttention-2 采用了一些关键技巧，将前向传播过程按 tile（分块） 方式进行计算，从而实现高效的内存访问模式，并避免在全局内存中显式构造完整的注意力矩阵

在深入本节之前，我们 强烈建议 至少先阅读原始的 FlashAttention 论文 [Dao+ 2022]，该论文能够帮助你理解 FlashAttention 背后的核心思想：在跨 tile 的过程中以在线（online）的方式计算 softmax ，这一技术最早由 [Milakov and Gimelshein, 2018] 提出，是 FlashAttention 能够高效扩展到长序列的关键。此外，我们也推荐阅读 [He 2022] 的相关资料，以获得更多关于 GPU 实际如何执行 PyTorch 代码的直觉理解

Understanding inefficiencies in vanilla attention.

回顾一下注意力机制在 前向传播 中的计算形式（暂时忽略 mask），可以写为：

S = Q K ⊤ / d P i j = softmax j ( S ) i j O = P V \begin{align} \mathbf{S} &= \mathbf{QK}^{\top}/\sqrt{d} \tag{4} \\ \mathbf{P}_{ij} &= \text{softmax}j(\mathbf{S}){ij} \tag{5} \\ \mathbf{O} &= \mathbf{PV} \tag{6} \end{align} SPijO=QK⊤/d =softmaxj(S)ij=PV(4)(5)(6)

对应的 标准反向传播 过程为：

d V = P ⊤ d O d P = d O V ⊤ d S i = d s o f t m a x ( d P i ) = ( d i a g ( P i ) − P i P i ⊤ ) d P i d Q = d S K / d d K = d S ⊤ Q / d \begin{align*} \mathbf{dV} &= \mathbf{P}^{\top} \mathbf{dO} \tag{7} \\ \mathbf{dP} &= \mathbf{dO} \mathbf{V}^{\top} \tag{8} \\ \mathbf{dS}_i &= \mathrm{dsoftmax}(\mathbf{dP}_i) = \left(\mathrm{diag}(\mathbf{P}_i)-\mathbf{P}_i\mathbf{P}_i^{\top}\right)\mathbf{dP}_i \tag{9} \\ \mathbf{dQ} &= \mathbf{dSK} / \sqrt{d} \tag{10} \\ \mathbf{dK} &= \mathbf{dS}^{\top}\mathbf{Q} / \sqrt{d} \tag{11} \end{align*} dVdPdSidQdK=P⊤dO=dOV⊤=dsoftmax(dPi)=(diag(Pi)−PiPi⊤)dPi=dSK/d =dS⊤Q/d (7)(8)(9)(10)(11)

从上述公式可以看出，反向传播过程依赖于前向传播中产生的一些非常大的激活张量 ，例如，在公式 (7) 中计算 d V \mathbf{dV} dV 时，需要用到注意力权重矩阵 P \mathbf{P} P，该矩阵的形状为 (batch_size, n_heads, seq_len, seq_len) ，其大小会随着序列长度 以平方级别增长，这正是我们在对长序列注意力进行基准测试时遇到严重内存问题的根本原因

在原始注意力的前向和反向传播中，为了在 片上 SRAM 与 GPU HBM 之间传输 P \mathbf{P} P 以及其他大型激活张量，会付出非常显著的内存 I/O 成本。在标准实现中，这类数据传输会发生多次：例如，一个典型的反向传播实现会在计算公式 (7) 和 (9) 时，从 HBM 中反复读取 P \mathbf{P} P

FlashAttention 的核心目标 ，正是避免将完整注意力矩阵 P \mathbf{P} P 写入和读取 HBM，从而降低内存 I/O 成本和峰值显存占用。为此，FlashAttention 采用了三项关键技术：分块（tiling）、重计算（recomputation）以及算子融合（operator fusion）

Tiling.

为了避免在 HBM（高带宽显存）中反复读写完整的注意力矩阵，我们在不访问完整输入的情况下完成 softmax 的归约计算。具体来说，我们重新组织注意力计算流程，将输入划分为若干 tile（分块），并对这些输入块进行多次遍历，从而逐步、增量地完成 softmax 归约操作

Recomputation.

我们避免将形状为 (batch_size, n_heads, seq_len, seq_len) 的巨大中间注意力矩阵存储在 HBM 中，取而代之的是，只在 HBM 中保存部分 激活检查点（activation checkpoints），并在反向传播阶段重新计算前向传播中的部分结果，以获取计算梯度所需的其他激活值

FlashAttention-2 还会额外存储注意力分数的 log-sum-exp 值 L L L，用于简化反向传播的计算，其表达式为：

L i = log ⁡ ( ∑ j exp ⁡ ( S i j ) ) (12) L_i = \log \left( \sum_j \exp(\mathbf{S}_{ij}) \right) \tag{12} Li=log(j∑exp(Sij))(12)

在最终的 kernel 中，我们将以 在线（online） 的方式计算该值，但最终结果应当与完整计算得到的结果一致

通过 分块（tiling）与重计算（recomputation） 的结合，我们的内存 I/O 开销和峰值显存使用将不再依赖于序列长度的平方，因此可以支持更长的序列长度

Operator fusion.

最后，我们通过在 单个 kernel 中完成所有操作，避免了对注意力矩阵以及其他中间激活结果的重复内存 I/O，这种方式被称为 算子融合（operator fusion） 或 kernel 融合。我们将为前向传播编写一个单一的 Triton kernel，在其中完成注意力计算所涉及的全部操作，从而将 HBM 与 SRAM 之间的数据传输降到最低

算子融合在一定程度上得益于 重计算（recomputation） ：因为我们可以避免将每一个中间激活都存储到 HBM 中，从而避免了常规实现中大量的内存读写开销，如果你希望对这些技术有更深入的理解，可以参考 FlashAttention 相关论文 [Dao+ 2022] [Dao 2023]

Backward pass with recomputation.

借助前向传播中保存的 L L L，我们可以进行必要的重计算，并高效地完成反向传播。在开始反向传播之前，我们会先在全局内存中预计算 D = r o w s u m ( O ∘ d O ) D = \mathrm{rowsum} \left( \mathbf{O} \circ \mathbf{dO}\right) D=rowsum(O∘dO)，其中 ∘ \circ ∘ 表示逐元素乘法。注意该表达式等价于 r o w s u m ( P ∘ d P ) \mathrm{rowsum} \left( \mathbf{P} \circ \mathbf{dP}\right) rowsum(P∘dP)，因为 P d P ⊤ = P ( d O V ⊤ ) ⊤ = ( P V ) d O ⊤ = O d O ⊤ \mathbf{PdP}^{\top} = \mathbf{P}\left(\mathbf{dOV}^{\top}\right)^{\top}=(\mathbf{PV})\mathbf{dO}^{\top}=\mathbf{OdO}^{\top} PdP⊤=P(dOV⊤)⊤=(PV)dO⊤=OdO⊤，并且对任意矩阵 A , B \mathbf{A},\mathbf{B} A,B，都有 r o w s u m ( A ∘ B ) = d i a g ( A B ⊤ ) \mathrm{rowsum}(\mathbf{A}\circ\mathbf{B})=\mathrm{diag}(\mathbf{AB}^{\top}) rowsum(A∘B)=diag(AB⊤)

有了向量 L L L 和 D D D 之后，反向传播就可以在 不显式计算 softmax 的情况下完成，完整的反向计算流程如下：

S = Q K ⊤ / d P i j = exp ⁡ ( S i j − L i ) d V = P ⊤ d O d P = d O V ⊤ d S i j = P i j ∘ ( d P i j − D i ) d Q = d S K / d d K = d S ⊤ Q / d \begin{align} \mathbf{S} &= \mathbf{QK}^{\top} / \sqrt{d} \tag{13} \\ \mathbf{P}{ij} &= \exp(\mathbf{S}{ij} - L_i) \tag{14} \\ \mathbf{dV} &= \mathbf{P}^{\top} \mathbf{dO} \tag{15} \\ \mathbf{dP} &= \mathbf{dO} \mathbf{V}^{\top} \tag{16} \\ \mathbf{dS}{ij} &= \mathbf{P}{ij} \circ (\mathbf{dP}_{ij} - D_i) \tag{17} \\ \mathbf{dQ} &= \mathbf{dSK}/ \sqrt{d} \tag{18} \\ \mathbf{dK} &= \mathbf{dS}^{\top} \mathbf{Q} / \sqrt{d} \tag{19} \end{align} SPijdVdPdSijdQdK=QK⊤/d =exp(Sij−Li)=P⊤dO=dOV⊤=Pij∘(dPij−Di)=dSK/d =dS⊤Q/d (13)(14)(15)(16)(17)(18)(19)

可以看到，这一计算流程 不需要在前向传播阶段将注意力概率矩阵 P \mathbf{P} P 存储在 HBM 中 ，在反向传播中，我们只需利用激活值 Q \mathbf{Q} Q、 K \mathbf{K} K 以及 L L L，即可通过公式 (13) 和 (14) 重新计算出 P \mathbf{P} P

Details of the flash attention forward pass.

现在我们已经从整体上理解了 FlashAttention-2 中所使用的关键技术，接下来将深入分析你需要实现的 FA2 前向传播核函数 的具体细节

为了避免在 HBM（高带宽显存） 与计算单元之间频繁地读写完整的注意力矩阵，我们希望采用 分块（tiling） 的方式来计算注意力，也就是说：每个输出块都可以相互独立地计算 。理想情况下，我们希望在查询（query）维度和键（key）维度上同时进行分块，从而逐块地计算注意力矩阵 P \mathbf{P} P

然而，在对注意力分数矩阵 S \mathbf{S} S 应用 softmax 时，我们需要对 整行的 S \mathbf{S} S 进行归一化，以计算 softmax 的分母，这意味我们 无法直接在分块的情况下独立地计算 P \mathbf{P} P，FlashAttention-2 正是通过一种称为 在线 softmax（online softmax） 的技术来解决这一问题

在接下来的描述中，我们使用下标 i i i 表示当前正在处理的 query tile ，使用上标 j j j 表示当前的 key tile ，沿着 query 维度的 tile 大小记为 B q B_q Bq，沿着 key 维度的 tile 大小记为 B k B_k Bk，需要注意的是，我们 不会在隐藏维度 d d d 上进行分块

在计算过程中，我们还会维护两个 按行更新的运行中间量：

• m i ( j ) ∈ R B q m_i^{(j)} \in \mathbb{R}^{B_q} mi(j)∈RBq：表示当前行的 运行最大值（running maximum）
• l i ( j ) ∈ R B q l_i^{(j)} \in \mathbb{R}^{B_q} li(j)∈RBq：表示当前行 softmax 分母的一个 运行代理量

其中， m i ( j ) m_i^{(j)} mi(j) 用于保证 softmax 的数值稳定性，这一点你在 Assignment 1 的 softmax 实现中已经见过

当我们依次处理每一个 key tile（即 j j j 递增）时，会不断更新 m i ( j ) m_i^{(j)} mi(j)，借助这个运行最大值，我们可以计算 未归一化的 softmax 分子：

P ~ i ( j ) = exp ⁡ ( S i j − m i ( j ) ) \tilde{\mathbf{P}}{i}^{(j)} = \exp(\mathbf{S}{ij} - m_i^{(j)}) P~i(j)=exp(Sij−mi(j))

而 l i ( j ) l_i^{(j)} li(j) 则作为 softmax 分母的运行累积量，通过未归一化的 softmax 值进行更新，其更新方式为：

l i ( j ) = exp ⁡ ( m i ( j − 1 ) − m i ( j ) ) l i ( j − 1 ) + r o w s u m ( P ~ i ( j ) ) l_i^{(j)} = \exp(m_i^{(j-1)} - m_i^{(j)}) l_i^{(j-1)} + \mathrm{rowsum} \left( \tilde{\mathbf{P}}_{i}^{(j)}\right) li(j)=exp(mi(j−1)−mi(j))li(j−1)+rowsum(P~i(j))

当所有 key tiles 都处理完成后，我们会得到最终的 l i ( T k ) l_i^{(T_k)} li(Tk)，其中 T k T_k Tk 表示 key tile 的总数量，此时，在将最终输出写回之前，需要使用该值对结果进行一次最终归一化

Algorithm 1 给出了该前向传播过程在 GPU 上应如何实现的完整示意：

在开始用 Triton 实现前向传播之前，我们先汇总一些编写 Triton kernel 时的通用技巧和经验

---

Triton Tips and Tricks

• 你可以在 Triton 中使用 tl.device_print 来进行调试输出，相关文档见：https://triton-lang.org/main/python-api/generated/triton.language.device_print.html，另外，还有一个环境变量 TRITON_INTERPRET=1 可以让 Triton kernel 在 CPU 上以解释模式运行，尽管该模型目前存在一些已知问题，但在调试时仍然可能有帮助

• 在定义 block pointer（块指针）时，一定要确保它们的 offset 设置正确，并且 block 的偏移量已经乘以对应的 tile 尺寸，否则很容易出现越界或访问错误的问题

• 线程块（block）的 launch grid 通过如下方式设置：

  kernel_fn[(launch_grid_d1, launch_grid_d2, ...)](...arguments...)

  这种调用方式通常出现在 torch.autograd.Function 的子类方法中，正如我们在前面的 weighted sum 示例中看到的那样

• 在 Triton 中执行矩阵乘法时，应使用 t1.dot

• 如果需要推进一个 block pointer 到下一个 tile，可以使用：

  *_block_ptr = *_block_ptr.advance(...)

  来完成指针的前移操作

---

Problem (flash_forward): 15 points

(a) 编写一个 纯 PyTorch（不使用 Triton） 的 autograd.Function，用于实现 FlashAttention-2 的前向传播，该实现会比常规的 PyTorch 注意力实现慢得多，但它将有助于你调试后续的 Triton kernel

你的实现应当接收输入 Q , K , V \mathbf{Q},\mathbf{K},\mathbf{V} Q,K,V 以及一个标志位 is_causal，并输出结果 O \mathbf{O} O 以及 logsumexp 值 L L L，在本题中，你可以忽略 is_causal 标志。autograd.Function 的 forward 方法随后应当通过 save_for_backward 保存 L , Q , K , V , O L,\mathbf{Q},\mathbf{K},\mathbf{V},\mathbf{O} L,Q,K,V,O，以供反向传播阶段使用

请注意，autograd.Function 的 forward 方法始终将 context（ctx） 作为第一个参数，任何 autograd.Function 类都需要实现一个 backward 方法，不过在当前阶段你可以让它直接抛出 NotImplementedError。如果你需要一个对照实现，可以在 PyTorch 中实现公式 (4) 到 (6) 以及 (12)，并将其输出与你的实现进行比较

该接口定义为：

def forward(ctx, Q, K, V, is_causal=False)

tile 的尺寸可以由你自行决定，但请确保 至少为 16x16 ，我们在测试中始终使用 维度为 2 的整数次幂且不小于 16 的输入，因此你无需担心越界访问的问题

Deliverable ：一个 torch.autograd.Function 的子类，实现 FlashAttention-2 的前向传播 ，为了测试你的代码，请实现 [adapters.get_flashattention_autograd_function_pytorch]，然后运行：

uv run pytest -k test_flash_forward_pass_pytorch

并确保你的实现能够通过测试。

(b) 接下来，请按照 Algorithm 1 编写一个 Triton kernel ，用于实现 FlashAttention-2 的前向传播 。随后，请再编写一个继承自 torch.autograd.Function 的子类，在其 forward 方法中调用你刚刚实现的 融合（fused）Triton kernel，而不是再用 PyTorch 逐步计算结果

下面是一些针对该问题的调试与实现建议：

• 为了便于调试，我们建议将你在 Triton 中执行的每一步操作结果，与 (a) 部分中你实现的 tiled Pytorch 版本 逐一进行对比

• kernel 的 launch grid 应设置为 ( T q , b a t c h _ s i z e ) (T_q, \mathrm{batch\_size}) (Tq,batch_size)，这意味着每一个 Triton program instance 只会处理 一个 batch 索引 ，并且只会读取和写入 一个 query tile 中对应的 Q , O \mathbf{Q},\mathbf{O} Q,O 和 L L L

• kernel 内部应当 只包含一个循环 ，该循环沿着 key 维度遍历所有 key tiles，即 1 ≤ j ≤ T k 1 \le j \le T_k 1≤j≤Tk

• 在循环结束时，记得 推进（advance）所有 block pointer，以指向下一个 tile

• 请使用下面给出的 函数声明模板（我们已经为你提供了部分 block pointer 的定义，其余指针的设置方式应当可以自行推导出来）：

  @triton.jit
  def flash_fwd_kernel(
      Q_ptr, K_ptr, V_ptr,
      O_ptr, L_ptr,
      stride_qb, stride_qq, stride_qd,
      stride_kb, stride_kk, stride_kd,
      stride_vb, stride_vk, stride_vd,
      stride_ob, stride_oq, stride_od,
      stride_lb, stride_lq,
      N_QUERIES, N_KEYS,
      scale,
      D: tl.constexpr,
      Q_TILE_SIZE: tl.constexpr,
      K_TILE_SIZE: tl.constexpr,
  ):

  其中， s c a l e = 1 d \mathrm{scale}=\frac{1}{\sqrt{d}} scale=d 1，而 Q_TILE_SIZE 和 K_TILE_SIZE 分别对应 B q B_q Bq 和 B k B_k Bk，这些参数后续都可以根据性能需要进行调优

下面是一些额外的实现建议，可以帮助你避免数值精度方面的问题：

• 位于片上（on-chip）的缓冲区 ( O , l , m ) (\mathbf{O},l,m) (O,l,m) 应当使用 tl.float32 作为数据类型，如果你在向输出缓冲区中进行累加，请使用 acc 参数，例如 acc = tl.dot(..., acc=acc)
• 在将 P ~ i ( j ) \tilde{\mathrm{P}}_i^{(j)} P~i(j) 与 V ( j ) \mathbf{V}^{(j)} V(j) 相乘之前，应当先将 P ~ i ( j ) \tilde{\mathrm{P}}_i^{(j)} P~i(j) 转换为与 V ( j ) \mathbf{V}^{(j)} V(j) 相同的数据类型；在将 O \mathbf{O} O 写回全局内存之前，也应将其转换为合适的数据类型。类型转换可以通过 tensor.to 来完成，你可以通过 tensor.dtype 获取一个 tensor 的数据类型，而 block pointer 或普通指针的数据类型可以通过 *_block_ptr.type.element_ty 获取

Deliverable ：实现一个继承自 torch.autograd.Function 的子类，在其 forward 中调用你编写的 Triton kernel ，从而实现 FlashAttention-2 的前向传播 ，实现 [adapters.get_flash_autograd_function_triton] 后，请运行以下测试命令以验证正确性：

uv run pytest -k test_flash_forward_pass_triton

(c) 请在你的 autograd.Function 实现中，将 因果掩码（causal masking）作为最后一个参数 加入，该参数应为一个布尔类型标志，当其设置为 True 时，启用用于因果掩码的索引比较逻辑。你的 Triton kernel 需要有一个与之对应的额外参数 is_causal: tl.constexpr（这是类型注解所必需的）

在 Triton 中需要为 queries 和 keys 构造合适的索引向量，将它们与一个大小为 B q × B k B_q \times B_k Bq×Bk 的方形掩码进行比较，对于被掩码的位置，在注意力得分矩阵 S i ( j ) \mathbf{S}_i^{(j)} Si(j) 的对应元素上 加上常数值 -1e6 。请务必在 forward 中保存该掩码标志，以便在反向传播阶段使用 ctx.is_causal = is_causal

Deliverable ：为你的 torch.autograd.Function 子类增加一个可选的因果掩码标志，使其能够通过你实现的 Triton kernel 执行带因果掩码的 FlashAttention-2 前向传播。请确保该标志是可选参数，默认值为 False，以保证之前的所有测试仍然可以通过。

Problem (flash_backward): 5 points

Implementing the backward pass with recomputation

注意，与公式 (7)-(11) 中给出的标准反向传播不同，我们可以通过 重计算（recomputation）来避免在反向传播阶段执行 softmax 运算 （如公式 (13)-(19) 所示），这意味着反向传播可以通过一个相对简单的 kernel 来完成，不需要任何在线 softmax 技巧。因此，在这一部分，你可以直接通过在一个普通的 PyTorch 函数（而不是 Triton kernel）上调用 torch.compile 来实现反向传播

请使用 PyTorch（而非 Triton） 和 torch.compile 为你的 FlashAttention-2 autograd.Function 实现反向传播。你的实现应当接收张量 Q , K , V , O , d O \mathbf{Q},\mathbf{K},\mathbf{V},\mathbf{O},\mathbf{dO} Q,K,V,O,dO 和 L L L 作为输入，并返回 d Q , d K \mathbf{dQ},\mathbf{dK} dQ,dK 和 d V \mathbf{dV} dV。请注意在计算过程中需要显式地计算并使用向量 D D D，你可以按照公式 (13)-(19) 中给出的计算流程来实现反向传播

Deliverable：为了测试你的实现，请运行以下命令：

uv run pytest -k test_flash_backward

并确保你的实现能够顺利通过测试。

Problem (flash_benchmarking): 5 points

接下来，我们来比较你 基于 Triton 的 FlashAttention-2 实现与使用 PyTorch 实现的标准 Attention 在性能上的差异

(a) 使用 triton.testing.do_bench 编写一个 性能基准测试脚本，比较以下两种实现的性能：

• 你实现的 Triton 版 FlashAttention-2 的前向和反向传播
• 普通的 PyTorch Attention 实现（即不使用 FlashAttention）

具体要求如下：

• 你需要给出一张结果表，包含 前向传播（forward）、反向传播（backward）以及端到端前向 + 反向传播（end-to-end forward-backward） 的延迟；
• 对 Triton 实现 和 PyTorch 实现 都需要分别测量上述三类延迟
• 在开始基准测试之前，需随机生成所有必要的输入；
• 基准测试需在 单张 H100 GPU 上运行；
• 始终使用 batch size = 1 ，并启用 因果掩码（causal masking）
• 在测试中遍历如下组合（笛卡儿积）：
  • 序列长度：从 128 到 65536，取 2 的幂
  • 嵌入维度：从 16 到 128，取 2 的幂
  • 数据精度 ：torch.bfloat16 和 torch.float32
• 你可能需要根据输入规模调整 tile size

Deliverable：提交一张结果表，对比你实现的 FlashAttention-2 与 PyTorch Attention 在上述设置下的性能，并分别报告前向延迟、反向延迟、端到端前向+反向延迟。

2.3 FlashAttention-2 Leaderboard

Assignment 2 的排行榜将测试你所实现的 FlashAttention-2 的速度表现（包括前向和反向传播），我们鼓励你尽可能使用各种技巧来进一步提升实现的性能

需要注意的限制条件如下：

• 不允许改变函数的输入/输出接口
• 必须使用 Triton（而非）CUDA 实现
• 输入将在 BF16 精度 + causal masking 条件下进行测试
• 你的实现必须通过与普通实现完全一致的正确性测试
• 实现必须是你 原创的，不能使用已有的第三方实现

性能测试将在一块 H100 GPU 上进行，测试配置如下：

• batch size = 1
• 查询、键和值（Q/K/V）的序列长度均为 16,384
• d model = 1024 d_{\text{model}}=1024 dmodel=1024
• head 数为 16

我们将验证前 5 名提交的正确性和性能，测试代码形式如下：

def test_timing_flash_forward_backward():
    n_heads = 16
    d_head = 64
    sequence_length = 16384
    q, k, v = torch.randn(
        3, n_heads, sequence_length, d_head,
        device='cuda', dtype=torch.bfloat16, requires_grad=True
    )

    flash = torch.compile(FlashAttention2.apply)

    def flash_forward_backward():
        o = flash(q, k, v, True)
        loss = o.sum()
        loss.backward()

    results = triton.testing.do_bench(
        flash_forward_backward,
        rep=10000,
        warmup=1000
    )
    print(results)

在你本地测试时，可以适当缩短 repetition 和 warmup 时间（单位为毫秒）

你可以考虑以下方向来进一步提升性能：

• 调整 kernel 的 tile size（推荐使用 Triton autotune）
• 微调更多 Triton kernel 的配置参数
• 使用 Triton 实现反向传播 ，而不仅仅依赖 torch.compile（见下文 2.4 小节）
• 在反向传播中对输入执行 两次遍历 ：一次用于计算 d Q \mathbf{dQ} dQ，另一次用于计算 d K \mathbf{dK} dK 和 d V \mathbf{dV} dV，从而避免 block 之间的原子操作或同步
• 在 casual masking 场景下，提前终止 某些 program instance，跳过那些必然全为零的 tile
• 将 非 mask 的 tile 与对角线 tile 分开处理：前者完全不需要索引比较，后者只需一次比较
• 在 H100 上使用 TMA（Tensor Memory Accelerator） 功能，可参考相关教程 [tutorial] 采用类似模式

2.4 OPTIONAL: Triton backward pass

如果你希望进一步加深对 Triton 的理解，或者想在排行榜中取得更快的成绩，我们在下文中提供了 FlashAttention-2 的 tiled 反向传播实现示例，你可以将其完整地用 Triton 实现。

Algorithm 2 展示了 FlashAttention-2 的反向传播在 Triton 中应当如何实现，一个关键技巧是 对注意力概率矩阵 P \mathbf{P} P 进行两次计算 ：一次用于反向传播中的 d Q \mathbf{dQ} dQ，另一次用于 d K \mathbf{dK} dK 和 d V \mathbf{dV} dV，这样可以避免 thread block 之间的同步，从而显著提升性能

结语

这篇文章我们系统性地梳理了 CS336 Assignment2 中 FlashAttention-2 小节地全部作业要求与设计背景，从标准注意力在长序列场景下面临的显存与内存带宽瓶颈出发，逐步理解了 FlashAttention-2 通过分块（tiling）、在线 softmax、重计算（recomputation）以及算子融合（operator fusion）所构建的整体优化思路。

下篇文章我们就来一起看看 FlashAttention-2 具体该如何实现，敬请期待🤗

参考

• https://github.com/stanford-cs336/assignment2-systems