承接上一篇 CNN 可视化的内容，本节课鲁鹏教授聚焦生成模型核心内容，以无监督学习为基础，从密度估计核心出发，拆解生成模型的分类与典型架构，重点讲解 PixelRNN/CNN 的序列生成逻辑，并深入剖析变分自编码器（VAE）的模型设计、训练原理与应用特点，完整呈现显式密度估计类生成模型的构建思路。
课程链接：
目录
[三、显式可解生成模型：PixelRNN/CNN 的序列生成原理](#三、显式可解生成模型：PixelRNN/CNN 的序列生成原理)
[四、VAE 基础：自编码器的结构与应用局限](#四、VAE 基础：自编码器的结构与应用局限)
[五、VAE 核心设计：从确定编码到概率分布的关键改进](#五、VAE 核心设计：从确定编码到概率分布的关键改进)
[六、VAE 训练：双损失函数与对数似然下界优化](#六、VAE 训练：双损失函数与对数似然下界优化)
[七、VAE 特性：模型优势、局限与应用特点](#七、VAE 特性：模型优势、局限与应用特点)
一、课程基础：无监督学习的核心任务与价值
无监督学习与有监督学习的核心区别在于无标签数据，无需学习 x 到 y 的映射，而是挖掘数据中隐含的模式与结构，是生成模型的学习基础。
其核心典型任务有三类，且各有实际应用价值：
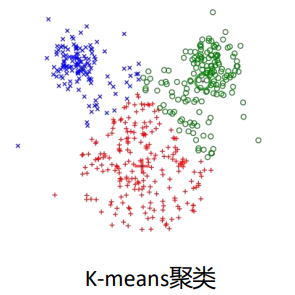
- 聚类：将数据分组，如广告投放中对电视用户聚类，实现同时间段精准投放，提升平台与广告商双方效益；
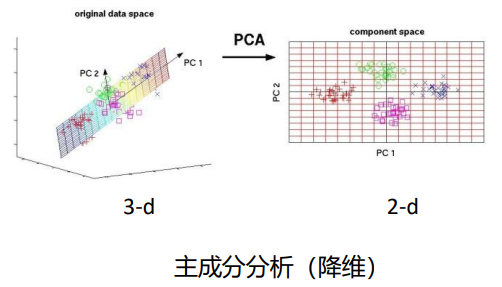
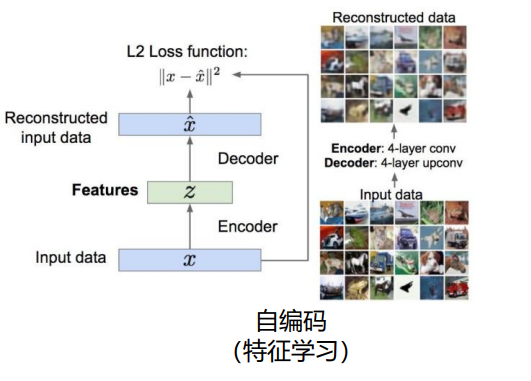
- 降维：将高维数据降至低维并保留核心信息，如 PCA（线性）、自编码器（非线性），解决高维数据噪声多、模型效果差的问题；
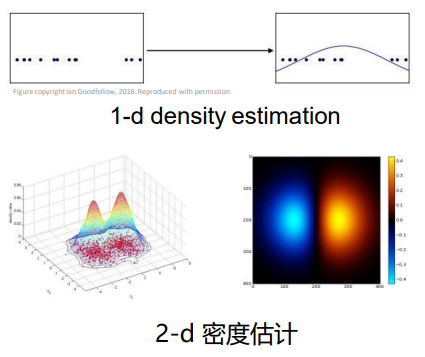
- 密度估计：拟合数据的概率分布，是生成模型的核心基础，为后续贝叶斯决策等任务提供概率密度函数支撑。
二、生成模型定位：以密度估计为核心的样本生成逻辑
生成模型 学习分布并生成同分布样本
生成模型的核心目标是概率密度估计，即学习训练样本的真实分布，进而生成与该分布一致的新样本。
- 密度估计分类：分为显式（可定义分布方程，可计算样本生成概率）和隐式（仅能生成样本，无明确分布方程）两类；
- 生成模型应用：可实现图像合成、图像属性编辑、风格转移等实际场景需求；
- 课程讲解框架：各选取一类典型模型讲解，分别为显式可解的 PixelRNN/CNN、显式需近似求解的 VAE、隐式的 GAN。
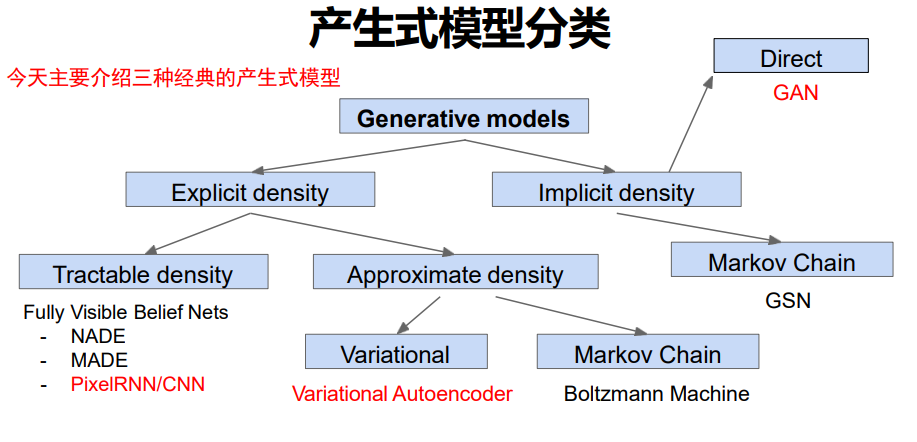生成模型的分类框架
三、显式可解生成模型：PixelRNN/CNN 的序列生成原理
PixelRNN 与 PixelCNN 是显式密度估计中分布方程可解的典型，二者均将图像生成拆解为逐像素的序列生成过程，通过链式准则依次生成像素，且均通过极大似然估计训练，能输出显式的像素生成概率分布。
PixelRNN 与 PixelCNN的核心公式（链式准则）
二者的核心差异与局限性如下：
- PixelRNN ：基于循环神经网络（RNN）处理像素序列，RNN 擅长时序 / 序列任务，但该模型训练和生成速度均较慢；
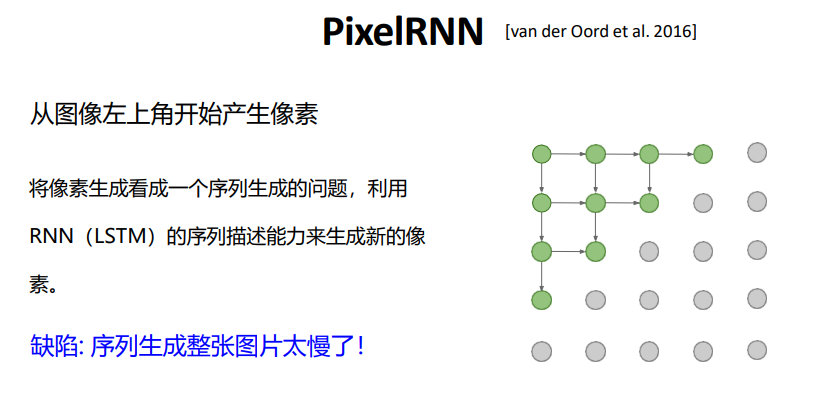PixelRNN - PixelCNN ：基于卷积神经网络（CNN）优化，可批量训练，提升了训练效率，但仍需逐像素生成图像；
PixelCNN - 共同局限：生成速度慢，不适合生成大图，且生成结果可编辑性差，效果远不如主流生成模型。
PixelRNN 与 PixelCNN的优缺点总结
四、VAE 基础：自编码器的结构与应用局限
变分自编码器（Variational Autoencoder，VAE）是融合变分推断与自编码器结构的生成式无监督模型，作为显式密度估计类生成模型的典型，核心用于学习数据概率分布并生成新样本。
VAE（变分自编码器） 基于自编码器改进而来，先掌握自编码器的基础是理解 VAE 的关键，自编码器是实现非线性降维的无监督模型，核心结构与应用存在明显局限：
- 核心结构 ：由编码器和解码器组成，编码器将高维输入映射为低维编码 z，解码器将 z 重构为与输入近似的输出，通过输入与重构的 L2 损失训练；
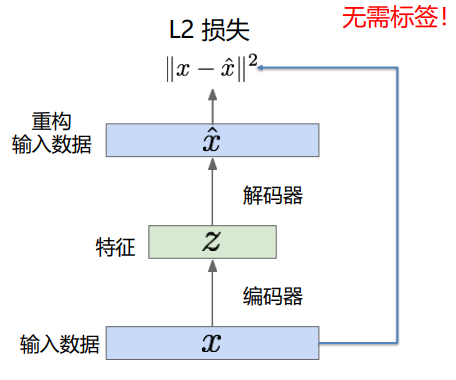自编码器的核心结构 - 基础应用：编码器可提取特征，用于小样本分类任务；解码器可尝试图像生成，从编码空间采样 z 生成图像；
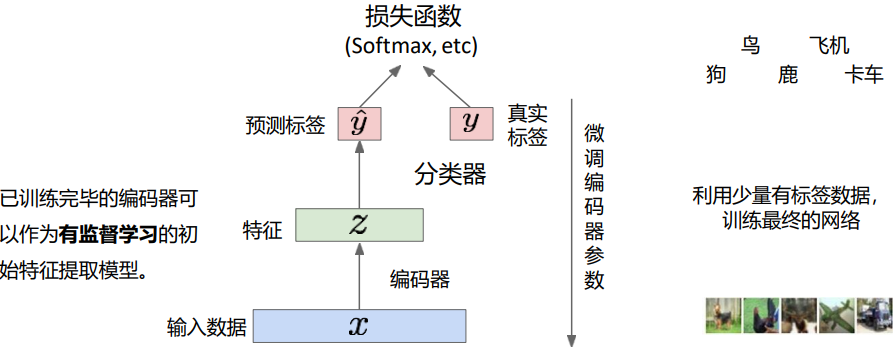编码器提取特征用于分类
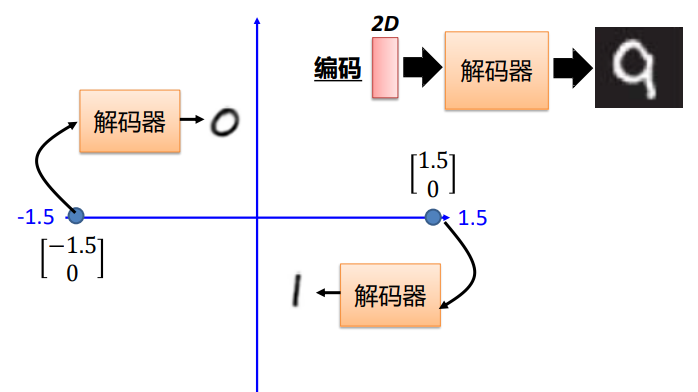编码器提取图像特征，解码器生成图像
解码器生成图像
解码器生成图像
- 核心局限：编码空间的泛化能力极差，神经网络仅稀疏记录训练过的 z 与图像的对应关系，未在训练中出现的 z 无法生成有效图像内容。
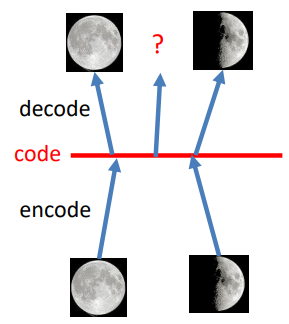自编码器的缺陷：泛化能力差
五、VAE 核心设计：从确定编码到概率分布的关键改进
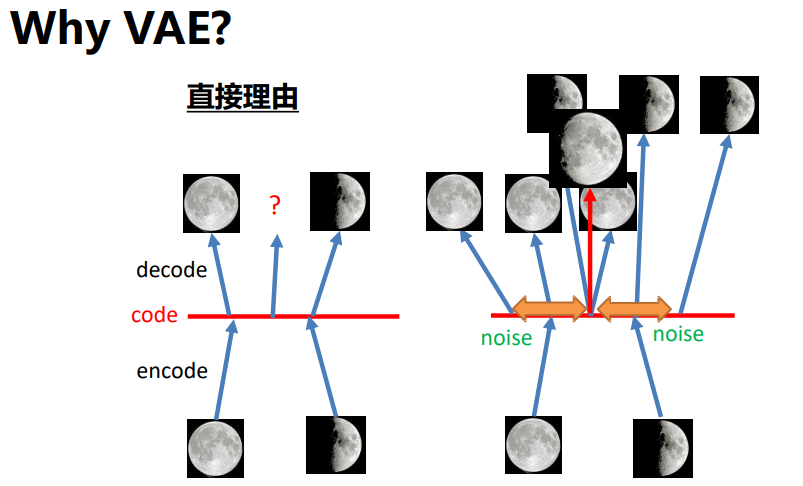VAE解决了自编码器的泛化问题
VAE 是显式密度估计中分布方程需近似求解的典型，核心改进是将自编码器的确定编码改为概率编码，彻底解决了自编码器的泛化问题：
- 编码方式改进 ：编码器不再直接输出确定的编码 z，而是输出 z 的高斯分布均值和方差，从该分布中采样带噪声的 z 输入解码器，通过指数操作保证标准差为正数；
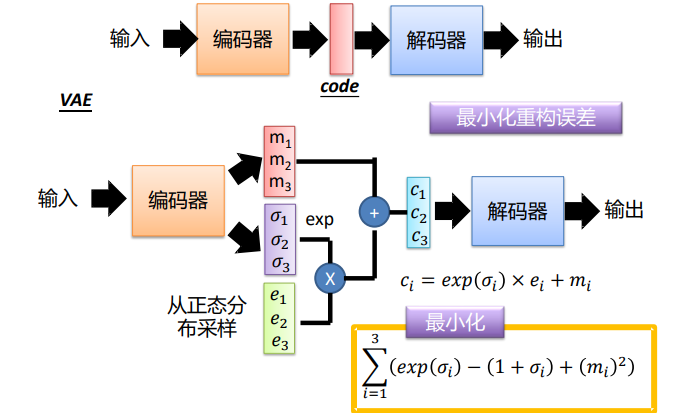自编码器编码方式（上） 与 VAE编码方式（下） 的 对比 - 与高斯混合模型关联 ：高斯混合模型用有限个高斯组件拟合数据分布，VAE 则用无限个高斯组件逼近真实数据分布，且编码 z 的每一维可对应图像的一个属性，调整 z 的不同维度可控制生成图像的对应特征。
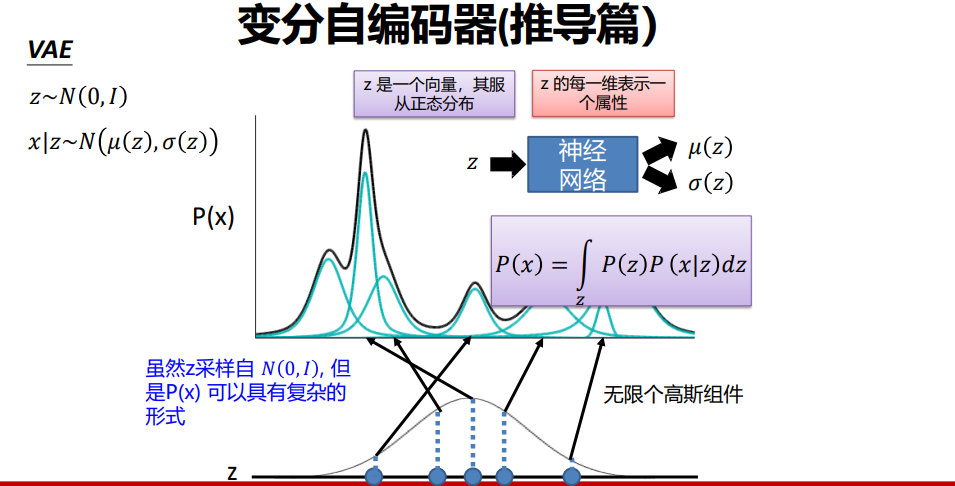VAE与高斯混合模型关联
六、VAE 训练：双损失函数与对数似然下界优化
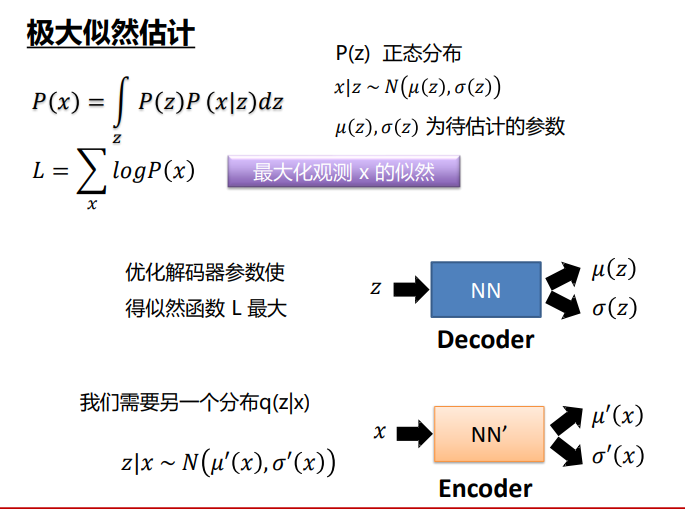VAE 无法直接最大化观测数据对数似然
VAE 无法直接最大化观测数据的对数似然（因隐变量 z 存在，难以完成积分操作），因此采用近似求解的方式，核心是双损失函数设计与对数似然下界优化：
- 双损失函数：一是重构损失，即输入 x 与重构 x 的 L2 损失，保证解码器的重构效果；二是 KL 散度损失，约束编码器输出的高斯分布逼近零均值、一方差的标准正态分布，避免模型退化为普通自编码器；
- 对数似然下界（ELBO）优化：引入分布 q (z|x) 逼近真实的后验分布 p (z|x)，转而优化对数似然的下界，该下界可直接分解为重构项和 KL 散度项，成为 VAE 的实际优化目标。
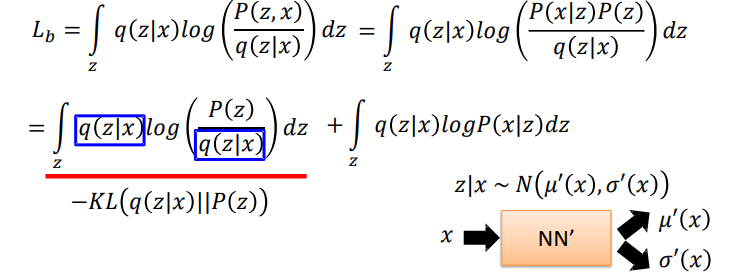双损失函数的数学理论源头
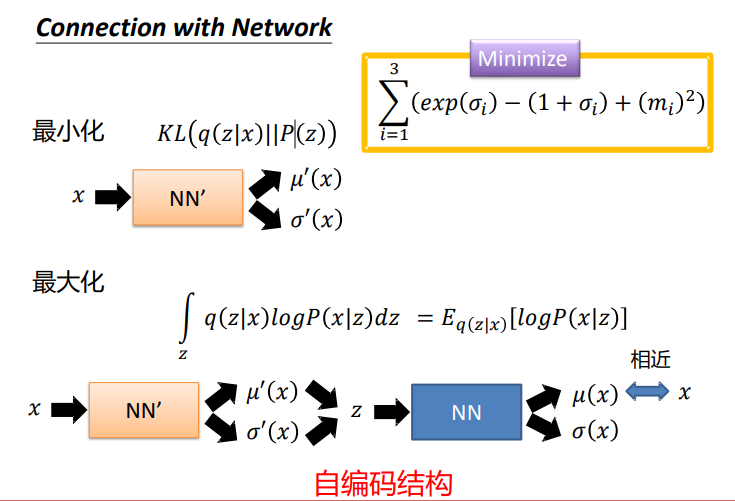KL损失与网络
七、VAE 特性：模型优势、局限与应用特点
VAE 作为生成模型的主流方向之一，其模型使用方式、核心优势与局限性十分鲜明：
- 模型使用：训练完成后可丢弃编码器，直接从标准正态分布中采样 z，输入解码器即可生成新图像；
- 核心优势：能得到编码 z 的概率分布，泛化能力强，可应用于多种生成相关任务；
- 主要局限：仅优化对数似然下界而非真实的对数似然，模型评估难度大，且生成的图像质量相较于 GAN 偏低。
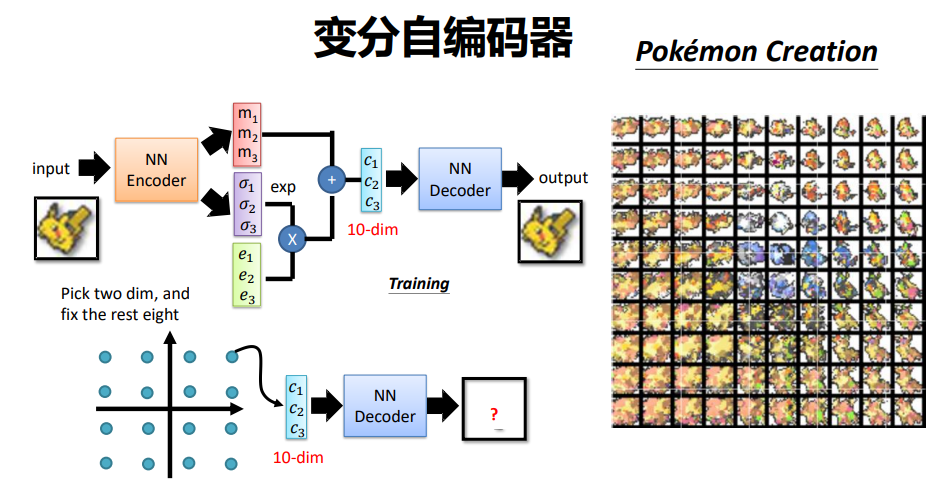利用VAE实现宝可梦生成
利用VAE生成的图像
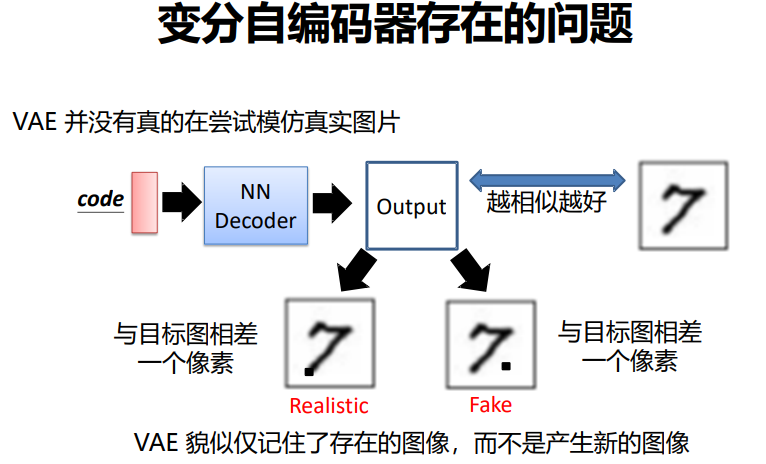VAE的问题
八、学习感悟：生成模型的设计思路与核心逻辑
- 生成模型的设计始终围绕密度估计展开，显式与隐式、可解与近似解的分类，本质是密度估计的不同实现方式；
- VAE 的核心创新是概率思维的引入，将自编码器的确定编码改为概率编码，通过高斯分布采样实现了编码空间的泛化，这是解决自编码器局限的关键；
- 损失函数的设计是模型优化的核心，VAE 的双损失函数实现了重构效果 与分布约束的权衡，避免了模型退化，这种权衡思维是深度学习模型设计的重要思路；
- 不同生成模型各有优劣，PixelRNN/CNN 胜在显式概率可计算，VAE 胜在泛化能力，而后续 GAN 的优势则在生成效果，需根据实际场景选择。
VAE总结
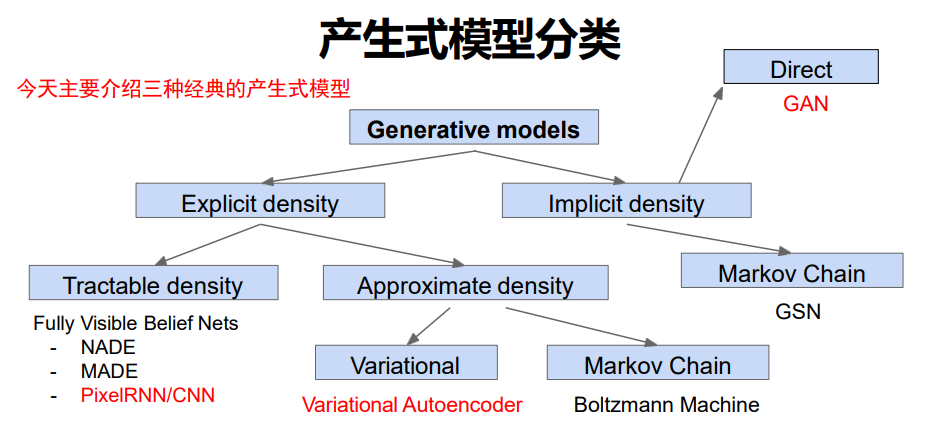产生式模型分类
九、结语
本节课以无监督学习为切入点，厘清了生成模型以密度估计为核心的本质，先剖析了显式可解的 PixelRNN/CNN 的序列生成逻辑，再从自编码器的结构与局限出发，层层深入讲解了 VAE 的概率编码改进、双损失函数设计与对数似然下界优化。VAE 作为显式密度估计中近似求解的典型模型，通过概率思维的引入解决了自编码器的泛化问题，完整呈现了显式生成模型的建模与训练思路，也为后续学习隐式生成模型 GAN 奠定了重要的理论基础。理解密度估计的不同实现方式，以及各类生成模型的设计取舍，是掌握生成模型的核心关键。