【深度学习教程——05_生成模型(Generative)】25_扩散模型为什么能生成高质量图像？Diffusion数学推导

25_扩散模型为什么能生成高质量图像？Diffusion数学推导

本章目标 ：理解 Diffusion Model (扩散模型) 的物理直觉。为什么把一张图慢慢加噪变成雪花点，再反过来去噪，就能生成艺术画？Stable Diffusion 和 Midjourney 背后的魔法到底是什么？

[从 GAN 到 Diffusion：生成模型的范式转移](#从 GAN 到 Diffusion：生成模型的范式转移)
直觉：米开朗基罗的雕刻术
[前向过程 (Forward)：毁图不倦](#前向过程 (Forward)：毁图不倦)
[逆向过程 (Reverse)：起死回生](#逆向过程 (Reverse)：起死回生)
[实战：PyTorch 实现微型 DDPM](#实战：PyTorch 实现微型 DDPM)

1. 从 GAN 到 Diffusion：生成模型的范式转移

GAN (生成对抗网络) ：两个网络打架。优点是生成快，缺点是训练极不稳定（模式崩塌）。
VAE (变分自编码器) ：学分布。优点是数学严谨，缺点是生成的图模糊。
Diffusion (扩散模型)：分解步骤。不要试图一口气画出一张画，而是从一团乱码里，一点点把"不属于画"的杂质去掉。

优势：训练极其稳定（本质上是回归问题 MSE Loss），生成质量极高。
劣势：生成速度慢（需要迭代几十次甚至上千次）。

2. 直觉：米开朗基罗的雕刻术

米开朗基罗曾说："大卫像本来就在这块石头里，我只是把多余的部分去掉了（去噪）。"

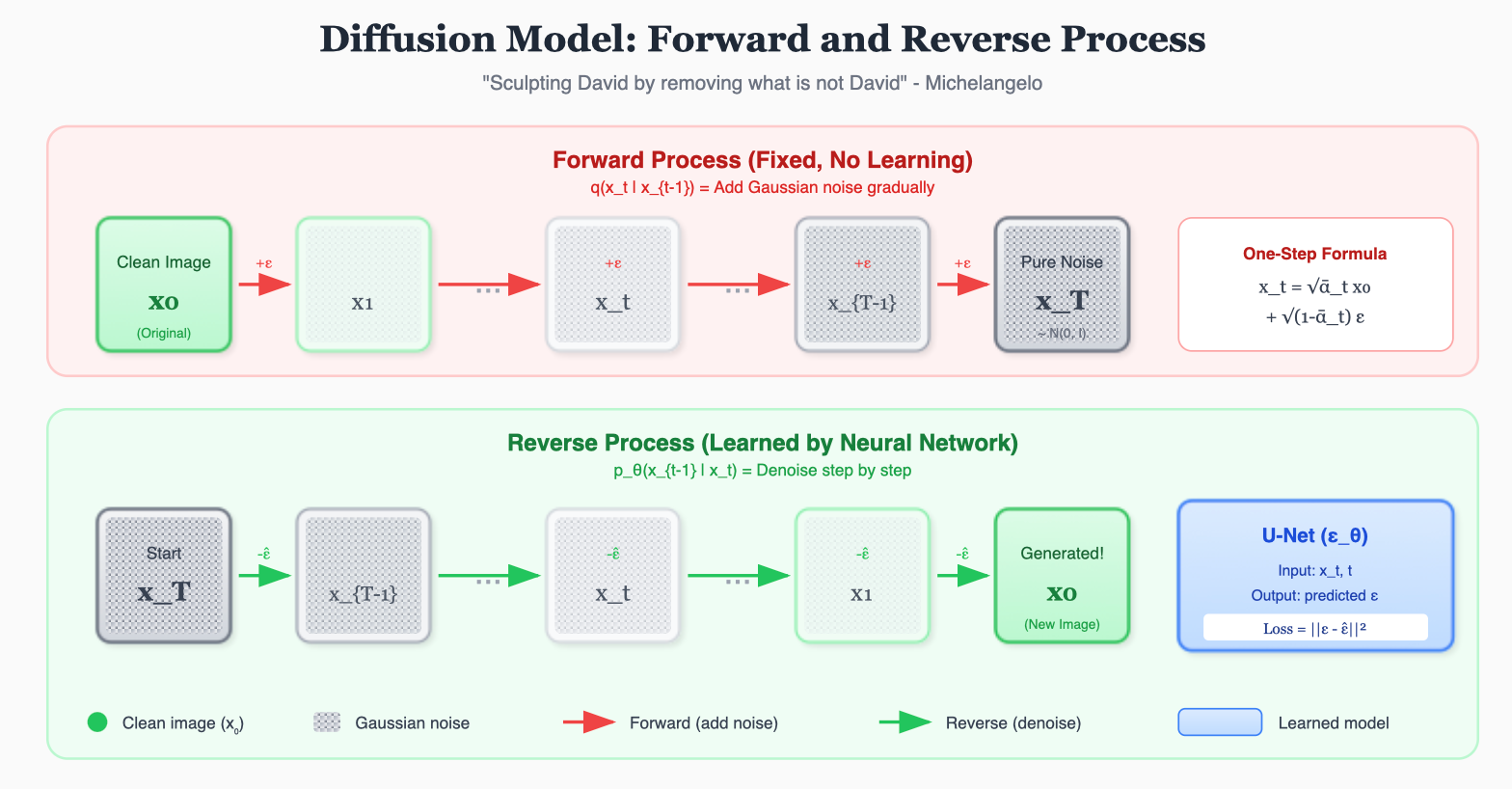
前向 (Forward): 往大卫像上撒灰尘，直到它完全变成一堆灰 (高斯噪声)。这个过程是固定的，不需要学习。
逆向 (Reverse) : 训练一个 AI (U-Net)，让它学会如果我给你一堆灰，你应该吹掉哪一点点灰，能让它更像大卫？
生成: 给 AI 一堆随机的灰，让它吹 1000 次，大卫像就诞生了。

3. 前向过程 (Forward)：毁图不倦

这是一个马尔可夫链 (Markov Chain) 。

我们在每一步给图像 x t − 1 x_{t-1} xt−1 加入少量高斯噪声，得到 x t x_t xt。

x t = 1 − β t x t − 1 + β t ϵ , ϵ ∼ N ( 0 , 1 ) x_t = \sqrt{1-\beta_t} x_{t-1} + \sqrt{\beta_t} \epsilon, \quad \epsilon \sim N(0, 1) xt=1−βt xt−1+βt ϵ,ϵ∼N(0,1)

β t ∈ ( 0 , 1 ) \beta_t \in (0, 1) βt∈(0,1)：噪声强度表 (Schedule)。通常 β t \beta_t βt 随 t t t 增大。

一步到位公式 (很关键！) ：

我们不需要一步步算。利用高斯分布的性质，我们可以直接从 x 0 x_0 x0 算出任意时刻 t t t 的 x t x_t xt（这就是 Re-parameterization 的威力）：

x t = α ˉ t x 0 + 1 − α ˉ t ϵ x_t = \sqrt{\bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon xt=αˉt x0+1−αˉt ϵ

其中 α t = 1 − β t \alpha_t = 1 - \beta_t αt=1−βt， α ˉ t \bar{\alpha}_t αˉt 是 α \alpha α 的累乘。这意味着训练时我们可以随机采样任意时刻进行并行训练！

4. 逆向过程 (Reverse)：起死回生

如果我们能算出后验概率 q ( x t − 1 ∣ x t ) q(x_{t-1}|x_t) q(xt−1∣xt)，那我们就能从噪声 x T x_T xT 一步步还原出 x 0 x_0 x0。

但这个分布太复杂了。

所以我们训练一个神经网络（通常是 U-Net ），来估计这个分布。

具体来说，由 DDPM 论文推导，预测均值等价于预测噪音。

网络输入：

当前时刻的图 x t x_t xt (噪声图)。
当前时刻 t t t (告诉网络现在是第几步，因为第 1000 步和第 1 步的去噪策略完全不同)。

网络输出：

预测的噪音 ϵ θ ( x t , t ) \epsilon_\theta(x_t, t) ϵθ(xt,t)。

训练目标 (Loss) ：
L o s s = ∣ ∣ ϵ − ϵ θ ( x t , t ) ∣ ∣ 2 Loss = ||\epsilon - \epsilon_\theta(x_t, t)||^2 Loss=∣∣ϵ−ϵθ(xt,t)∣∣2

这就是简单的 MSE Loss！

ϵ \epsilon ϵ: 我们自己加的真实噪声（Ground Truth）。
ϵ θ \epsilon_\theta ϵθ: 网络猜的噪声。

5. 实战：PyTorch 实现微型 DDPM

这里展示核心的加噪和采样逻辑。

python 复制代码

import torch
import torch.nn as nn

class DiffusionModel(nn.Module):
    def __init__(self, timesteps=1000):
        super().__init__()
        self.timesteps = timesteps

        # 定义 beta schedule (线性增长)
        self.beta = torch.linspace(1e-4, 0.02, timesteps)
        self.alpha = 1. - self.beta
        # alpha_hat (累乘)
        self.alpha_hat = torch.cumprod(self.alpha, dim=0)

    # 1. 前向加噪 (Forward) -> 得到 x_t 和真实噪声 epsilon
    def noise_images(self, x_0, t):
        # x_0: [b, c, h, w]
        # t: [b] (每个样本随机选一个时间步)
        sqrt_alpha_hat = torch.sqrt(self.alpha_hat[t])[:, None, None, None]
        sqrt_one_minus_alpha_hat = torch.sqrt(1 - self.alpha_hat[t])[:, None, None, None]

        epsilon = torch.randn_like(x_0)

        # x_t = sqrt(alpha_hat) * x_0 + sqrt(1-alpha_hat) * eps
        return sqrt_alpha_hat * x_0 + sqrt_one_minus_alpha_hat * epsilon, epsilon

    # 2. 逆向采样 (Reverse) -> 从 x_T 还原 x_0
    def sample(self, model, n):
        model.eval()
        with torch.no_grad():
            # 从纯噪声开始
            x = torch.randn((n, 3, 64, 64))

            # 从 T 倒数到 1
            for i in reversed(range(1, self.timesteps)):
                t = (torch.ones(n) * i).long()

                # 预测噪声
                predicted_noise = model(x, t)

                # 公式：x_{t-1} = (x_t - ... * predicted_noise) / ... + sigma * z
                # (此处省略繁琐的系数计算代码，核心就是减去预测的噪声)
                alpha = self.alpha[t][:, None, None, None]
                alpha_hat = self.alpha_hat[t][:, None, None, None]
                beta = self.beta[t][:, None, None, None]

                if i > 1:
                    noise = torch.randn_like(x)
                else:
                    noise = torch.zeros_like(x)

                x = 1 / torch.sqrt(alpha) * (x - ((1 - alpha) / (torch.sqrt(1 - alpha_hat))) * predicted_noise) + torch.sqrt(beta) * noise

        model.train()
        return x

# 训练伪代码
# model = UNet()
# diffusion = DiffusionModel()
# opt = optimizer(model.parameters())
#
# for imgs in dataloader:
#     t = diffusion.sample_timesteps(imgs.shape[0]) # 随机 t
#     x_t, noise = diffusion.noise_images(imgs, t)  # 加噪
#     predicted_noise = model(x_t, t)               # 预测
#     loss = mse(noise, predicted_noise)            # 算 MSE
#     loss.backward()
#     opt.step()

Part 6 (进阶领域) 开启预告 ：

我们已经掌握了让 AI 看 (CNN/ViT)、读 (RNN/Transformer) 和画 (GAN/Diffusion)。

最后，我们要让 AI 学会玩。

如何训练一个 AI 打通《超级马里奥》？

这就是 强化学习 (Reinforcement Learning)。

下一章：26_AI如何学会玩游戏？深度强化学习DQN入门