深度学习的数学原理（五）—— 非线性与激活函数

本文主要回答一个问题：为什么神经网络必须要有非线性激活函数？

在深度学习入门时，我们总会被一个问题困扰：明明线性变换（z=wx+bz = wx + bz=wx+b）就能完成输入到输出的映射，为什么还要在每一层加入激活函数？激活函数的"非线性"到底是什么意思？没有它，神经网络就不行吗？

本文先从直观角度讲清激活函数如何引入非线性，或者说神经网络为什么离不开非线性，再用简单数学证明线性网络的局限性，最后通过极简代码，直观对比"线性网络"和"带非线性激活的网络"在拟合数据上的巨大差异，彻底搞懂这个入门核心问题。

一、直观理解：什么是"非线性"？激活函数怎么引入它？

我们先抛开神经网络，用生活中的例子理解"线性"和"非线性"的区别，再对应到激活函数上。

1.1 线性 vs 非线性：一句话区分

线性关系：输入和输出是"成比例"的，画在坐标系里是一条直线，比如"y = 2x + 1"------x增加1，y固定增加2，关系固定不变，没有"弯曲"。

非线性关系：输入和输出不成固定比例，画在坐标系里是一条曲线，比如"y = x²"------x从1增加到2，y从1增加到4；x从2增加到3，y从4增加到9，变化幅度一直在变，有"弯曲"。

简单说：线性是一成不变的比例关系，非线性是灵活变化的关系，而我们现实世界中的数据（比如房价和面积的关系、图片中像素和物体类别的关系），几乎都是非线性的。

1.2 激活函数：给神经网络加弯曲的能力

神经网络的每一层，本质是先做线性变换：z=wx+bz = wx + bz=wx+b（w是权重，b是偏置，x是输入），再通过激活函数输出：a=f(z)a = f(z)a=f(z)（a是当前层的最终输出）。

激活函数的核心作用，就是通过自身的"非线性特性"，把线性变换的输出z，映射成非线性的a------相当于给原本"笔直"的线性关系，加了一个"弯曲"，让网络能学习到数据中的非线性规律。

举个最直观的例子：Sigmoid激活函数

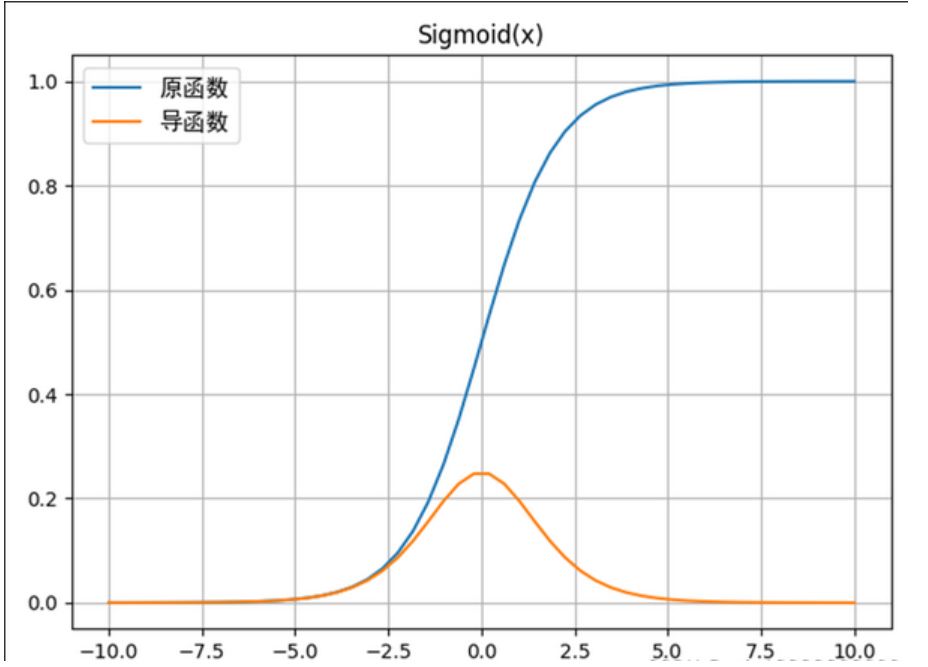
Sigmoid函数的表达式：f(z)=11+e−zf(z) = \frac{1}{1 + e^{-z}}f(z)=1+e−z1它的图像是一条"S型曲线"（非线性），而不是直线。

假设我们有一个简单的输入x=1，线性变换z=0.5x+0（w=0.5，b=0），得到z=0.5；经过Sigmoid激活后，a=f(0.5)≈0.6225------这个映射过程，不是z乘以某个固定系数，而是通过曲线映射得到的，这就是激活函数引入非线性的过程。

如果没有激活函数（相当于f(z)=z，线性激活），那么a=z=0.5，输入和输出依然是线性关系，网络就没有弯曲的能力。

1.3 神经网络为什么需要非线性激活？

答案很简单：没有非线性激活函数，无论神经网络有多少层，本质上都和"单层线性网络"没有区别，无法拟合非线性数据。

举个极端例子：假设我们有一个3层的线性网络（没有激活函数），每层都是线性变换：

第1层：z1=w1x+b1z_1 = w_1 x + b_1z1=w1x+b1，输出a1=z1a_1 = z_1a1=z1（无激活）

第2层：z2=w2a1+b2=w2(w1x+b1)+b2=(w2w1)x+(w2b1+b2)z_2 = w_2 a_1 + b_2 = w_2(w_1 x + b_1) + b_2 = (w_2 w_1)x + (w_2 b_1 + b_2)z2=w2a1+b2=w2(w1x+b1)+b2=(w2w1)x+(w2b1+b2)

第3层：z3=w3a2+b3=w3[(w2w1)x+(w2b1+b2)]+b3=(w3w2w1)x+(w3w2b1+w3b2+b3)z_3 = w_3 a_2 + b_3 = w_3[(w_2 w_1)x + (w_2 b_1 + b_2)] + b_3 = (w_3 w_2 w_1)x + (w_3 w_2 b_1 + w_3 b_2 + b_3)z3=w3a2+b3=w3[(w2w1)x+(w2b1+b2)]+b3=(w3w2w1)x+(w3w2b1+w3b2+b3)

我们发现：3层线性网络的最终输出，依然是"y = Wx + B"的线性形式（其中W = w3w2w1，B = w3w2b1 + w3b2 + b3），和单层线性网络完全等价。

也就是说：没有非线性激活，层数再多，网络也只能学习线性关系，而现实世界中，几乎所有需要解决的问题（比如用图片像素识别猫和狗、用历史数据预测股价），都不是线性的------这就是神经网络必须要有非线性激活函数的核心原因。

二、证明：无激活函数的深层网络 ≡ 单层线性网络

上面的直观例子，我们可以用更通用的数学方法证明，核心是多层线性变换的叠加，依然是线性变换。

证明前提

假设我们有一个L层的神经网络，无任何激活函数，即每一层的输出al=zla^l = z^lal=zl（l表示第l层，从1到L）。

其中，第l层的线性变换为：zl=Wlal−1+blz^l = W^l a^{l-1} + b^lzl=Wlal−1+bl

（说明：WlW^lWl是第l层的权重矩阵，blb^lbl是第l层的偏置向量，al−1a^{l-1}al−1是第l-1层的输出，a0=xa^0 = xa0=x是输入数据）

下面用数学归纳法进行证明

1. 当l=1时（第一层）：a1=z1=W1a0+b1=W1x+b1a^1 = z^1 = W^1 a^0 + b^1 = W^1 x + b^1a1=z1=W1a0+b1=W1x+b1，显然是线性变换；

2. 假设当l=k时（第k层），输出aka^kak是x的线性变换，即：ak=W′x+b′a^k = W' x + b'ak=W′x+b′（其中W′W'W′是权重矩阵，b′b'b′是偏置向量，由前k层的W和b叠加得到）；

3. 当l=k+1时（第k+1层）：ak+1=zk+1=Wk+1ak+bk+1a^{k+1} = z^{k+1} = W^{k+1} a^k + b^{k+1}ak+1=zk+1=Wk+1ak+bk+1，将假设的ak=W′x+b′a^k = W' x + b'ak=W′x+b′代入，得到：

ak+1=Wk+1(W′x+b′)+bk+1=(Wk+1W′)x+(Wk+1b′+bk+1)a^{k+1} = W^{k+1}(W' x + b') + b^{k+1} = (W^{k+1} W') x + (W^{k+1} b' + b^{k+1})ak+1=Wk+1(W′x+b′)+bk+1=(Wk+1W′)x+(Wk+1b′+bk+1)

令W′′=Wk+1W′W'' = W^{k+1} W'W′′=Wk+1W′，b′′=Wk+1b′+bk+1b'' = W^{k+1} b' + b^{k+1}b′′=Wk+1b′+bk+1，则ak+1=W′′x+b′′a^{k+1} = W'' x + b''ak+1=W′′x+b′′，依然是x的线性变换。

结论

通过数学归纳法可证：无论多少层的线性网络（无激活函数），其最终输出都等价于单层线性网络的输出，无法学习任何非线性关系。

只有加入非线性激活函数，让每一层的输出al=f(zl)a^l = f(z^l)al=f(zl)（f是非线性函数），才能打破这种等价性，让深层网络的输出成为"多层非线性变换的叠加"，从而具备拟合非线性数据的能力。

三、代码实例：对比线性与非线性网络的拟合能力

我们用最简单的代码，生成一组非线性数据（模拟现实世界中的数据），然后分别用无激活函数的线性网络和带ReLU激活的非线性网络去拟合，对比两者的效果

3.1 环境准备

import torch
import torch.nn as nn
import matplotlib.pyplot as plt

# 设置matplotlib参数
plt.rcParams['figure.figsize'] = (12, 8)
plt.rcParams['font.size'] = 12
plt.style.use('seaborn-v0_8')

# 设置中文字体显示
plt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# 设置随机种子，保证结果可复现
torch.manual_seed(42)

3.2 生成非线性数据

我们生成一组"y = x² + 随机噪声"的数据（典型的非线性关系），作为我们的训练数据：

# 生成输入x：范围[-3, 3]，共100个数据点
x = torch.linspace(-3, 3, 100).unsqueeze(1)  # 形状：(100, 1)，适配网络输入
# 生成非线性输出y：y = x² + 少量噪声（模拟现实数据）
y = x**2 + torch.randn(100, 1) * 0.1  # 加入噪声，让数据更真实

# 可视化数据：能看到明显的曲线（非线性）
plt.scatter(x.numpy(), y.numpy(), s=10, color='blue', label='真实数据（y=x^2+噪声）')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
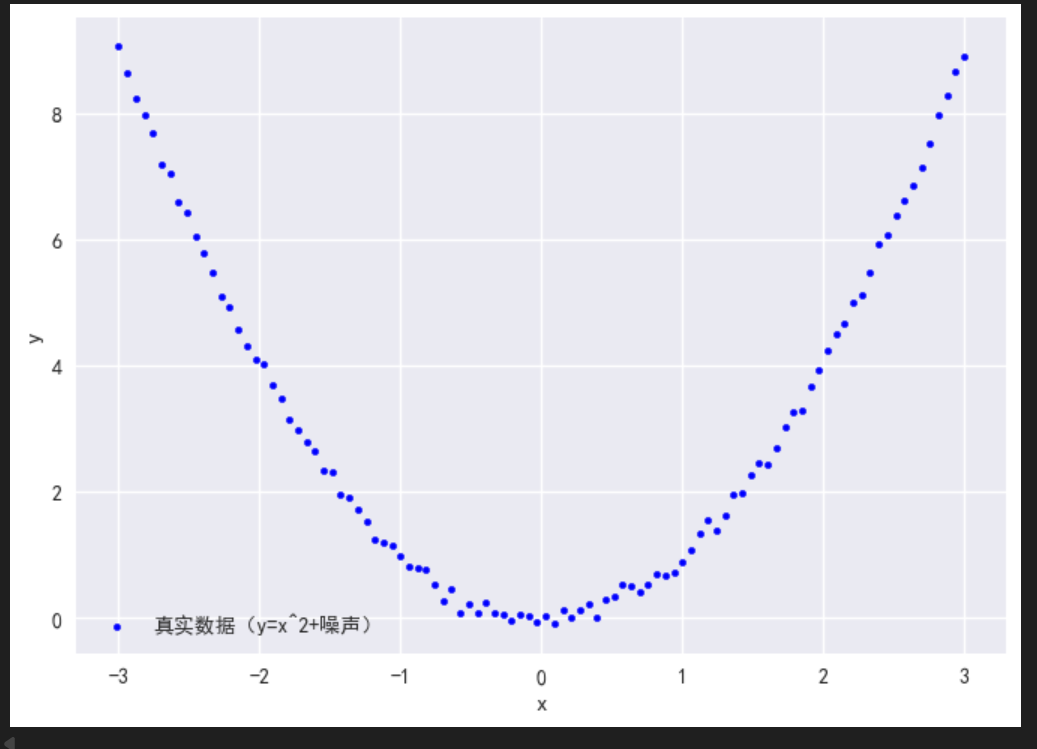
plt.show()

运行代码后，会看到一组呈抛物线分布的蓝色散点------这就是我们要拟合的非线性数据。

3.3 定义两个网络：线性网络 vs 非线性网络

我们定义两个结构完全相同（2层全连接），但是否有激活函数不同的网络：

# 1. 线性网络（无激活函数）
class LinearNetwork(nn.Module):
    def __init__(self):
        super(LinearNetwork, self).__init__()
        # 2层全连接，无任何激活函数
        self.fc1 = nn.Linear(1, 10)  # 输入1维，隐藏层10个神经元
        self.fc2 = nn.Linear(10, 1)  # 隐藏层10个神经元，输出1维
    
    def forward(self, x):
        # 无激活：直接线性变换到底
        z1 = self.fc1(x)
        z2 = self.fc2(z1)
        return z2

# 2. 非线性网络（隐藏层加ReLU激活函数）
class NonLinearNetwork(nn.Module):
    def __init__(self):
        super(NonLinearNetwork, self).__init__()
        self.fc1 = nn.Linear(1, 10)
        self.fc2 = nn.Linear(10, 1)
        self.relu = nn.ReLU()  # 非线性激活函数
    
    def forward(self, x):
        # 线性变换 → ReLU激活 → 再线性变换
        z1 = self.fc1(x)
        a1 = self.relu(z1)  # 关键：加入非线性激活
        z2 = self.fc2(a1)
        return z2

3.4 训练两个网络，对比拟合效果

用相同的优化器、损失函数、训练次数，分别训练两个网络，然后对比它们的拟合结果：

# 初始化网络、优化器、损失函数
linear_net = LinearNetwork()
nonlinear_net = NonLinearNetwork()

# 优化器：随机梯度下降，学习率0.01
optimizer_linear = torch.optim.SGD(linear_net.parameters(), lr=0.01)
optimizer_nonlinear = torch.optim.SGD(nonlinear_net.parameters(), lr=0.01)

# 损失函数：均方误差（回归任务常用）
criterion = nn.MSELoss()

# 训练次数：1000次（足够看到明显差异）
epochs = 1000

for epoch in range(epochs):
    # 训练线性网络
    linear_net.train()
    y_pred_linear = linear_net(x)
    loss_linear = criterion(y_pred_linear, y)
    optimizer_linear.zero_grad()  # 清空梯度
    loss_linear.backward()        # 反向传播
    optimizer_linear.step()       # 更新参数
    
    # 训练非线性网络
    nonlinear_net.train()
    y_pred_nonlinear = nonlinear_net(x)
    loss_nonlinear = criterion(y_pred_nonlinear, y)
    optimizer_nonlinear.zero_grad()
    loss_nonlinear.backward()
    optimizer_nonlinear.step()
    
    # 每200次打印一次损失（看训练进度）
    if (epoch + 1) % 200 == 0:
        print(f"第{epoch+1}次训练：")
        print(f"线性网络损失：{loss_linear.item():.4f}")
        print(f"非线性网络损失：{loss_nonlinear.item():.4f}\n")

3.5 可视化拟合结果

# 关闭训练模式，获取两个网络的预测结果
linear_net.eval()
nonlinear_net.eval()
with torch.no_grad():  # 禁用梯度计算，节省资源
    y_pred_linear = linear_net(x)
    y_pred_nonlinear = nonlinear_net(x)

# 可视化对比
plt.scatter(x.numpy(), y.numpy(), s=10, color='blue', label='真实数据（y=x^2+噪声）')
plt.plot(x.numpy(), y_pred_linear.numpy(), color='red', label='线性网络预测（无激活）')
plt.plot(x.numpy(), y_pred_nonlinear.numpy(), color='green', label='非线性网络预测（ReLU激活）')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.title('线性网络 vs 非线性网络 拟合效果对比')
plt.show()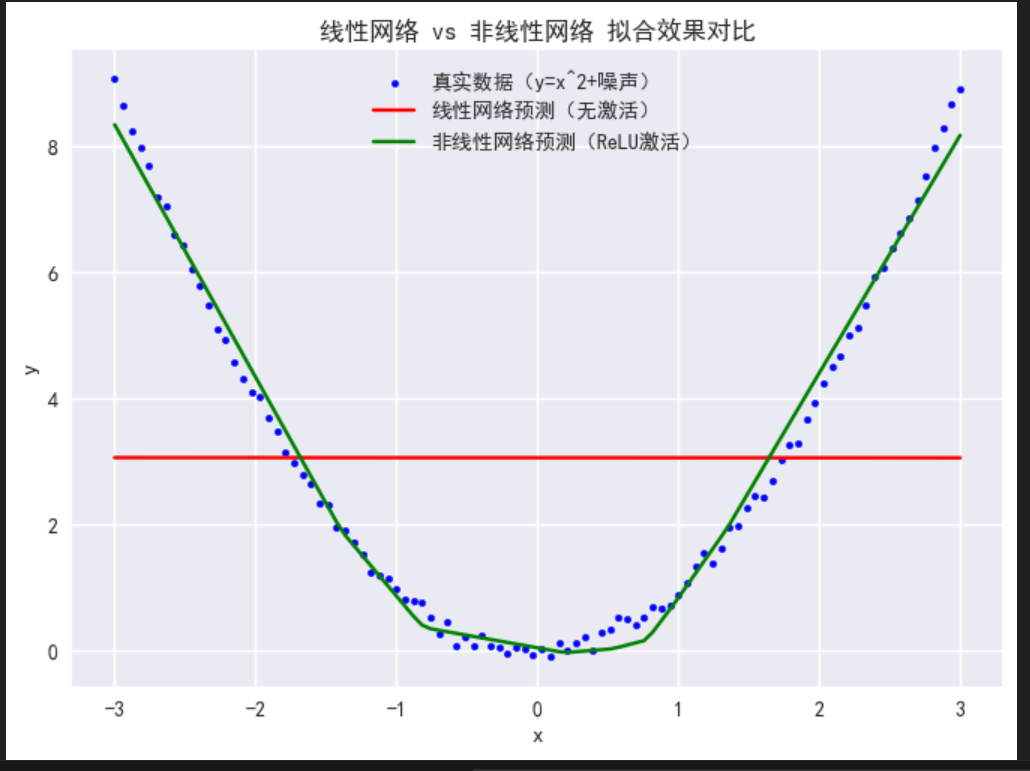

3.6 结果分析

运行代码后，会看到两个明显的差异：

1. 损失差异：训练1000次后，线性网络的损失（约0.5-0.8）远大于非线性网络的损失（约0.01-0.02）------说明非线性网络拟合得更好；

2. 拟合曲线差异：

• 红色曲线（线性网络）：始终是一条直线，无论怎么训练，都只能拟合数据的"整体趋势"，无法贴合抛物线的弯曲部分；

• 绿色曲线（非线性网络）：能明显贴合抛物线的形状，虽然不是完美的x²，但已经能很好地拟合非线性数据的规律。

这就是最直观的证明：线性网络（无激活函数）无法拟合非线性数据，而加入非线性激活函数后，网络就能学习到数据的弯曲规律，拟合效果大幅提升。

四、总结

1. 激活函数通过自身的非线性特性，给神经网络的线性变换"加弯曲"，从而引入非线性；

2. 神经网络需要非线性激活，是因为现实数据大多是非线性的，而无激活的线性网络，无论多少层，都只能拟合线性关系，无法解决实际问题；

3. 数学上可证：多层线性变换叠加 ≡ 单层线性变换；代码上可见：非线性网络的拟合能力远超线性网络。

激活函数是提高神经网络表达能力的至关重要的的一步。简单来说，非线性激活函数，是神经网络从"只能学简单规律"到"能学复杂规律"的关键一步，没有它，就没有深度学习的今天。当然，如何提高表达能力是所有深度学习网络都需要回答的核心问题，能表达多少、表达的好不好，决定了一个网络或者架构的质量。

当然，激活函数的作用远不止如此，下一篇文章我们将讨论激活函数与梯度消失/爆炸之间的关系。