6.3N-Queens -- 回溯法
题目描述
先说一下,这个题目十分之困难。
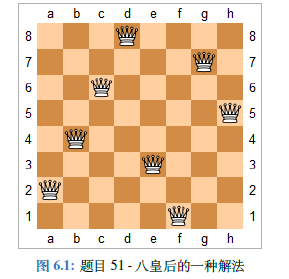
给定一个大小为n的正方形国际象棋棋盘,求有多少种方式可以放置n个皇后,并使得她们互不攻击,即每一行、列、左斜、右斜最多只有一个皇后
输入输出样例
Input :4
Output: [[".Q..", "...Q","Q...","..Q."], // Solution 1
"..Q.", "Q...","...Q",".Q.."\]\] // Solution 2
注:.表示空白位置,Q代表皇后
### 题解
类似于在矩阵中寻找字符串,本体也是通过修改状态矩阵来进行回溯操作,不同的是,我们需要对每一行列,左斜右斜,建立访问数组,来记录他们是否存在皇后。
注意,本题有一个隐藏条件,是满足条件的结果中每一行或列有且仅有一个皇后。这是因为我们一共只有n行n列。所以,**如果我们通过对每一行遍历来插入皇后,我们就不需要对行建立访问数组了。**
这个是缓解这题难度的关键
```cpp
#include
#include
using namespace std;
void backtracking(vector>& ans, vector& board,
vector &column, vector &ldiag, vector &rdiag, int row, int n) {
if (row == n) {
ans.push_back(board);
return;
}
for (int i = 0; i < n; ++i) {
if (column[i] || ldiag[n - row + i - 1] || rdiag[row + i + 1]) {
continue;
}
//修改当前节点状态
board[row][i] = 'Q';
column[i] = ldiag[n - row + i - 1] = rdiag[row + i + 1] = true;
//递归子节点
backtracking(ans, board, column, ldiag, rdiag, row + 1, n);
//回改当前节点状态
board[row][i] = '.';
column[i] = ldiag[n - row + i - 1] = rdiag[row + i + 1] = false;
}
}
vector> solveNQueens(int n) {
vector> ans;
if (n == 0) {
return ans;
}
vector board(n, string(n, '.'));
vector column(n, false), ldiag(2 * n - 1, false), rdiag(2 * n - 1, false);
backtracking(ans, board, column, ldiag, rdiag, 0, n);
return ans;
}
int main() {
int n = 4;
vector> res = solveNQueens(n);
for (int i = 0; i < res.size(); ++i) {
cout << "[";
for (int j = 0; j < res[i].size(); ++j) {
cout << " \"" << res[i][j] << "\"";
if (j != res[i].size() - 1) {
cout << ",";
}
cout << endl;
}
if (i != res.size() - 1) {
cout << " ]," << endl;
}
else {
cout << " ]" << endl;
}
cout << " // Solution " << i + 1 << endl;
}
cout << "]" << endl;
return 0;
}
```
