深度学习框架：Keras

深度学习框架

Keras 是一个模型级（model-level）的库，为开发深度学习模型提供了高层次的构建模块

它不处理张量操作、求微分等低层次的运算。它依赖于一个专门的、高度优化的张量库

来完成这些运算，这个张量库就是 Keras 的后端引擎（backend engine）

Keras 没有选择单个张量库并将 Keras 实现与这个库绑定，而是以模块化的方式处理这个问题

Keras 有三个后端实现：TensorFlow 后端、Theano 后端和微软认知工具包（CNTK，Microsoft cognitive toolkit）后端。

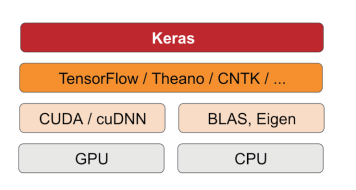
Keras 工作流程：

定义训练数据：输入张量和目标张量
定义层组成的网络（或模型），将输入映射到目标（如下两种方法）
配置学习过程：选择损失函数、优化器和需要监控的指标
调用模型的 fit 方法在训练数据上进行迭代

方法一：使用Sequential类类（仅用于层的线性堆叠，这是目前最常见的网络架构）

python 复制代码

from keras import models
from keras import layers

model = models.Sequential()
model.add(layers.Dense(32,activation='relu',input_shape=(784,)))
model.add(layers.Dense(10,activation='softmax'))

方法二：函数式API（functional API，用于层组成的有向无环图，让你可以构建任意形式的架构）

利用函数式 API，可以操纵模型处理的数据张量，并将层应用于这个张量，就好像这些层是函数一样

python 复制代码

input_tensor = layers.Input(shape=(784,))
x = layers.Dense(32,activation='relu')(input_tensor)
output_tensor = layers.Dense(10,activation='softmax')(x)

model = models.Model(inputs=input_tensor,outputs=output_tensor)

一旦定义好了模型架构，使用 Sequential 模型还是函数式 API 就不重要了

配置学习过程是在编译这一步，需要指定模型使用的优化器和损失函数，以及训练过程中想要监控的指标

下面是单一损失函数的例子

python 复制代码

from keras import optimizers

model.compile(
	optimizer=optimizers.RMSprop(lr=0.001),
	loss='mse',
	metrics=['accuracy']
)

最后，学习过程就是通过 fit() 方法将输入数据的 Numpy 数组（和对应的目标数据）传入模型，这一做法与 Scikit-Learn 及其他机器学习库类似

python 复制代码

model.fit(input_tensor, target_tensor, batch_size=128, epochs=10)

建立深度学习工作站

环境：

在现代 NVIDIA GPU 上运行深度学习实验，某些应用，特别是卷积神经网络的图像处理和循环神经网络的序列处理，在 CPU 上的速度非常之慢，即使是高速多核 CPU 也是如此
如果不想在计算机上安装 GPU，也可以考虑在 AWS EC2 GPU 实例或 Google 云平台上运行深度学习实验。但请注意，时间一长，云端 GPU 实例可能会变得非常昂贵
无论在本地还是在云端运行，最好都使用 UNIX 工作站。虽然从技术上来说可以在 Windows上使用 Keras（Keras 的三个后端都支持 Windows）
使用 Keras 需要安装 TensorFlow、CNTK 或 Theano（如果你希望能够在三个后端之间来回切换，那么可以安装三个）。

运行Keras：两种选择

使用官方的 EC2 深度学习 Amazon 系统映像（AMI），并在 EC2 上以 Jupyter 笔记本的方式运行 Keras 实验。如果你的本地计算机上没有 GPU，你可以选择这种方式。
在本地 UNIX 工作站上从头安装。然后你可以运行本地 Jupyter 笔记本或常规的 Python代码库。如果你已经拥有了高端的 NVIDIA GPU，可以选择这种方式。

场景案例

电影评论分类：二分类问题

将学习根据电影评论的文字内容将其划分为正面或负面

①、数据集

使用 IMDB 数据集，它包含来自互联网电影数据库（IMDB）的 50 000 条严重两极分化的评论。

python 复制代码

from keras.datasets import imdb

# num_words=10000 的意思是仅保留训练数据中前 10 000 个最常出现的单词
(train_data,train_lebels),(test_data,test_labels) = imdb.load_data(num_words=10000)

train_data[0] # [1, 14, 22, 16, ... 178, 32] 单词索引组成的列表
train_labels[0] # 1

max([max(sequence) for sequence in train_data]) # 9999   由于限定为前 10 000 个最常见的单词，单词索引都不会超过 10 000

# 将某条评论迅速解码为英文单词
word_index = imdb.get_word_index() # word_index 是一个将单词映射为整数索引的字典
reverse_word_index = dict(
	[(value,key) for (key,value) in word_index.items()]
)
decoded_review = ''.join(
# 将评论解码。注意，索引减去了 3，因为 0、1、2是为"padding"（填充）、"start of sequence"（序列开始）、"unknown"（未知词）分别保留的索引
	[reverse_word_index.get(i -3,'?') for i in train_data[0]]
)

②、将列表转换为张量（两种方式）

方式一：填充列表

使其具有相同的长度，再将列表转换成形状为 (samples, word_indices)的整数张量，然后网络第一层使用能处理这种整数张量的层

方式二：对列表进行one-hot编码

对列表进行 one-hot 编码，将其转换为 0 和 1 组成的向量。

举个例子，序列 [3, 5] 将会被转换为 10 000 维向量，只有索引为 3 和 5 的元素是 1，其余元素都是 0

然后网络第一层可以用 Dense 层，它能够处理浮点数向量数据

python 复制代码

# 这里采用方式二，进行向量化
import numpy as np
def vectorize_sequences(sequences,dimentsion=10000):
	results = np.zeros((len(sequences),dimension)) # 创建一个形状为（len(sequences),dimension）的零矩阵
	for i,sequence in enumerate(sequences):
		results[i,sequence] = 1 # 将 results[i] 的指定索引设为 1
	return results

x_train = vectorize_sequences(train_data) # 将训练数据序列向量化
x_test = vectorize_sequences(test_data) # 将测试数据序列向量化

x_train[0] # array([ 0., 1., 1., ..., 0., 0., 0.])

# 将标签向量化
y_train = np.asarray(train_labels).astype('float32')
y_test = np.asarray(test_labels).astype('float32')

③、构建网络

输入数据是向量，而标签是标量（1和0），

relu激活函数（也叫非线性）

python 复制代码

from keras import models
from keras import layers

model = models.Sequential()
# 两个中间层，每层都有 16 个隐藏单元
model.add(layers.Dense(16,activation='relu',input_shape=(10000,)))
model.add(layers.Dense(16,activation='relu'))
model.add(layers.Dense(1,activation='sigmoid')) # 第三层输出一个标量，预测当前评论的情感。

网络输出是一个概率值（网络最后一层使用 sigmoid 激活函数，仅包含一个单元），最好使用 binary_crossentropy（二元交叉熵）损失。这并不是唯一可行的选择，比如你还可以使用 mean_squared_error（均方误差）。但对于输出概率值的模型，交叉熵（crossentropy）往往是最好的选择

交叉熵是来自于信息论领域的概念，用于衡量概率分布之间的距离，在这个例子中就是真实分布与预测值之间的距离

④、用rmsprop优化器和binary_crossentropy损失函数配置模型

python 复制代码

# 将优化器、损失函数和指标作为字符串传入，这是因为 rmsprop、binary_crossentropy 和 accuracy 都是 Keras 内置的一部分
model.compile(
	optimizer='rusprop',
	loss='binary_crossentropy',
	metrics=['accuracy']
)

如果希望配置自定义优化器参数，可通过向optimizer参数传入一个优化器类实例来实现

python 复制代码

# 配置优化器
from keras import optimizer

model.compile(
	optimizer=optimizers.RMSprop(lr=0.001),
	loss='binary_crossentropy',
	metrics=['accuracy']
)

自定义的损失函数或指标函数，可以通过向loss和metrics参数传入函数对象来实现

python 复制代码

# 使用自定义的损失和指标
from keras import losses
from keras import metrics

model.compile(
	optimizer=optimizers.RMSprop(lr=0.001),
	loss=losses.binary_crossentropy,
	metrics=[metrics.binary_accuracy]
)

⑤、验证

python 复制代码

# 验证集留出10000个样本
x_val = x_train[:10000]
partial_x_train = x_train[10000:]

y_val = y_train[:10000]
partial_y_train=y_train[10000:]

现在使用 512 个样本组成的小批量，将模型训练 20 个轮次（即对 x_train 和 y_train 两个张量中的所有样本进行 20 次迭代）。

要监控在留出的 10 000 个样本上的损失和精度，将验证数据传入 validation_data 参数来完成

python 复制代码

model.compile(
	optimizer='rmsprop',
	loss='binary_crossentropy',
	metrics=['acc']
)
history = model.fit( # 调用 model.fit() 返回了一个 History 对象是一个字典，包含训练过程中的所有数据
	partial_x_train,
	partial_y_train,
	epochs=20,
	batch_size=512,
	validation_data=(x_val,y_val)
)

history_dict = history.history
history_dict.keys() # dict_keys(['val_acc', 'acc', 'val_loss', 'loss'])

字典中包含 4 个条目，对应训练过程和验证过程中监控的指标

将使用 Matplotlib 在同一张图上绘制训练损失和验证损失，，以及训练精度和验证精度

python 复制代码

# 绘制训练损失和验证损失
import matplotlib.pyplot as plt

history_dict = history.histroy
loss_value = histrory_dict['loss']

epochs = range(1,len(loss_values) + 1)

plt.plot(epochs,loss_values,'bo',label='Training loss') # 'bo' 表示蓝色圆点
plt.plot(epochs,val_loss_values,'b',label='Validation loss') # 'b' 表示蓝色实线
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()

plt.show()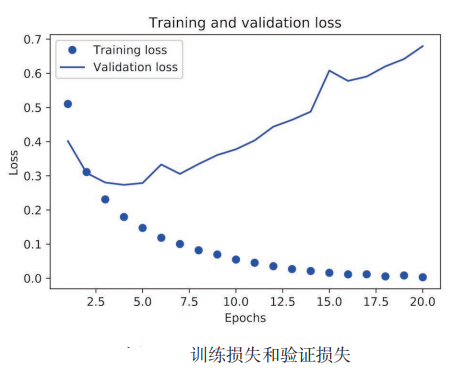

python 复制代码

# 绘制训练精度和验证精度
plt.clf() # 清空图像

acc = histroy_dict['acc']
val_acc = history_dict['val_acc']

plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()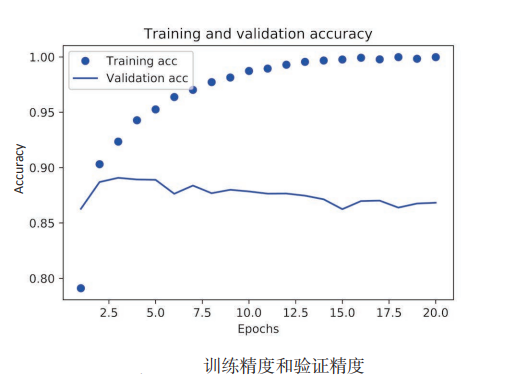

训练损失每轮都在降低，训练精度每轮都在提升。这就是梯度下降优化的预期结果

对于上述的改进点：

上述使用两个隐藏层，可以尝试使用一个或三个隐藏层，观察对验证精度和测试精度的影响
尝试使用更多或更少的隐藏单元，如32个、64个等
尝试使用mse损失函数替代binary_crossentropy
尝试使用tanh激活代替relu

新闻分类：多分类问题

①、加载数据

python 复制代码

# 加载路透社数据集
from keras.datasets import reuters
(train_data,train_labels),(test_data,test_labels) = reuters.load_data(num_words=10000)# 将数据限定为前 10 000 个最常出现的单词

len(train_data) # 8982 训练样本    都是整数列表（单词索引）
len(test_train) # 2246 测试样本

train_data[10] 
"""
每个样本都是整数列表
[1, 245, 273, 207, 156, 53, 74, 160, 26, 14, 46, 296, 26, 39, 74, 2979,
3554, 14, 46, 4689, 4329, 86, 61, 3499, 4795, 14, 61, 451, 4329, 17, 12]
"""

# 用如下代码将索引解码为新闻文本
word_index = reuters.get_word_index()
reverse_word_index = dict([(value, key) for (key, value) in word_index.items()])
"""
索引减去了 3，因为 0、1、2 是为"padding"（填充）、"start of 
sequence"（序列开始）、"unknown"（未知词）分别保留的索引
"""
decoded_newswire = ''.join([reverse_word_index.get(i-3,'?') for i in train_data[0]])

# 样本标签是一个 0~45 范围内的整数，即话题索引编号
 train_labels[10] # 3

②、数据向量化

python 复制代码

# 准备数据，将训练数据和测试数据向量化
import numpy as np

def vectorize_sequences(sequences,dimension=10000):
	results = np.zeros((len(sequences),dimension))
	for i,sequence in enumerate(sequences):
		results[i,sequence] = 1.
	result results

x_train = vectorize_sequences(train_data) 
x_test = vectorize_sequences(test_data)

将标签向量化有两种方法：你可以将标签列表转换为整数张量，或者使用 one-hot 编码。

one-hot 编码是分类数据广泛使用的一种格式，也叫分类编码（categorical encoding）。

在这个例子中，标签的 one-hot 编码就是将每个标签表示为全零向量，只有标签索引对应的元素为 1。

python 复制代码

def to_one_hot(labels,dimension=46):
	results = np.zeros((len(labels),dimension))
	for i,label in enumerate(labels):
		results[i,label] = 1.
	return results

one_hot_train_labels = to_one_hot(train_labels) # 将训练标签向量化
one_hot_test_labels = to_one_hot(test_labels) 

"""
Keras 内置方法可以实现这个操作
from keras.utils.np_utils import to_categorical

one_hot_train_labels = to_categorical(train_labels)
one_hot_test_labels = to_categorical(test_labels)
"""

③、构建网络

输出类别的数量从 2 个变为 46 个

于前面用过的 Dense 层的堆叠，每层只能访问上一层输出的信息。如果某一层丢失了与分类问题相关的一些信息，那么这些信息无法被后面的层找回，也就是说，每一层都可能成为信息瓶颈。

上一个例子使用了 16 维的中间层，但对这个例子来说 16 维空间可能太小了，无法学会区分 46 个不同的类别。这种维度较小的层可能成为信息瓶颈，永久地丢失相关信息。出于这个原因，下面将使用维度更大的层，包含 64 个单元

python 复制代码

from keras import models
from keras import layers

model = models.Sequential()
model.add(layers.Dense(64,activation='relu',input_shape=(10000,)))
model.add(layers.Dense(64,activation='relu'))
model.add(layers.Dense(46,activation='softmax')) #最后一层为46维的输出向量，每个元素（维度）代表不同输出类别

"""
最后一层使用了
softmax激活，网络模型将输出46个不同输出列别上的概率分布
对于每个输入样本，模型都属输出一个46维向量，其中output[i]是样本属于第i个类别的概率，46个概率总和为1
"""
# 最好的损失函数是categorical_crossentropy(分类交叉熵)，用于衡量两个概率分布之间的距离
model.compile(optimizer='rmsprop',loss='categorical_crossentropy',metrics=['accuracy']) #编译模型

④、验证方法

python 复制代码

# 留出验证集
x_val = x_train[:1000]
partial_x_train = x_train[1000:]

y_val = one_hot_train_labels[:1000]
partial_y_train = one_hot_train_labels[1000:]

# 开始训练，共20个轮次
history = model.fit(
	partial_x_train,
	partial_y_train,
	epochs=20,
	batch_size=512,
	validation_data=(x_val,y_val)
)

⑤、绘制损失曲线和精度曲线

python 复制代码

import matplotlib.pyplot as plt

loss = history.history['loss']
val_loss = history.history['val_loss']

epochs = range(1,len(loss) + 1)

plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()


plt.clf() 
acc = history.history['acc']
val_acc = history.history['val_acc']
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()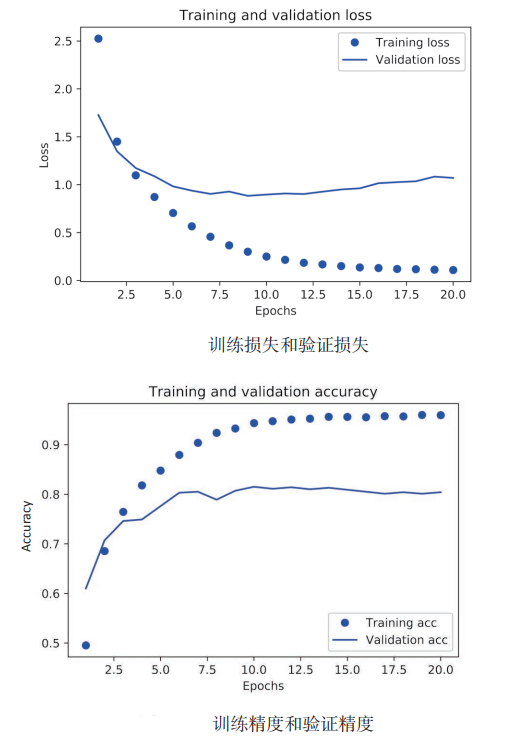

⑥、在新数据上生成预测结果

python 复制代码

predictions = model.predict(x_test) # predictions中每个元素都是长度46的向量
predictions[0].shape # (46,)

# 这个向量所有元素总和为1
np.sum(predications[0]) # 1.0

# 最大的元素就是预测类别，即概率最大的类别
np.argmax(predictions[0]) # 4

处理标签和损失的另一种方法

python 复制代码

model = models.Sequential()
model.add(layers.Dense(64,activation='relu',input_shape=(10000,)))
model.add(layers.Dense(64,activation='relu')) # 如果中间层改为4，模型精度会比前面下降
model.add(layers.Dense(46,activation='softmax'))

model.compile(
	optimizer='rmsprop',
	loss='categorical_crossentropy',# 标签遵循分类编码。对于整数标签，损失函数换成sparse_categorical_crossentropy
	metrics=['accuracy']
)

model.fit(
	partial_x_train,
	partial_y_train,
	epochs=9,
	batch_size=512,
	validation_data=(x_val,y_val)
)

results = model.evaluate(x_test,one_hot_test_labels) # [0.9565213431445807, 0.79697239536954589]

预测房价：回归问题

不要将回归问题与 logistic 回归算法混为一谈。令人困惑的是，logistic 回归不是回归算法，而是分类算法

①、加载数据

python 复制代码

from keras.datasets import boston_housing

(train_data, train_targets), (test_data, test_targets) = boston_housing.load_data()

train_data.shape # (404, 13)  有 404 个训练样本  每个样本都有 13 个数值特征
test_data.shape # (102, 13)   102 个测试样本

train_targets # array([ 15.2, 42.3, 50. ... 19.4, 19.4, 29.1])  房屋价格的中位数，单位是千美元

②、数值准备

取值范围差异很大的数据输入神经网络，是有问题的

所以普遍采用对每个特征进行标准化，对输入数据的每个特征（输入数据矩阵中的列）减去特征平均值，再除以标准差，这样得到的特征平均值为0，标准差为1

python 复制代码

mean = train_data.mean(axis=0) 
train_data -= mean
std = train_data.std(axis=0)
train_data /= std

test_data -= mean
test_data /= std

③、构建网络

python 复制代码

from keras import models
from keras import layers

def build_model():
	model = models.Sequential()
	model.add(layers.Dense(64,activation='relu',input_shape=(train_data.shape[1],)))
	model.add(layers.Dense(64,activation='relu'))
	model.add(layers.Dense(1)) # 网络的最后一层只有一个单元，没有激活，是一个线性层
	model.compile(optimizer='rmsprop',loss='mse',metrics=['mae'])# mse 损失函数，即均方误差预测值与目标值之差的平方。这是回归问题常用的损失函数，训练过程中还监控一个新指标：平均绝对误差。预测值与目标值之差的绝对值。比如，如果这个问题的 MAE 等于 0.5，就表示你预测的房价与实际价格平均相差 500 美元
	return model

④、利用K折验证

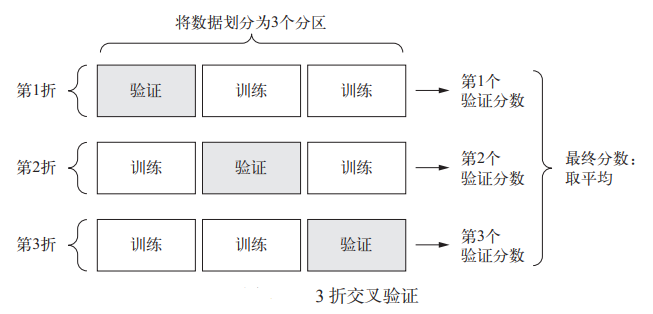
由于划分的训练集和验证集数据点太小，所以验证分数可能会右很大波动。

使用K折交叉，将可用数据划分为K个分区（通常4，或5），实例化K个相同模型，将每个模型在K-1个分区上训练，并在剩下的一个分区进行评估，模型的验证分数等于K个验证分数的平均值

python 复制代码

import numpy as np

k = 4
num_val_samples = len(train_data) // k  # 商的整数部分（向下取整）
num_epochs = 100
all_scores = []

for i in range(k): # 生成从 0 开始到 k-1 的整数序列 即0，1，2，3
	print('processing fold #', i)
	# 准备验证数据：第 k 个分区的数据
	val_data = train_data[i * num_val_samples:(i+1) * num_val_samples]
	val_targets = train_targets[i * num_val_samples:(i+1) * num_val_samples]
	
	# 准备训练数据，其他所有分区的数据
	partial_train_data = np.concatenate(
		[train_data[:i * num_val_samples],train_data[(i + 1) * num_val_samples:]],
		axis=0
	)
	partial_train_targets = np.concatenate(
		[train_target[:i * num_val_samples],train_targets[(i + 1) * num_val_samples]],
		axis=0
	)

	model = build_model() # 构建Keras模型（已编译）
	model.fit(partial_train_data,parial_train_targets,epochs=num_epochs,batch_size=1,verbose=0)
	val_mse,val_mae = model.evaluate(val_data,val_targets,verbose=0)
	all_scores.append(val_mae)

设置num_epochs = 100

python 复制代码

all_scores
# [2.588258957792037, 3.1289568449719116, 3.1856116051248984, 3.0763342615401386]
np.mean(all_scores) # 2.9947904173572462

每次运行模型得到的验证分数有很大差异，从 2.6 到 3.2 不等

平均分数（3.0）是比单一分数更可靠的指标------这就是 K 折交叉验证的关键

在这个例子中，预测的房价与实际价格平均相差 3000 美元，考虑到实际价格范围在 10 000~50 000 美元，这一差别还是很大的。

我们让训练时间更长一点，达到500个轮次，为了记录模型在每轮的表现，需要修改训练循环，以保证每轮的验证分数记录

python 复制代码

num_epochs = 500 
all_mae_histories = [] 
for i in range(k):
	 print('processing fold #', i)
	 val_data = train_data[i * num_val_samples: (i + 1) * num_val_samples] 
	 val_targets = train_targets[i * num_val_samples: (i + 1) * num_val_samples]
	 partial_train_data = np.concatenate( 
	 [train_data[:i * num_val_samples],
	 train_data[(i + 1) * num_val_samples:]], 
	 axis=0)
	 partial_train_targets = np.concatenate(
	 [train_targets[:i * num_val_samples],
	 train_targets[(i + 1) * num_val_samples:]],
	 axis=0)
	 model = build_model() 
	 history = model.fit(partial_train_data, partial_train_targets, 
	 validation_data=(val_data, val_targets),
	 epochs=num_epochs, batch_size=1, verbose=0)
	 mae_history = history.history['val_mean_absolute_error']
	 all_mae_histories.append(mae_history)

# 计算每个轮次中所有折MAE的平均值
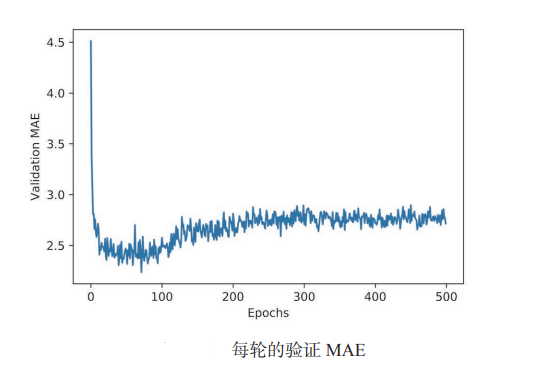
average_mae_history = [np.mean([x[i] for x in all_mae_histories]) for i in range(num_epochs)]

绘制验证分数

python 复制代码

import matplotlib.pyplot as plt
plt.plot(range(1, len(average_mae_history) + 1), average_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()