2026牛客寒假算法基础集训营3（A B G J H F C）

已怯战。😭😭

A 宙天

思路：

x 的范围是 0~100, 所以直接枚举就可以了，也可以自己写个数组毕竟就 2,6,12,20,30,42,56,72,90 这几个数。
代码：

cpp 复制代码

void solve()
{
    int x;
    cin>>x;
    for(int i=1;i<10;i++)
    {
        if(i*(i+1)==x){
            cout<<"YES";
            return;
        }  
    }
    cout<<"NO";
}

B Random

思路：

暴力过了，对于每个 a[i]，去枚举和后面每个数的 gcd。不过其实循环并没有这么大，大约 200 多次就停了。
代码：

cpp 复制代码

void solve()
{
    int n;
    cin>>n;
    for(int i=0;i<n;i++)
    {
        cin>>a[i];
    }
    for(int i=0;i<n;i++)
    {
        for(int j=i+1;j<n;j++)
        {
            if(gcd(a[i],a[j])>1){
                cout<<a[i]<<" "<<a[j]<<endl;
                return;
            }
        }
    }
    cout<<"-1"<<endl;
}

G スピカの天秤

思路：

相等时拿一个就可以，不相等时对数组排序从大的开始拿，直到变换情况。贪心
代码：

cpp 复制代码

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define endl '\n'
#define int long long
const int N=2e5+5;
int a[N];
int b[N];
void solve()
{
    int n,m;
    cin>>n>>m;
    int suml=0,sumr=0;
    for(int i=0;i<n;i++)
    {
        cin>>a[i];
        suml+=a[i];
    }
    for(int i=0;i<m;i++)
    {
        cin>>b[i];
        sumr+=b[i];
    }
    sort(a,a+n);
    sort(b,b+m);
    if(suml==sumr)
    {
        cout<<"1"<<endl;
        return;
    }
    if(suml>sumr){
        int d=suml-sumr;
        int cnt=0;
        for(int i=n-1;i>=0&&d>0;i--)
        {
            d-=a[i];
            cnt++;
        }
        cout<<cnt<<endl;
        return;
    }
    else {
        int d=sumr-suml;
        int cnt=0;
        for(int i=m-1;i>=0&&d>0;i--)
        {
            d-=b[i];
            cnt++;
        }
        cout<<cnt<<endl;
        return;
    }
}
signed main()
{
    IOS
    int t;
    cin>>t;
    while(t--)
    {
        solve();
    }
}

J Branch of Faith

思路：

这个题又恶补了下数据结构的知识，一个完全二叉树的深度计算公式为 ⌊log2(n)⌋+1\lfloor log_2(n) \rfloor+1⌊log2(n)⌋+1，除最后一层外的第 i 层节点数计算公式为 2i−12^{i-1}2i−1，假如当前是在第 H 层那前 H-1 层的节点数为 2H−1+12^{H-1}+12H−1+1。

还是位运算的知识，乘 2k2^k2k 相当于二进制左移 k 位。

这里没有使用 log 函数而是使用 __builtin_clzll(n)，log 可能存在精度问题。

也可以像下面这样算，用位运算求高度。

cpp 复制代码

int h=0;
while((1LL<<h)<=n)h++;

代码：

cpp 复制代码

void solve()
{
    int n,q;
    cin>>n>>q;
    int h=64-__builtin_clzll(n);  
    //int h=log2(n)+1;
    while(q--)
    {
        int x;
        cin>>x;
        int hh=64-__builtin_clzll(x);
        //int hh=log2(x)+1;
        if(hh<h){
            cout<<(1LL<<(hh-1));
        }else cout<<(n-(1LL<<(h-1))+1);
        cout<<endl;
    }          
}

H Tic Tac DREAMIN'

思路：

随便画三个点，然后计算一下面积公式。

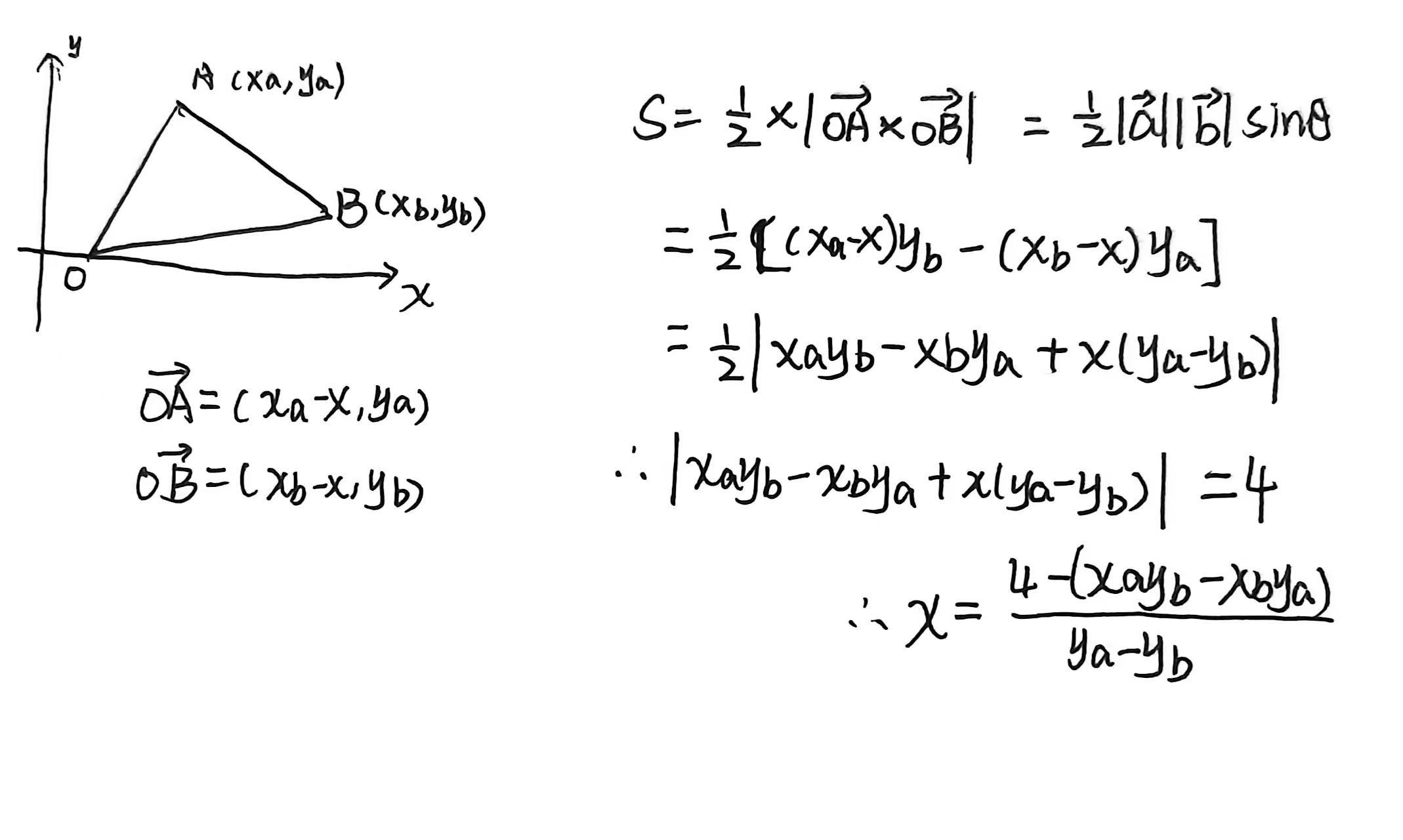
当纵坐标相等时，需要纵坐标为 4。
代码：

cpp 复制代码

void solve()
{
    int x1,x2,y1,y2;
    cin>>x1>>y1>>x2>>y2;
    int m=x1*y2-x2*y1;
    if(y1==y2){
        if(abs(m)==4)cout<<fixed<<setprecision(15)<<1.0<<endl;
        else cout<<"no answer"<<endl;
    }else{
        cout<<fixed<<setprecision(15)<<1.0*(4-m)/(y1-y2);
    }
}

F Energy Synergy Matrix

思路：

额外的步数来自上下换行。

可以根据下面的表格找规律，每五列一个换行。

1,1				紫		红						紫		红
		红						紫		红						紫

代码：

cpp 复制代码

void solve()
{
    int n;
    cin>>n;
    cout<<n-1+n/5<<endl;
}

C Inverted World

思路：

最终结果只能是 01010101010101... 或者 101010101010... 。

分别计算变成这两种目标串所需的操作次数，取最小。

第一种偶数位为 0，奇数位为 1。第二种偶数位为 1，奇数位为 0。

统计错位数，如果之前有一个相反类型的错误，一次操作可以同时修掉这两个。

遍历结束后，剩余未配对的错误只能单独修复，其数量即为最少操作数。
代码：

cpp 复制代码

void solve()
{
    int n;
    cin>>n;
    string s;
    cin>>s;
    int c0=0,c1=0,c2=0,c3=0;
    for(int i=0;i<n;i++)
    {
        if(i%2){
            if(s[i]!='1'){if(c1)c1--;c0++;}//如果存在前一个1->0错误,则将二者配对，用一次操作同时修复，当前这个0->1错误需要被记录
            else{if(c2)c2--;c3++;}
        }else{
            if(s[i]!='0'){if(c0)c0--;c1++;}
            else{if(c3)c3--;c2++;}
        }
    }
    int ans=min(c0+c1,c2+c3);
    cout<<ans<<endl;
}