再来一遍！
在，
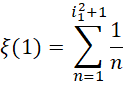
中，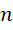
和
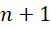之间的1个单位，被平分成
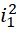份，如果周期是
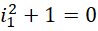，但这个平分的每一份都取边界值的倒数为结果。而在，
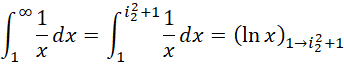
过程中，每一个单位被平分成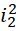
份，周期是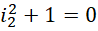
，但是这平分的每一份则取对应数值的倒数为结果。所以，对于积分形式，
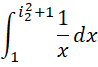
来说，整个区间被分成，
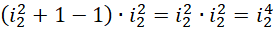
份，每一份的单位是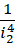
。
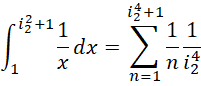
而对于求和形式，
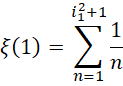
来说，整个区间被分成，
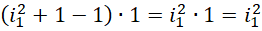
份，每一份的单位都是1。相比较而言，积分形式的对应的求和份数更多，细节更细，
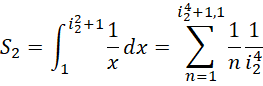
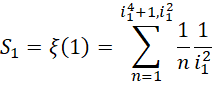
在每个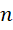
到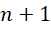
的区间，积分形式为，
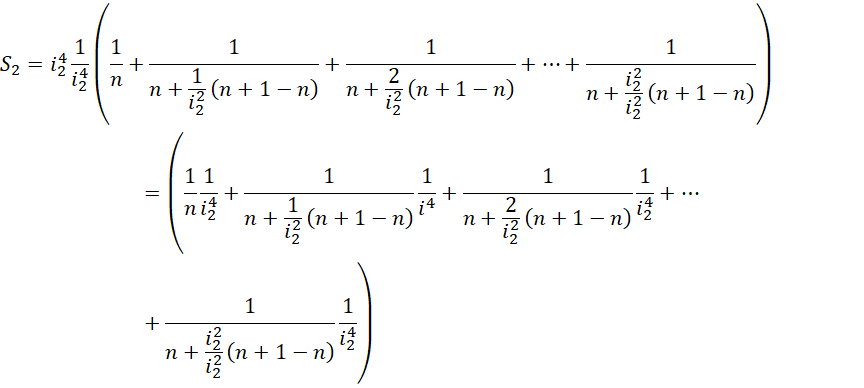
将内部精度提升到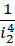
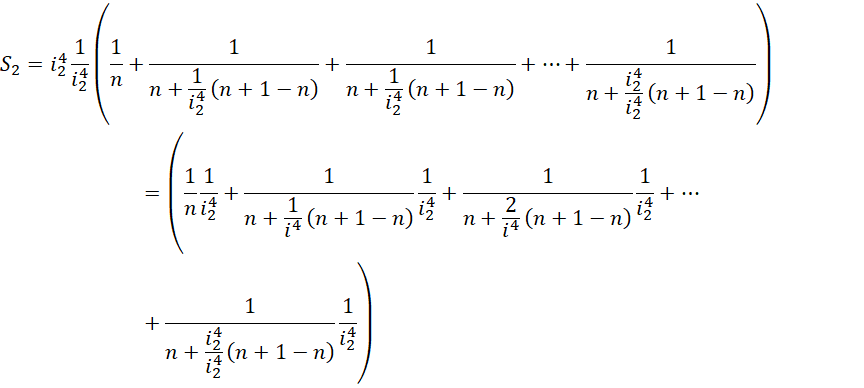
求和形式为，
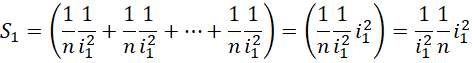
将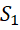
的每个部分都提升精度到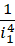
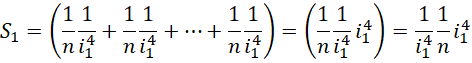
以最高精度计算面积的差值是，
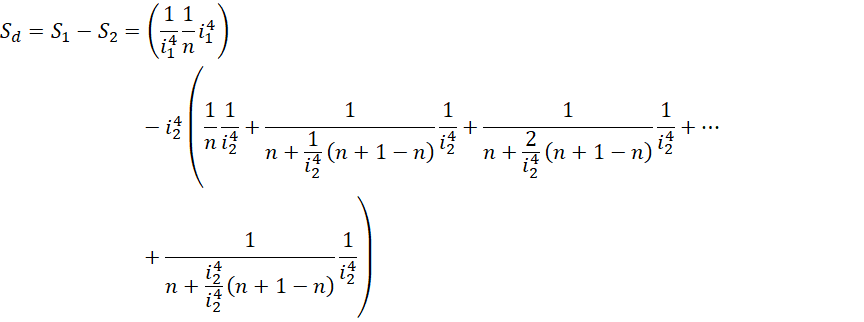
在此处给出比例关系，
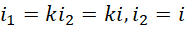
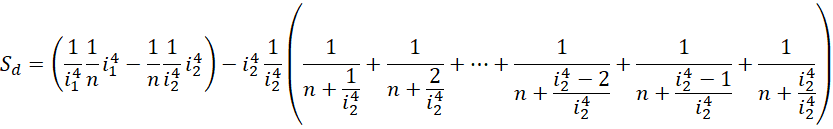
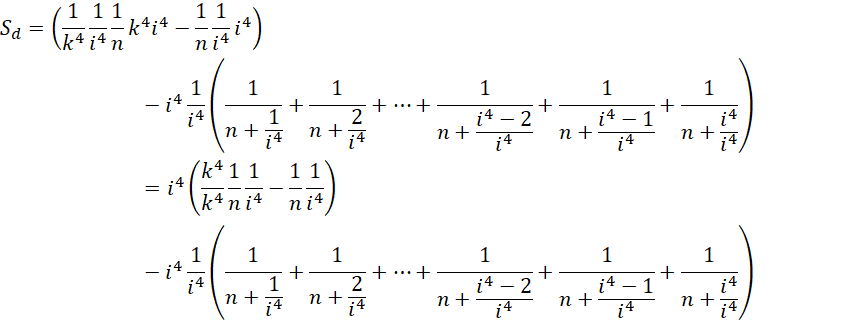
这里出现了，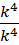
，由于虚数单位自身的可变性，
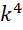和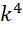
可能完全不相等，正如，
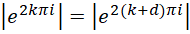
但是作为实际的数值，
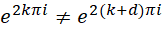
两者相差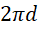
的相位，或者说，不在同一个周期，所以，令，
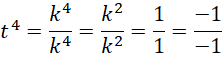
代入每一个微小面积，
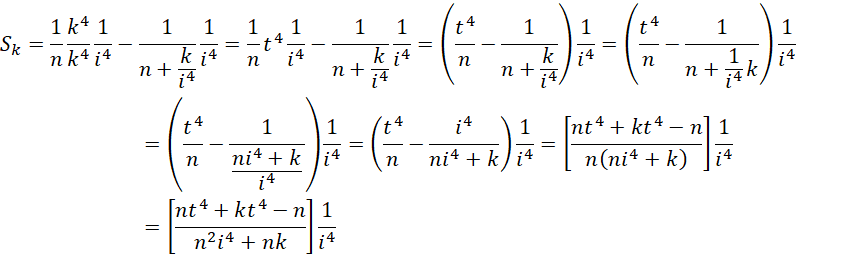
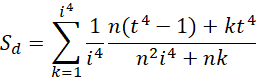
以最高精度计算的总面积差为，
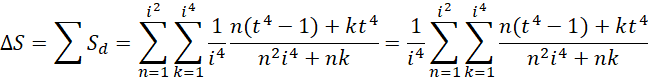
原来的求和公式，
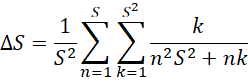
导出积分公式，
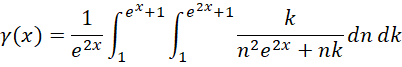
现在的求和公式，
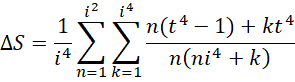
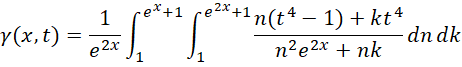
根据的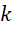
取值，判断，
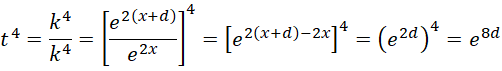
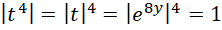
方程变为，
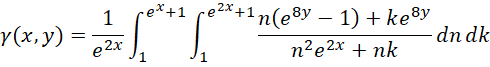
可见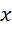
为实数，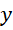
为复数。整数系统和实数系统的单位的关系可以由，
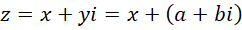
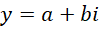
表示。其中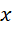
确定大致的比例关系，
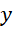用于调整和确定关系的精度。有黎曼泽塔函数可以直到，整数系统的最大值（周期）由其中所有的质数决定，而实数系统则是完全连续的，所以这里用于调整精度的
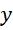就对应了整数系统中的质数分布。这也是黎曼泽塔函数体现质数分布的原因。
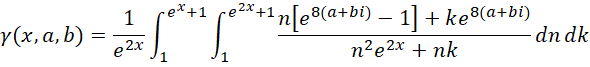
从先前的分析可以看出，如果没有
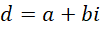
的参与，函数的极值达不到伽马的数值，而且经常是倾斜的，极值最高点并不落在0点上，有微小但难于计算的偏移，所以引入复数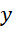
来纠正这种旋转是必须的。但是作为初步极限，我们还是保留
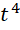在最后再考虑y 
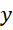的调整。
设，
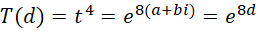
原函数变成，
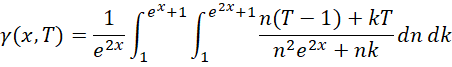
计算，
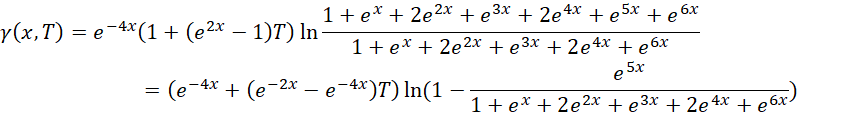
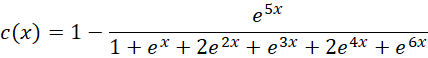
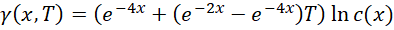
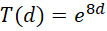
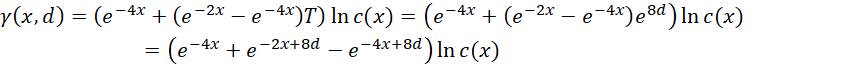
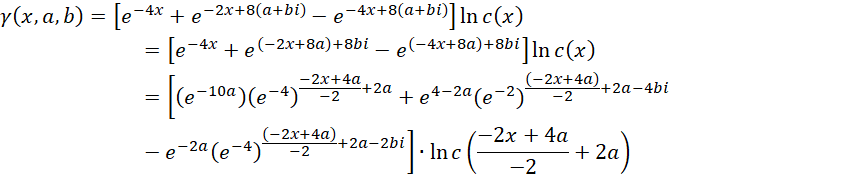
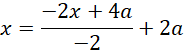
这说明，如果用这种算法，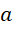
必须分成两个部分，一部分被包含在
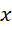里面，另一部被包含在
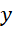里面。为了避免这种情况，我们对内外两层循环都做完整周期的累积。