在前面的七篇文章中,我们逐步拆解了深度学习的核心数学基石:从梯度下降的迭代逻辑、反向传播的链式求导,到激活函数的非线性转换,再到各种优化器对训练效率的提升。我们一直在努力让模型学得更好------尽可能减小训练数据上的误差,但事实上,学得太好反而可能成为模型的致命问题。本文我们就会讨论深度学习中最常见的困境之一:过拟合,以及解决它的核心方法------正则化。
一、过拟合场景
在讲解原理之前,我们先通过一个简单的回归任务,亲手构建一个过拟合模型,直观感受过拟合的表现。
我们的任务是:拟合一组带有噪声的正弦曲线数据。理想情况下,模型应该学习到正弦曲线的整体趋势;但如果模型"过度努力",就会去拟合每一个噪声点,最终失去泛化能力------这就是过拟合。
1.1 代码实现
python
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import TensorDataset, DataLoader, random_split
# 1. 生成带噪声的正弦曲线数据,并转换为PyTorch张量(PyTorch默认使用张量计算)
np.random.seed(42) # 固定随机种子,保证结果可复现
x_np = np.linspace(0, 2*np.pi, 100) # 0到2π之间生成100个均匀分布的点
y_true_np = np.sin(x_np) # 真实的正弦曲线
y_noise_np = y_true_np + 0.1 * np.random.randn(100) # 添加高斯噪声,模拟真实数据的扰动
# 转换为PyTorch张量(float32为PyTorch常用数据类型,维度适配:[样本数, 特征数])
x = torch.tensor(x_np, dtype=torch.float32).unsqueeze(1) # 从(100,)转为(100, 1),适配模型输入
y_true = torch.tensor(y_true_np, dtype=torch.float32).unsqueeze(1)
y_noise = torch.tensor(y_noise_np, dtype=torch.float32).unsqueeze(1)
# 2. 划分训练集和验证集(替代TensorFlow的validation_split=0.2)
dataset = TensorDataset(x, y_noise)
train_size = int(0.8 * len(dataset)) # 80%为训练集
val_size = len(dataset) - train_size # 20%为验证集
train_dataset, val_dataset = random_split(dataset, [train_size, val_size])
# 创建DataLoader(批量加载数据,适配PyTorch训练逻辑,对应原batch_size=16)
train_loader = DataLoader(train_dataset, batch_size=16, shuffle=True)
val_loader = DataLoader(val_dataset, batch_size=16, shuffle=False)
# 3. 构建一个"过于复杂"的模型(容易过拟合),沿用原结构(3个隐藏层,每个64神经元)
class OverfitModel(nn.Module):
def __init__(self):
super(OverfitModel, self).__init__()
# 定义网络层,对应原Dense层,relu激活函数
self.fc1 = nn.Linear(1, 64) # 输入维度1,输出维度64(对应原input_shape=(1,))
self.fc2 = nn.Linear(64, 64)
self.fc3 = nn.Linear(64, 64)
self.fc4 = nn.Linear(64, 1) # 输出层:回归任务,无激活函数
self.relu = nn.ReLU() # 激活函数,统一调用
def forward(self, x):
# 前向传播逻辑,对应原模型的顺序计算
x = self.relu(self.fc1(x))
x = self.relu(self.fc2(x))
x = self.relu(self.fc3(x))
x = self.fc4(x)
return x
overfit_model = OverfitModel() # 实例化模型
# 4. 定义优化器和损失函数(对应原compile步骤)
criterion = nn.MSELoss() # 均方误差损失,回归任务常用
optimizer = optim.Adam(overfit_model.parameters(), lr=0.001) # Adam优化器,学习率0.001
# 5. 训练模型(手动实现训练循环,替代原fit方法,故意训练500轮加剧过拟合)
epochs = 500
train_losses = [] # 记录训练损失,用于后续可视化
val_losses = [] # 记录验证损失,用于后续可视化
for epoch in range(epochs):
# 训练阶段
overfit_model.train() # 切换为训练模式
train_loss = 0.0
for inputs, labels in train_loader:
optimizer.zero_grad() # 梯度清零,避免累积(PyTorch核心步骤)
outputs = overfit_model(inputs) # 前向传播
loss = criterion(outputs, labels) # 计算损失
loss.backward() # 反向传播,计算梯度(对应前文反向传播知识)
optimizer.step() # 梯度下降,更新参数(对应前文梯度下降知识)
train_loss += loss.item() * inputs.size(0) # 累积批次损失
# 计算本轮平均训练损失
train_loss_avg = train_loss / len(train_loader.dataset)
train_losses.append(train_loss_avg)
# 验证阶段
overfit_model.eval() # 切换为评估模式,禁止 dropout、批量归一化等干扰
val_loss = 0.0
with torch.no_grad(): # 禁用梯度计算,节省内存、加快速度
for inputs, labels in val_loader:
outputs = overfit_model(inputs)
loss = criterion(outputs, labels)
val_loss += loss.item() * inputs.size(0)
# 计算本轮平均验证损失
val_loss_avg = val_loss / len(val_loader.dataset)
val_losses.append(val_loss_avg)
# 6. 预测并可视化结果(转换为numpy数组,适配matplotlib绘图)
overfit_model.eval()
with torch.no_grad():
y_pred_overfit = overfit_model(x).numpy() # 模型预测
y_true_np = y_true.numpy() # 真实值转为numpy
y_noise_np = y_noise.numpy()# 带噪声数据转为numpy
x_np = x.numpy().squeeze() # 输入x转为numpy,删除多余维度
# 绘制图像(与原图风格、标签一致)
plt.figure(figsize=(10, 6))
plt.scatter(x_np, y_noise_np.squeeze(), color='orange', label='带噪声的训练数据', alpha=0.6)
plt.plot(x_np, y_true_np.squeeze(), color='blue', label='真实正弦曲线', linewidth=2)
plt.plot(x_np, y_pred_overfit.squeeze(), color='red', label='过拟合模型预测曲线', linewidth=2)
plt.xlabel('x')
plt.ylabel('y = sin(x) + 噪声')
plt.title('过拟合现象演示:模型过度拟合噪声点')
plt.legend()
plt.show()
# 输出训练集和验证集的最终损失(与原输出一致)
train_loss_overfit = train_losses[-1]
val_loss_overfit = val_losses[-1]
print(f"过拟合模型 - 训练集损失:{train_loss_overfit:.6f}")
print(f"过拟合模型 - 验证集损失:{val_loss_overfit:.6f}")输出如下
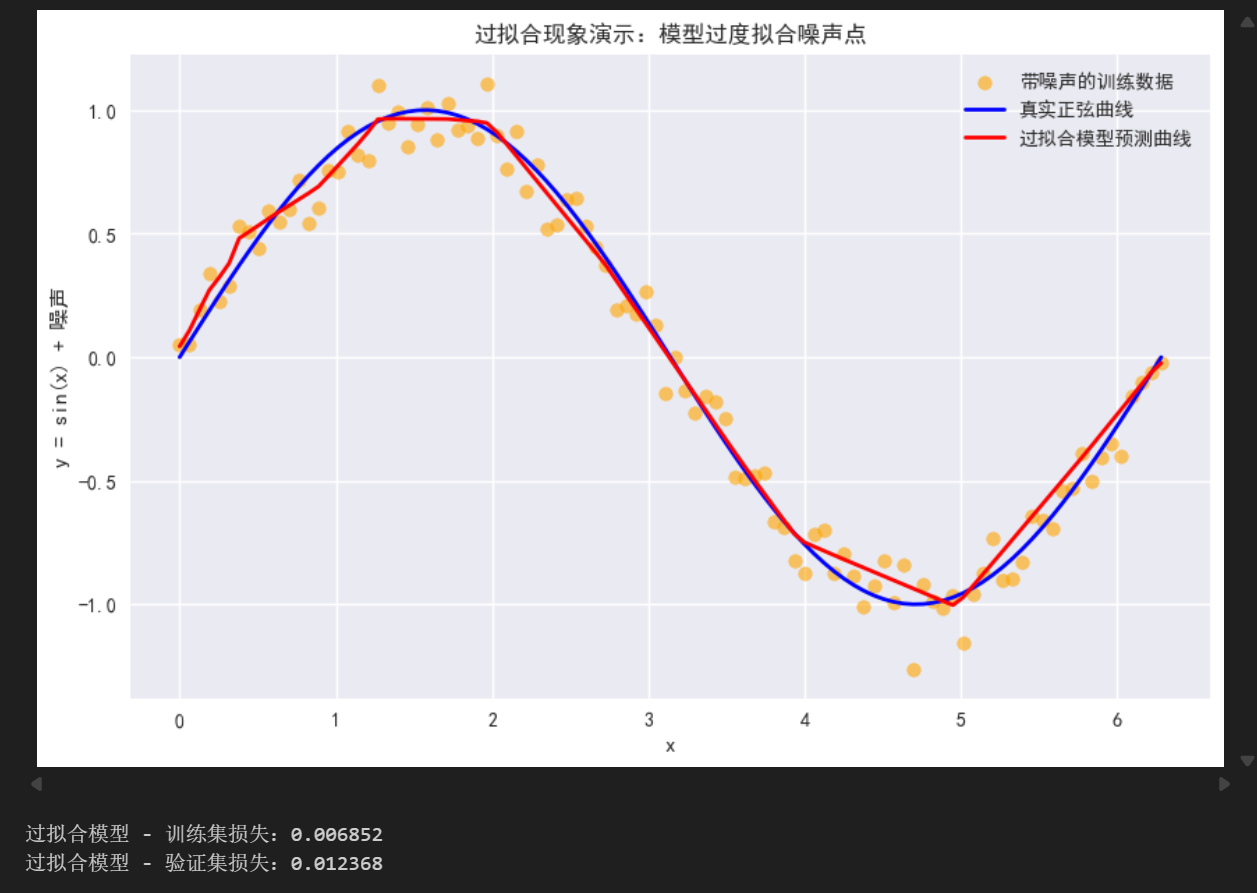
1.2 过拟合的直观表现
运行上述代码后,你会观察到两个关键现象,这也是过拟合的核心特征:
-
训练集损失极低(接近0),但验证集损失很高(几乎是训练集的二倍):模型在训练数据上几乎完美拟合了每一个点(包括我们添加的噪声),但在未见过的验证数据上表现很差;
-
预测曲线"崎岖不平":红色的预测曲线没有贴合蓝色的真实正弦曲线趋势,反而来回波动,试图穿过每一个橙色的噪声点------这就是"过度拟合"的直观体现。
为什么会出现这种情况?我们在前文学习优化器时,强调"最小化训练损失",但显然,仅追求训练损失最小化是不够的。接下来,我们从本质上解析过拟合的原因。
二、过拟合的本质原因:模型过度学习
过拟合的核心定义是:模型在训练数据上表现极好,但在新的、未见过的数据(泛化数据)上表现极差。其本质是模型过度学习了训练数据中的"噪声"和"偶然特征",而忽略了数据背后的"普遍规律"------也就是我们想要模型学习的核心模式。
结合我们前面学过的数学知识,从三个维度拆解过拟合的原因,更易理解:
2.1 模型复杂度 > 数据复杂度
这是过拟合最常见的原因。我们的任务是拟合简单的正弦曲线(1维线性可逼近的非线性关系),但我们构建了包含3个隐藏层、共192个神经元的复杂模型。
从数学角度看,模型的复杂度由其参数数量决定:我们的模型中,每个Dense层的参数包括权重(W)和偏置(b),总参数数量超过1.3万。而我们的训练数据只有100个样本------参数数量远大于样本数量时,模型有足够的"自由度"去"记忆"每一个样本的特征,包括噪声,而不是"学习"规律。
类比来说:用一个100次多项式去拟合10个点,总能找到一条完美穿过所有点的曲线,但这条曲线毫无泛化意义------这就是模型复杂度过高的问题。
2.2 训练数据不足或有噪声
训练数据是模型学习的"素材",如果素材太少、质量太差,模型就会"抓错重点"。
在我们的代码中,虽然有100个样本,但每个样本都添加了噪声(y_noise = y_true + 0.1*随机噪声)。这些噪声是"偶然特征"------不是正弦曲线本身的属性,而是我们模拟的真实数据中的干扰。当模型复杂度过高时,它会把这些噪声当成"普遍规律"去学习,导致泛化能力下降。
2.3 训练轮次过多(过度训练)
在前文学习梯度下降时,我们知道训练的本质是"迭代调整参数,最小化训练损失"。但如果训练轮次过多,模型会在训练数据上不断"微调"参数,直到完全拟合所有样本(包括噪声)。
从优化角度看,这相当于模型收敛到了"训练损失的最小值",但这个最小值对应的参数,并不是"泛化损失最小"的参数------模型在训练数据上"过度收敛",反而偏离了最优的泛化方向。
总结来说:**过拟合的本质,是模型的"拟合能力"超过了数据的"真实规律复杂度",导致模型学习到了无关信息,最终失去泛化能力。**要解决这个问题,核心思路是"约束模型的拟合能力"------正则化就是最常用、最核心的方法。
三、正则化
正则化(Regularization)的核心思想的是:在模型的损失函数中,加入一个"正则项"(也叫惩罚项),约束模型的参数大小,从而降低模型的复杂度,迫使模型放弃"记忆噪声",转而学习数据的核心规律。
这里需要注意:正则化并不会改变模型的结构,也不会改变梯度下降、反向传播的核心逻辑------它只是通过修改"损失函数",改变参数更新的方向,让模型在"拟合训练数据"和"降低复杂度"之间找到平衡。
结合我们前文学习的损失函数知识:假设我们的原始损失函数为L(θ)L(\theta)L(θ)(θ\thetaθ代表模型的所有参数,如权重W和偏置b),加入正则项后,新的损失函数为:
Lreg(θ)=L(θ)+λ⋅R(θ)L_{reg}(\theta) = L(\theta) + \lambda \cdot R(\theta)Lreg(θ)=L(θ)+λ⋅R(θ)
其中:
-
L(θ)L(\theta)L(θ):原始损失函数(如我们代码中用的均方误差MSE,分类任务中用的交叉熵),负责衡量模型在训练数据上的拟合程度;
-
λ\lambdaλ(lambda):正则化强度系数,是一个超参数,由我们手动调整------λ\lambdaλ越大,惩罚越强,模型复杂度越低(但可能欠拟合);λ\lambdaλ越小,惩罚越弱,模型越容易过拟合;
-
R(θ)R(\theta)R(θ):正则项,用于惩罚模型的参数,常用的有两种:L1正则化和L2正则化。
接下来,我们从数学上详细解析这两种最常用的正则化方法,以及它们如何解决过拟合问题。
四、正则化的数学原理:如何约束模型参数?
正则化解决过拟合的核心数学逻辑是:通过惩罚参数的"大小"或"稀疏性",降低模型的"表达能力",让模型无法过度拟合噪声。下面分别讲解L1和L2正则化(重点讲解L2,因为它在深度学习中更常用)。
4.1 L2正则化(权重衰减):最常用的正则化方法
L2正则化的正则项R(θ)R(\theta)R(θ),是模型所有参数(通常只惩罚权重W,不惩罚偏置b,原因下文说明)的平方和,公式如下:
R(θ)=12∑iWi2R(\theta) = \frac{1}{2} \sum_{i} W_i^2R(θ)=21i∑Wi2
其中WiW_iWi代表模型中所有的权重参数(不包含偏置b),乘以1/2是为了后续求导时,平方项的系数能和1/2抵消,简化计算(不影响最终的参数更新趋势)。
加入L2正则化后,完整的损失函数(以回归任务的MSE为例)为:
Lreg(θ)=1N∑n=1N(yn−y^n)2+λ2∑iWi2L_{reg}(\theta) = \frac{1}{N} \sum_{n=1}^N (y_n - \hat{y}n)^2 + \frac{\lambda}{2} \sum{i} W_i^2Lreg(θ)=N1n=1∑N(yn−y^n)2+2λi∑Wi2
其中KaTeX parse error: Can't use function '' in math mode at position 2: N̲是训练样本数量,$y_n是真实标签,y^n\hat{y}_ny^n是模型预测值。
L2正则化解决过拟合的数学逻辑
我们在前文学习梯度下降时,参数更新的核心是"对损失函数求导,然后沿梯度反方向更新参数"。对于L2正则化,我们对新的损失函数Lreg(θ)L_{reg}(\theta)Lreg(θ)求权重W的偏导:
∂Lreg∂W=∂L(θ)∂W+λ⋅W\frac{\partial L_{reg}}{\partial W} = \frac{\partial L(\theta)}{\partial W} + \lambda \cdot W∂W∂Lreg=∂W∂L(θ)+λ⋅W
对应的梯度下降参数更新公式(以单步更新为例)为:
Wnew=Wold−η⋅(∂L(θ)∂W+λ⋅Wold)W_{new} = W_{old} - \eta \cdot \left( \frac{\partial L(\theta)}{\partial W} + \lambda \cdot W_{old} \right)Wnew=Wold−η⋅(∂W∂L(θ)+λ⋅Wold)
整理后可得:
Wnew=Wold⋅(1−η⋅λ)−η⋅∂L(θ)∂WW_{new} = W_{old} \cdot (1 - \eta \cdot \lambda) - \eta \cdot \frac{\partial L(\theta)}{\partial W}Wnew=Wold⋅(1−η⋅λ)−η⋅∂W∂L(θ)
这里的关键的是(1−η⋅λ)(1 - \eta \cdot \lambda)(1−η⋅λ)这一项------由于学习率η\etaη和正则化强度λ\lambdaλ都是正数,所以(1−η⋅λ)(1 - \eta \cdot \lambda)(1−η⋅λ)是一个小于1的数。这意味着,每次更新权重时,都会先将权重W乘以一个小于1的系数,再进行梯度更新------本质是"缩小权重",这也是L2正则化被称为"权重衰减"的原因。
为什么缩小权重能解决过拟合?
从模型表达能力来看,权重W的绝对值越大,模型的拟合能力越强(比如,权重越大,某一特征对输出的影响就越大)。L2正则化通过惩罚权重的平方和,迫使权重W尽可能趋近于0,从而降低模型的拟合能力------让模型无法"过度放大"噪声特征的影响,只能学习数据中普遍存在的、影响较小但更稳定的核心特征。
通俗来说,一组数据会有很多特征,例如本例中的正弦曲线,周期波动是其主要的特征,因此学习该特征对应的权重就大,而噪声也会对应特征,但这些特征就不是我们想学到的,L2 会让所有的权重衰减,大特征(主要特征)衰减后仍然保留(只是值变小),而小特征(噪声特征)会衰减到非常接近 0,其影响被大幅削弱。
当然,也有些小特征确实在数据中存在且需要的,这些权重同样会被衰减、数值变小,可能导致其有效影响被削弱,这就是 L2 正则化的问题。
补充说明:为什么不惩罚偏置b?偏置b是模型的常数项,对模型复杂度的影响远小于权重W;如果惩罚偏置b,可能会导致模型的拟合能力过度下降,反而出现欠拟合。因此,深度学习中,正则化通常只作用于权重W。
4.2 L1正则化:稀疏化权重
L1正则化的正则项R(θ)R(\theta)R(θ),是模型所有权重参数的绝对值之和,公式如下:
R(θ)=∑i∣Wi∣R(\theta) = \sum_{i} |W_i|R(θ)=i∑∣Wi∣
加入L1正则化后,损失函数的偏导数为:
∂Lreg∂W=∂L(θ)∂W+λ⋅sign(W)\frac{\partial L_{reg}}{\partial W} = \frac{\partial L(\theta)}{\partial W} + \lambda \cdot sign(W)∂W∂Lreg=∂W∂L(θ)+λ⋅sign(W)
其中sign(W)sign(W)sign(W)是符号函数:当W>0时,sign(W)=1;当W<0时,sign(W)=-1;当W=0时,sign(W)=0。
L1正则化的特点
L1正则化的核心作用是"稀疏化权重"------由于sign(W)的存在,它会迫使一部分权重W趋近于0,甚至等于0。这相当于"自动筛选特征":权重为0的特征,相当于被模型放弃,模型只保留权重非0的核心特征,从而降低模型复杂度,解决过拟合。
对比L2和L1:L2正则化让权重"普遍变小",但不会让权重变为0;L1正则化让权重"稀疏化",会让部分权重变为0。在深度学习中,L2正则化更常用(因为稀疏化权重可能导致模型欠拟合,且L2的梯度计算更稳定),我们后续的代码演示也将使用L2正则化。
此外,如果大家学习过范数相关的知识,L1和L2正则化的本质就是向量的范数
五、代码演示:用正则化解决过拟合
下面我们基于前文的过拟合场景,在模型中加入L2正则化,看看它如何解决过拟合问题。我们将使用PyTorch中的权重衰减(weight decay)实现L2正则化(PyTorch中,weight decay本质就是L2正则化,直接在优化器中设置即可),沿用相同的数据集和模型结构,只添加正则项,对比过拟合模型和正则化模型的表现。
5.1 正则化模型代码实现
python
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import TensorDataset, DataLoader, random_split
# 1. 复用前文的带噪声正弦曲线数据(和过拟合场景完全一致,转换为PyTorch张量)
np.random.seed(42)
x_np = np.linspace(0, 2*np.pi, 100)
y_true_np = np.sin(x_np)
y_noise_np = y_true_np + 0.1 * np.random.randn(100)
# 转换为PyTorch张量,维度和数据类型与前文一致
x = torch.tensor(x_np, dtype=torch.float32).unsqueeze(1)
y_true = torch.tensor(y_true_np, dtype=torch.float32).unsqueeze(1)
y_noise = torch.tensor(y_noise_np, dtype=torch.float32).unsqueeze(1)
# 2. 复用训练集和验证集划分、DataLoader(与过拟合场景完全一致)
dataset = TensorDataset(x, y_noise)
train_size = int(0.8 * len(dataset))
val_size = len(dataset) - train_size
train_dataset, val_dataset = random_split(dataset, [train_size, val_size])
train_loader = DataLoader(train_dataset, batch_size=16, shuffle=True)
val_loader = DataLoader(val_dataset, batch_size=16, shuffle=False)
# 3. 构建加入L2正则化的模型(和过拟合模型结构一致,通过优化器设置weight decay实现L2正则)
class RegularizedModel(nn.Module):
def __init__(self):
super(RegularizedModel, self).__init__()
# 模型结构与过拟合模型完全一致,不修改网络层
self.fc1 = nn.Linear(1, 64)
self.fc2 = nn.Linear(64, 64)
self.fc3 = nn.Linear(64, 64)
self.fc4 = nn.Linear(64, 1)
self.relu = nn.ReLU()
def forward(self, x):
# 前向传播逻辑与过拟合模型完全一致
x = self.relu(self.fc1(x))
x = self.relu(self.fc2(x))
x = self.relu(self.fc3(x))
x = self.fc4(x)
return x
regularized_model = RegularizedModel() # 实例化正则化模型
# 4. 定义优化器和损失函数(核心:添加weight_decay=0.01,实现L2正则化,对应原lambda=0.01)
criterion = nn.MSELoss() # 损失函数与过拟合模型一致
# weight_decay=0.01 即L2正则化强度λ=0.01,PyTorch会自动将正则项加入损失函数
optimizer = optim.Adam(regularized_model.parameters(), lr=0.001, weight_decay=0.01)
# 5. 训练模型(与过拟合模型训练逻辑一致,500轮、相同批次)
epochs = 500
train_losses_reg = [] # 记录正则化模型训练损失
val_losses_reg = [] # 记录正则化模型验证损失
for epoch in range(epochs):
# 训练阶段
regularized_model.train()
train_loss = 0.0
for inputs, labels in train_loader:
optimizer.zero_grad()
outputs = regularized_model(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
train_loss += loss.item() * inputs.size(0)
train_loss_avg = train_loss / len(train_loader.dataset)
train_losses_reg.append(train_loss_avg)
# 验证阶段
regularized_model.eval()
val_loss = 0.0
with torch.no_grad():
for inputs, labels in val_loader:
outputs = regularized_model(inputs)
loss = criterion(outputs, labels)
val_loss += loss.item() * inputs.size(0)
val_loss_avg = val_loss / len(val_loader.dataset)
val_losses_reg.append(val_loss_avg)
# 6. 预测并可视化结果(与过拟合模型预测逻辑一致)
regularized_model.eval()
with torch.no_grad():
y_pred_reg = regularized_model(x).numpy() # 正则化模型预测
y_pred_overfit_np = y_pred_overfit # 复用前文过拟合模型预测结果
x_np = x.numpy().squeeze()
y_true_np = y_true.numpy().squeeze()
y_noise_np = y_noise.numpy().squeeze()
# 绘制对比图(过拟合 vs 正则化,与原图风格、标签一致)
plt.figure(figsize=(12, 6))
plt.scatter(x_np, y_noise_np, color='orange', label='带噪声的训练数据', alpha=0.6)
plt.plot(x_np, y_true_np, color='blue', label='真实正弦曲线', linewidth=2)
plt.plot(x_np, y_pred_overfit_np.squeeze(), color='red', label='过拟合模型预测', linewidth=2, linestyle='--')
plt.plot(x_np, y_pred_reg.squeeze(), color='green', label='L2正则化模型预测', linewidth=2)
plt.xlabel('x')
plt.ylabel('y = sin(x) + 噪声')
plt.title('过拟合 vs L2正则化:模型预测效果对比')
plt.legend()
plt.show()
# 输出训练集和验证集损失(对比过拟合模型,与原输出格式一致)
train_loss_reg = train_losses_reg[-1]
val_loss_reg = val_losses_reg[-1]
print("="*50)
print("过拟合模型:")
print(f"训练集损失:{train_loss_overfit:.6f},验证集损失:{val_loss_overfit:.6f}")
print("="*50)
print("L2正则化模型:")
print(f"训练集损失:{train_loss_reg:.6f},验证集损失:{val_loss_reg:.6f}")
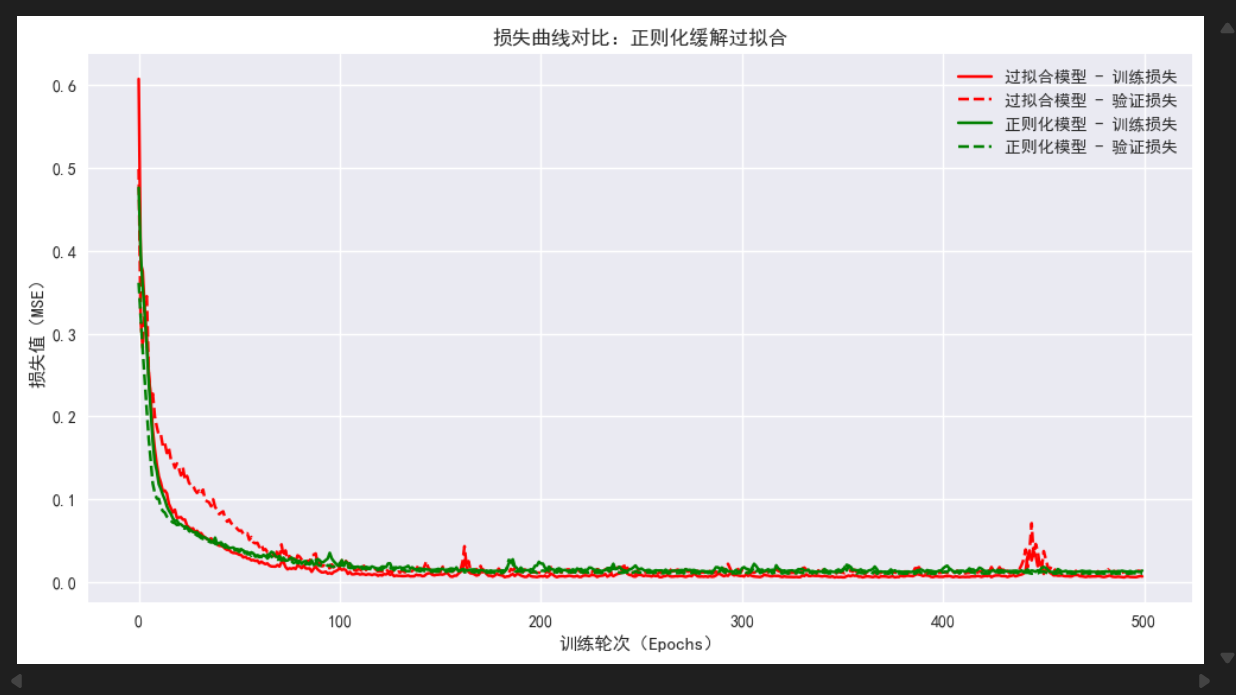
# 绘制损失曲线(观察训练过程中的损失变化,与原图风格、标签一致)
plt.figure(figsize=(12, 6))
plt.plot(train_losses, color='red', label='过拟合模型 - 训练损失')
plt.plot(val_losses, color='red', linestyle='--', label='过拟合模型 - 验证损失')
plt.plot(train_losses_reg, color='green', label='正则化模型 - 训练损失')
plt.plot(val_losses_reg, color='green', linestyle='--', label='正则化模型 - 验证损失')
plt.xlabel('训练轮次(Epochs)')
plt.ylabel('损失值(MSE)')
plt.title('损失曲线对比:正则化缓解过拟合')
plt.legend()
plt.show()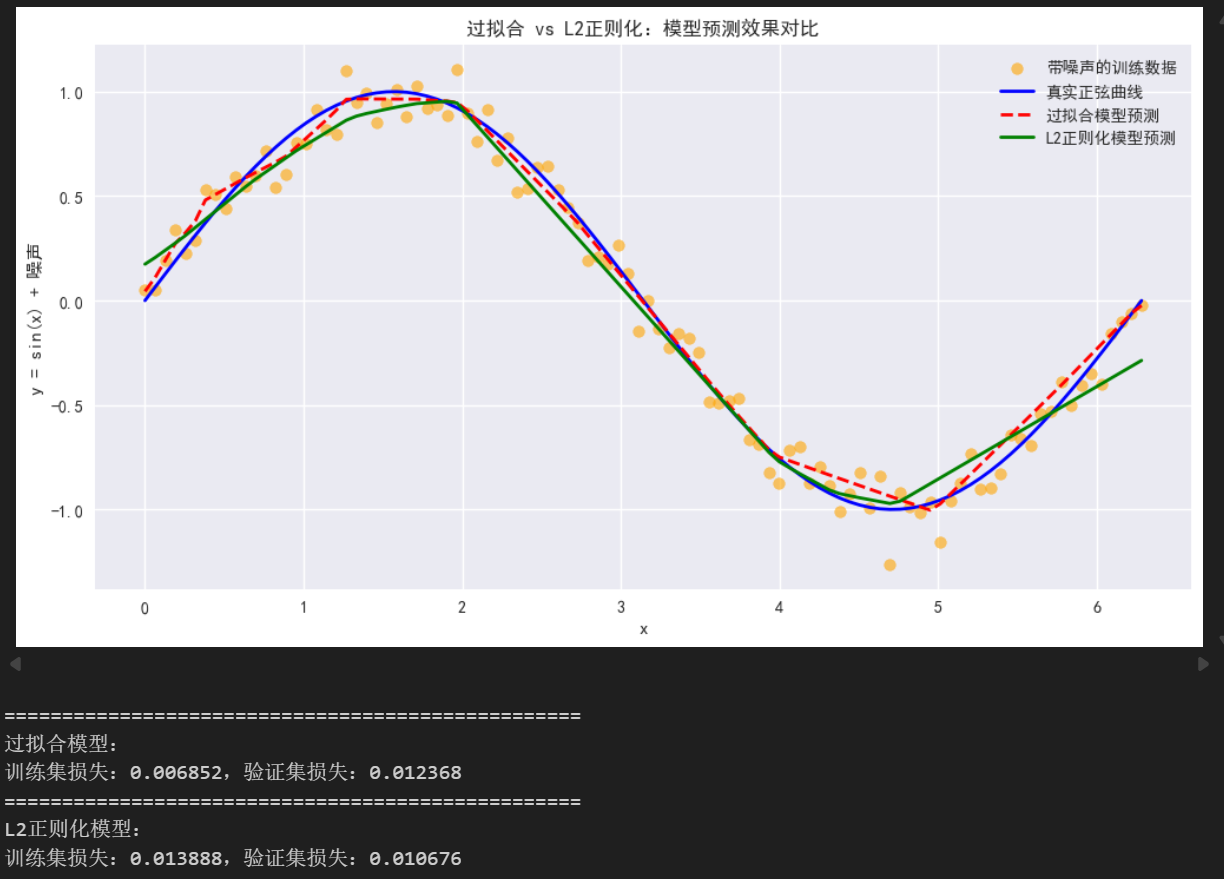
5.2 结果分析:正则化的效果
运行上述代码后,你会观察到三个关键变化,这正是正则化的作用体现:
-
预测曲线更贴合真实趋势:绿色的正则化模型预测曲线,不再像红色过拟合曲线那样崎岖,而是基本贴合蓝色的真实正弦曲线,成功忽略了噪声的干扰;
-
训练损失略有上升,但验证损失大幅下降:过拟合模型的训练损失极低(≈0.006),但验证损失很高(≈0.013);正则化模型的训练损失有上升(≈0.013),但验证损失却下降了(≈0.011)------这说明模型在训练集和验证集上的表现差不多,放弃了"完美拟合噪声",转而学习核心规律,泛化能力显著提升;
-
损失曲线收敛更稳定:过拟合模型的训练损失和验证损失"差距越来越大"(验证损失先降后升),而正则化模型的训练损失和验证损失"差距很小",且都能稳定收敛------这正是正则化约束模型复杂度的效果。
当然,本例仍然比较简单,对正则化的表现可能不太明显,大家可以用其它的例子自行尝试。
5.3 正则化强度λ的选择
正则化强度λ\lambdaλ是一个超参数,需要我们手动调整,不同的λ\lambdaλ会产生不同的效果:
-
λ=0\lambda = 0λ=0:无正则化,模型就是我们前文的过拟合模型;
-
λ\lambdaλ过小(如0.001):惩罚太弱,无法有效缓解过拟合;
-
λ\lambdaλ过大(如0.1):惩罚太强,模型权重被过度压缩,会导致欠拟合(训练损失和验证损失都很高,模型无法拟合真实数据趋势)。
在实际应用中,我们通常通过"网格搜索"或"随机搜索",结合验证集损失,选择最优的λ\lambdaλ值------这也是我们前文提到的"超参数调优"的一部分。
六、总结
到这里,我们已经完整讲解了过拟合与正则化的核心逻辑,结合专栏前文的知识,我们可以总结出几个关键要点,帮你巩固记忆:
-
过拟合的本质:模型复杂度超过数据复杂度,学习到了训练数据中的噪声和偶然特征,泛化能力下降;
-
正则化的核心:通过在损失函数中加入惩罚项,约束模型权重,降低模型复杂度,平衡"拟合能力"和"泛化能力";
-
数学逻辑:L2正则化通过"权重衰减"让权重普遍变小,L1正则化通过"稀疏化权重"筛选核心特征,二者均通过修改损失函数的梯度,改变参数更新方向;
-
实践要点:深度学习中优先使用L2正则化,重点调整正则化强度λ\lambdaλ,避免过拟合和欠拟合。
正则化是深度学习中"防止模型过拟合"的基础方法,后续我们还会学习 dropout、早停(Early Stopping)等更复杂的防过拟合方法,而这些方法的核心思想,都源于我们今天讲解的约束模型复杂度。