背包问题动态规划

_F_y2026-02-18 9:39

01背包

题目描述

01背包



算法原理和实现

身经百战的我们立刻可以根据经验得出状态表示:

dp[i]为选取前i个物品的最大价值,但是问题在于我们不知道[0,i-1]的选取情况就不知道容积.

因此我们必须要增加一个状态:

dp[i][j]表示容积为j时,在前i个物品中选取的最大价值.

那么对于第i个物品,我们有选取和不选取两种情况:

  1. 不选取,dp[i][j]=dp[i-1][j]
  2. 选取dp[i][j]=dp[i-1][j-v[i]]+w[i]

我们取两者最大值即可.

那如果背包一定要装满呢?

很简单,我们将状态表示改为:

dp[i][j]表示容积为j时,在前i个物品中选取的最大价值且物品体积恰好为j.

并且我们可以用-1来标记没有办法装满的情况.

具体实现:

cpp 复制代码 
#include <iostream>
#include <vector>
using namespace std;

int main(){
    int v,n;
    cin>>n>>v;
    vector<pair<int,int>>bag(n);//v w
    vector<vector<int>>dp(n+1,vector<int>(v+1));
    for(int i=0;i<n;++i)cin>>bag[i].first>>bag[i].second;
    for(int i=1;i<=n;++i){
        for(int j=1;j<=v;++j){
            dp[i][j]=dp[i-1][j];
            if(j-bag[i-1].first>=0){
                dp[i][j]=max(dp[i][j],dp[i-1][j-bag[i-1].first]+bag[i-1].second);
            }
        }
    }
    cout<<dp[n][v]<<endl;
    for(int i=1;i<=v;++i)dp[0][i]=-1;
    for(int i=1;i<=n;++i){
        for(int j=1;j<=v;++j){
            dp[i][j]=dp[i-1][j];
            if(j-bag[i-1].first>=0&&dp[i-1][j-bag[i-1].first]>=0){
                dp[i][j]=max(dp[i][j],dp[i-1][j-bag[i-1].first]+bag[i-1].second);
            }
        }
    }
    cout<<max(dp[n][v],0);
    return 0;
}

时间复杂度和空间复杂度都是O(nV)

不难发现我们每次更新状态都只依赖于前一行的值,因此我们可以进行空间优化:

cpp 复制代码 
#include <iostream>
#include <vector>
using namespace std;

int main(){
    int v,n;
    cin>>n>>v;
    vector<pair<int,int>>bag(n);//v w
    vector<int>dp(v+1);
    for(int i=0;i<n;++i)cin>>bag[i].first>>bag[i].second;
    for(int i=1;i<=n;++i){
        for(int j=v;j>=bag[i-1].first;--j){
            dp[j]=max(dp[j],dp[j-bag[i-1].first]+bag[i-1].second);
        }
    }
    cout<<dp[v]<<endl;
    dp[0]=0;
    for(int i=1;i<=v;++i)dp[i]=-1;
    for(int i=1;i<=n;++i){
        for(int j=v;j>=bag[i-1].first;--j){
            if(dp[j-bag[i-1].first]>=0){
                dp[j]=max(dp[j],dp[j-bag[i-1].first]+bag[i-1].second);
            }
        }
    }
    cout<<max(dp[v],0);
    return 0;
}

时间复杂度O(nV),空间复杂度O(V).并且我们的循环有了常数级的优化.

分割等和子集

题目描述

分割等和子集

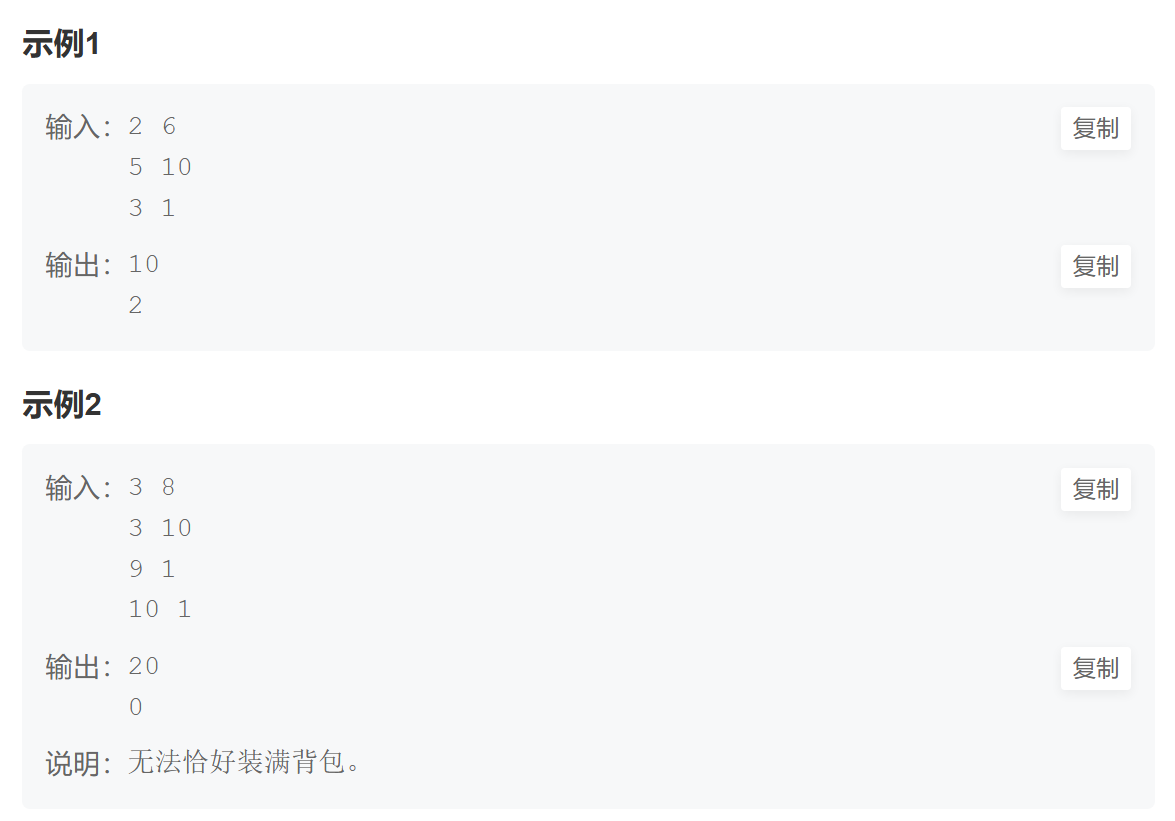
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

示例 1：

输入：nums = [1,5,11,5]

输出：true

解释：数组可以分割成 [1, 5, 5] 和 [11] 。

示例 2：

输入：nums = [1,2,3,5]

输出：false

解释：数组不能分割成两个元素和相等的子集。

提示：

  • 1 <= nums.length <= 200
  • 1 <= nums[i] <= 100

算法原理和实现

将题目转化为能不能从原数组中挑出部分数使得他们的和为数组和的一半.即转化为01背包问题:

cpp 复制代码 
class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int sum=0,n=nums.size();
        for(auto&e:nums)sum+=e;
        if(sum%2)return false;
        sum/=2;
        vector<bool>dp(sum+1);
        dp[0]=true;
        for(int i=1;i<=n;++i){
            for(int j=sum;j>=nums[i-1];--j){
                dp[j]=dp[j]||dp[j-nums[i-1]];
            }
        }
        return dp[sum];
    }
};

时间复杂度O(n sum)空间复杂度O(sum)

目标和

题目描述

目标和

给你一个非负整数数组 nums 和一个整数 target 。

向数组中的每个整数前添加 '+' 或 '-' ，然后串联起所有整数，可以构造一个 表达式 ：

例如，nums = [2, 1] ，可以在 2 之前添加 '+' ，在 1 之前添加 '-' ，然后串联起来得到表达式 "+2-1" 。

返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。

示例 1：

输入：nums = [1,1,1,1,1], target = 3

输出：5

解释：一共有 5 种方法让最终目标和为 3 。

-1 + 1 + 1 + 1 + 1 = 3

+1 - 1 + 1 + 1 + 1 = 3

+1 + 1 - 1 + 1 + 1 = 3

+1 + 1 + 1 - 1 + 1 = 3

+1 + 1 + 1 + 1 - 1 = 3

示例 2：

输入：nums = [1], target = 1

输出：1

提示：

  • 1 <= nums.length <= 20
  • 0 <= nums[i] <= 1000
  • 0 <= sum(nums[i]) <= 1000
  • -1000 <= target <= 1000

算法原理和实现

如果你对数字足够敏感的话,你会发现.我们将原数组分成正数部分a和负数部分b.

那么a-b=target,a+b=sum.

则a=(target+sum)/2

因此这就转化成一个01背包问题:

cpp 复制代码 
class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        int sum=0,n=nums.size();
        for(auto&e:nums)sum+=e;
        if((target+sum)%2||(target+sum)<0)return 0;
        target=(target+sum)/2;
        vector<int>dp(target+1);
        dp[0]=1;
        for(int i=0;i<n;++i){
            for(int j=target;j>=nums[i];--j){
                dp[j]+=dp[j-nums[i]];
            }
        }
        return dp[target];
    }
};

时间复杂度O(nsumtarget)，空间复杂度O(sum*target)

最后一块石头的重量 II

题目描述

最后一块石头的重量 II

有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。

每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

如果 x == y，那么两块石头都会被完全粉碎；

如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。

最后，最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下，就返回 0。

示例 1：

输入：stones = [2,7,4,1,8,1]

输出：1

解释：

组合 2 和 4，得到 2，所以数组转化为 [2,7,1,8,1]，

组合 7 和 8，得到 1，所以数组转化为 [2,1,1,1]，

组合 2 和 1，得到 1，所以数组转化为 [1,1,1]，

组合 1 和 1，得到 0，所以数组转化为 [1]，这就是最优值。

示例 2：

输入：stones = [31,26,33,21,40]

输出：5

提示：

  • 1 <= stones.length <= 30
  • 1 <= stones[i] <= 100

算法原理和实现

正难则反，我们考虑他的反面，如何将问题转化为最大值？

考虑将所有石头质量加起来为sum，那么我们要完全粉碎一块石头x，最终sum会减少2x。

所以我们要使得剩下的质量小，等价于我们从原先石头中选取一堆石头使得他们的两倍质量之和最大且小于等于sum。

最终就转化为了01背包：

cpp 复制代码 
class Solution {
public:
    int lastStoneWeightII(vector<int>& stones) {
        int n=stones.size(),sum=0;
        for(auto&e:stones)sum+=e;
        vector<int>dp(sum+1);
        for(int i=0;i<n;++i){
            for(int j=sum;j>=2*stones[i];--j){
                dp[j]=max(dp[j],dp[j-2*stones[i]]+2*stones[i]);
            }
        }
        return sum-dp[sum];
    }
};

时间复杂度O(n sum),空间复杂度O(sum)

完全背包

题目描述

完全背包


算法原理和实现

我们根据01背包的状态经验：

dp[i][j]表示为在前i个物品中选取使得在j容积下价值最大。

那么第i个物品有选或不选两种情况：

  1. 不选dp[i][j]=dp[i-1][j]
  2. 选。这里就要和01背包区分开来了，因为01背包是只能选取一次，所以选了这个物品后，只能在前i-1个物品进行挑选。但是完全背包是可以无限挑选，因此我们还是可以在前i个物品进行挑选，所以dp[i][j]=dp[i][j-v[i]]+w[i]

最终实现已经空间优化：

cpp 复制代码 
#include <iostream>
#include <vector>
using namespace std;

int main() {
    int n,V;
    cin>>n>>V;
    vector<pair<int,int>>bag(n);
    for(int i=0;i<n;++i)cin>>bag[i].first>>bag[i].second;//v w
    vector<int>dp(V+1);
    for(int i=0;i<n;++i){
        for(int j=bag[i].first;j<=V;++j){
            dp[j]=max(dp[j],dp[j-bag[i].first]+bag[i].second);
        }
    }
    cout<<dp[V]<<endl;
    for(int i=1;i<=V;++i)dp[i]=-1;
    for(int i=0;i<n;++i){
        for(int j=bag[i].first;j<=V;++j){
            if(dp[j-bag[i].first]>=0)
                dp[j]=max(dp[j],dp[j-bag[i].first]+bag[i].second);
        }
    }
    cout<<max(0,dp[V]);
}
// 64 位输出请用 printf("%lld")

时间复杂度O(nV)，空间复杂度O(V)

只需要注意空间优化后，01背包是反向遍历，完全背包是正向遍历。

这是因为01背包依赖的是上一行的元素，而完全背包依赖的是这一行和上一行元素。

零钱兑换

题目描述

零钱兑换

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。

你可以认为每种硬币的数量是无限的。

示例 1：

输入：coins = [1, 2, 5], amount = 11

输出：3

解释：11 = 5 + 5 + 1

示例 2：

输入：coins = [2], amount = 3

输出：-1

示例 3：

输入：coins = [1], amount = 0

输出：0

提示：

  • 1 <= coins.length <= 12
  • 1 <= coins[i] <= 231 - 1
  • 0 <= amount <= 104

算法原理和实现

根据上一题的经验，不难发现，这就是一个完全背包问题

我们定义状态表示为：

dp[i][j]前i种零钱中，能够兑换出j的最少张数。

具体实现：

cpp 复制代码 
class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        vector<int>dp(amount+1);
        int n=coins.size();
        for(int i=1;i<=amount;++i)dp[i]=0x3f3f3f3f;
        for(int i=0;i<n;++i){
            for(int j=coins[i];j<=amount;++j){
                dp[j]=min(dp[j],dp[j-coins[i]]+1);
            }
        }
        return dp[amount]>=0x3f3f3f3f?-1:dp[amount];
    }
};

时间复杂度O(amout n)，空间复杂度O(amout)。

零钱兑换 II

题目描述

零钱兑换 II

给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。

请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。

假设每一种面额的硬币有无限个。

题目数据保证结果符合 32 位带符号整数。

示例 1：

输入：amount = 5, coins = [1, 2, 5]

输出：4

解释：有四种方式可以凑成总金额：

5=5

5=2+2+1

5=2+1+1+1

5=1+1+1+1+1

示例 2：

输入：amount = 3, coins = [2]

输出：0

解释：只用面额 2 的硬币不能凑成总金额 3 。

示例 3：

输入：amount = 10, coins = [10]

输出：1

提示：

  • 1 <= coins.length <= 300
  • 1 <= coins[i] <= 5000
  • coins 中的所有值 互不相同
  • 0 <= amount <= 5000

算法原理和实现

这题和上一题基本一样，就是将状态表示修改一下即可：

cpp 复制代码 
class Solution {
public:
    int change(int amount, vector<int>& coins) {
        int n=coins.size();
        vector<uint>dp(amount+1);
        dp[0]=1;
        for(int i=0;i<n;++i){
            for(int j=coins[i];j<=amount;++j){
                dp[j]+=dp[j-coins[i]];
            }
        }
        return dp[amount];
    }
};

时间复杂度O(amout n)，空间复杂度O(amout).

完全平方数

题目描述

完全平方数

给你一个整数 n ，返回 和为 n 的完全平方数的最少数量 。

完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

示例 1：

输入：n = 12

输出：3

解释：12 = 4 + 4 + 4

示例 2：

输入：n = 13

输出：2

解释：13 = 4 + 9

提示：

  • 1 <= n <= 104

题目描述

题目可以转化为从完全平方数中挑选最少个使得他们之和为n。即完全背包问题：

cpp 复制代码 
class Solution {
public:
    int numSquares(int n) {
        vector<int>nums;
        for(int i=1;i*i<=n;++i)nums.emplace_back(i*i);
        vector<int>dp(n+1);
        int size=nums.size();
        for(int i=0;i<=n;++i)dp[i]=i;//初始化第1行
        for(int i=1;i<size;++i){
            for(int j=nums[i];j<=n;++j){
                dp[j]=min(dp[j],dp[j-nums[i]]+1);
            }
        }
        return dp[n];
    }
};

时间复杂度O(n n \sqrt{n} n )，空间复杂度O(n+1).

一和零

题目描述

一和零

给你一个二进制字符串数组 strs 和两个整数 m 和 n 。

请你找出并返回 strs 的最大子集的长度，该子集中 最多 有 m 个 0 和 n 个 1 。

如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集 。

示例 1：

输入：strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3

输出：4

解释：最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ，因此答案是 4 。

其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3 。

示例 2：

输入：strs = ["10", "0", "1"], m = 1, n = 1

输出：2

解释：最大的子集是 {"0", "1"} ，所以答案是 2 。

提示：

  • 1 <= strs.length <= 600
  • 1 <= strs[i].length <= 100
  • strs[i] 仅由 '0' 和 '1' 组成
  • 1 <= m, n <= 100

算法原理和实现

这就是一个二维费用的背包问题，我们拓展状态表示为：

dp[i][j][k]在前i个元素中挑选且所有元素之和的0长度不超过j，1长度长度不超过k的最多元素个数。

注意i==0的时候意味着没有元素，因此不需要初始化：

cpp 复制代码 
class Solution {
public:
    int cntone(const string&str){
        int cnt=0,n=str.size();
        for(int i=0;i<n;++i)if(str[i]=='1')++cnt;
        return cnt;
    }
    int findMaxForm(vector<string>& strs, int m, int n) {
        int size=strs.size();
        vector<vector<vector<int>>>dp(size+1,vector<vector<int>>(m+1,vector<int>(n+1)));
        for(int i=1;i<=size;++i){
            for(int j=0;j<=m;++j){
                for(int k=0;k<=n;++k){
                    dp[i][j][k]=dp[i-1][j][k];
                    int onelen=cntone(strs[i-1]);
                    int zerolen=strs[i-1].size()-onelen;
                    if(j-zerolen>=0&&k-onelen>=0){
                        dp[i][j][k]=max(dp[i][j][k],dp[i-1][j-zerolen][k-onelen]+1);
                    }
                }
            }
        }
        return dp[size][m][n];
    }
};

时间复杂度和空间复杂度都是O(size*m*n)

我们来进行空间优化：

cpp 复制代码 
class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        int sz=strs.size();
        vector<vector<int>>dp(m+1,vector<int>(n+1));
        for(int i=0;i<sz;++i){
            int onelen=0,zerolen;
            for(const auto e:strs[i]){
                if(e=='1')++onelen;
            }
            zerolen=strs[i].size()-onelen;
            for(int j=m;j>=zerolen;--j){
                for(int k=n;k>=onelen;--k){
                    dp[j][k]=max(dp[j][k],dp[j-zerolen][k-onelen]+1);
                }
            }
        }
        return dp[m][n];
    }
};

空间复杂度O(mn)

盈利计划

题目描述

盈利计划

集团里有 n 名员工，他们可以完成各种各样的工作创造利润。

第 i 种工作会产生 profit[i] 的利润，它要求 group[i] 名成员共同参与。如果成员参与了其中一项工作，就不能参与另一项工作。

工作的任何至少产生 minProfit 利润的子集称为 盈利计划 。并且工作的成员总数最多为 n 。

有多少种计划可以选择？因为答案很大，所以 返回结果模 10^9 + 7 的值。

示例 1：

输入：n = 5, minProfit = 3, group = [2,2], profit = [2,3]

输出：2

解释：至少产生 3 的利润，该集团可以完成工作 0 和工作 1 ，或仅完成工作 1 。

总的来说，有两种计划。

示例 2：

输入：n = 10, minProfit = 5, group = [2,3,5], profit = [6,7,8]

输出：7

解释：至少产生 5 的利润，只要完成其中一种工作就行，所以该集团可以完成任何工作。

有 7 种可能的计划：(0)，(1)，(2)，(0,1)，(0,2)，(1,2)，以及 (0,1,2) 。

提示：

  • 1 <= n <= 100
  • 0 <= minProfit <= 100
  • 1 <= group.length <= 100
  • 1 <= group[i] <= 100
  • profit.length == group.length
  • a0 <= profit[i] <= 100

算法原理和实现

实际上这个题目有些许晦涩，读懂之后其实就是我们的二维费用背包问题。

这里状态表示定义为：

dp[i][j][k]从前i个计划中挑选，总人数不超过j，总利润至少为k，一共有多少种选法。

那么对于第i个计划有选或者不选两种情况，如果不选就是dp[i][j][k]=dp[i-1][j][k].

可如果选的话我们就必须保证j>=group[i]，否则连最基本的人数都不够，无法执行计划。

那么利润是否需要k>=profit[i]，直观来想，如果profit[i]>k，那么我直接选取这个计划是不是就已经利润至少为k了。所以利润是不做限制的。

具体状态转移方程：
d p [ i ] [ j ] [ k ] = d p [ i − 1 ] [ j ] [ k ] dp[i][j][k]=dp[i-1][j][k] dp[i][j][k]=dp[i−1][j][k]
d p [ i ] [ j ] [ k ] + = d p [ i − 1 ] [ j − g r o u p [ i ] ] [ m a x ( 0 , k − p r o f i t [ i ] ) ] w h e r e j ≥ g r o u p [ i ] dp[i][j][k]+=dp[i-1][j-group[i]][max(0,k-profit[i])]\space where \space j≥group[i] dp[i][j][k]+=dp[i−1][j−group[i]][max(0,k−profit[i])] where j≥group[i]

注意初始化，当i=0时，我们只能满足k=0的需求，因此dp[0][j][0]=1

最后我们实现空间优化版本：

cpp 复制代码 
class Solution {
public:
    const int MOD=1e9+7;
    int profitableSchemes(int n, int minProfit, vector<int>& group, vector<int>& profit) {
        vector<vector<int>>dp(n+1,vector<int>(minProfit+1));
        int sz=group.size();
        for(int i=0;i<=n;++i)dp[i][0]=1;
        for(int i=0;i<sz;++i){
            int g=group[i],p=profit[i];
            for(int j=n;j>=g;--j){
                for(int k=minProfit;k>=0;--k){
                    dp[j][k]+=dp[j-g][max(0,k-p)];
                    dp[j][k]%=MOD;
                }
            }
        }
        return dp[n][minProfit];
    }
};

时间复杂度O(sz*n*minProfit),空间复杂度O(n*minProfit).

组合总和 Ⅳ

题目描述

组合总和 Ⅳ

给你一个由 不同 整数组成的数组 nums ，和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素排列的个数。

题目数据保证答案符合 32 位整数范围。

示例 1：

输入：nums = [1,2,3], target = 4

输出：7

解释：

所有可能的组合为：

(1, 1, 1, 1)

(1, 1, 2)

(1, 2, 1)

(1, 3)

(2, 1, 1)

(2, 2)

(3, 1)

请注意，顺序不同的序列被视作不同的组合。

示例 2：

输入：nums = [9], target = 3

输出：0

提示：

  • 1 <= nums.length <= 200
  • 1 <= nums[i] <= 1000
  • nums 中的所有元素 互不相同
  • 1 <= target <= 1000

算法原理和实现

根据示例，我们发现官方是个狡猾的家伙。明明就是排列问题，却要写成组合问题。

所以我们的背包解法是解不了排列问题的。

我们根据经验猜测状态转移方程：

dp[i]为目标为i时，所有元素选取的排列情况。

我们的排列情况无非就分几种情况：

  1. nums[0]结尾
  2. nums[1]结尾
  3. ...
  4. nums.back()结尾

所以我们考虑所有情况，当nums[0]结尾，我们就要知道i-nums[0]的排列情况。

所以填表从左向右即可：

cpp 复制代码 
class Solution {
public:
    int combinationSum4(vector<int>& nums, int target) {
        vector<uint>dp(target+1);
        int n=nums.size();
        dp[0]=1;
        for(int i=1;i<=target;++i){
            for(int j=0;j<n;++j){
                if(i-nums[j]>=0)dp[i]+=dp[i-nums[j]];
            }
        }
        return dp[target];
    }
};

不同的二叉搜索树

题目描述

不同的二叉搜索树

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例 1：

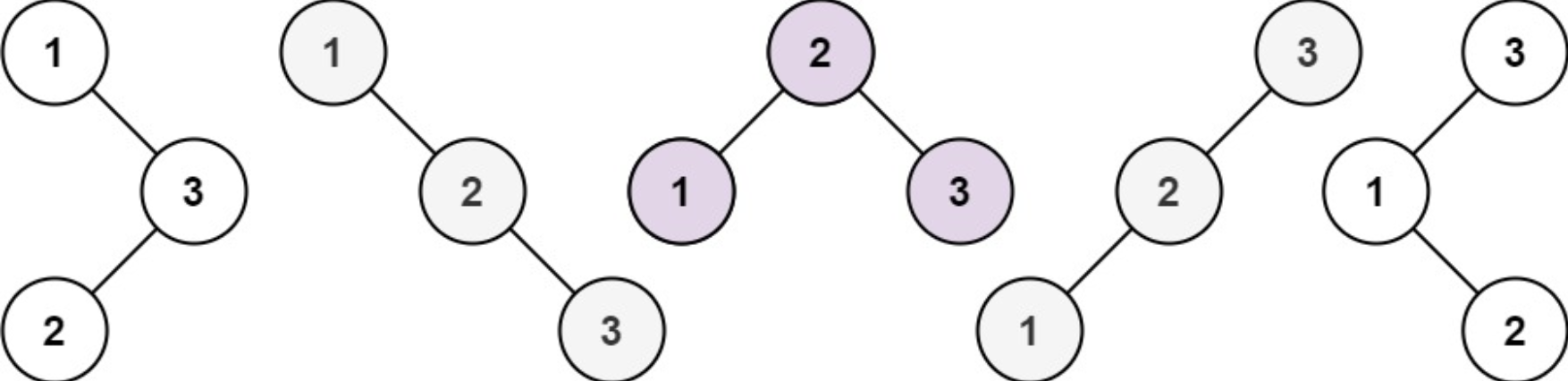
输入：n = 3

输出：5

示例 2：

输入：n = 1

输出：1

提示：

  • 1 <= n <= 19

记忆化搜索

我们从递归开始解决这个问题会比较简单。

对于1~n形成二叉搜索树，我们先以n=5举例：

我们要这些结点形成二叉搜索树，实际上可以让任意一个结点当作根节点：

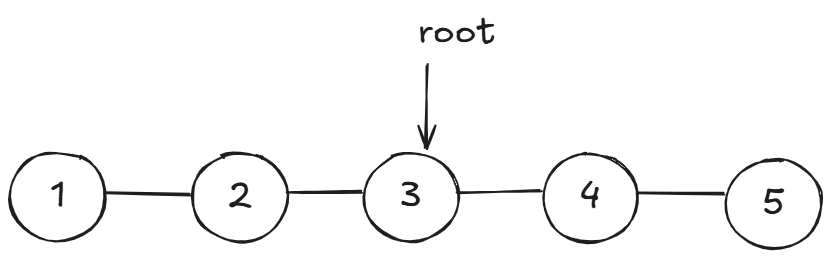
那么我们遍历所有情况即可。

当以3为根节点，我们想要他是一颗二叉搜索树，那么他的左子树和右子树也必须是二叉搜索树。

至此，我们就理清了递归搜索的思路：

cpp 复制代码 
class Solution {
public:
    int numTrees(int n) {
        vector<vector<int>> dp(n+1, vector<int>(n+1));
        function<int(int, int)> dfs = [&](int l, int r) {
            if (l >= r)
                return 1;
            if (!dp[l][r]) {
                int ret = 0;
                for (int root = l; root <= r; ++root) {
                    ret += dfs(l, root - 1) * dfs(root + 1, r);
                }
                dp[l][r] = ret;
            }
            return dp[l][r];
        };
        return dfs(1, n);
    }
};

动态规划

那么我们根据刚才实现的记忆化搜索转化成动态规划。

定义状态表示为：

dp[i]结点数为i时能构成二叉搜索树的数目。

初始化dp[0]=1:

cpp 复制代码 
class Solution {
public:
    int numTrees(int n) {
        vector<int>dp(n+1);
        dp[0]=1;
        for(int i=1;i<=n;++i){
            for(int j=0;j<i;++j){//左子树结点数
                dp[i]+=dp[j]*dp[i-j-1];
            }
        }
        return dp[n];
    }
};

时间复杂度O(n2)，空间复杂度O(n).

相关推荐
Frostnova丶1 小时前
LeetCode 401. 二进制手表
算法·leetcode
Wect1 小时前
LeetCode 104. 二叉树的最大深度：解题思路+代码解析
前端·算法·typescript
Wect2 小时前
LeetCode 100. 相同的树：两种解法（递归+迭代）详解
前端·算法·typescript
不会敲代码12 小时前
面试必考：如何优雅地将列表转换为树形结构？
javascript·算法·面试
流云鹤2 小时前
数学入门(快速幂&乘法逆元&GCD&质数&组合数)
算法
努力学算法的蒟蒻2 小时前
day88（2.17）——leetcode面试经典150
算法·leetcode·面试
Anastasiozzzz2 小时前
LeetCode 287 寻找重复数字
算法·leetcode·职场和发展
im_AMBER2 小时前
Leetcode 123 二叉树的层平均值 | 二叉树的右视图 | 二叉树的层序遍历
数据结构·学习·算法·leetcode·二叉树
We་ct2 小时前
LeetCode 100. 相同的树：两种解法（递归+迭代）详解
前端·算法·leetcode·链表·typescript
热门推荐
01从零搭建一个 PHP 登录注册系统（含完整源码）02使用 1panel面板 部署 php网站03GitHub 镜像站点04PHP Error: 常见错误及其解决方法05AI Agent 平台横评：ZeroClaw vs OpenClaw vs Nanobot06Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services07如何将 TRAE IDE 的插件市场源切换至 VS Code 官方市场08openClaw安装飞书插件｜核心踩坑：spawn EINVAL 错误终极解决指南09MIUI显示/隐藏5G开关的方法，信号弱时开启手机Wifi通话方法10全面体验 Grok API 中转站（2025 · Grok 4 系列最新版）