打破模型桎梏!无模型预测控制技术,抗扰性能再升级
在新能源汽车牵引、工业伺服驱动等关键领域,表面贴式永磁同步电机(SMPMSM)凭借高效能、高功率密度的优势占据核心地位。但实际工况中,电机参数易受温升、磁饱和影响(定子电阻波动可达 40%,永磁磁链变化超 20%),加之逆变器死区、功率开关非理想特性带来的非线性干扰,传统 PI 控制依赖精确数学模型的弊端愈发凸显 ------ 电流畸变、转矩脉动、动态响应滞后等问题直接制约系统性能,甚至可能引发运行失稳。
为突破这一技术瓶颈,无模型控制(MFC)凭借 "不依赖精确数学模型,仅靠输入输出数据实现精准控制" 的核心优势,成为解决参数不确定性与逆变器非线性难题的全新路径。本文详解的 SMPMSM 无模型电流控制方案,通过构建超局部模型实现扰动自适应补偿,经仿真与实验验证,其动态响应与稳态精度均远超传统 PI 控制。
一、核心思维:超局部模型替代传统精确建模
传统 PI 控制的设计基础是 SMPMSM 的 dq 轴数学模型,需精确知晓电机参数,其完整表达式为:
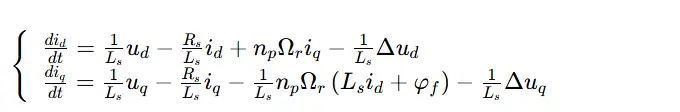
其中,Rs(定子电阻)、Ls(定子电感)、φf(永磁磁链)等参数的动态漂移,以及Δud、Δuq代表的逆变器非线性扰动,都会导致模型失配,进而恶化控制性能。
无模型控制的关键突破在于超局部模型,它彻底脱离对精确参数的依赖,仅通过系统输入输出数据刻画动态特性:
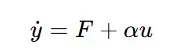
将其适配到 dq 轴电流控制中,得到:
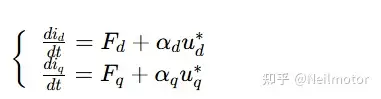
该模型的核心设计逻辑的是:
Fd、Fq:集总扰动项,将参数漂移、逆变器非线性、交叉耦合电压等所有未知干扰 "打包整合",无需解析其物理本质,仅需在线实时估计;
αd、αq:比例因子,用于匹配控制量与输出变化率的量级,调整简单灵活,无需复杂参数优化;
ud∗、uq∗:dq轴电压参考值,替代难以直接测量的逆变器实际输出电压,降低硬件实现难度。
二、具体实现:数据驱动的扰动补偿与精准控制
基于超局部模型,无模型电流控制器的核心是通过在线估计集总扰动F,实现扰动补偿与电流精准跟踪。具体设计流程如下:
2.1. 集总扰动在线估计
采用代数参数辨识技术,在滑动时间窗口[0,T](T=nF*Ts,nF为窗口长度,Ts为采样周期)内,利用输入输出数据实时计算F的估计值F^。以 q 轴为例,离散化实现公式为:
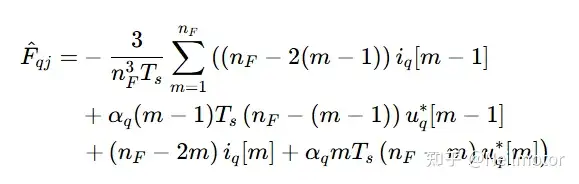
该算法本质是带遗忘特性的滑动窗口积分器,既能快速跟踪扰动动态变化,又能有效抑制测量噪声,为控制精度提供保障。
2.2. 核心控制律推导
结合跟踪误差e=i−i(i∗为电流参考值),引入比例控制项实现误差校正,最终得到 dq 轴电流控制律:
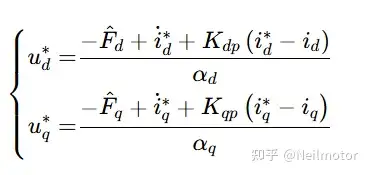
· i˙d∗=0(采用 MTPA 控制策略,d 轴电流参考值设为 0 以实现最大转矩电流比);
· i˙q∗=(iq∗[m]−iq∗[m−1])/Ts(q轴电流参考值的一阶数值微分,保证数字传输的可靠性与低噪声);
· Kdp、Kqp:dq轴比例增益,仅需单参数调整即可优化系统跟踪性能,无需复杂整定。
2.3. 系统实现架构
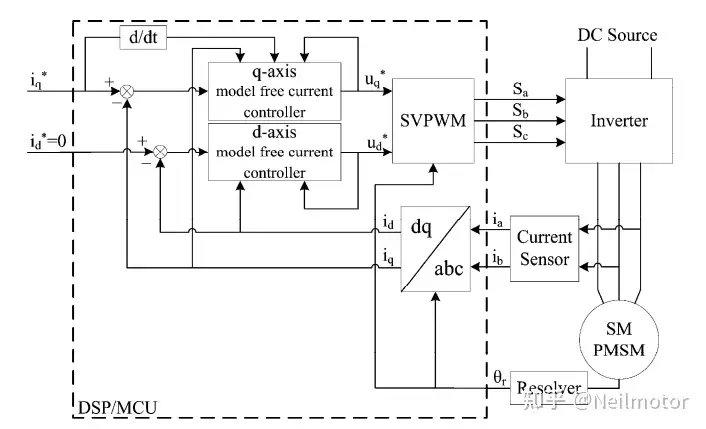
整个控制系统架构简洁高效,核心包含三大模块:
(1)数据采集模块:通过电流传感器获取 dq轴定子电流id、iq,resolver 测量转子位置与转速Ωr;
(2)扰动估计模块:基于滑动窗口内的输入(ud∗、uq∗)输出(id、iq)数据,实时计算F^d、F^q;
(3)控制输出模块:根据控制律计算电压参考值,经 SVPWM 逆变器输出驱动电机,实现电流精准跟踪。
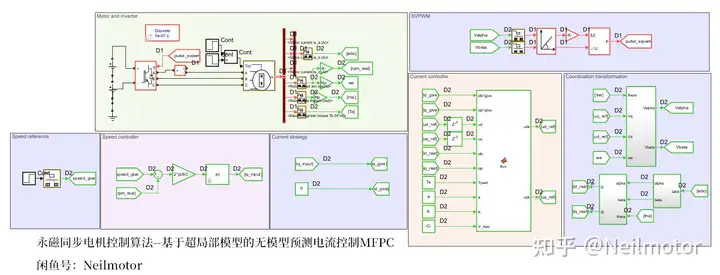
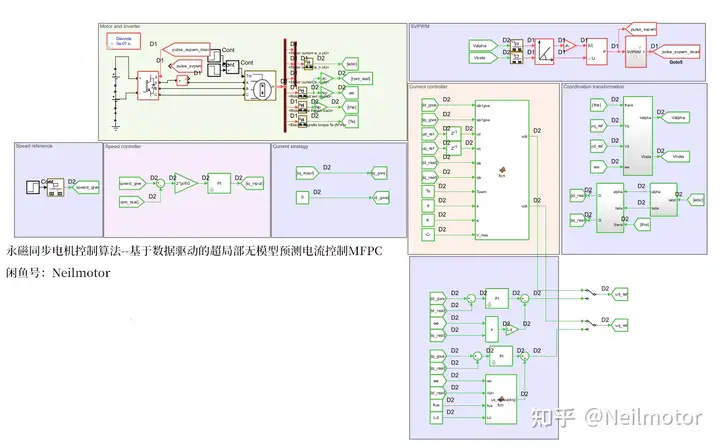
三、仿真模型
在MATLAB/simulink里面验证所提算法,搭建离散化仿真。采用和实验中一致的采样、控制周期1e-4,电机部分计算周期为5e-7。
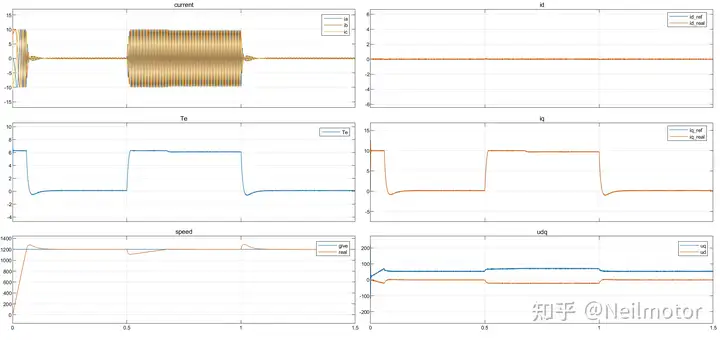
**仿真工况:**给定转速1200rpm,0.5s施加额定负载,1s撤去负载。
这里为什么设置1200rpm,并非1000rpm这种整齐的数值呢?主要是根据公式n=60*f/p,转速为1200rpm时计算出的电频率是个整数,便于进行FFT分析。
额定参数下仿真波形:
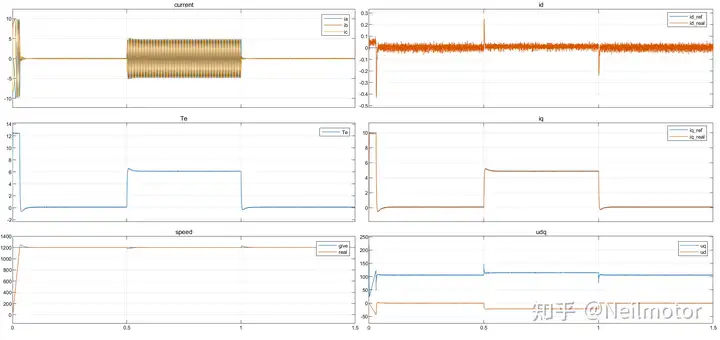
对A相电流进行FFT分析
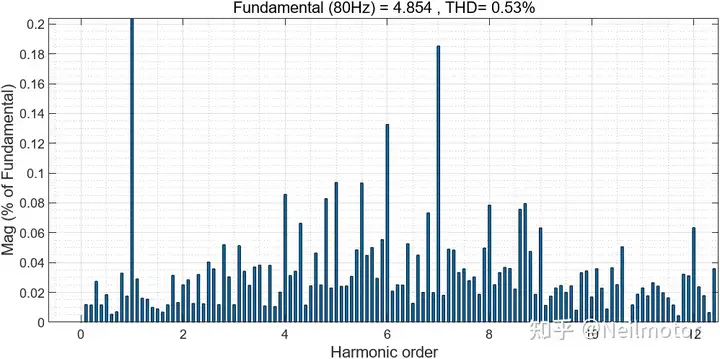
0.5倍额定参数下仿真波形:
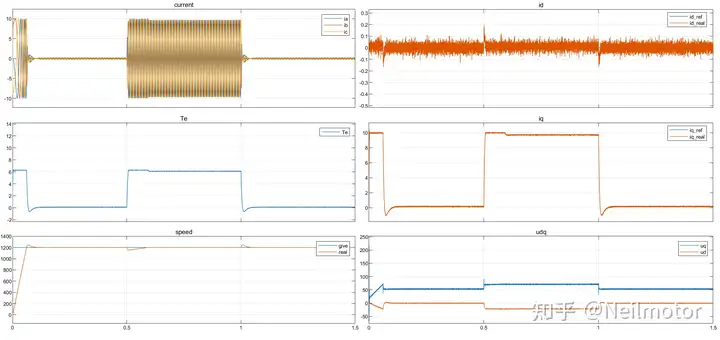
对A相电流进行FFT分析
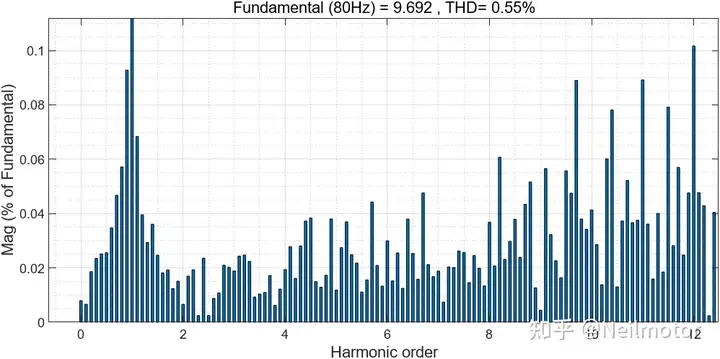
从FFT分析可以看出,由于电机转子磁链缩小为0.5倍,输出相同转矩时,电子电流扩大为2倍。
1.5倍额定参数下仿真波形:
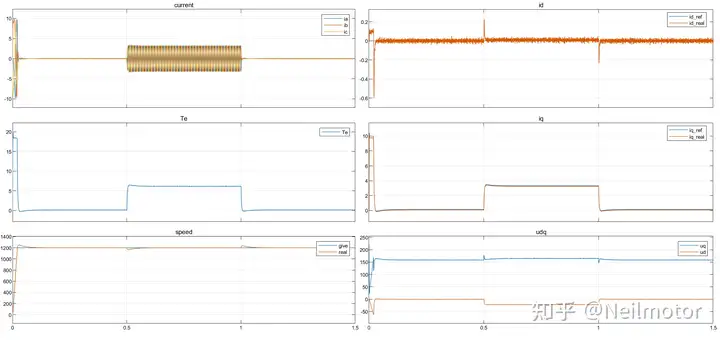
对A相电流进行FFT分析
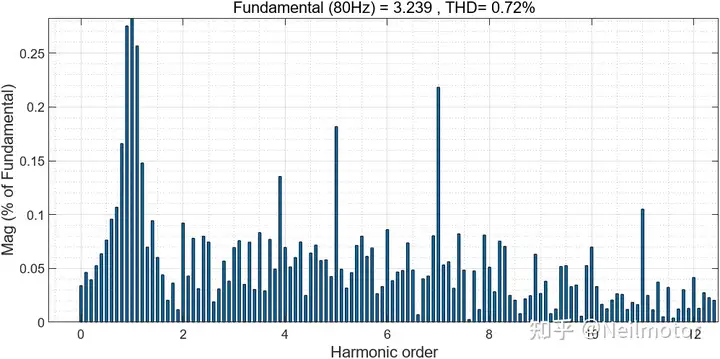
上述仿真测试中,a并未取额定电感值倒数。未测试算法对参数a的鲁棒性,现将a增大至2倍原值,K、nT保持不变,测试在0.5倍额定参数下电机状态
仿真波形:
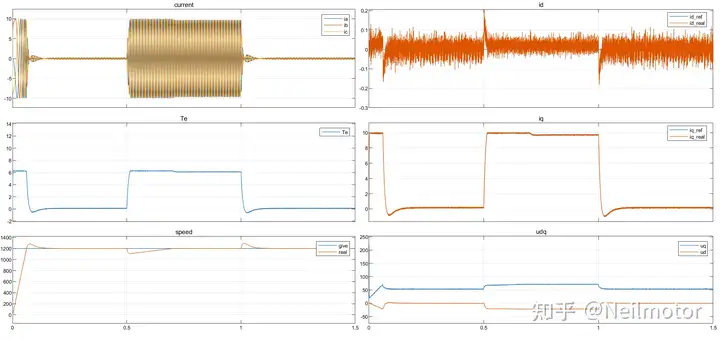
对A相电流进行FFT分析
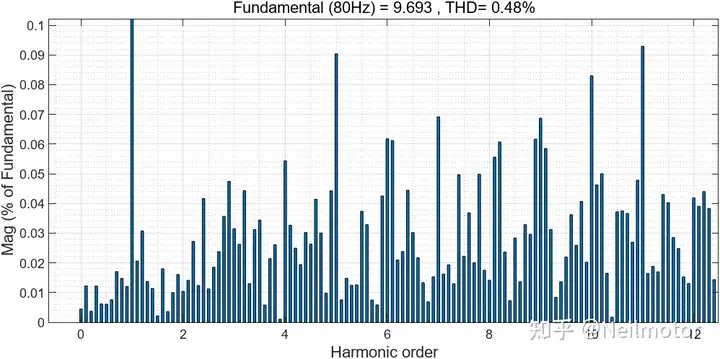
电机控制性能依旧很好,在加载时电机转速恢复较慢,是由于dq轴电流已达到限幅值,有需要的小伙伴可以将该值设置大一些或者按照实物设置。
总结:相比传统依赖精确模型的控制方案,本无模型控制技术具有三大核心优势:
1.**鲁棒性更强:**彻底摆脱电机参数依赖,自动适应参数漂移与逆变器非线性,无需额外扰动观测器;
2.**控制性能更优:**动态响应快,稳态精度高;
3.**工程实现更易:**控制参数少,只有a、K、nT三个参数、整定简单,计算量小,主流 DSP 可轻松实现实时控制,无需复杂硬件升级。
该技术不仅适用于表面贴式永磁同步电机,还可拓展至内置式永磁同步电机(IPMSM),为新能源汽车、工业伺服等对可靠性与鲁棒性要求极高的场景提供了高性能驱动解决方案,有望成为替代传统PI控制的下一代核心技术。
四、抗逆变器非线性扰动能力
上文的参考文献是

文章提出该方法可以应对逆变器非线性的影响,在上篇博客中没有进行验证,在这里进行补充。设置仿真条件:转速环采用传统PI控制,电流环分别采用带宽为400Hz的PI调节器和文章提出的MFC(Model-free Control),转速设定为60rpm(低速且方便计算频率),死区时间为2us。
仿真波形:
PI调节器:
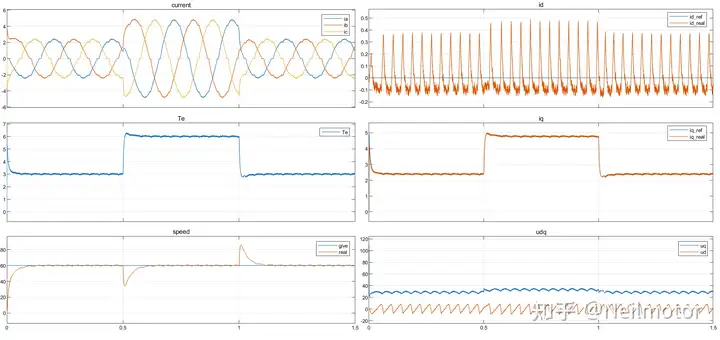
此时三相电流THD为5.84%
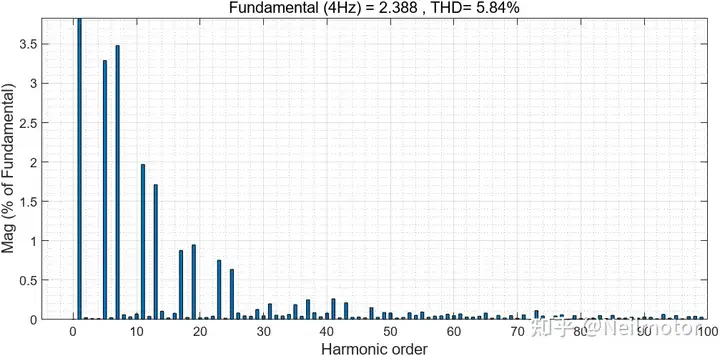
MFC:
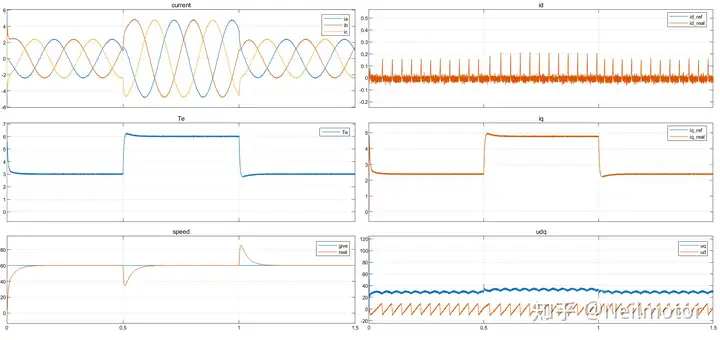
三相电流THD由5.84%降低至1.72%,从上图中也可以看出,三相电流的正弦度明显提升,d轴电流波动-0.15-0.3降低至-0.05-0.2,且d轴保持在给定值0附近
五、无模型无差拍预测电流控制改进
上文所提文章发表于2016年,在18年作者又发布了以下文章

基本思想并未变化,仍然是通过一个滑动窗口估算F,只是对udref,uqerf的计算进行了优化。文献1的电压计算公式为:
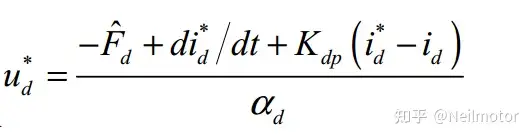
文献2的电压计算公式为:
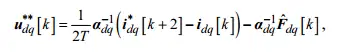
相比之下,消除了参数K,进一步优化了算法的复杂程度和调试难度,因此改进之后算法只剩下参数a和窗口数量n需要进行设置。a的初始值可以设置为电感的倒数,存在一定偏差对算法影响不大。而n可以取值5-20,这里就取10。先对逆变器死区的影响进行讨论。
仿真波形:
改进MFC:
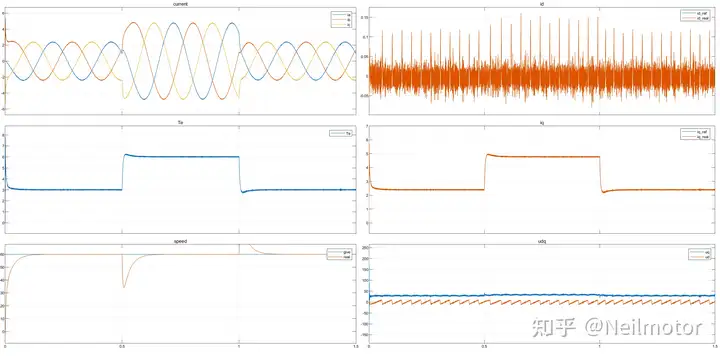
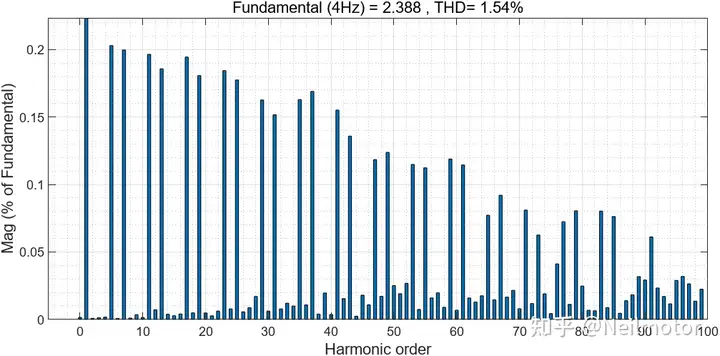
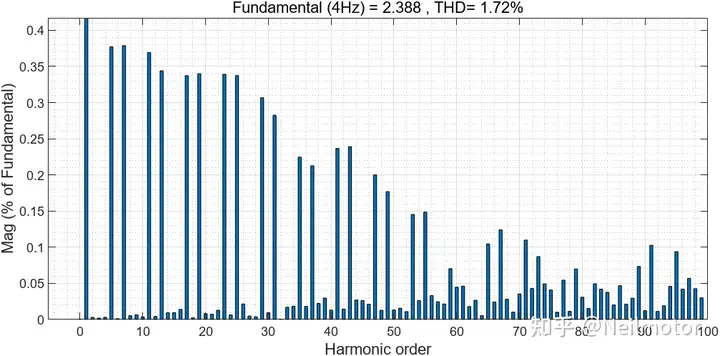
THD相较于改进前降低0.18%
最后在放一下该算法在0.5倍额定参数下仿真波形,: