236. 二叉树的最近公共祖先

中等

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为："对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。"

示例 1：

复制代码

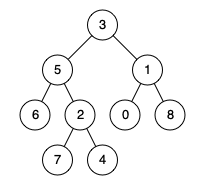
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2：

复制代码

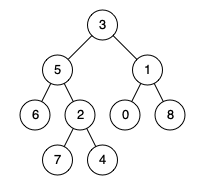
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

复制代码

输入：root = [1,2], p = 1, q = 2
输出：1

提示：

树中节点数目在范围 [2, 105] 内。
-109 <= Node.val <= 109
所有 Node.val 互不相同 。
p != q
p 和 q 均存在于给定的二叉树中。

📝 核心笔记：二叉树的最近公共祖先 (Lowest Common Ancestor - LCA)

1. 核心思想 (一句话总结)

"向上汇报机制：如果左边找到了人，右边也找到了人，那我就是老大；如果只有一边找到了人，那我就把那个人的线索继续往上交。"

后序遍历 (Bottom-Up)：我们需要先知道左右子树的情况，才能判断当前节点是不是 LCA。
两种情况：

1. 分居两侧 ：p 在左子树，q 在右子树 -> 当前节点是 LCA。
2. 父子关系 ：p 是 q 的祖先（或者反之） -> p 直接就是 LCA（因为代码一遇到 p 就返回了，根本不会去遍历 q）。

2. 算法流程 (递归三步曲)

终止条件 (Base Case)：

- root == null：到底了还没找到，返回 null。
- root == p 或 root == q：找到其中一个了！ 直接返回当前节点。

- - 关键点：这里不需要继续递归子树了。如果另一个节点在下面，那当前节点就是 LCA；如果另一个在别处，当前节点也是"候选人"之一。

递归 (Recurse)：

- 去左边找：left = lowestCommonAncestor(root.left, p, q)
- 去右边找：right = lowestCommonAncestor(root.right, p, q)

判断与汇报 (Merge)：

- 左右都有 ( left != null && right != null**)** ：说明 p 和 q 分别在我的两侧。我是 LCA ，返回 root。
- 只有一边有 ：说明 p 和 q 都在那一侧（或者只找到了其中一个），返回找到的那一边 (left 或 right)。
- 都没有 ：返回 null。

🔍 代码回忆清单

复制代码

// 题目：LC 236. Lowest Common Ancestor of a Binary Tree
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        // 1. Base Case: 遇到 null 或者 遇到目标节点，直接返回
        // 这一步隐式地处理了"p 是 q 的祖先"这种情况
        if (root == null || root == p || root == q) {
            return root; 
        }

        // 2. 后序遍历：去左右子树寻找线索
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);

        // 3. 核心判断逻辑
        
        // 情况 A: 左右都有返回值 -> 当前 root 就是交汇点
        if (left != null && right != null) { 
            return root; 
        }
        
        // 情况 B & C: 只有一边有返回值，或者都没返回值
        // 如果左边有，返左边；如果右边有，返右边；都无返 null
        return left != null ? left : right;
    }
}

⚡ 快速复习 CheckList (易错点)

为什么遇到 p****就直接返回，不找 q****了？

- 这是代码最巧妙的地方。
- 假设 q 在 p 的下面。由于我们一遇到 p 就返回了，我们永远不会访问到 q。
- 但这没关系！递归回到上层时，另一边的子树肯定返回 null。
- 最终代码会执行 return left != null ? left : right，一路把 p 往上送，最后 p 就会成为结果。这符合逻辑：如果 q 是 p 的后代，LCA 就是 p。

二叉搜索树 (BST) 的 LCA (LC 235) 有什么不同？

- BST 有序。不需要遍历整棵树。
- 如果 p < root 且 q < root，去左边。
- 如果 p > root 且 q > root，去右边。
- 否则（一左一右，或者有一个是 root），root 就是 LCA。空间复杂度可以优化到 $O(1)$ 。

🖼️ 数字演练

树：

复制代码

       3
     /   \
    5     1
   / \   / \
  6   2 0   8
     / \
    7   4

Target: p=5, q=4

Visit 3: Call Left(5), Right(1).
Visit 5 : root == p. Return 5. (不再访问 6, 2, 7, 4)
Back to 3 : left = 5. Call Right(1).
Visit 1: Call Left(0), Right(8).

- Visit 0: Return null.
- Visit 8: Return null.
- 1 receives (null, null) -> Return null.

Back to 3 : left = 5, right = null.
Result : Return left (5). -> 正确，5 是 5 和 4 的 LCA。