【算法提高篇】（四）线段树之多个区间操作：懒标记优先级博弈与实战突破

_OP_CHEN2026-02-19 9:21

目录

前言

一、多个区间操作的核心痛点：优先级决定结果

[二、经典组合 1：区间乘 + 区间加（洛谷 P3373【模板】线段树 2）](#二、经典组合 1：区间乘 + 区间加（洛谷 P3373【模板】线段树 2）)

[2.1 核心推导：先乘后加的公式简化](#2.1 核心推导：先乘后加的公式简化)

推导过程：

关键结论：

[2.2 结构体与核心函数设计](#2.2 结构体与核心函数设计)

[2.2.1 结构体定义](#2.2.1 结构体定义)

[2.2.2 核心辅助函数](#2.2.2 核心辅助函数)

（1）pushup：整合左右孩子信息

（2）lazy：更新当前节点的标记与区间和

（3）pushdown：下放标记给左右孩子

[2.2.3 建树、修改、查询操作](#2.2.3 建树、修改、查询操作)

（1）build：建树

[（2）modify：区间修改（支持乘 / 加）](#（2）modify：区间修改（支持乘 / 加）)

（3）query：区间查询和

[2.3 完整实战代码（洛谷 P3373 AC 代码）](#2.3 完整实战代码（洛谷 P3373 AC 代码）)

[2.4 代码测试与验证](#2.4 代码测试与验证)

题目输入示例：

手动计算过程：

[三、经典组合 2：区间重置 + 区间加（洛谷 P1253 扶苏的问题）](#三、经典组合 2：区间重置 + 区间加（洛谷 P1253 扶苏的问题）)

[3.1 核心逻辑：重置标记的 "覆盖性"](#3.1 核心逻辑：重置标记的 “覆盖性”)

[3.2 结构体与核心函数设计](#3.2 结构体与核心函数设计)

[3.2.1 结构体定义](#3.2.1 结构体定义)

[3.2.2 核心辅助函数](#3.2.2 核心辅助函数)

（1）pushup：整合左右孩子最大值

（2）lazy：更新当前节点的标记与最大值

（3）pushdown：下放标记给左右孩子

[3.2.3 建树、修改、查询操作](#3.2.3 建树、修改、查询操作)

（1）build：建树

[（2）modify：区间修改（支持重置 / 加）](#（2）modify：区间修改（支持重置 / 加）)

（3）query：区间查询最大值

[3.3 完整实战代码（洛谷 P1253 AC 代码）](#3.3 完整实战代码（洛谷 P1253 AC 代码）)

[3.4 代码测试与验证](#3.4 代码测试与验证)

题目输入示例：

手动计算过程：

四、多区间操作的通用解题框架

[4.1 步骤 1：确定操作优先级](#4.1 步骤 1：确定操作优先级)

[4.2 步骤 2：设计结构体与懒标记](#4.2 步骤 2：设计结构体与懒标记)

[4.3 步骤 3：实现核心辅助函数](#4.3 步骤 3：实现核心辅助函数)

[4.4 步骤 4：实现建树、修改、查询](#4.4 步骤 4：实现建树、修改、查询)

五、高频易错点总结

[5.1 优先级顺序错误](#5.1 优先级顺序错误)

[5.2 懒标记未清空](#5.2 懒标记未清空)

[5.3 重置标记未清空加法标记](#5.3 重置标记未清空加法标记)

[5.4 数据类型溢出](#5.4 数据类型溢出)

[5.5 线段树空间开太小](#5.5 线段树空间开太小)

总结

前言

在掌握了基础线段树、区间修改（单懒标记）后，算法竞赛中常会遇到更复杂的场景 ------多个区间修改操作共存 ，比如 "区间加 + 区间乘""区间重置 + 区间加"。此时单懒标记已无法满足需求，核心难点在于确定操作的执行优先级：不同修改操作的顺序会直接影响最终结果，若处理不当，不仅会导致答案错误，还可能引发精度问题。

本文将深入拆解多个区间操作的核心逻辑，聚焦懒标记的优先级设计，通过洛谷经典模板题（区间加 + 区间乘、区间重置 + 区间加），手把手实现带多懒标记的线段树，让你彻底攻克这一进阶难点！下面就让我们正式开始吧！

一、多个区间操作的核心痛点：优先级决定结果

先看一个直观的例子：假设对数字 x 先执行 "加 3" 再执行 "乘 2"，结果是 (x+3)*2 = 2x+6；若先执行 "乘 2" 再执行 "加 3"，结果是 2x+3。两种顺序的结果天差地别，这就是多个区间操作的核心痛点 ------操作顺序直接影响最终结果。

线段树的多个区间操作，本质是懒标记的叠加与下放。当一个节点同时存在多个懒标记时，必须明确 "先执行哪个操作、后执行哪个操作"，即确定懒标记的优先级。优先级的设计需满足两个原则：

  1. 结果正确性：确保标记下放后，子节点的信息与实际操作顺序一致；
  2. 计算简便性：避免复杂的公式推导，减少代码出错概率。

常见的多个区间操作组合及优先级结论：

操作组合 优先级结论 核心原因
区间乘（mul）+ 区间加（add） 先乘后加 先乘后加的公式可简化（无精度损失），先加后乘会出现除法，导致精度问题
区间重置（set）+ 区间加（add） 先重置后加 重置操作会覆盖之前的所有状态，加操作仅作用于重置后的数值

接下来，我们通过两个经典例题，详细讲解不同组合的实现逻辑。

二、经典组合 1：区间乘 + 区间加（洛谷 P3373【模板】线段树 2）

题目链接：https://www.luogu.com.cn/problem/P3373

这是最常见的多区间操作组合，要求支持 "区间乘 k""区间加 k""区间求和（取模）" 三种操作。我们先推导优先级公式，再实现完整代码。

2.1 核心推导：先乘后加的公式简化

假设节点当前的懒标记为 mul0（乘法标记）和 add0（加法标记），表示该节点的所有元素需执行 x = x * mul0 + add0。现在新增一组操作："乘 m" 和 "加 a"，需要推导新的懒标记 mul1 和 add1。

推导过程：

原操作：x → x * mul0 + add0

新增操作：先乘 m → (x * mul0 + add0) * m，再加 a → (x * mul0 + add0) * m + a

展开后：x * (mul0 * m) + (add0 * m + a)

因此，新的懒标记满足：

  • 新乘法标记**mul1 = mul0 * m（取模）**；
  • 新加法标记 add1 = add0 * m + a（取模）。

关键结论：

  • 乘法标记的初始值为 1（因为 x * 1 = x，不影响原始值）；
  • 加法标记的初始值为 0（因为 x + 0 = x，不影响原始值）；
  • 标记下放时，必须先传递乘法标记，再传递加法标记，确保子节点的操作顺序正确。

2.2 结构体与核心函数设计

2.2.1 结构体定义

需要维护的信息：

  • 区间左右边界 l/r；
  • 区间和 sum（需取模）；
  • 乘法懒标记 mul（初始 1）；
  • 加法懒标记 add（初始 0）。

C++ 代码：

cpp 复制代码 
typedef long long LL;
const int N = 1e5 + 10;
int mod; // 模数，由输入指定

struct node {
    int l, r;
    LL sum, mul, add; // sum:区间和，mul:乘法标记，add:加法标记
} tr[N << 2]; // 线段树空间开4倍

2.2.2 核心辅助函数

多区间操作的核心是**lazy 函数**（更新当前节点标记）和 pushdown 函数（下放标记），需严格遵循 "先乘后加" 的优先级。

（1）pushup：整合左右孩子信息

基础函数，区间和 = 左孩子和 + 右孩子和（取模）：

cpp 复制代码 
void pushup(int p) {
    tr[p].sum = (tr[p << 1].sum + tr[p << 1 | 1].sum) % mod;
}
（2）lazy：更新当前节点的标记与区间和

接收新增的乘法因子 m 和加法因子 a，根据 "先乘后加" 更新节点信息：

cpp 复制代码 
void lazy(int p, LL m, LL a) {
    auto& t = tr[p];
    // 1. 更新区间和：sum = (sum * m + a * 区间长度) % mod
    t.sum = (t.sum * m + a * (t.r - t.l + 1)) % mod;
    // 2. 更新乘法标记：mul = (mul * m) % mod
    t.mul = t.mul * m % mod;
    // 3. 更新加法标记：add = (add * m + a) % mod
    t.add = (t.add * m + a) % mod;
}
（3）pushdown：下放标记给左右孩子

必须先下放乘法标记，再下放加法标记，确保子节点的操作顺序正确：

cpp 复制代码 
void pushdown(int p) {
    auto& t = tr[p];
    // 只有非初始标记时才需要下放（mul≠1 或 add≠0）
    if (t.mul != 1 || t.add != 0) {
        // 下放标记给左孩子：传递当前节点的 mul 和 add
        lazy(p << 1, t.mul, t.add);
        // 下放标记给右孩子：传递当前节点的 mul 和 add
        lazy(p << 1 | 1, t.mul, t.add);
        // 清空当前节点标记（恢复初始状态）
        t.mul = 1;
        t.add = 0;
    }
}

2.2.3 建树、修改、查询操作

（1）build：建树

初始化节点的区间、和、标记（mul=1，add=0）：

cpp 复制代码 
void build(int p, int l, int r, LL a[]) {
    tr[p] = {l, r, a[l] % mod, 1, 0}; // 初始mul=1，add=0
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(p << 1, l, mid, a);
    build(p << 1 | 1, mid + 1, r, a);
    pushup(p);
}
（2）modify：区间修改（支持乘 / 加）

根据操作类型，调用 lazy 函数更新标记，核心逻辑与单标记一致：

cpp 复制代码 
// 区间修改：[x,y] 执行 乘m + 加a（m=1时仅加，a=0时仅乘）
void modify(int p, int x, int y, LL m, LL a) {
    auto& t = tr[p];
    if (x <= t.l && t.r <= y) {
        lazy(p, m, a); // 完全覆盖，直接更新标记
        return;
    }
    pushdown(p); // 未完全覆盖，先下放标记
    int mid = (t.l + t.r) >> 1;
    if (x <= mid) modify(p << 1, x, y, m, a);
    if (y > mid) modify(p << 1 | 1, x, y, m, a);
    pushup(p); // 整合左右孩子信息
}
（3）query：区间查询和

查询逻辑与单标记一致，需在递归前下放标记：

cpp 复制代码 
LL query(int p, int x, int y) {
    auto& t = tr[p];
    if (x <= t.l && t.r <= y) {
        return t.sum % mod;
    }
    pushdown(p); // 下放标记，确保子节点信息最新
    int mid = (t.l + t.r) >> 1;
    LL res = 0;
    if (x <= mid) res = (res + query(p << 1, x, y)) % mod;
    if (y > mid) res = (res + query(p << 1 | 1, x, y)) % mod;
    return res;
}

2.3 完整实战代码（洛谷 P3373 AC 代码）

结合题目要求，处理输入输出，支持三种操作：

  1. 1 x y k：区间 [x,y] 乘 k；
  2. 2 x y k：区间 [x,y] 加 k；
  3. 3 x y：查询区间 [x,y] 和对 mod 取模。

完整代码：

cpp 复制代码 
#include <iostream>
using namespace std;

typedef long long LL;
const int N = 1e5 + 10;
int mod;

struct node {
    int l, r;
    LL sum, mul, add;
} tr[N << 2];

void pushup(int p) {
    tr[p].sum = (tr[p << 1].sum + tr[p << 1 | 1].sum) % mod;
}

void lazy(int p, LL m, LL a) {
    auto& t = tr[p];
    t.sum = (t.sum * m + a * (t.r - t.l + 1)) % mod;
    t.mul = t.mul * m % mod;
    t.add = (t.add * m + a) % mod;
}

void pushdown(int p) {
    auto& t = tr[p];
    if (t.mul != 1 || t.add != 0) {
        lazy(p << 1, t.mul, t.add);
        lazy(p << 1 | 1, t.mul, t.add);
        t.mul = 1;
        t.add = 0;
    }
}

void build(int p, int l, int r, LL a[]) {
    tr[p] = {l, r, a[l] % mod, 1, 0};
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(p << 1, l, mid, a);
    build(p << 1 | 1, mid + 1, r, a);
    pushup(p);
}

void modify(int p, int x, int y, LL m, LL a) {
    auto& t = tr[p];
    if (x <= t.l && t.r <= y) {
        lazy(p, m, a);
        return;
    }
    pushdown(p);
    int mid = (t.l + t.r) >> 1;
    if (x <= mid) modify(p << 1, x, y, m, a);
    if (y > mid) modify(p << 1 | 1, x, y, m, a);
    pushup(p);
}

LL query(int p, int x, int y) {
    auto& t = tr[p];
    if (x <= t.l && t.r <= y) {
        return t.sum % mod;
    }
    pushdown(p);
    int mid = (t.l + t.r) >> 1;
    LL res = 0;
    if (x <= mid) res = (res + query(p << 1, x, y)) % mod;
    if (y > mid) res = (res + query(p << 1 | 1, x, y)) % mod;
    return res;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    int n, q;
    cin >> n >> q >> mod;
    LL a[N];
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        a[i] %= mod; // 初始值取模
    }
    build(1, 1, n, a);

    while (q--) {
        int op, x, y;
        cin >> op >> x >> y;
        if (op == 1) {
            // 操作1：区间[x,y]乘k
            LL k;
            cin >> k;
            modify(1, x, y, k, 0); // a=0，仅乘
        } else if (op == 2) {
            // 操作2：区间[x,y]加k
            LL k;
            cin >> k;
            modify(1, x, y, 1, k); // m=1，仅加
        } else {
            // 操作3：查询区间[x,y]和
            cout << query(1, x, y) << endl;
        }
    }

    return 0;
}

2.4 代码测试与验证

题目输入示例：

复制代码 
5 5 38
1 5 4 2 3
2 1 4 1  // 区间[1,4]加1
3 2 5    // 查询[2,5]和
1 2 4 2  // 区间[2,4]乘2
2 3 5 5  // 区间[3,5]加5
3 1 4    // 查询[1,4]和

手动计算过程：

  1. 初始数组：[1,5,4,2,3]（mod=38）；
  2. 操作 2（加 1）后：[2,6,5,3,3]，[2,5] 和 = 6+5+3+3=17；
  3. 操作 1（乘 2）后：[2,12,10,6,3]；
  4. 操作 2（加 5）后：[2,12,15,11,8]，[1,4] 和 = 2+12+15+11=40 mod38=2；
  5. 输出结果：17、2，与题目示例一致。

三、经典组合 2：区间重置 + 区间加（洛谷 P1253 扶苏的问题）

题目链接：https://www.luogu.com.cn/problem/P1253

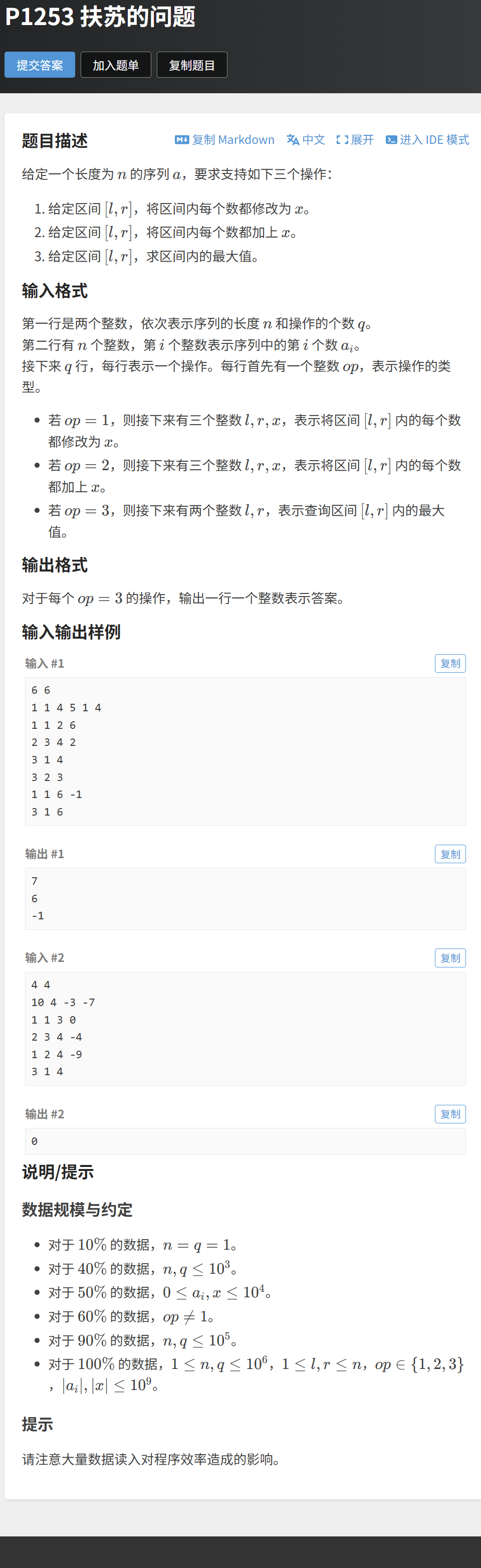
另一类高频组合是**"区间重置（将区间所有元素改为 x）+ 区间加（将区间所有元素加 x）"** 。核心优先级是先重置后加------ 重置操作会覆盖之前的所有状态，加操作仅作用于重置后的数值。

3.1 核心逻辑：重置标记的 "覆盖性"

假设节点存在**"重置标记"** 和 "加法标记"：

  • 若先执行重置（改为 x），再执行加 a，则最终值为 x + a；
  • 若先执行加 a，再执行重置（改为 x），则最终值为 x（加法标记失效）。

因此，重置标记的优先级高于加法标记，标记下放时需先传递重置标记，再传递加法标记。同时，重置标记会清空之前的加法标记（因为重置后加法操作需重新计算）。

3.2 结构体与核心函数设计

3.2.1 结构体定义

需要维护的信息：

  • 区间左右边界 l/r；
  • 区间最大值 max（题目要求查询最大值）；
  • 加法懒标记 add（初始 0）；
  • 重置懒标记 update（初始 0）；
  • 标记状态 st（是否有重置标记，初始 false）。

C++ 代码：

cpp 复制代码 
typedef long long LL;
const int N = 1e6 + 10; // 数据量较大，开1e6+10

struct node {
    int l, r;
    LL max, add, update;
    bool st; // st=true表示有重置标记
} tr[N << 2];

3.2.2 核心辅助函数

（1）pushup：整合左右孩子最大值
cpp 复制代码 
void pushup(int p) {
    tr[p].max = max(tr[p << 1].max, tr[p << 1 | 1].max);
}
（2）lazy：更新当前节点的标记与最大值

根据操作类型（重置 / 加）更新节点信息，遵循 "先重置后加"：

cpp 复制代码 
// st：是否重置，update：重置值，add：增加值
void lazy(int p, bool st, LL update_val, LL add_val) {
    auto& t = tr[p];
    // 1. 先处理重置（优先级更高）
    if (st) {
        t.max = update_val; // 重置为指定值
        t.add = 0; // 重置后清空加法标记
        t.update = update_val;
        t.st = true;
    }
    // 2. 再处理加法
    t.max += add_val;
    t.add += add_val;
}
（3）pushdown：下放标记给左右孩子

先下放重置标记，再下放加法标记，确保子节点操作顺序正确：

cpp 复制代码 
void pushdown(int p) {
    auto& t = tr[p];
    // 有重置标记或加法标记时下放
    if (t.st || t.add != 0) {
        // 下放给左孩子
        lazy(p << 1, t.st, t.update, t.add);
        // 下放给右孩子
        lazy(p << 1 | 1, t.st, t.update, t.add);
        // 清空当前节点标记
        t.st = false;
        t.update = 0;
        t.add = 0;
    }
}

3.2.3 建树、修改、查询操作

（1）build：建树
cpp 复制代码 
void build(int p, int l, int r, LL a[]) {
    tr[p] = {l, r, a[l], 0, 0, false};
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(p << 1, l, mid, a);
    build(p << 1 | 1, mid + 1, r, a);
    pushup(p);
}
（2）modify：区间修改（支持重置 / 加）
cpp 复制代码 
// st：true=重置，false=加法；val：重置值/增加值
void modify(int p, int x, int y, bool st, LL val) {
    auto& t = tr[p];
    if (x <= t.l && t.r <= y) {
        if (st) {
            // 重置操作：add_val=0
            lazy(p, true, val, 0);
        } else {
            // 加法操作：st=false，update_val=0
            lazy(p, false, 0, val);
        }
        return;
    }
    pushdown(p);
    int mid = (t.l + t.r) >> 1;
    if (x <= mid) modify(p << 1, x, y, st, val);
    if (y > mid) modify(p << 1 | 1, x, y, st, val);
    pushup(p);
}
（3）query：区间查询最大值
cpp 复制代码 
LL query(int p, int x, int y) {
    auto& t = tr[p];
    if (x <= t.l && t.r <= y) {
        return t.max;
    }
    pushdown(p);
    int mid = (t.l + t.r) >> 1;
    LL res = -1e18; // 初始值设为极小值
    if (x <= mid) res = max(res, query(p << 1, x, y));
    if (y > mid) res = max(res, query(p << 1 | 1, x, y));
    return res;
}

3.3 完整实战代码（洛谷 P1253 AC 代码）

题目要求支持三种操作：

  1. 1 l r x：区间 [l,r] 重置为 x；
  2. 2 l r x：区间 [l,r] 加 x；
  3. 3 l r：查询区间 [l,r] 最大值。

完整代码：

cpp 复制代码 
#include <iostream>
#include <cstdio>
using namespace std;

typedef long long LL;
const int N = 1e6 + 10;

struct node {
    int l, r;
    LL max, add, update;
    bool st;
} tr[N << 2];

void pushup(int p) {
    tr[p].max = max(tr[p << 1].max, tr[p << 1 | 1].max);
}

void lazy(int p, bool st, LL update_val, LL add_val) {
    auto& t = tr[p];
    if (st) {
        t.max = update_val;
        t.add = 0;
        t.update = update_val;
        t.st = true;
    }
    t.max += add_val;
    t.add += add_val;
}

void pushdown(int p) {
    auto& t = tr[p];
    if (t.st || t.add != 0) {
        lazy(p << 1, t.st, t.update, t.add);
        lazy(p << 1 | 1, t.st, t.update, t.add);
        t.st = false;
        t.update = 0;
        t.add = 0;
    }
}

void build(int p, int l, int r, LL a[]) {
    tr[p] = {l, r, a[l], 0, 0, false};
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(p << 1, l, mid, a);
    build(p << 1 | 1, mid + 1, r, a);
    pushup(p);
}

void modify(int p, int x, int y, bool st, LL val) {
    auto& t = tr[p];
    if (x <= t.l && t.r <= y) {
        if (st) {
            lazy(p, true, val, 0);
        } else {
            lazy(p, false, 0, val);
        }
        return;
    }
    pushdown(p);
    int mid = (t.l + t.r) >> 1;
    if (x <= mid) modify(p << 1, x, y, st, val);
    if (y > mid) modify(p << 1 | 1, x, y, st, val);
    pushup(p);
}

LL query(int p, int x, int y) {
    auto& t = tr[p];
    if (x <= t.l && t.r <= y) {
        return t.max;
    }
    pushdown(p);
    int mid = (t.l + t.r) >> 1;
    LL res = -1e18;
    if (x <= mid) res = max(res, query(p << 1, x, y));
    if (y > mid) res = max(res, query(p << 1 | 1, x, y));
    return res;
}

int main() {
    int n, q;
    scanf("%d%d", &n, &q); // 用scanf加速输入
    LL a[N];
    for (int i = 1; i <= n; i++) {
        scanf("%lld", &a[i]);
    }
    build(1, 1, n, a);

    while (q--) {
        int op, l, r;
        scanf("%d%d%d", &op, &l, &r);
        if (op == 1) {
            // 操作1：重置为x
            LL x;
            scanf("%lld", &x);
            modify(1, l, r, true, x);
        } else if (op == 2) {
            // 操作2：加x
            LL x;
            scanf("%lld", &x);
            modify(1, l, r, false, x);
        } else {
            // 操作3：查询最大值
            printf("%lld\n", query(1, l, r));
        }
    }

    return 0;
}

3.4 代码测试与验证

题目输入示例：

复制代码 
6 6
1 1 4 5 1 4
1 1 2 6  // 区间[1,2]重置为6
2 3 4 2  // 区间[3,4]加2
3 1 4    // 查询[1,4]最大值
3 2 3    // 查询[2,3]最大值
1 1 6 -1 // 区间[1,6]重置为-1
3 1 6    // 查询[1,6]最大值

手动计算过程：

  1. 初始数组：[1,1,4,5,1,4]；
  2. 操作 1（重置）后：[6,6,4,5,1,4]；
  3. 操作 2（加 2）后：[6,6,6,7,1,4]；
  4. 查询 [1,4] 最大值：7；
  5. 查询 [2,3] 最大值：6；
  6. 操作 1（重置）后：[-1,-1,-1,-1,-1,-1]；
  7. 查询 [1,6] 最大值：-1；
  8. 输出结果：7、6、-1，与题目示例一致。

四、多区间操作的通用解题框架

通过以上两个例子，我们可以总结出多区间操作的通用解题框架，无论遇到哪种组合，都可以按以下步骤思考：

4.1 步骤 1：确定操作优先级

这是最核心的一步，需明确不同操作的执行顺序。常见优先级规则：

  • 覆盖类操作（如重置）> 算术类操作（如乘、加）；
  • 算术类操作：乘 > 加（避免精度损失）。

4.2 步骤 2：设计结构体与懒标记

  • 结构体需包含：区间边界、维护的核心信息（和 / 最大值 / 最小值）、每个操作对应的懒标记；
  • 懒标记初始值：不影响原始数据（如乘标记 = 1，加标记 = 0，重置标记 = false）。

4.3 步骤 3：实现核心辅助函数

  1. pushup：根据左右孩子的信息，整合父节点信息（固定逻辑，与单标记一致）；
  2. lazy：根据优先级，更新当前节点的核心信息和懒标记（关键：按优先级顺序更新）；
  3. pushdown：按优先级顺序，将当前节点的懒标记下放给左右孩子，然后清空当前节点标记（关键：顺序与 lazy 函数一致）。

4.4 步骤 4：实现建树、修改、查询

  • 建树：初始化节点信息和懒标记；
  • 修改：完全覆盖则调用 lazy 函数，否则 pushdown 后递归孩子，最后 pushup；
  • 查询：完全覆盖则返回核心信息，否则 pushdown 后递归孩子，整合结果。

五、高频易错点总结

多区间操作的代码复杂度较高，新手容易踩坑，以下是五大高频易错点：

5.1 优先级顺序错误

这是最致命的错误！比如 "先加后乘""先加后重置"，会导致结果错误或精度损失。解决方法：先推导公式，再编写代码，确保 lazy 和 pushdown 的操作顺序一致。

5.2 懒标记未清空

pushdown 后未将当前节点的标记恢复为初始状态，导致标记被重复下放，多次执行同一操作。

5.3 重置标记未清空加法标记

重置操作会覆盖之前的所有状态，若未清空加法标记，后续加法会作用于重置前的数值，导致结果错误。

5.4 数据类型溢出

区间和、最大值等可能超过 int 范围，必须用 long long 存储，避免溢出。

5.5 线段树空间开太小

多区间操作的线段树空间仍需开 4 倍原始数组大小，否则会出现数组越界（尤其是数据量达 1e6 时）。

总结

多个区间操作的核心是懒标记的优先级设计，只要明确操作顺序、推导正确的叠加公式，再遵循通用解题框架，就能轻松实现。本文通过两个经典例题，详细讲解了 "区间乘 + 区间加""区间重置 + 区间加" 的实现逻辑，涵盖了公式推导、结构体设计、核心函数编写、完整代码实现等环节，帮助大家彻底攻克这一进阶难点。

线段树的灵活性在于其可维护的信息种类繁多，而多区间操作是线段树进阶的必经之路。掌握了多懒标记的处理方法，你就能应对算法竞赛中绝大多数区间操作问题。建议大家多刷题、多推导，加深对优先级的理解，真正做到举一反三！

创作不易，如果本文对你有帮助，欢迎点赞、收藏、关注三连～

相关推荐
俩娃妈教编程1 小时前
2025 年 09 月 三级真题（1）--数组清零
c++·算法·gesp真题
AI科技星2 小时前
时空的几何动力学：基于光速螺旋运动公设的速度上限定理求导与全维度验证
人工智能·线性代数·算法·机器学习·平面
㓗冽2 小时前
进制转换（字符串）-基础题82th + 表达式求值（字符串）-基础题83th + 删除字符（字符串）-基础题84th
算法
小范自学编程2 小时前
算法训练营 Day31 - 贪心算法 Part05
算法·贪心算法
锅包一切2 小时前
PART2 双指针
c++·算法·leetcode·力扣·双指针
tankeven2 小时前
HJ91 走方格的方案数
c++·算法
俩娃妈教编程2 小时前
2024 年 09 月 二级真题（2）--小杨的矩阵
c++·算法·gesp真题
浅念-2 小时前
C++ STL vector
java·开发语言·c++·经验分享·笔记·学习·算法
小雨中_2 小时前
2.8 策略梯度（Policy Gradient）算法 与 Actor-critic算法
人工智能·python·深度学习·算法·机器学习
热门推荐
01GitHub 镜像站点02从零搭建一个 PHP 登录注册系统（含完整源码）03使用 1panel面板 部署 php网站04openClaw安装飞书插件｜核心踩坑：spawn EINVAL 错误终极解决指南05AI Agent 平台横评：ZeroClaw vs OpenClaw vs Nanobot06MIUI显示/隐藏5G开关的方法，信号弱时开启手机Wifi通话方法07让你的代码更整洁：10 个必知的 Kotlin 扩展函数08Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services09如何解决 OpenClaw “Pairing required” 报错：两种官方解决方案详解10openclaw 配置飞书 报错 应用未建立长连接