【题】每日一题

云深处@2026-02-19 13:34

一.零的数列

描述

请考虑一个由 1 到 N 的数字组成的递增数列：1,2,3,...,N。

现在请在数列中插入 + 表示加，或者 - 表示减，（空格）表示空白（例如 1-2 3 就等于 1-23），来将每一对数字组合在一起（请不要在第一个数字前插入符号）。

计算该表达式的结果并判断其值是否为 0。请你写一个程序找出所有产生和为零的长度为N的数列。

样例

思路

观察到输入一个数字N时，得到的数列有7个数字6个符号（可使用char数组存储符号），且数字递增。每一组数据的整数不变，变的只有符号，因此返回时可以使用string类型

考虑极端情况下，每个符号都是空格（" "），则有输出：1 2 3 4 5 6 7，于是返回的sum是1234567，注意到12 = 1+2*10，123 = 12+3*10，于是可用深度优先遍历解决。

dfs传入的参数需要有：int整数（从1开始递增），该条件下的number，符号，sum值

递归出口：当int整数为N，如果sum==0，使用string类型输出结果

代码

cpp 复制代码

using namespace std;
char op[10];
int N;
void dfs(int pos, int num, int sign, int sum)
{
	if (pos == N)
	{
		sum += num * sign;
		if (sum == 0)
		{
			string s = "1";
			for (int i = 1; i < N; i++)
			{
				s += op[i];
				s += to_string(i+1);
			}
			cout << s << endl;
		}
		return;
	}
	//空格
	op[pos] = ' ';
	dfs(pos + 1, num * 10 + (pos + 1), sign, sum);
	//加号
	op[pos] = '+';
	dfs(pos + 1, pos + 1, 1, sum + num * sign);
	//减号
	op[pos] = '-';
	dfs(pos + 1, pos + 1, -1, sum + num * sign);
}
int main()
{
	cin >> N;
	dfs(1, 1, 1, 0);
}

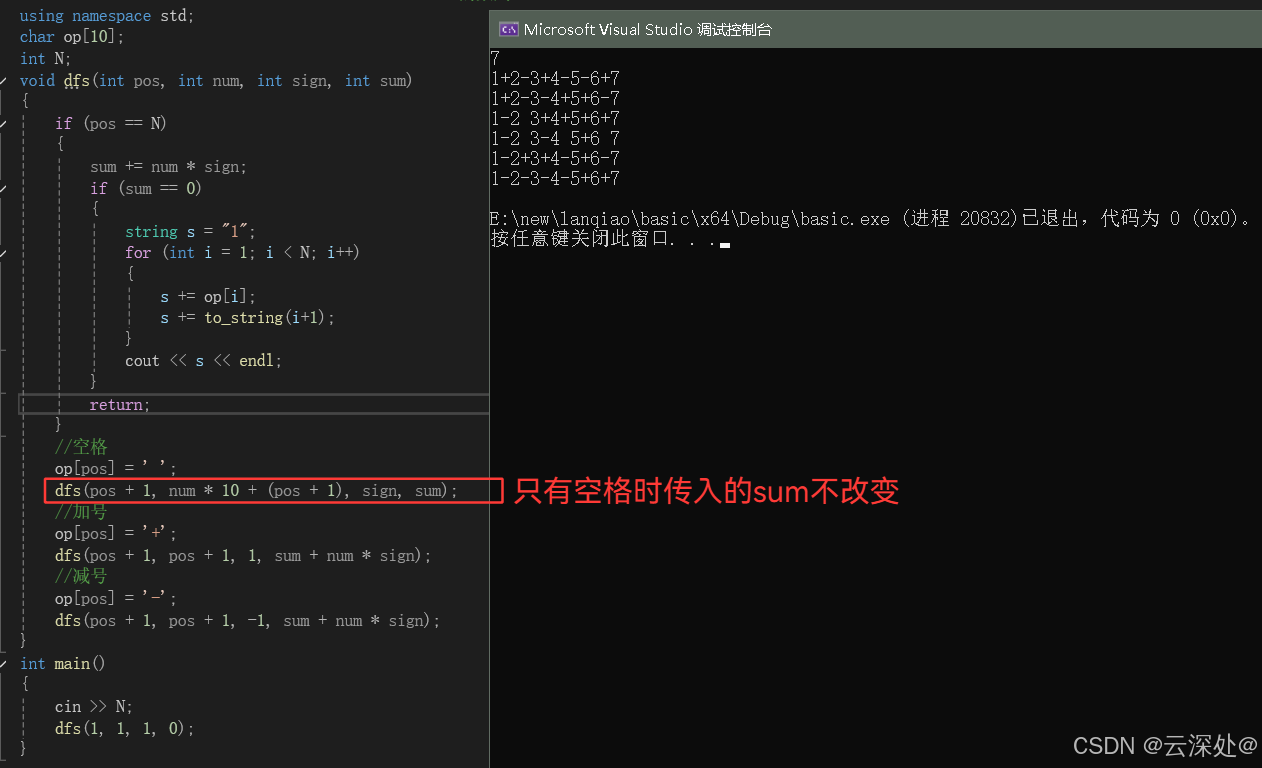
注意：空格递归时传入的sign，一层递归结束时保留原有的sign