之前学习了一些树上问题的知识点,在此做一个小总结。
直径
题目
给定一棵 n 个结点的树,树没有边权。请求出树的直径是多少,即树上最长的不重复经过一个点的路径长度是多少。
求法
两次DFS
首先,随便找一个点DFS,找与该节点距离最远的点,这个点就是直径的端点之一。再从这个距离最远的点DFS,与该节点距离最远的点就是直径的另一个端点。具体证明见树的直径 - OI Wiki。
代码
cpp
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n,maxn,d[100500];
vector<ll>v[100500];
void dfs(ll x,ll fa,ll de){
d[x]=de;
if(d[x]>d[maxn])maxn=x;
for(int i=0;i<v[x].size();i++){
if(v[x][i]==fa)continue;
dfs(v[x][i],x,de+1);
}
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
ll x,y;
cin>>x>>y;
v[x].push_back(y);
v[y].push_back(x);
}
dfs(1,0,0);
dfs(maxn,0,0);
cout<<d[maxn];
return 0;
}DP1
这是一个用两个数组的方法。一个表示从这个点往下最长的路径,另一个表示从这个点往下次长的路径。使用DFS,当一个分支遍历完后,便将该节点的DP值更新,然后找所有节点中最长+次长合起来最长的路径就是直径了。
代码
cpp
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n,maxn,dp1[100500],dp2[100500];
vector<ll>v[100500];
void dfs(ll x,ll fa){
for(int i=0;i<v[x].size();i++){
ll y=v[x][i];
if(y==fa)continue;
dfs(y,x);
ll t=dp1[y]+1;
if(t>dp1[x]){
dp2[x]=dp1[x];
dp1[x]=t;
}else if(t>dp2[x])dp2[x]=t;
}
maxn=max(maxn,dp1[x]+dp2[x]);
}
int main(){
cin>>n;
for(int i=1;i<n;i++){
ll x,y;
cin>>x>>y;
v[x].push_back(y);
v[y].push_back(x);
}
dfs(1,0);
cout<<maxn;
return 0;
}DP2
这种方法只需要一个数组。这种算法在线查询,使用DFS。DP[i]表示当前从i往下最长的一条路径。当遍历完一条分支后,就可以将这条分支最长的路径+1与当前最长路径相加与当前"直径"作对比,再更新dp[i]即可。
代码
cpp
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n,maxn,dp[100500];
vector<ll>v[100500];
void dfs(ll x,ll fa){
for(int i=0;i<v[x].size();i++){
ll y=v[x][i];
if(y==fa)continue;
dfs(y,x);
maxn=max(maxn,dp[x]+dp[y]+1);
dp[x]=max(dp[x],dp[y]+1);
}
}
int main(){
cin>>n;
for(int i=1;i<n;i++){
ll x,y;
cin>>x>>y;
v[x].push_back(y);
v[y].push_back(x);
}
dfs(1,0);
cout<<maxn;
return 0;
}中心
题目
树的中心定义为:一个节点作为整棵树的根节点时,深度最大的节点的深度最小,则该节点是树的中心。
注意,树的中心不一定唯一。
给定一棵 n 个节点的树,求树的所有中心。
求法
首先,我们要知道中心的几个性质:
- 树的中心不一定唯一,但最多有 2
 个,且这两个中心是相邻的.
个,且这两个中心是相邻的. - 树的中心一定位于树的直径上.
- 当树的中心为根节点时,其到达直径端点的两条链分别为最长链和次长链.
(借用树的中心 - OI Wiki,谢谢)
这样子的话,找中心就变得非常简单了。我们只需要再找到直径之后再遍历一遍,找到其中靠中间的一个或两个节点(长度奇数为1个,偶数为2个),就找到中心了。
代码这里就先不贴了。
重心
题目1
给定一棵无根树,求这棵树的重心(可能有多个)。
计算以无根树每个点为根节点时的最大子树大小,这个值最小的点称为无根树的重心。
求法
这里讲解2种求法。
DFS
随机设一个点为根,先将所有节点数统计一下,然后开始DFS。让我们想象一下,假设我们遍历到了一个点,以这个点为根,那么他会有哪些子树呢?肯定会有原来的那些子树,但不要忘了还有一个子树------即在原来的树中,除去自己和自己的子树之外的其他节点构成的树。这个时候再求重心就十分明了了:先将自己的子树都遍历一遍,统计所有子树的节点数之和,并且找到所有子树节点数最大的一个统计下来,然后从所有子树节点数的最大值和整棵树节点的总值减去该点加上所有子树的节点数之和之中取一个最大值,最后看看所有节点谁的最大值最小,他就是这棵树的重心。
代码
cpp
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n,maxn,son[1000500],mmin=0x3f3f3f3f3f3f,m[1000500];
vector<ll>v[1000500];
void dfs(ll x,ll fa){
ll mmax=0;
son[x]=1;
for(int i=0;i<v[x].size();i++){
ll y=v[x][i];
if(y==fa)continue;
dfs(y,x);
mmax=max(son[y],mmax);
son[x]+=son[y];
}
mmax=max(mmax,n-son[x]);
m[x]=mmax;
mmin=min(mmin,mmax);
}
int main(){
cin>>n;
for(int i=1;i<n;i++){
ll x,y;
cin>>x>>y;
v[x].push_back(y);
v[y].push_back(x);
}
dfs(1,0);
for(int i=1;i<=n;i++){
if(m[i]==mmin)cout<<i<<' ';
}
return 0;
}换根DP
重心还有一个等价定义:树中所有结点到某个结点的距离和中,到结点 𝑣 的距离和最小.(借用树的重心 - OI Wiki,谢谢)根据这个,我们就可以进行DP了。
的距离和最小.(借用树的重心 - OI Wiki,谢谢)根据这个,我们就可以进行DP了。
首先我们先选定一个节点为根,进行一遍dfs,将这个节点到所有节点的距离和统计下来,同时将每个节点其本身加上所有子树的节点和也统计下来。接下来进行换根,当从节点u换到它的儿子节点之一的节点v时,除去v和v的子树之外的其他节点的距离都会增加一,而v和v的子树的节点的距离都会减少一,把所有的节点都统计完之后,找到距离和最小的就可以了。
这里就先不给代码了,再下一个题中会给出类似的代码。
题目2
设有一棵二叉树,如图:
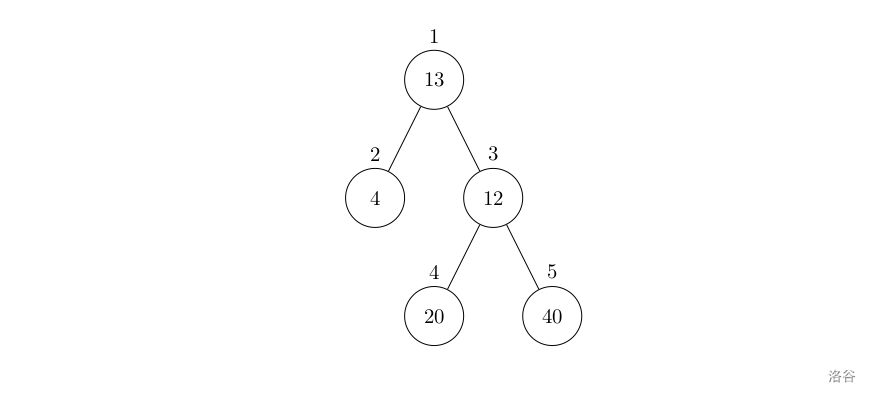
其中,圈中的数字表示结点中居民的人口。圈边上数字表示结点编号,现在要求在某个结点上建立一个医院,使所有居民所走的路程之和为最小,同时约定,相邻接点之间的距离为 1。如上图中,若医院建在 1 处,则距离和 =4+12+2×20+2×40=136;若医院建在 3 处,则距离和 =4×2+13+20+40=81。
输出一个整数,表示最小距离和。
求法
当然了这道题可以用最短路等算法以O(n^2)的时间复杂度通过(毕竟数据范围很小),但还有一种O(n)的做法。
这道题我们我们可以看到最小距离和,好像还是重心。但和刚才的的重心有一点不同:这一个数带上了每个点的权值。这样子的话,我们该怎么求呢?
看上去,DFS的方法好像不行了,那我们来试一下使用换根dp的方法来做吧。首先我们还是选定一个节点为根,进行一遍dfs,将这个节点到所有节点的总距离和统计下来,同时将每个节点其本身加上所有子树的节点人数和也统计下来。接下来进行换根,当从节点u换到它的儿子节点之一的节点v时,除去v和v的子树之外的其他节点的距离都会增加该点的人数,加起来也就是除去v和v的子树之外的其他节点的人数和,而v和v的子树的节点的距离都会减少该点的人数,加起来也就是v和v的子树的人数和。把所有的节点都统计完之后,找到距离和最小的就可以了。
代码
cpp
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n,maxn,son[1000500],minn=0x3f3f3f3f3f3f,uu[1000500],sum,f[1000500],ans[1000500];
vector<ll>v[1000500];
void dfs(ll x,ll fa){
for(int i=0;i<v[x].size();i++){
ll y=v[x][i];
if(y==fa)continue;
ans[y]=ans[x]+son[1]-son[y]-son[y];
dfs(y,x);
}
minn=min(minn,ans[x]);
}
void dfs1(ll x,ll fa){
son[x]=uu[x];
for(int i=0;i<v[x].size();i++){
ll y=v[x][i];
if(y==fa)continue;
dfs1(y,x);
son[x]+=son[y];
f[x]+=f[y]+son[y];
}
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
ll u,x,y;
cin>>u>>x>>y;
uu[i]=u;
if(x)v[i].push_back(x),v[x].push_back(i);
if(y)v[i].push_back(y),v[y].push_back(i);
sum+=u;
}
dfs1(1,0);
ans[1]=f[1];
dfs(1,0);
cout<<minn;
return 0;
}如果大家有其他想法的,可以补充。